跳幅度为-1 模式下的公司债券定价及最佳违约边界
李慧敏, 林建伟
(1- 莆田学院数学与金融学院,莆田 351100;2- 莆田学院金融数学福建省高校重点实验室,莆田 351100)
1 引言
股权和债券定价的合理性会直接影响公司的资产结构及其经营效率,1974 年Merton[1]第一次利用Black 和Scholes[2]提出的期权定价思想来解决公司债券定价的问题,但他提出的建立结构化方法对公司债券定价模型中存在信用利差估计偏低问题.之后Black 和Cox[3]对Merton 模型中公司只有在到期日违约这一假设条件进行放松,建立了首次通过时间模型的公司债券定价方法;Jones 等[4]基于Merton 模型研究了付息票公司债券的定价问题;Zhou[5]考虑了合约到期之前资不抵债时发生违约的情况,在跳扩散模型下利用结构化方法来研究有限到期日公司债券的定价问题;Chen 和Kou[6]则是利用随机分析的方法,考虑双指数跳情况下对永久公司债券进行定价;林建伟[7]利用了最优停时方法对具有一般跳幅度的永久公司债券进行定价.他们的研究工作推广和改进了Merton 模型,具有重要的意义.然而,他们都是考虑违约等于清算而没有考虑资产重组的可能,即一旦公司宣布违约,该公司马上停止运行,公司的股票将一文不值,而债券的价值等于公司在违约时刻的资产价值减去一部份清算费用.显然这些学者所考虑的这些模型不适用于一些不想直接被清算的实际市场,即公司债权人和股东一般不会直接选择清算,而会想让公司继续运营,希望通过重组使得公司解决暂时面临的困难及规避由直接清算而产生的一定比例的清算费用.认识到这一情况,一些学者通过构建违约后进行资产重组的数学模型,即在宣布违约后,将在债权人和股东之间重新分配公司所获得的总价值,在此基础上对公司相关债券进行定价,如Anderson 和Sundaresan[8]提出了利用策略债务支付进行重组的策略,并对具有有限到期日的公司债券的相关定价采用了展开型博弈规则和二叉树方法进行研究和定价,但文章对违约后进行资产重组过程不是用系统的数学模型来描述.随后,Fan 和Sundaresan[9]首次通过给出最佳违约边界选取的标准,限定观察期门槛,选定谈判的策略和明确违约的价值等四个方面对违约后资产重组的过程用系统的数学模型来描述,并在不考虑谈判的时间期限和谈判的费用的情况下,讨论了永久公司的债券定价模式;Francois 和Morellec[10]在文献[9]所提出模型的基础上,对给定谈判时间期限条件下的永久公司债券定价问题采用随机分析及概率论的方法进行定价;林建伟[11]在含有违约观察期过程的公司债券定价模型中利用纳什均衡原理和巴黎型期权定价思想进行定价.这些学者的研究具有重要的意义,但他们依旧没有考虑具有有限到期日这个限制条件下公司债券的定价问题,均只考虑稳态情形,而没有考虑存在本质困难的限定到期日的公司债券相关定价问题.Broadie 和Kaya[12]在文献[10]的框架上给出了利用参数函数来描述最佳违约边界的假定,给出了公司债券相关的二叉树定价格式,从而得到了离散形式的既考虑违约观察期又考虑截止时间有限的公司债券相关的定价形式,但其没有对最佳违约边界进行讨论;接着,Dai 等[13]将Broadie 和Kaya 提出的模型推广到连续的模型上,并利用离散惩罚函数求得了公司债券相关定价的数值解,但他们没有从数学理论去验证最佳违约边界是否存在、是否是唯一的和相关公司价值是否具有单调性,也没有讨论公司在破产保护期内的策略债务支付息票数额大小,只是利用数值计算来研究最佳违约边界曲线的一些性质.以上所述的这些文献均没有考虑公司的资产价值会因为突然发生的不好事件而引发的急剧缩减情况.在实际市场中,投资人会关注公司的资产价值可能由于公司突然暴露出的负面消息导致剧烈“向下跳空”的现象,向下跳空有一个重要特殊情形-假定跳跃幅度为常数-1,即一旦公司资产发生跳跃资产价值瞬间下降为0,公司面临着瞬间破产风险.从数学上看,在跳幅度为-1 的假定条件下公司债券定价的相关问题是一种压力测试下对公司债券和股价的估值,并考虑违约强度对定价的影响.林建伟和李慧敏[14]采用微分方程方法对公司的资产价值变化是依据跳扩散(跳幅度为-1)模型下永久公司债券的相关定价问题和资产的最好结构配置问题进行了研究,给出了显式化的公司资产相关价值(包括股票、债券及总价值)定价、最佳的杠杆比率及违约边界的具体表达式,并通过数值分析,解释跳跃强度变化导致的金融变化现象,但该文章考虑的是稳态情形,而限定到期日的公司债券的相关定价问题显得更为困难.另一方面,在实际金融市场上,一旦公司发生突发事件,对公司造成的影响往往是致命的.因此,本文在具有本质困难的限定到期日的公司债券相关定价问题上综合考虑两种关键的实际市场情况(即公司在违约之后会首先考虑进行资产重组使得公司可以继续经营下去以及如果公司发生突发事件就会导致公司的资产价值急剧缩减这两种情况),使得定价模型更符合实际市场,即本文所要探讨的是在公司资产的相关价值变化过程依据跳扩散(跳幅度为-1)的模式下,采用Fan 和Sundaresan 提出违约后将债券转化为股票的资产重组模式,对违约后进行资产重组及限定到期日的公司债券的相关定价问题采用结构化的方法和最优停时的策略进行研究,并对最佳违约边界存在且唯一这一重要性质给出了理论上的证明,最后通过数值分析研究跳强度对公司债券价值的影响.
2 相关知识
2.1 基本参数和条件的设定
1) 用常数r 表示市场存在套利的机会为零及无风险的利率;
2) 一个公司同时发行了股票E 和具有有限到期日T 且到期本金为P 的公司债券D,约定没有违约的情况下债权人在每单位时间内除了可以得到的息票收益为CP 元外,还可以从公司发行的债券中得到γCP 的税盾收益;股东通过红利取得收益,其中γ(0 <γ <1)表示企业的税率;
3) 在(Ω,F,{Ft}t≥0,P)空间下,公司的资产价值Vt的变化规律遵循跳扩散的模式

其中μ 表示期望的收益率,σ 表示波动率,δ 表示公司总现金支付率,{qt}t≥0表示泊松跳过程(其强度为λ),{Wt}t≥0表示标准布朗运动,且假设泊松过程{qt}t≥0与标准布朗运动{Wt}t≥0之间是相互独立的;
4) 令公司股票的价值取得最大值作为确定最佳违约边界的标准;
5) α(0 <α <1)表示清算的损失率;
6) 违约后资产的重组方式采用的是债券转换为股票的模式[9]:在任一违约时刻τ 时,令Vτ表示此刻公司的资产价值.当公司宣布违约后,公司不进行清算,而是运用将债券转换为股票的方法来重组公司的资产,公司在违约时刻是将公司债券转化为股票从而使公司成为一个全股票的公司并向投资者出售股票的方式来获得资金,通过这种方式将不会因为直接清算而造成公司资产的损失;接着,债权人和股东会采用纳什均衡的原理重新配置违约后公司的资产价值Vτ,从而得到债权人和股东最终各自拥有的最合适比例.
2.2 纳什均衡原理
假设在[t,T]上均有可能宣布违约,令T[t,T]表示发生违约的时刻(即停时);如果公司在[t,T]上没有宣告违约,则规定τ = ∞.设Vτ表示公司在违约时刻τ ∈T[t,T]∪{∞}的资产价值,则当V ≤Vτ时,如果公司没有考虑进行资产重组,则直接被清算.此时股票将没有任何价值,而债券价值将只有(1-α)Vτ;如果公司决定资产重组,那么由上述的假定条件6),违约后公司所获得的总价值Vτ将在债权人与股东之间依据纳什均衡原理重新确定各自所拥有的价值,即债权人和股东在公司宣布违约后将得到的价值分别确定为
E(Vτ)=θVτ, D(Vτ)=(1-θ)Vτ,
其中θ 表示分配给股东比例.利用纳什均衡分配原理可得,最佳分配比例θ*可表示为
θ*=arg max{[θVτ]η[(1-θ)Vτ-(1-α)Vτ]1-η},
即θ*=αη,其中η(0 ≤η ≤1)表示股东谈判的能力.
所以,公司在任意时刻τ 选择了违约之后,公司股票和债券的价值可分别表示成如下式子
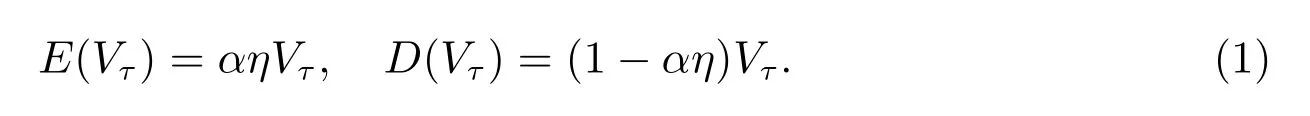
3 公司债券的定价
3.1 股票价值定价模型
根据上述的基本假设及风险中性测度Q,在公司宣布违约的任一时刻(即停时)τ,股票的价值E 的可以用下列模型来描述

其中,等式(2)右边第一个积分项代表了股东通过红利取得收益的贴现值;如果公司在[t,T]这范围内选择违约,则利用第二个式子表示股东在违约后利用重组资产而取得收益的贴现值;如果公司在[t,T]这个范围内不宣布违约,利用第三项表示这种情况下股东获得的贴现值为V -P.

终值条件

边界渐近条件
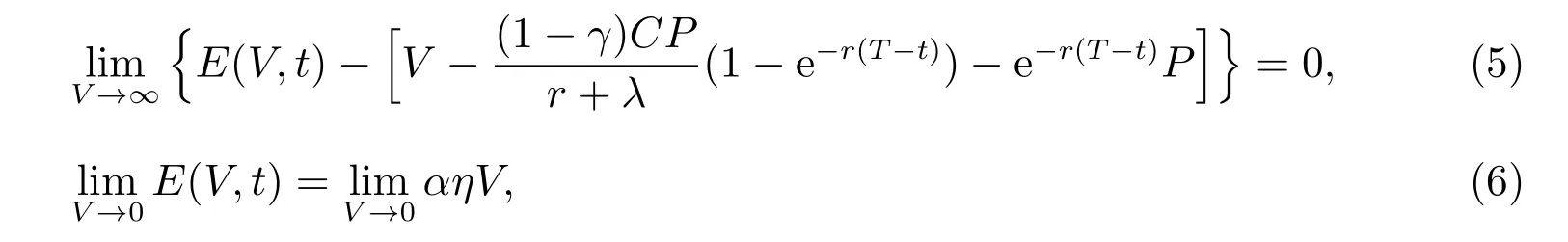

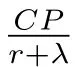
3.2 最佳违约边界的存在及相关性质分析
通过采用偏微分方程中的惩罚函数方法,对于上述股票所满足的变分不等式问题P1,可以证明得出下列结论.
引理1 任意给定时间t,公司的股票价值与股东在违约时刻能够得到的价值之差E(V,t)-αηV,在区域Ω={(V,t)|0 <V <∞,0 ≤t <T}具有单调性,且会随着公司资产价值V 的递增而递增.


进一步构造满足如下性质的光滑化函数Πε(t), t ∈R,

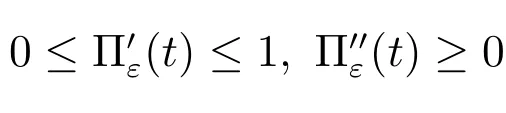
非洛地平缓释片(Ⅱ)对比硝苯地平缓释片控制围绝经期高血压患者血压晨峰现象的临床观察 ………… 刘东升等(21):2976
作变量代换

股票E(V,t)所符合的变分不等式方程问题(3),(4)转化为
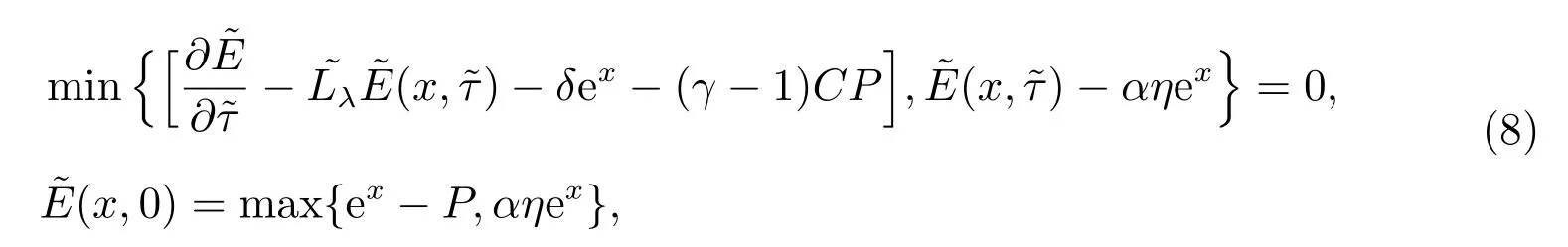
其中
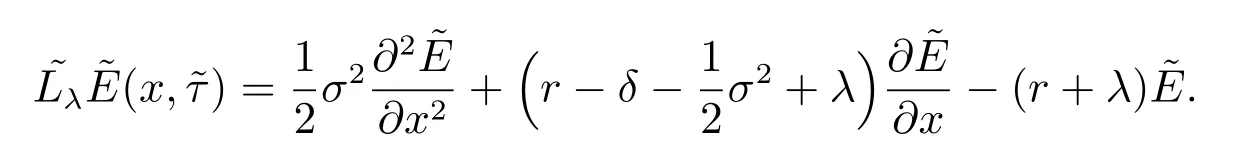
基于上面构造出来的惩罚函数βε(t)和光滑化函数Πε(t)的特点,定义定解问题(8)的相应惩罚问题,表示如下

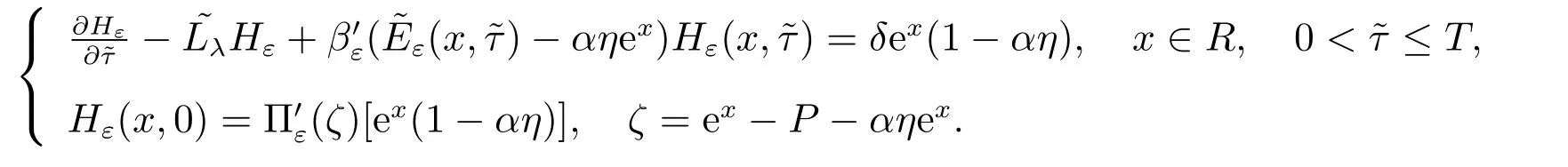
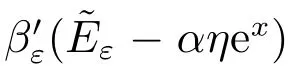
引理2 当(r+λ)≥(1-γ)C 时(该参数条件说明了在任一给定的无风险利率r 条件下,公司从发行公司的债券中获得的税盾收益率γ 越高,则公司能够选择用于付给公司债权人的最大息票率也会越大),股票价值E(V,t)为区域Ω 上时间变量t 的单调递减函数.

其中



定理得证.
对于股票价值E(V,t)与一些相关参数的关系,进一步简要分析如下.
定理3 由(2)所确定的股票价值E(V,t)是关于股东谈判因子η 和清算比例因子α 的单调递增的函数.
证明 根据股票价值E(V,t)满足的最优停时问题(2)可以看出,对于公司任一给定的违约时刻(停时)τ ∈T[t,T]∪{∞},η 越大, E(Vτ)=αηVτ越大,因此相应的股票价值在给定τ 下也越大.由此可得,股票价值E(V,t)是关于股东谈判因子η 的单调递增的函数.同理可证股票价值E(V,t)也是关于清算比例因子α 的单调递增的函数.
3.3 基于最佳违约边界的公司债券定价模型

其中,等式(10)左边第一个式子代表了债权人所拥有息票的收益的贴现值,第二个式子代表公司违约后债权人通过资产的重组得到的收益的贴现值.

其中,(12)式为终值条件,边界条件(13)式说明了债权人在公司宣布违约后能获得(1-αη)V 的收益;而(14)式说明了当公司资产价值趋向于正无穷大时,公司债券可看作和原来有着相同的本金和有限到期日但无风险的公司债券.
4 数值金融分析

图2 和图3 分别说明了公司的股票价值和债券价值随着λ 的变化关系.图2 的数值结果表明,股票的价值会随着跳强度的增大而增大,这是由于在跳扩散(跳幅度为-1)的模型下,公司采取的是让股东能够取得最大权益作为最优的运营策略,而股东为了防止股票变得一文不值,则会通过降低违约风险来提高公司的信用等级,从而使自己所能获得的利益最大化.然而,公司资产有可能瞬间下跌为零,公司债券对市场投资者的吸引度被降低.因此,从图3 的的数值结果可以看出,公司相应的债券价值也将被降低了.

图1 最佳违约边界曲线随λ 的变化情况

图2 股票价值E(V,0)随λ 的变化情况
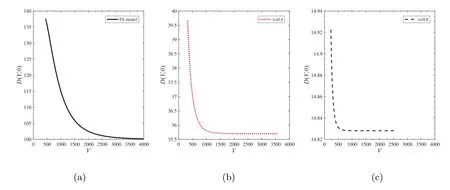
图3 债券价值D(V,0)随λ 的变化情况
5 结束语
根据实际市场中比较可能出现的情况,本文综合考虑了公司的资产价值存在因突发事件瞬间下跌为0 的情况(采用跳扩散(其跳幅度为-1)的模型来描述公司的资产价值变化过程)和采取股票和债券互换作为违约后资产重组的模式,对具有有限到期日公司股票和债券定价问题利用随机分析理论、结构化方法和最优停时方法建立了连续的数学模型,利用偏微分方程中的惩罚函数对最佳违约边界的存在性及唯一性、股票价值的单调性进行了理论上的阐述与证明,同时也对公司股票价值和各参数之间的关系进行了讨论.最后,采用离散的惩罚函数得到最佳违约边界以及对应的股票价值的数值解,同时,债券价值的数值解也通过运用隐式差分格式求得.数值结果表明:基于跳幅度为-1 的跳扩散模型,且在违约后通过将债券换成股票的资产重组模式中,由于公司资产有可能瞬间下跌为零,市场投资者降低了对公司债券的兴趣,因此公司的债券价值减小;而股东可以通过降低违约风险来提升公司信用等级,从而提升股票价格,这表明公司一般都是采用让股东能够取得最大权益作为最优营运策略.

