一个带有季节变化的生产函数模型及其应用

程毛林, 史国军

(苏州科技大学数理学院，苏州 215009)

1 Introduction

The general form of the traditional production function is Y =Af(K,L), in which K and L are the factors of capital and labor input, respectively, is the technological progress level, and Y is the output. The common forms of the production function primarily include the linear production function[1], the Cobb-Douglas production function (C-D production function)[2,3], the constant elasticity of substitution production function (CES production function)[4], the variable elasticity of substitution production function (VES production function)[5], and the Leontief production function[6],among others. The CES production function model is particularly important, and its expression is as follows

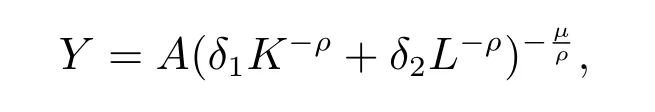
where Y is the output, K is the capital input, and L is the labor input. Additionally,A is the technological progress level and A ＞0, δi(i = 1,2) represents the technically intensive degrees of the factors, respectively, μ represents the homogeneous order or the returns to scale of the function and μ ＞0, and ρ is the substitution parameter and ρ ≥-1. The values of the parameters (A,δi,ρ,μ) are all estimated.

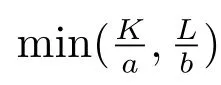
Therefore, most production functions can be considered as special cases of the CES production function, which thus has extensive practicality. The CES production function and the C-D production function are both μ-power homogeneous functions.The output elasticity changes with the changes of the input of production factors. The output Y increases with the increase in the input of production factors,but the increase slows down and approaches a limit value. The change law of the CES production function is obviously consistent with the law of diminishing marginal utility, and meets the conditions of modern economic growth theory[8].

However, in the analysis of economic growth factors, many variables of the data change with the seasons. The traditional CES production function model is not suitable for factors that exhibit seasonal change,and will present large errors,even in modeling.Therefore, this paper proposes a modified CES production function[4,9], and builds a CES production function model that allows for seasonal variations.

The traditional parameter estimation generally uses the linear method for approximate evaluation,but the CES production function model is nonlinear,and would result in a significant error in estimation. Therefore, this paper uses the nonlinear optimization method and adopts the trust-region method[10,11], which is recognized as the most effective algorithm to solve equations with unconstrained optimization problems.

This paper also provides a method to scientifically calculate the contribution rates of input factors to economic growth, allowing for the applicability of the model[12,13].Finally,the paper presents an empirical analysis of the contribution rates of influencing factors to the economic growth of the real estate industry in China by using the modified production function model.

2 The from and parameter estimation of modified model

2.1 The form of modified model

Generally, the form of the CES production function with m input factors is

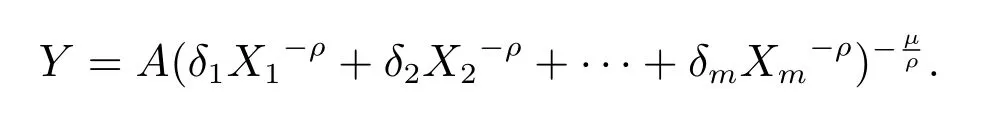
This paper proposes a modified production function model for data with seasonal variations[14]

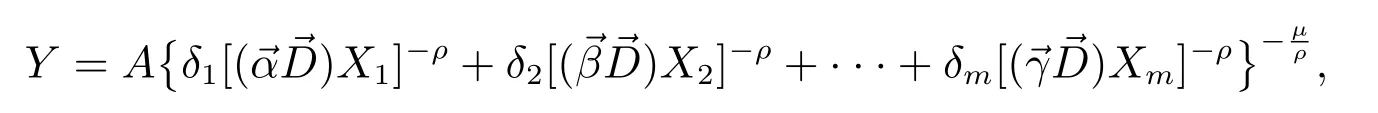
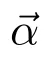
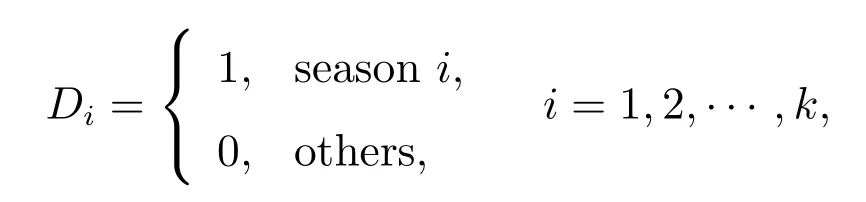
and k generally takes the value of 4 or 12.

It is evident that if α1= α2= ··· = αk= λ1, β1= β2= ··· = βk= λ2, ···, and γ1= γ2= ··· = γk= λm, the model is the general CES production function model,which does not reflect the influence of seasonal variations.

2.2 The parameter estimation of modified model

The modified model of the CES production function is

Y =h(X,η)+ε,

where X =(X1,X2,··· ,Xm),η =(A0,λ,δ1,δ2,··· ,δm,α1,α2,··· ,αk,β1,β2,··· ,βk,··· ,γ1,γ2,··· ,γk,ρ,μ), and ε is the error of fitting of the model.

Let

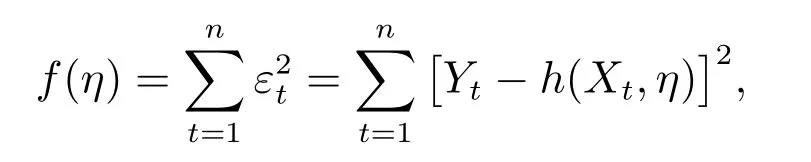
which has the minimum value.

Because function f(η) is complicated and has many parameters, we can use the Matlab software to solve the problem. The research shows that the trust-region method can ensure both a global solution and high precision, as long as the selection of the initial values is appropriate.

3 The calculation method of economic growth factor contribution rate

Suppose the modified production function model with seasonal variations is[14]

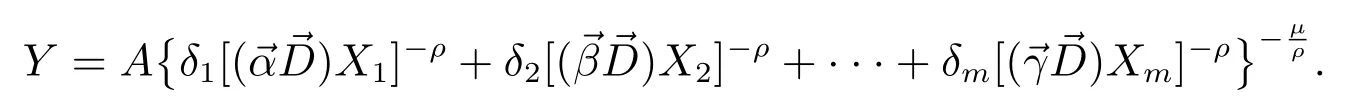
Let

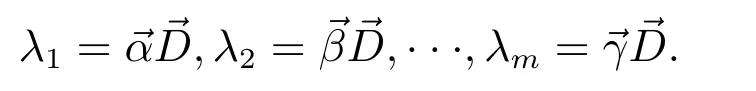
The equation above is therefore

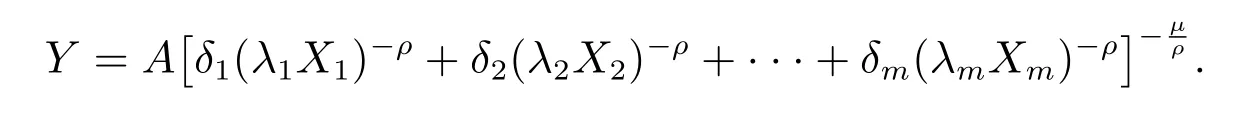
Suppose economic vector (A,X1,X2,···,Xm,Y) changes in the form of curve Γi(t)from period i to period i+1.

In this way,the absolute influence of the value of technological progress to economic growth from period i to period i+1 is

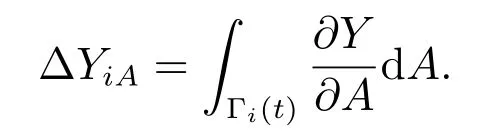
The absolute influence of the value of the jth factor Xjto economic growth from period i to period i+1 is

Then,the contribution rate of factor A to economic growth from period 1 to period n is

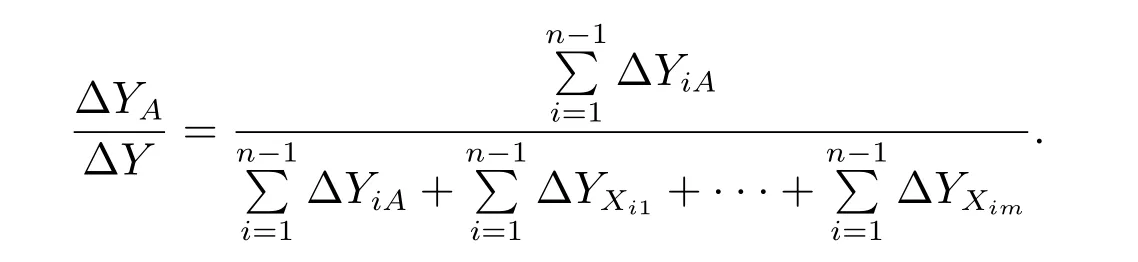
The contribution rate of factor Xjto economic growth from period 1 to period n is

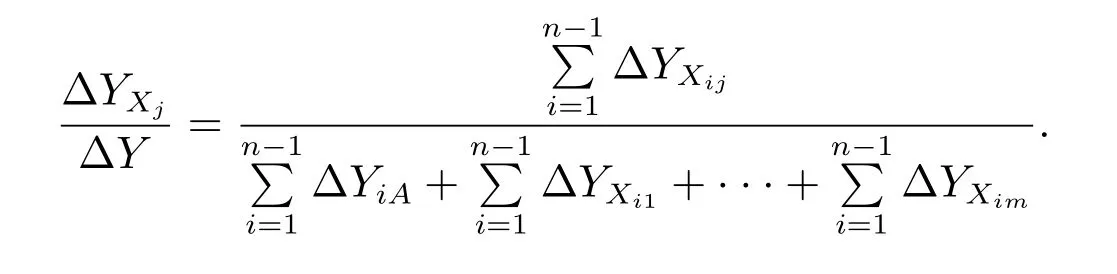
The next section provides a common production function for data with seasonal variations.

更小的像素尺寸通常会引入更多噪点，而更大的像素尺寸能够保证更好的暗光表现，在相同的ISO值下也能够保证更好的画质。因为全画幅传感器的尺寸更大，所以单个像素的尺寸也能够做得更大。

Suppose the modified CES production function with seasonal variations is[14]

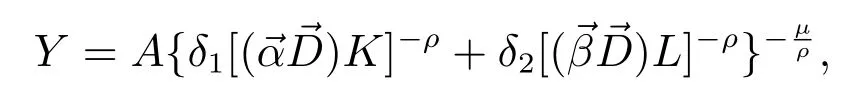
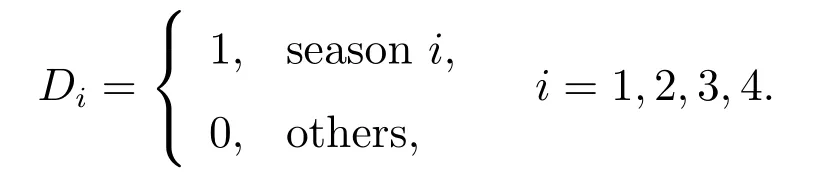
Suppose Γi(t)is the curve that connects point Mi(Yi,Ai,Ki,Li)and point Mi+1(Yi+1,Ai+1,Ki+1,Li+1), and (i=1,2,···,n-1). The equation of this curve is[2,15]

In this way,the value of the influence of factor A on the variation of Y from period 1 to period n is

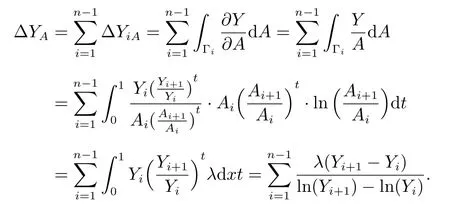
The value of the influence of factor K on the variation of Y from period 1 to period n is

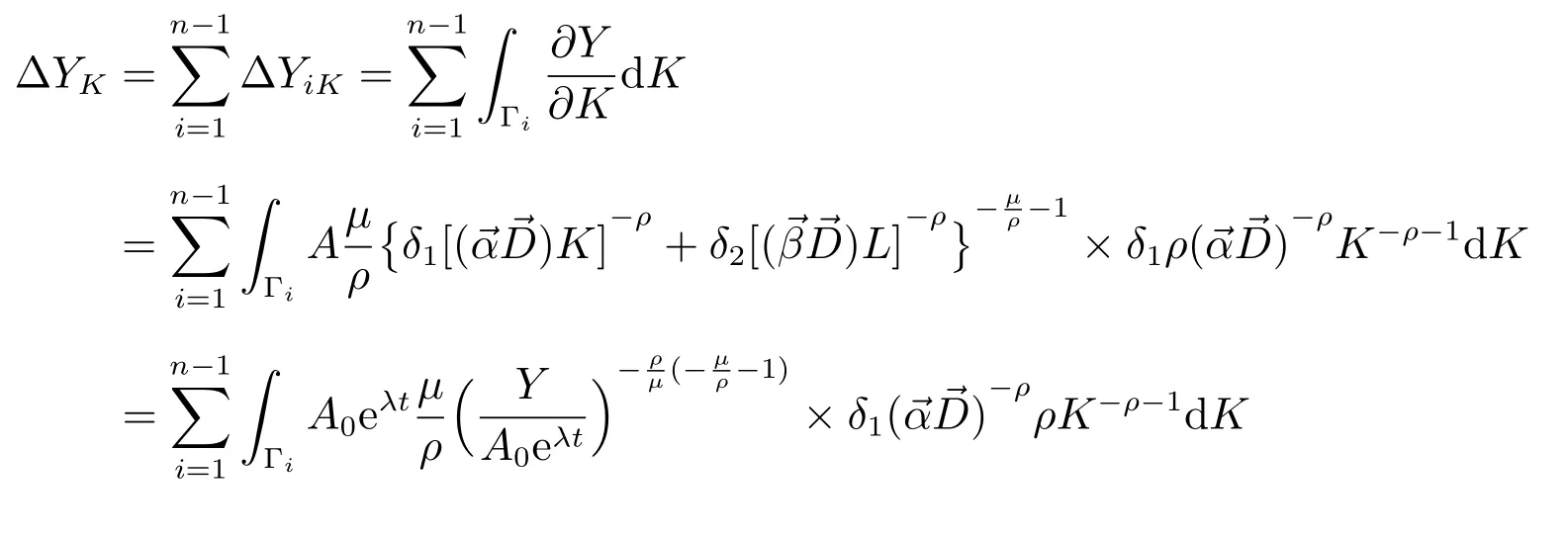
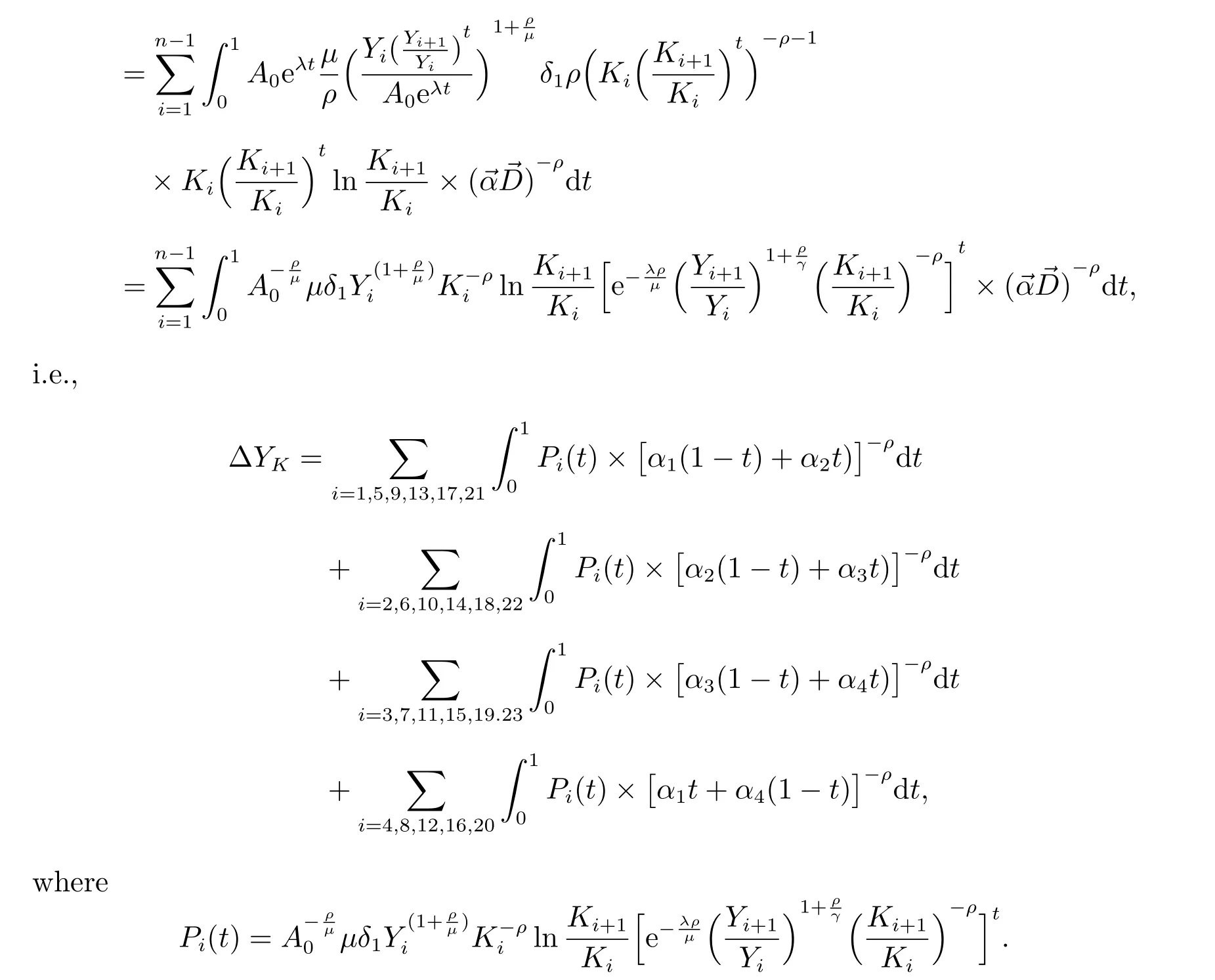
From the numerical integration, we can obtain ΔYK.

i.e.,

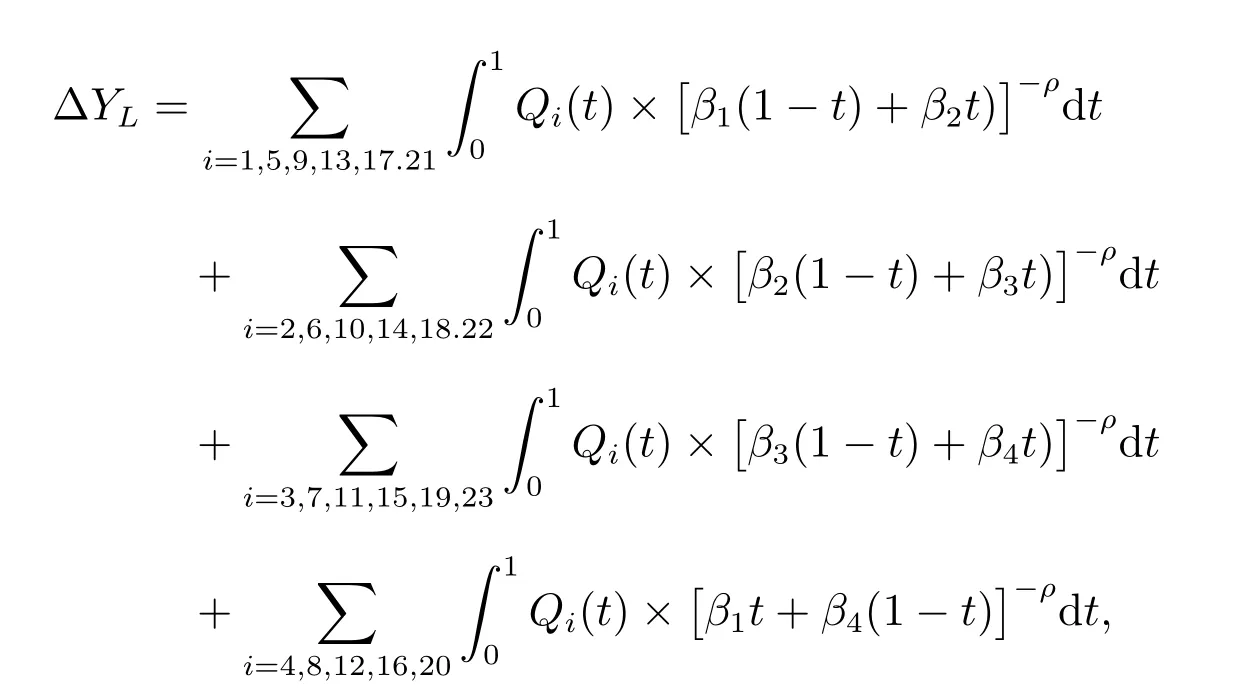
where

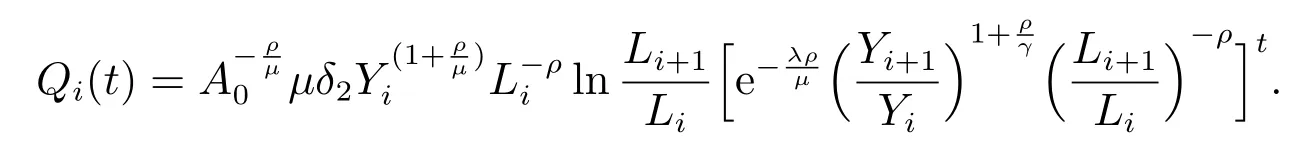
From numerical integration, we can obtain ΔYL.

Then,the contribution rate of factor A to economic growth from period 1 to period n is

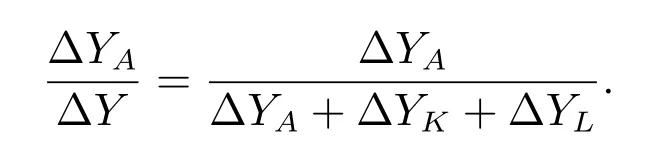
The contribution rate of factor K to economic growth from period 1 to period n is

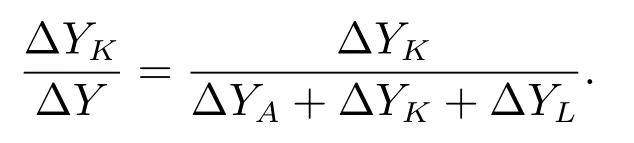
The contribution rate of factor L to economic growth from period 1 to period n is

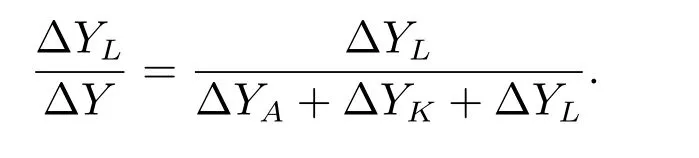
4 Example of application

The real estate industry is a pillar of the national economy, and therefore determining how to scientifically calculate the contribution rate of influencing factors to the economic growth of the real estate industry is currently an important research subject.This section builds a modified CES production function for the related data of the real estate industry that includes seasonal variations, and calculates the contribution rates of influencing factors of the real estate industry to the economic growth of the industry.Table 1 exhibits the related quarterly data of the real estate industry from the years 2011 to 2015. The added value of the real estate industry is recorded as Y (unit: RMB 100 million yuan), the fixed-asset investment of the real estate industry is recorded as K (unit: RMB 100 million yuan), and the number of employees engaging in the real estate industry is recorded as L (unit: 10,000 people). The source of the data is the China Statistical Yearbook.

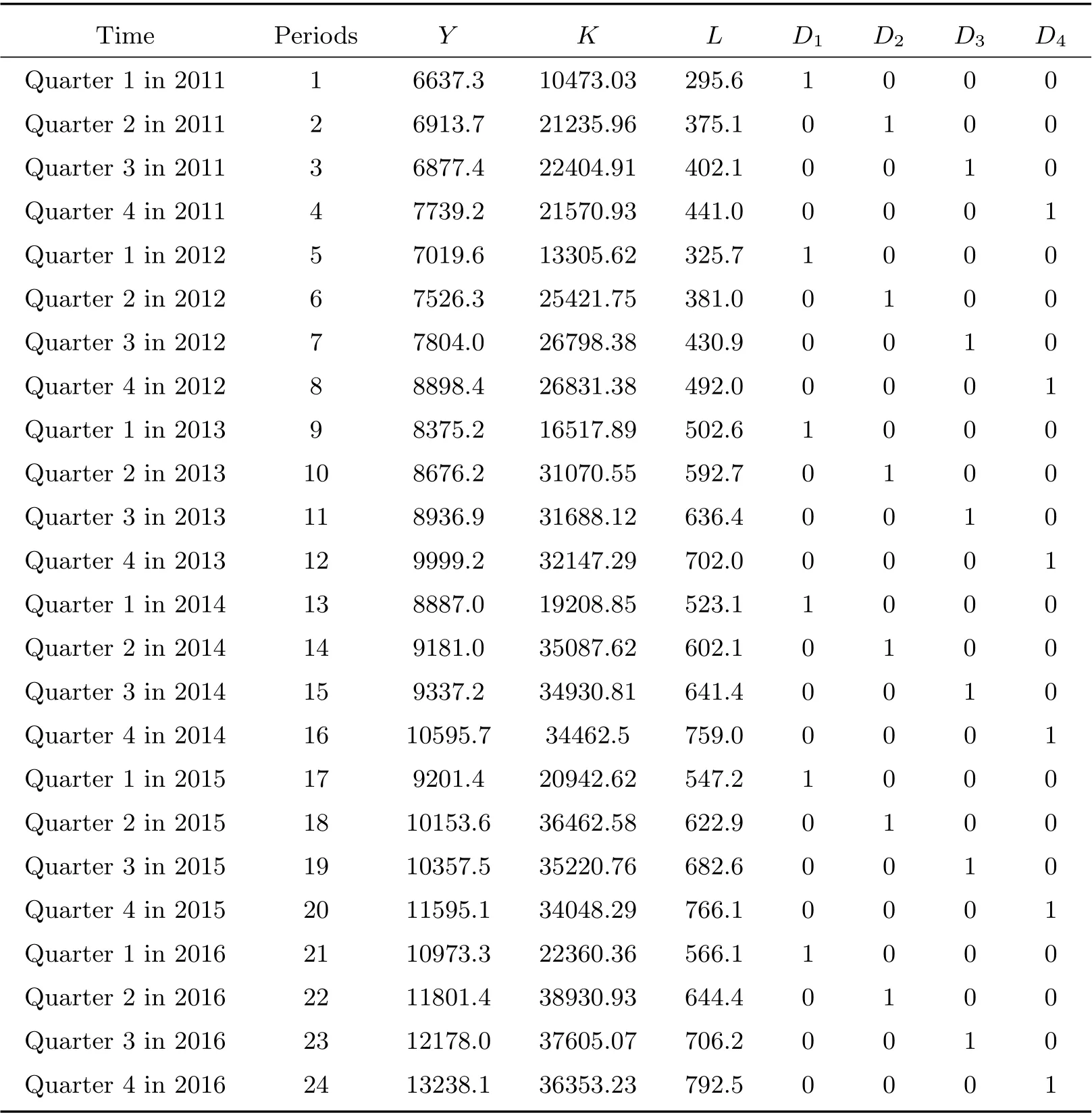
Table 1 Related data of real estate industry in China

Suppose the modified CES production function with seasonal variations is

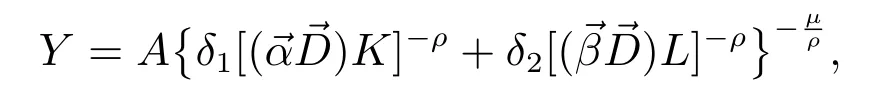
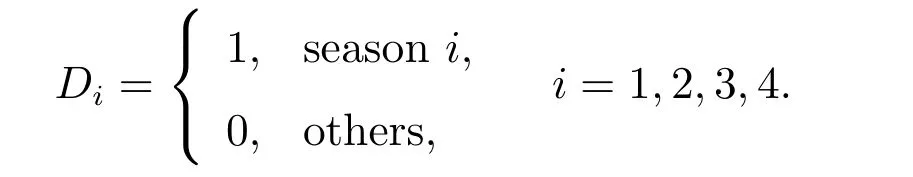
Using the software Matlab2016a and the trust-region method for the parameter estimation of the model results in

η =(A0,λ,δ1,δ2,α1,α2,α3,α4,β1,β2,β3,β4,ρ,μ)

=(2.3655,0.0096,0.2572,0.0074,1.0141,0.6111,0.6266,0.7465,1.1156,0.9357,0.9725,1.0020,0.4099,0.6306),i.e.,

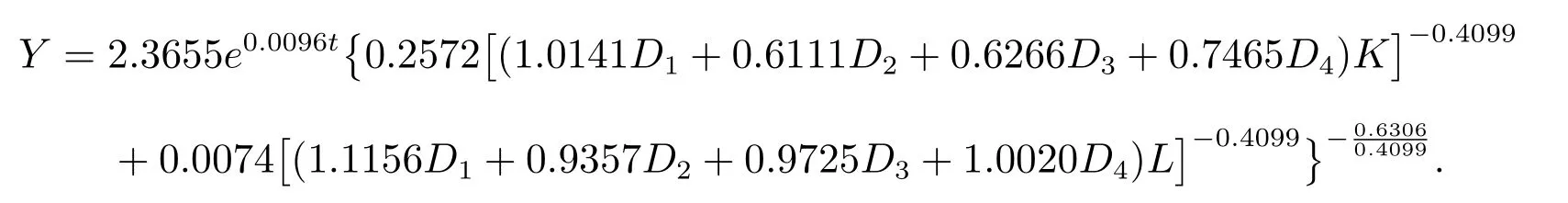
The model’s coefficient of determination

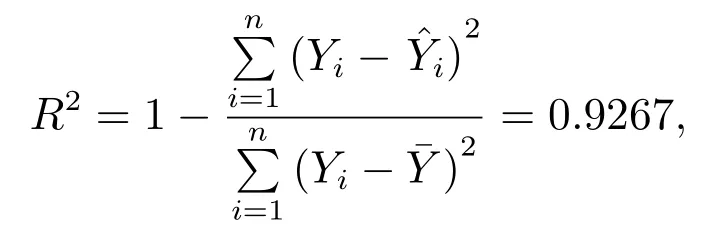
and the mean absolute relative error

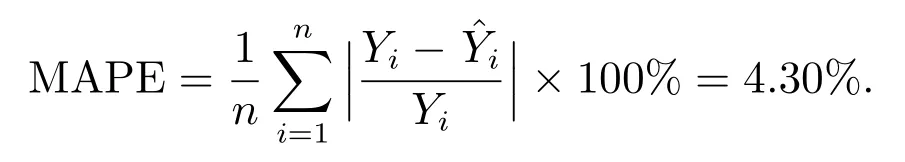
It can be seen that the model exhibits a high fitting precision and a small error.

Additionally, by using the method proposed in this paper, the researcher obtains the following contribution rates of various factors to the economic growth of the real estate industry in China from Quarter 1 of 2011 to Quarter 4 of 2016.

The contribution rate of technological progress (A) to the economic growth of the real estate industry is

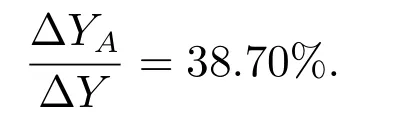
The contribution rate of Factor K to the economic growth of the real estate industry is the following value

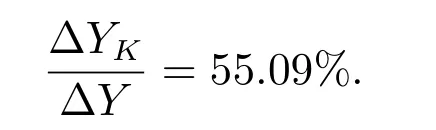
Finally, the contribution rate of Factor L to the economic growth of the real estate industry is

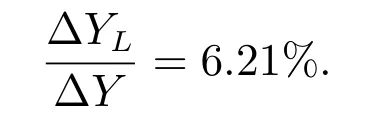
The calculation results indicate that the economic growth of the real estate industry in China mostly depends on capital input,followed by technological progress,and finally labor force. These results are consistent with the reality in China.

5 Conclusion

This paper proposes a modified CES production function model for data with seasonal variations. The paper puts forward a method to scientifically calculate the contribution rates of input factors with seasonal variations to economic growth, and therefore is characterized by practical applicability. Finally, the paper calculates the contribution rates of economic growth factors of the real estate industry in China, and the results are consistent with reality. The proposed method is therefore beneficial for the in-depth study,popularization,and application of production function models,and is significant as a reference for economic decision making.