一种变量是梯形模糊数的两层多随从线性规划模型及其算法
周喜华, 贾洪信, 黄晓红, 邓胜岳, 谢 亮
(1- 广东环境保护工程职业学院基础教育部,佛山 528216; 2- 湖南工业大学理学院,株洲 412007)
1 引言
Zadeh[1]在其发表的论文中首次运用模糊集合的概念,这标志着模糊数学的诞生.康托罗维奇[2]于1939 年,首次提出了线性规划模型及其理论.Zimmermann[3]最早提出模糊线性规划,并通过模糊线性规划对称模型的解法解决了约束模糊型问题.模糊线性规划包含约束模糊型规划、系数模糊型规划及决策变量模糊型规划[4,5].Candler 和Norton[6]于1977 年首先提出“多层规划”模型及其理论,而二层规划是多层规划的基本组成形式,大量应用于两层递阶特征的经济管理系统(利用两层多随处规划对上层为一个领导者、下层为多个随从特征的递阶系统进行建模与仿真).邓胜岳等[7,8]先后研究了系数或决策变量为三角模糊数的二层多随处线性规划模型,给出了可行的算法,并通过算例验证了该算法的可行性和有效性.然而,梯形模糊数是三角模糊数的一般形式,能更好的模拟实际模糊环境,具有更广泛的应用范围.为了拓展模糊二层多随处线性规划模型的应用范围,本文系统研究了一类决策变量为梯形模糊数的两层多随处线性规划模型.因此,本文研究的模型是文献[7]中模型的更一般形式.
2 基础知识
2.1 模糊结构元理论
定义1[9,10]设E 为实数域R 上的模糊集合,而隶属函数记为E(x), x ∈R.如果E(x)满足下述性质:
1) E(0)=1;
2) 在区间[-1,0)上,E(x)是单调递增的函数且右连续,在区间[0,1)上,E(x)是单调递减的函数且左连续;
3) 若x <-1 或x >1 时,E(x)=0,则E 是实数域上的模糊结构元.
定义2[9,10]若模糊结构元E(-x)=E(x),则称E 为对称模糊结构元.
定义3[9,10]若模糊结构元E 满足:
1) x ∈(-1,1), E(x)>0;
2) E(x)连续,且在[-1,0)上严格单调递增,在[0,1)上严格单调递减,则称E 为正则模糊结构元.


则根据E 可得到


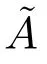
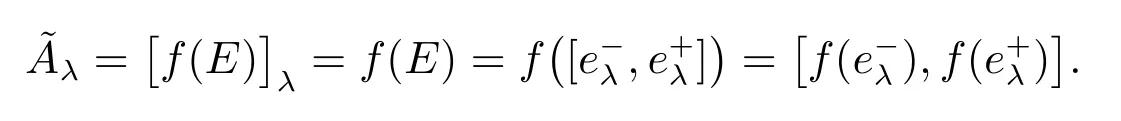
2.2 两层多随从线性规划
两层多随从线性规划模型(MFBLP)及引理
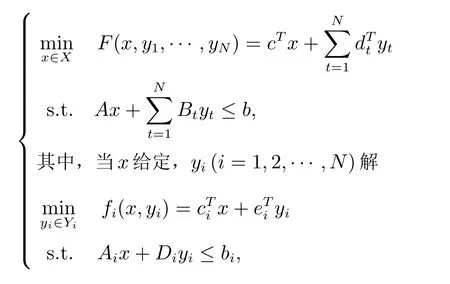

其中i=1,2,··· ,N.
3 一类变量为梯形模糊数的两层多随从线性规划模型及算法
3.1 模型
一类变量为梯形模糊数的二层多随从线性规划模型,具体形式如下




步骤3 根据定理1,将模型(1)的最优解转化为模型(2)的最优解;
步骤4 根据引理5,并利用Matlab 编程运行得到定理1 中模型的最优解;
步骤5 将(2)的最优解代入(1)得到最优解.
4 算例
本节将提供两个算例,其中算例1 为一个领导者一个随从情形,算例2 为一个领导者两个随从情形,并且模型中的决策变量都用梯形模糊数表示.通过两个算例的求解过程验证了本文研究的模型及算法的可行性和有效性.当文中的模型决策变量由梯形模糊数退化为三角模糊数时,算法仍然可行,可见本文的模型是文献[7]中模型的更一般形式.
算例1 考虑上层一个领导者、下层一个随从,且上下层均有约束条件的一类变量为梯形模糊数的两层线性规划问题



步骤2 E(t)为三角模糊结构元,则
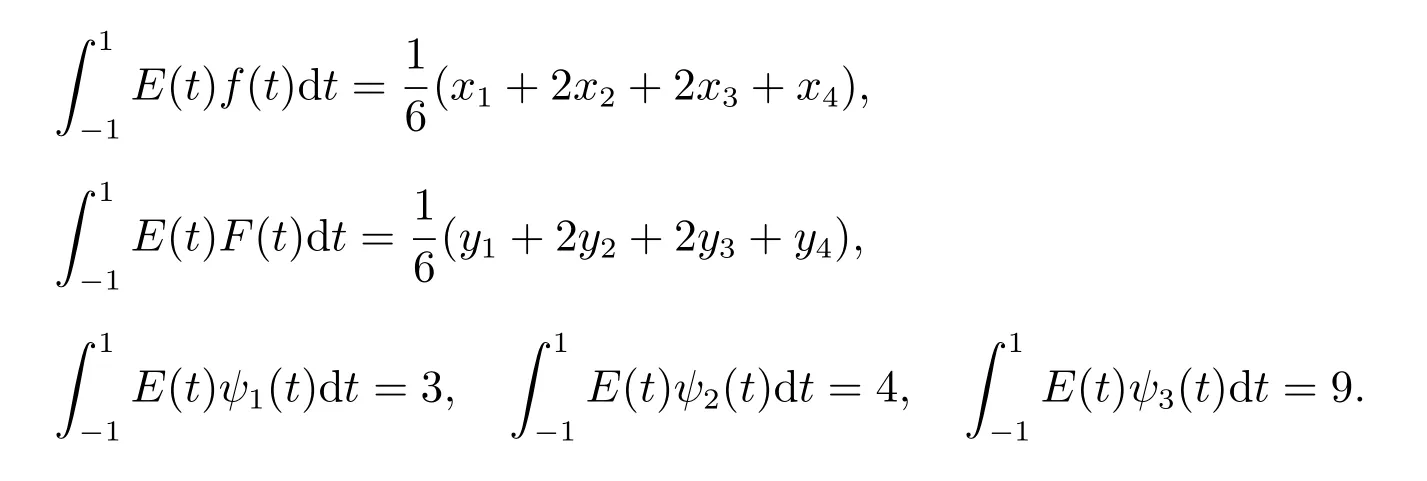
所以可以将原问题(3)转化为下式
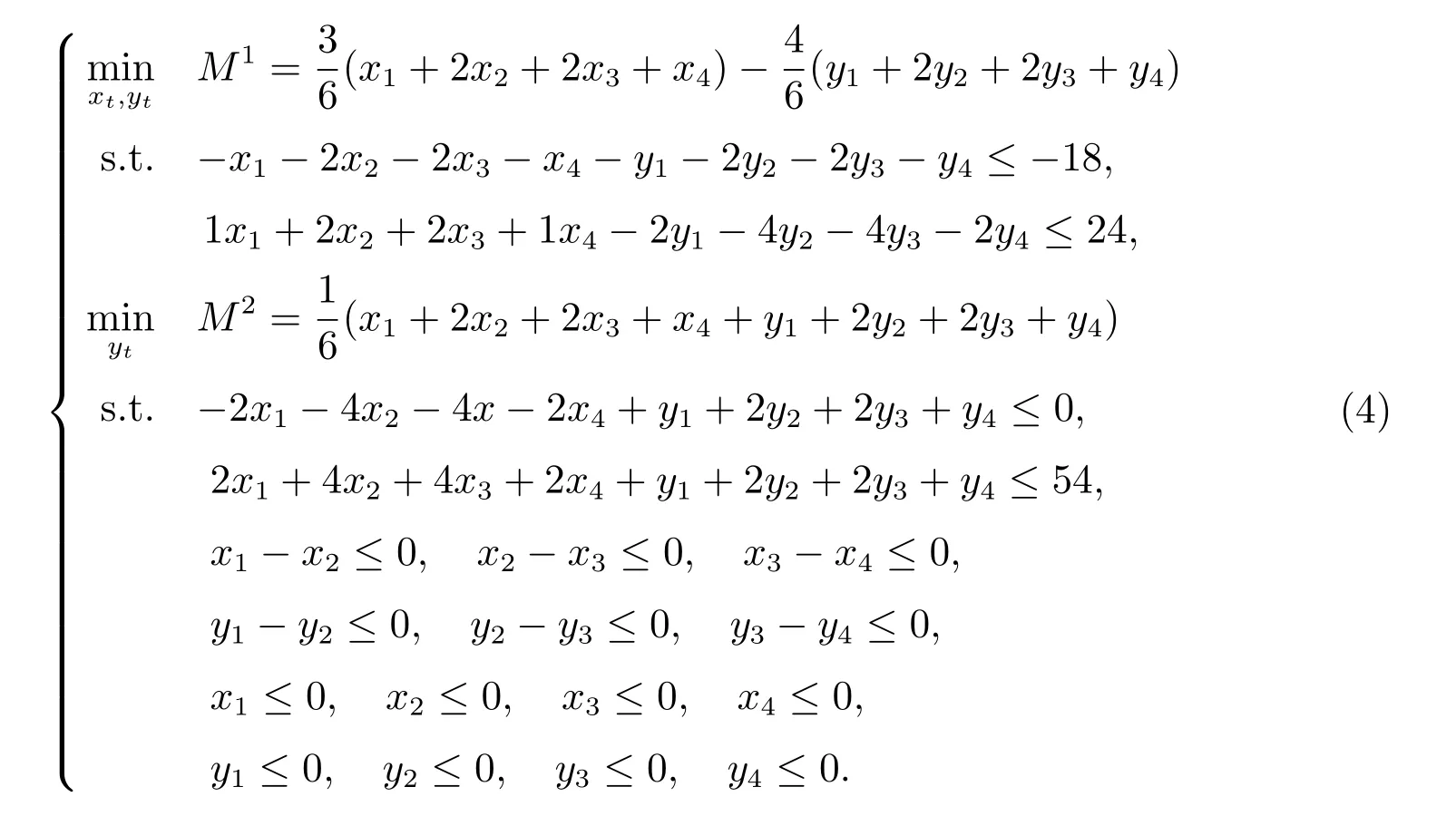
步骤3 由引理5 可知,若存u1, u2, v1, v2, v3, v4, v5∈R,且u1, u2, v1, v2, v3, v4,v5≥0,则有

所以可以得到两种情况:

步骤4 若情况1)成立时,可将问题(4)转化为
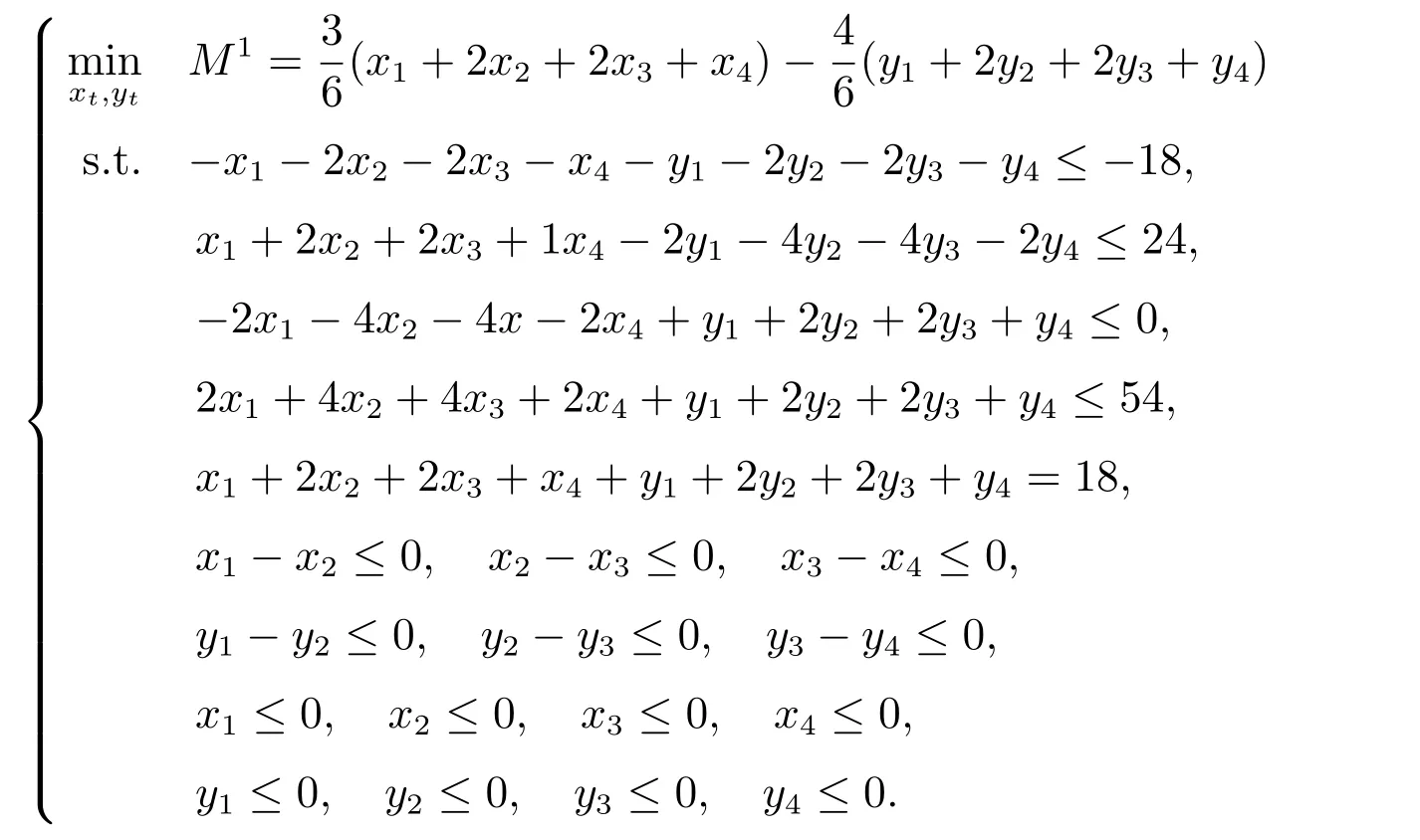
若情况2)成立,则同理可得.
步骤5 情况1)与情况2)所得到的最优值分别为-5.0000, 11.6000,所以情况1)的最优解为问题(4)的最优解,即为x1= 0.1687, x2= 0.2624, x3= 0.5996, x4= 4.1071,y1= 0.5407, y2= 0.9529, y3= 1.9843, y4= 5.5850.将上述结果代入原问题(3)得到:上层问题的最优解为(-10.0187,-6.1384,-3.0244,-1.6567),下层问题的最优解为(0.7094,1.2153,2.5839,9.6921).
算例2 考虑上层一个领导者、下层二个随从,且上下层均有约束条件的一类变量为梯形模糊数的两层多随从线性规划问题




步骤2 E(t)为算法步骤一给出正则三角模糊结构元,则

所以可以将原问题(5) 转化为下

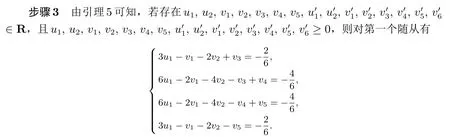

对第二个随从有


步骤4 若情况一成立,可将问题(6)转化为

若情况二、情况三、情况四成立,同理可得.

5 结论
针对一类变量为梯形模糊数的两层多随从线性规划问题,利用模糊结构元的性质,将梯形模糊数进行模糊数的结构元加权序处理,到达了去模糊化的目的,从而使得一类变量为梯形模糊数的两层多随从线性规划转化为两层多随从线性规划,提出了算法,并通过算例验证了该算法的可行性.

