阈值调控的可变服务率流体模型的均衡策略分析
王 硕, 徐秀丽
(燕山大学理学院,秦皇岛 066004)
1 引言
排队在现实生活中随处可见,它们应用于制造业、服务业、金融、财政、保险等各行各业,然而无论哪行哪业建模的初衷就是在提供便利服务的同时获得一定的收益,这引起了各位学者对排队模型展开经济学分析.
Naor[1]最先在排队模型中引入博弈论的观点,提出了顾客在到达系统时会根据一个简单的线性“收益-损失”函数判断是否进入系统.Edelson 和Hilderbrand[2]进一步研究了不可视状态下顾客的止步策略.Wang 等[3]研究了具有N 策略持续重试系统的均衡策略问题.Guo 和Hassin[4]对N 策略排队中的均衡策略及最佳社会策略进行了研究.Dimitrakopoulos 和Burnetas[5]研究了动态服务控制下M/M/1 排队系统中的顾客均衡策略问题.Guo 和Li[6]分析了系统队长不可视情况下的均衡策略.
随着社会科技的快速发展,网络、信息、机械加工制造业以及服务业都面临着大量“顾客”,顾客到达间隔越来越小,到达速率越来越大,离散的顾客越来越接近连续的流体,例如:生产制造业的流水线、网关节的信息传输以及电子信息的流传递等.因而,对流体排队模型进行相关研究就显得尤为重要.Xu 等[7]对M/M/c 工作休假驱动的流体模型展开了稳态分析.Vijayashree 和Anjuka[8]对M/M/1 驱动的工作休假流体排队模型展开了相应研究.徐秀丽等[9]研究了PH/M/1 排队系统驱动的流模型并给出稳态性能指标.当然,也有学者对流体排队模型展开经济学分析.例如:Economou 和Manou[10]对可视情况下具有不同服务状态的流体排队模型中的行为策略进行了分析.
在实际问题中,决策者为了最大限度的利用、维护缓冲器,并不会使其始终以一定速率进行服务,而是根据缓冲器内流体水平的多少适当调整其服务率,使缓冲器的服务率在高低两个状态中来回切换.例如,为防止低流出率下水库水位过高,工作人员会在水位达到某一特定值时开闸放水.这就引出了对具有可变服务率流体模型的研究.进一步,若缓冲器在低速工作状态与高速工作状态的切换遵循某一特定概率,那么当低速工作期缓冲器内的流体水平达到相对多时,如果缓冲器的流出率仍保持在一个较低的速率,这必然会引起缓冲器内的拥挤甚至引发顾客的不满.在此基础上,本文把阈值调控与可变服务率相结合,构建出新的流体模型并给出经济学研究.
2 模型描述
对任意外界随机环境下的流体模型,假设时刻t 流体以速率λ 流入缓冲器,其过程可以看作新顾客的到达.流体流入缓冲器的前提是其净收益为正且其是否流入缓冲器的决定具有不可逆性,即:流入的流体不可中途流出,止步的流体不可临时流入.设X(t)表示时刻t 时缓冲器内的流体水平,I(t)表示时刻t 时的系统状态,用I(t) = 0,1 分别表示低速工作期和高速工作期.阈值调控是指当缓冲器内的流体水平变为0 时,缓冲器进入空闲期,在此期间一旦有流体流入缓冲器,系统立即进入低速工作期,此时系统存在一个较低的流出率μ0, μ0>0,当缓冲器内的流体水平达到事先确定的阈值水平N 时,缓冲器进入高速工作期,此时系统存在一个相对高于μ0的流出率μ1,即μ0<μ1.
此外,需要保证μ0<λ <μ1,否则缓冲器不会满足发生状态转变的条件.例如:当μ0>λ 时,低速工作期间流体水平在0 处达到稳态,即流体一旦流入就会立即通过缓冲器流出,不会存在排队等待的情况,故流体水平不可能达到N;λ >μ1时,若缓冲器处于高速工作期,此时系统的净流入率始终为正,也就是说缓冲器内的流体水平始终以λ-μ1的速率增加,直到达到相应的阈值后保持稳定,所以这种情况下的流体水平不可能下降为0.
综上所述,具有阈值调控的可变服务率流体模型的净输入率可表示为
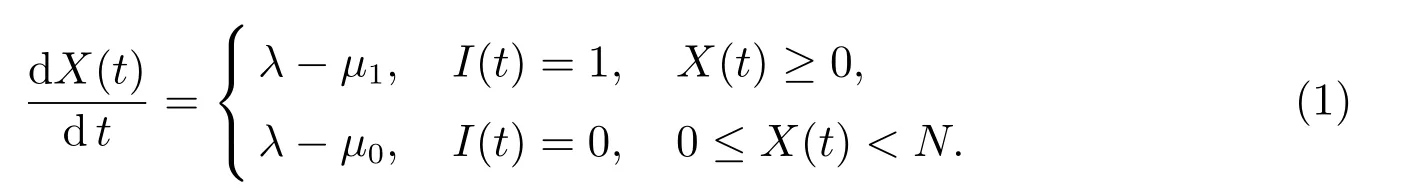
3 完全可视情况下的止步策略分析
假设时刻t 流体到达系统时观察到此时缓冲器的工作状态为I(t) = i, i = 0,1.在此状态下,缓冲器内的流体水平为X(t) = x, x ≥0.用(X(t),I(t)) = (x,i)表示流体到达系统时所观察到的状态.假设流体流出系统时,即流体被服务完时可获得的收益为R.另一方面,流体在缓冲器内的逗留期间,单位时间内又存在着C 个单位的损失.用Gi(x)=R-CSi(x)表示该流体在系统状态为(x,i)时流入缓冲器所获得的净收益,其中Si(x)表示该流体在系统状态为(x,i)条件下流入系统后在缓冲器内的逗留时间,且只有当Gi(x)>0 时流体才选择进入缓冲器排队.
下面考虑两种情况:

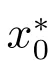


的唯一解,即


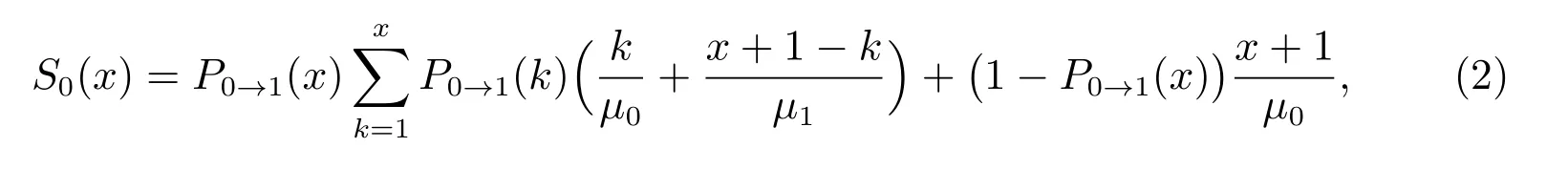
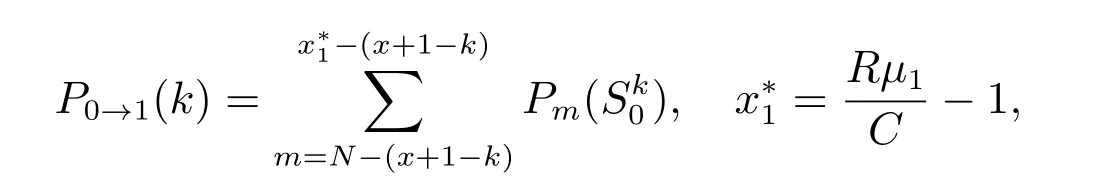

4 单位时间内社会收益
在阈值调控的可变服务率流体模型中,由于缓冲器在状态0 与状态1 之间的转换没有一个固定的概率参数,而是依赖于缓冲器内流体水平的变化情况,所以缓冲器内平均流体水平E(X)的表达较为复杂.因此,本文用Z(x)=μe(G0(x)P0(x)+G1(x)P1(x))表示单位时间内社会收益的效用函数,其中μe表示有效服务率,Pi(X)表示在缓冲器内流体水平为X 的条件下,缓冲器处于状态i 的概率,则有如下定理.
定理2 在完全可视的阈值调控的可变服务率流体模型中,假设某流体到达系统时观察到缓冲器的状态为(x,i),则该流体模型的稳态概率为
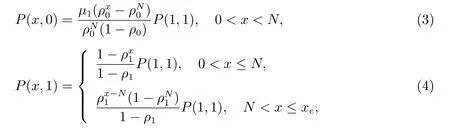
其中


证明 运用文献[11]电子通信网络中有关流体模型的研究方法,把连续时间的流体模型分解为近似的离散排队模型.例如,把一些信息压缩打包使其以数据包或链接的形式进行传输.由此画出该模型在完全可视情况下的状态转移图,如图1 所示.

图1 状态转移图
根据状态转移图可以写出其平衡方程
λP(0,0)=μ1P(1,1)+μ0P(1,0),
(λ+μ0)P(x,0)=λP(x-1,0)+μ0P(x+1,0), x=1,2,··· ,N -2,
(λ+μ0)P(N -1,0)=λP(N -2,0),
λ+μ1)P(1,1)=μ1P(2,1),
1)冬春季清园。冬季清园喷5波美度石硫合剂或1∶1∶200波尔多液;春季萌芽前喷5波美度石硫合剂或1∶0.5∶250波尔多液清园。
(λ+μ1)P(x,1)=λP(x-1,1)+μ1P(x+1,1), x=2,3,··· ,N -1,
(λ+μ1)P(N,1)=λP(N -1,1)+μ1P(N +1,1)+λP(N -1,0),
(λ+μ1)P(N +x,1)=λP(N +x-1,1)+μ1P(N +x+1,1), x=1,2,··· ,xe-N,

由于

即
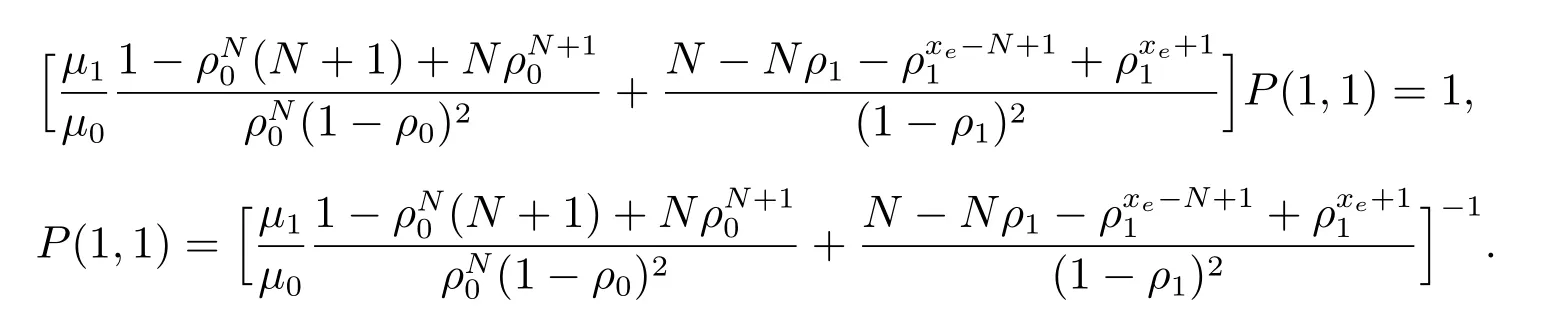
因此,定理2 得证.
定理3 在完全可视情况下的阈值调控的可变服务率流体模型中,假设某流体到达系统时观察到缓冲器的状态为(x,i),则该流体模型单位时间内社会收益的效用函数为
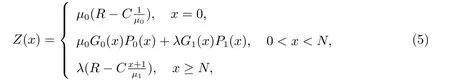
其中
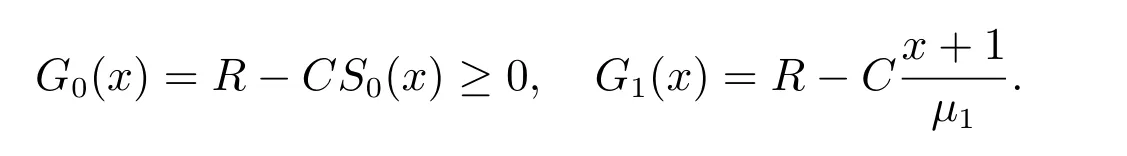
由(2)式可知S0(x).

证明 由定理2 可知
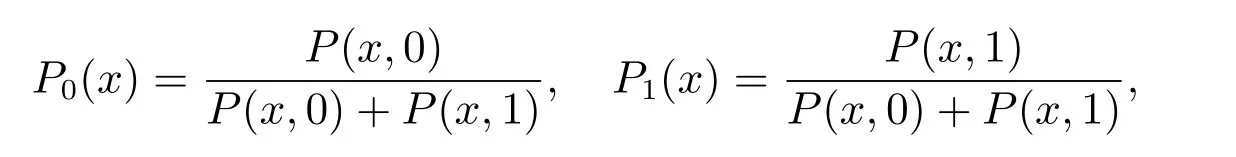
经代数运算可得

因为μ0<λ <μ1,所以当缓冲器处于状态0 时系统的有效服务率为μ0,即μe=μ0;当缓冲器处于状态1 时,系统的有效服务率为λ,即μe=λ.所以有

其中
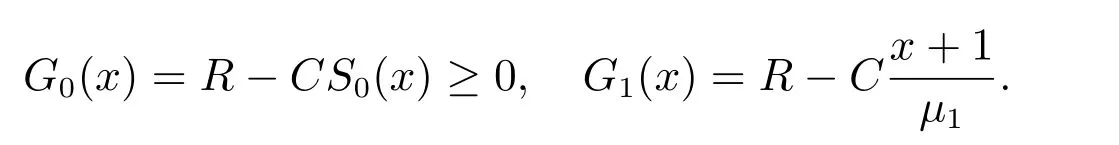
由(2)式可知S0(x).
经代数运算可得到Z(x).因此,定理3 得证.
由于单位时间内社会收益函数的形式复杂性,下面进行直观的数值分析,令μ0=1.2, λ=1.5, μ1=2, R=10, C =1, N =3,4,5,得到图2.
从图2 可以看出,对于固定的参数μ0, λ, μ1, R, C, N,单位时间内社会收益函数因N 的不同而呈现出不同变化;但在x ≥N 部分的函数图像是完全一致的,因为当x ≥N 时单位时间内社会收益函数与N 无关且除了给定的参数只与x 有关.当x = N 时,单位时间内的社会收益达到最大.此外,对于固定参数μ0, λ, μ1, R, C, x,单位时间内社会收益函数随着N 的增大而减小.

图2 单位时间内社会收益随x, N 的变化
5 入场费均衡策略

1) 当缓冲器处于低速工作期时,为了保证缓冲器状态的改变,需保证对任意x, x ∈[0,1,··· ,N)都有G0(x)=R-CS0(x)-p ≥0,即
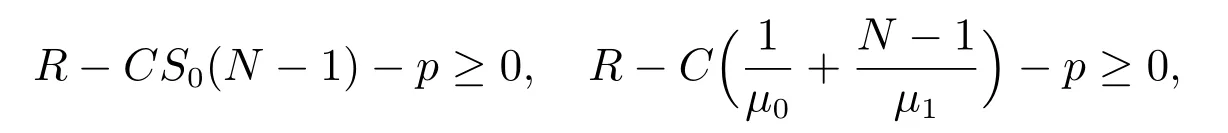
2) 当缓冲器处于高速工作期时,入场费p 需满足
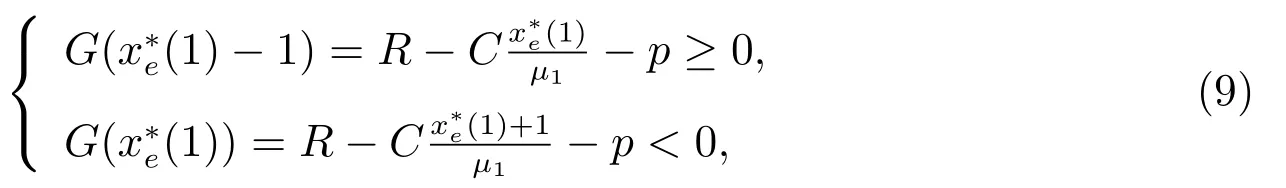
综合上述两种情况,可以得到对决策者而言,最优入场费p*应该满足


因为μ0<μ1,所以

所以得到

即

定理4 假设决策者决定向进入缓冲器排队的流体征收一个入场费p,当流体到达系统时观察到缓冲器的状态为(x,i),则对入场费的征收者而言,其单位时间内的最大总收入可表示为
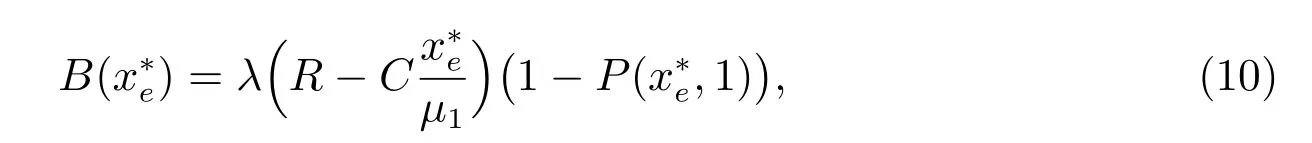
其中
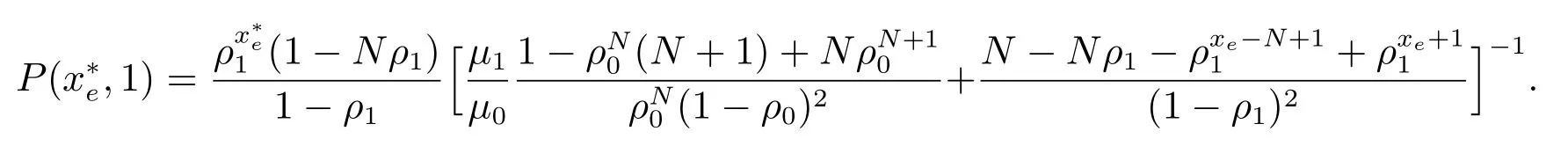
证明 当i=0 时,流体的净收益为
G0(x)=R-CS0(x)-p, x <N-,
当x=N-时

当i=1 时,流体的净收益为



根据定理4 中单位时间内入场费征收者的最大收益,由于其表达式的复杂性,下面给出直观的数值分析,令R=10, C =1, μ0=1, λ=2, μ1=5, N =3,得到图3.
从图3 可直观的看出,单位时间内入场费征收者的最大收益先增大再减小,在x*e=5 处取得最大值.综上所述,如果以社会收益最大化为目标,那么征收一定的入场费是有益的.但是,若入场费的征收者只是为了最大化自己的收益,则他就会向流体征收过高的入场费,从而达不到社会收益最优.

图3 单位时间内入场费征收者的最大收益随的变化

