去奇异化Rankine 源分布面板法自由面数值模拟
韩永浩, 罗志强
(昆明理工大学理学院,昆明 650500)
1 引言
流体力学中的数值模拟被广泛地应用于海洋运输、航天科技和核工程等领域中,二维近水面波与水翼之间的相互作用的数值模拟是近些年来流体水动力学研究的重要课题.通过对二维水下振动体的数值模拟,探索近水面波与水翼之间的相互作用下的振动体周围压力以及自由面波等复杂流场内部机制,对近水面探索器以及水下航行器等的研究具有重大意义.
在过去的几十年中,有大量的数值模拟、理论分析和实验研究的方法研究近水面波与水翼之间的相互作用的问题.Wehausen[1]、Frank[2]利用格林函数数值求解自由面波与水翼相互作用的压力和波高.Lamb[3]建立源面板法,求解自由面非线性波.Vugts[4]计算出自由面摇摆,起伏和滚动圆柱三种情况下的水动力系数.Cao 等[5]运用去奇异化的边界方法求解出三维势流问题.Beck[6]运用时域面板法求解出了浮体在无限深度下波体相互作用下的水动力系数.自由面边界条件对于处理近水域振动体和波之间相互作用的问题时非常重要,如何进行边界条件的处理是当时一大难题.Dawson[7]在1977 年提出了Ranine 源方法,使用Rankine 源法满足辐射和自由面边界条件,用于描述匀速前进的物体的稳定的流动,并获得了成功.Beck 等[8]运用Rankine 源法,把自由面边界积分和圆柱体边界积分两个方程分开表达求解,数值模拟了完全非线性波.由于在自由面的边界积分涉及到无限自由面,Lee[9]将自由面区域截断为有限区域进行积分求解,解决了表面穿透体的非线性辐射问题.Lee[10]考虑孤立源求解完全非线性流体动力问题.Zhang 和Beck[11,12]考虑在有限的自由面区域均匀放置Rankine 源的方法,求解出了二维漂浮物大振幅下的问题.Feng 等[13-16]考虑在自由面Rankine 源稀疏放置,数值模拟了水面圆柱作垂直方向运动的水动力学性态.
综上所述,以上文献考虑各种数值方法数值求解自由面波高与水翼表面压力的水动力学性态.很少文献考虑水下物体作垂直运动时波体之间的水动力学性态.由于自由面波的运动受到水下运动物体和水下源强度的双重影响,很难构建直接关系的表达式,因而给自由面波的求解造成了困难.鉴于此,本文构建了水下圆柱作垂直运动下,在圆柱体和自由面同时放置Rankine 源,巧妙放置Rankine 源的具体位置,使得源的分布符合流体运动的规律,同时巧妙地使用了自由面插值的方法构建自由面波波高与圆柱运动的关系式,求解了源分布下波体运动相互作用的水动力学性态.
本文第2 部分为模型的建立与边界积分方程的推导,第3 部分为边界积分方程的离散与处理,第4 部分为数值实验模拟,最后给出了本文的结论.
2 数学模型以及积分方程的推导
2.1 物理模型
假设在不可压、无粘和无旋的理想流体中,考虑二维无限水深的水面下振动圆柱体水翼,如图图1 所示.当Rankine 源Q 点分布在流体区域V 中,设SQ是以Q 为圆心,ε 为半径的圆的边界.流体区域V 由自由面边界Sf、圆柱体边界Sb、源点Q 所围成的区域边界SQ和无穷远处海底边界围成,其中Sc为平静水面边界,R 为振动圆柱体半径,h 为振动体浸没深度.
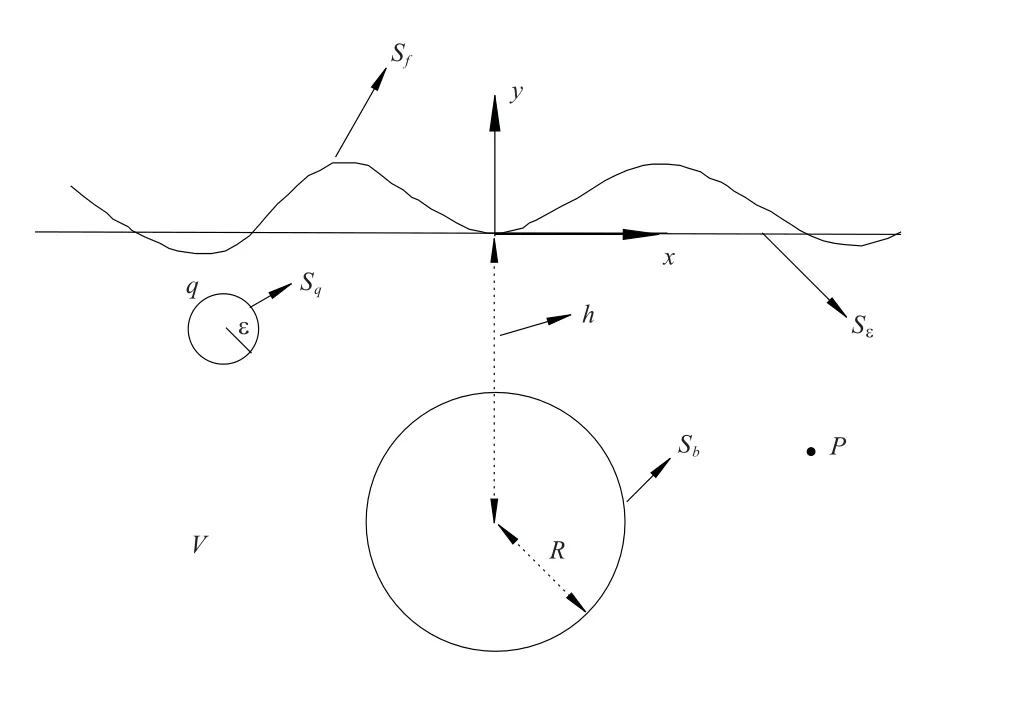
图1 物理模型
圆柱体垂直运动速度为
U =(0,a sin ωt),
其中U 为圆柱体垂直运动速度,a 为振动的振幅,ω 为振动频率.
流体区域内势流φ 满足∇2φ=0.圆柱体与液体的固液边界条件为

其中nB为圆柱体表面外法向量.
自由面运动学边界条件为

其中y =η(x,t)为自由面波高.
自由面动力学边界条件可以表示为

其中g 为重力加速度.
2.2 源分布边界积分方程
设φ 和φ1是流体区域V 的两种速度势函数,分别满足Laplace 方程
∇2φ=0, ∇2φ1=0.
φ 和φ1在流体区域V 中是有限单值函数.对应的速度势关于x 和y 的导数
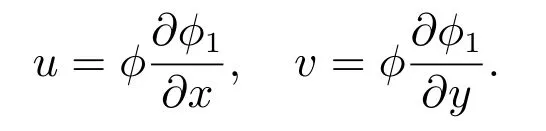
设S 是流体区域V 的所有边界之和,其中l, w 是边界S 上外法向量n 在x, y 正方向上的单位分量,得

由格林公式
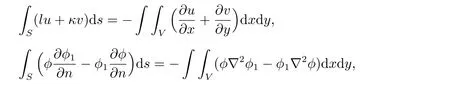
得

取φ1=ln r =ln|P -Q|,其中Q 点是源点,P 点为流体区域V 内部的点.
当源点Q 在流体域V 内部,如图2(a),P 取Q 点处时ln r 无限大,积分区域为V -VQ.流体区域V 的边界为
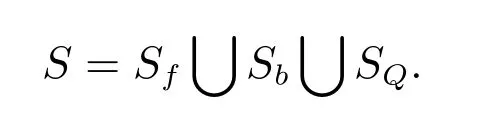
(5)式改写为
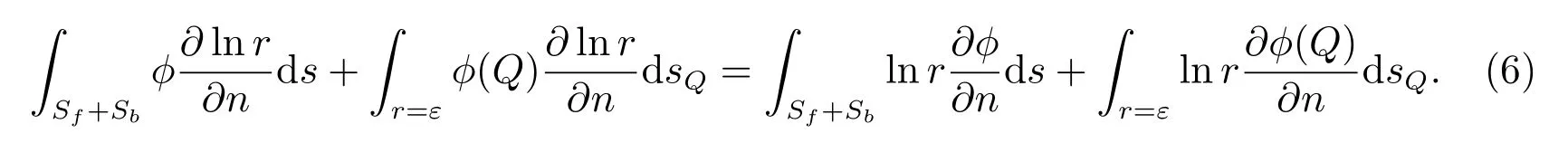
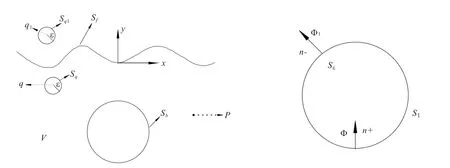
图2 源点Q 位置以及内外流场剖面
根据
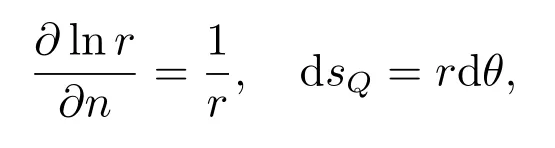
(6)式化为
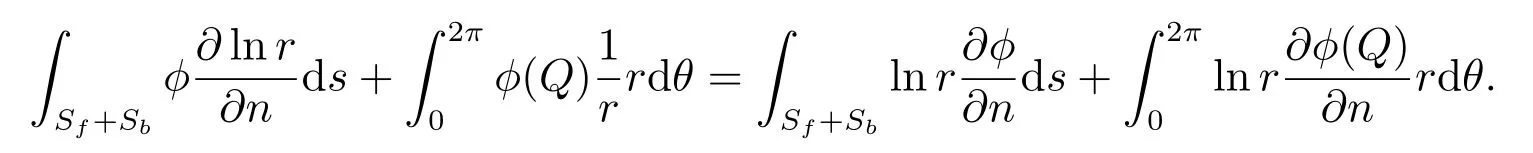
当ε →0 时
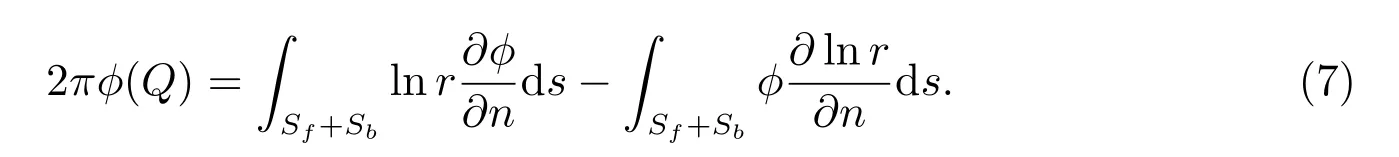
当源点Q 在流体区域的外部(图2(a)中Q1所处位置),流体区域内的点P 到源点Q 的函数ln r 取值有限.流体区域V 的边界为

(5)式改写为
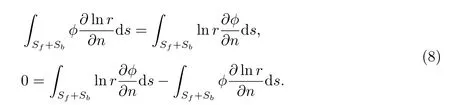
设源点Q 影响的区域为第一区域,源点Q 在第一区域的内部,φ 是第一区域速度势,φ1是流体区域V 剩余区域的速度势,如图2(b),由(7),(8)式推出对应的边界积分
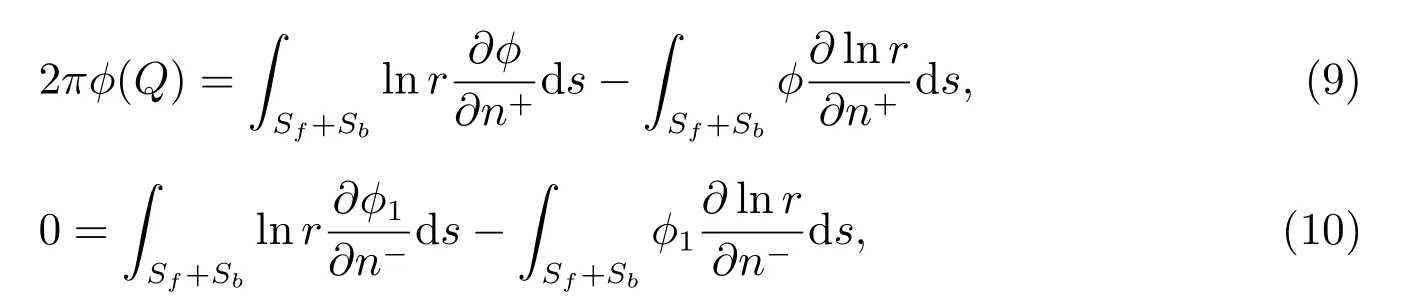
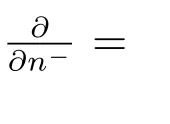
由(9)和(10)式可以推出
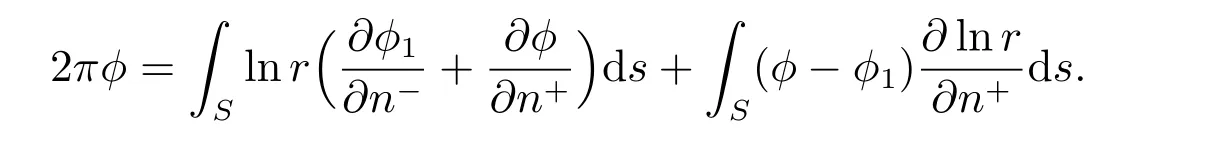
令
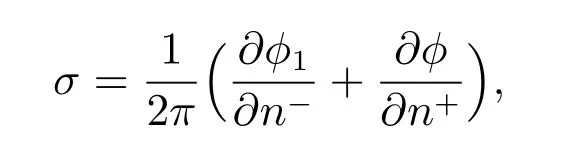
因为φ=φ1,且速度势φ, φ1关于边界S1的法向导数不连续,得到圆柱边界积分方程

3 Rankine 源分布边界积分方程离散
3.1 边界积分方程
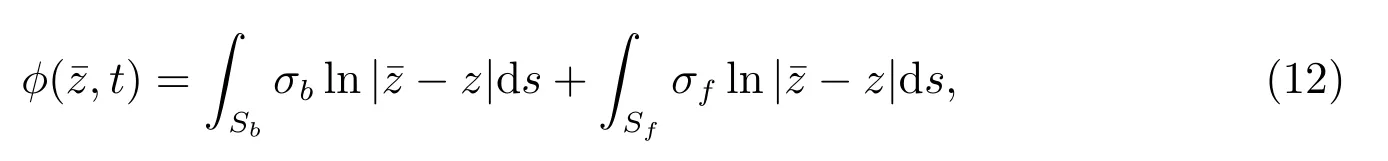
3.2 积分方程的离散化
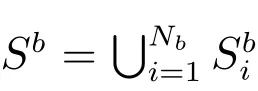
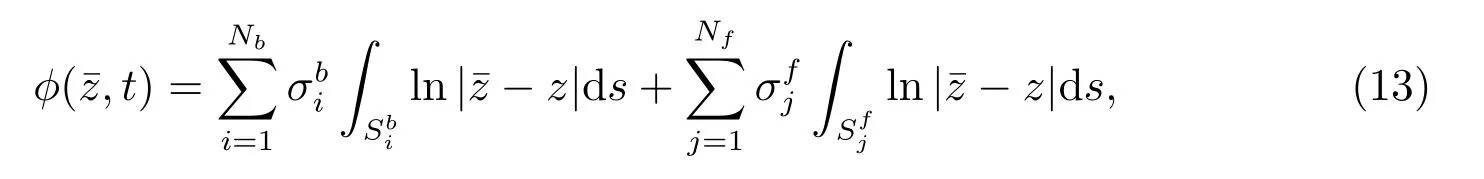
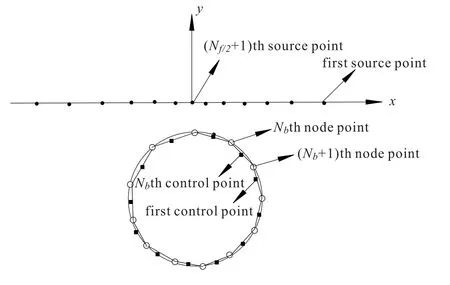
图3 t=0 时刻自由面和圆柱面面板剖分图
3.3 时间域中源点、控制点、切向量
在t = 0 自由面上放置源点时,由于流体区域是关于振动体对称的,因此,我们只讨论y 轴右边的自由面源点的放置方法.在本文中选取Nf+1=181 个源点,所以在右边自由面有Nf/2=90 个源点,70 个源点在内域,20 个源点在外域.内域源点放置方法
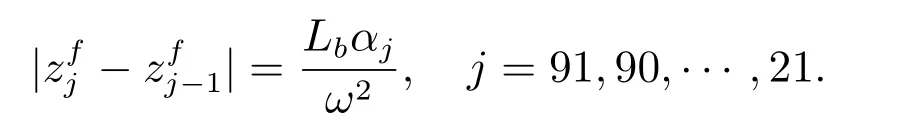
外域源点放置方法
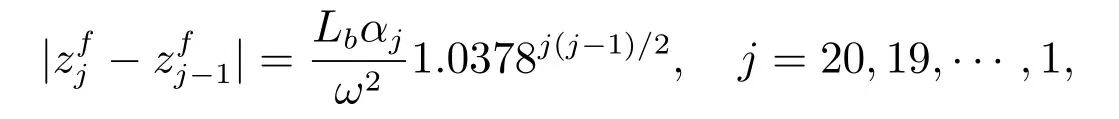
其中Lb为圆柱体面板长度,αj设置如表1.

表1 αj 的参数
由于振动体圆柱完全浸没在自由面水下,振动体面板进行均匀分割,因此振动体圆柱体的面板长度并不随时间的变化进行变化,同理物体表面单个面板的切向量亦不随时间作变化.设圆柱体表面Sb的源点,面板长度,面板切向量分别为
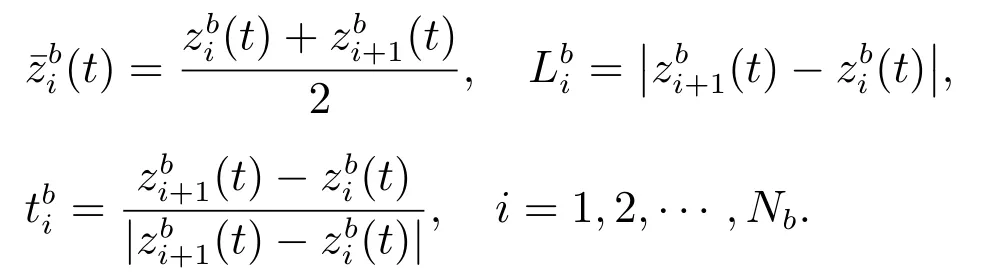
随着振动时间的变化,自由面随圆柱体振动进行变化.设自由面Sf的源点,面板长度,面板切向量分别为
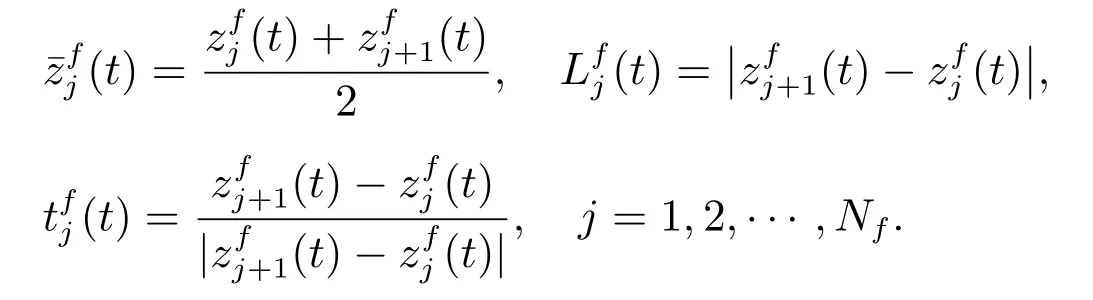
自由面边界积分方程
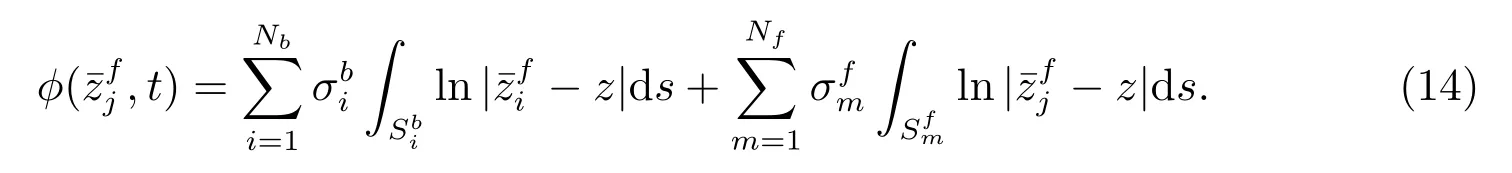
同时,圆柱体边界满足积分方程
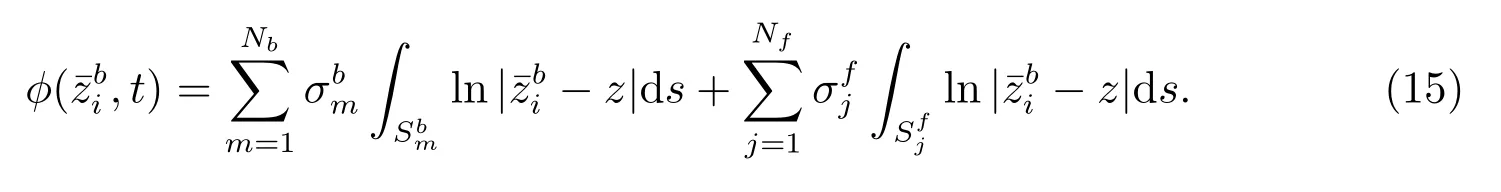
通过边界条件(1)和(15)式边界条件结合可以得到圆柱体边界积分方程
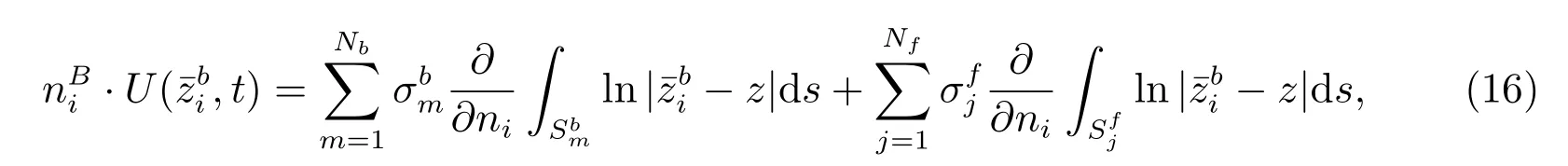
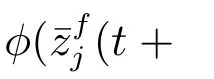
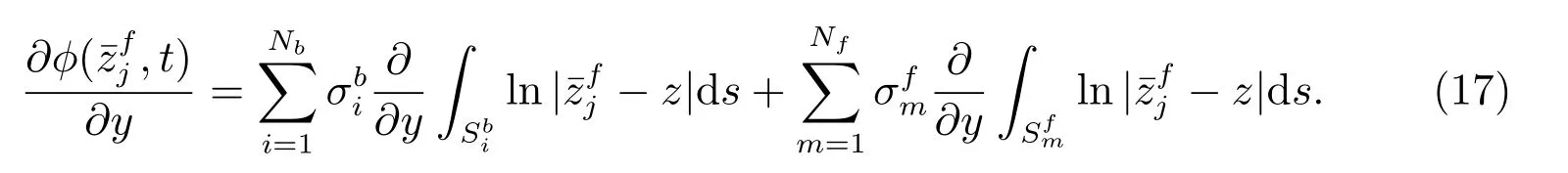
(14)式和(16)式化为下面系列代数方程
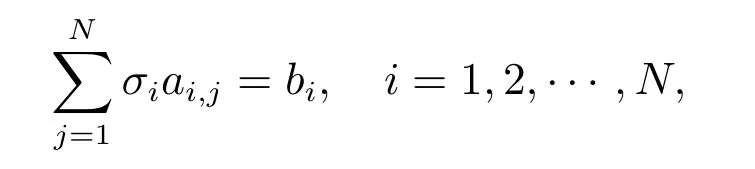
其中σi为
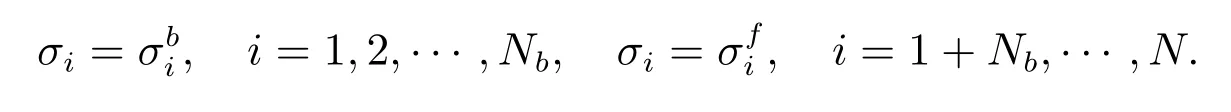
bi为
bi=Uni, i=1,2,··· ,Nb, bi=φi, i=1+Nb,··· ,N,
其中影响系数ai,j为
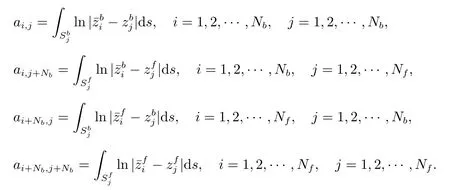
压力P 的表达式为

自由面波高η 表达式为

4 数值模拟
自由面波关于y 轴对称,下列数值模拟中,取振动圆柱体半径R = 10 m,圆柱体面板数Nb= 40,自由面面板数Nf= 180,时间步长△t = 0.001 s,浸没深度h,圆柱振动频率ω,圆柱振动振幅a,振动时间t,自由面波画图时选取原点处源点.
时域函数迭代的初始自由面边界条件
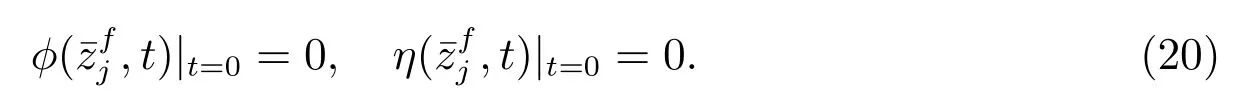
4.1 数值验证
为了验证文中采用的数值方法的准确性和有效性,本文采用自由面波高与其他文献中的数值解进行比较.
图4 采用圆柱体振动频率ω = 1.0,振幅a = 1m.图中表示自由面波的数值解与文献[16]的数值解比较图,从图中可以发现结果吻合得很好,表明本文采用的数值方法是准确有效的.

图4 自由面波高
4.2 自由面波和圆柱体压力数值模拟
首先,图5(a)研究了当浸没深度h/R = 1.5 时,不同的圆柱体振动频率下自由面波高变化规律,从图5(a)得出当振动频率增大的时候,自由面波高也相应的增大.图5(b)中取ω = 0.5,研究不同的浸没深度,得出浸没深度越大,自由面波高越小.对比图5(b)和图5(c)在不同浸没深度下的自由面波可以看到,振动频率越大,自由面波高也大,说明这种论证不仅局限于一定的浸没深度,对不同的浸没深度也有这种效果.对比图5(c)和图5(d),更加论证了上述浸没深度越小,自由面波高越大的观点.图5(f)取浸没深度h/R =1.5 一定时,数值模拟了不同振动振幅下,振动体对自由面波的影响情况,从图中可以看出,振动体振幅越大,自由面波波高越大,影响效果越明显.
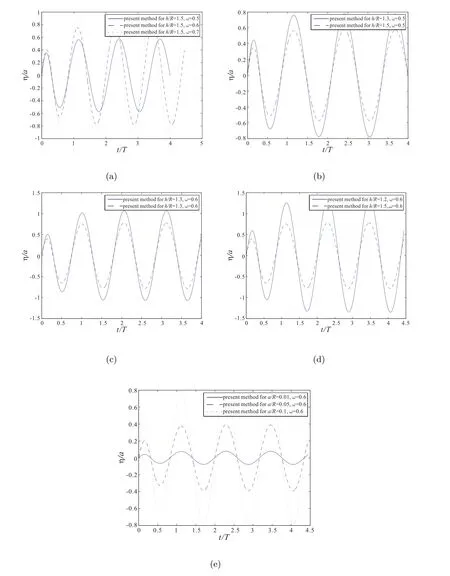
图5 不同振动参数下自由面波高变化规律
最后数值模拟了不同参数下,振动体圆柱体表面压力情况.在图6(a),取浸没深度h/R = 1.2,数值模拟了不同时刻下的圆柱体表面压力情况,可以得到不同时刻下,圆柱体的压力随圆柱体的振动在进行变化,而不是固定不变的.图6(b)中,取浸没深度h/R=1.5,对比图6(a)和图6(b)可以得到,浸没深度的越小,振动圆柱体表面压力越大.为了更形象的说明上述观点,在图6(c)中,取固定振动时刻t = 10s,在图6(c)中,可以更清晰的论证上述观点.图6(d)模拟了不同振动振幅下,圆柱体周围压力变化情况,从图6(d)中可以得出.振动振幅越大,振动圆柱体周围压力越大.
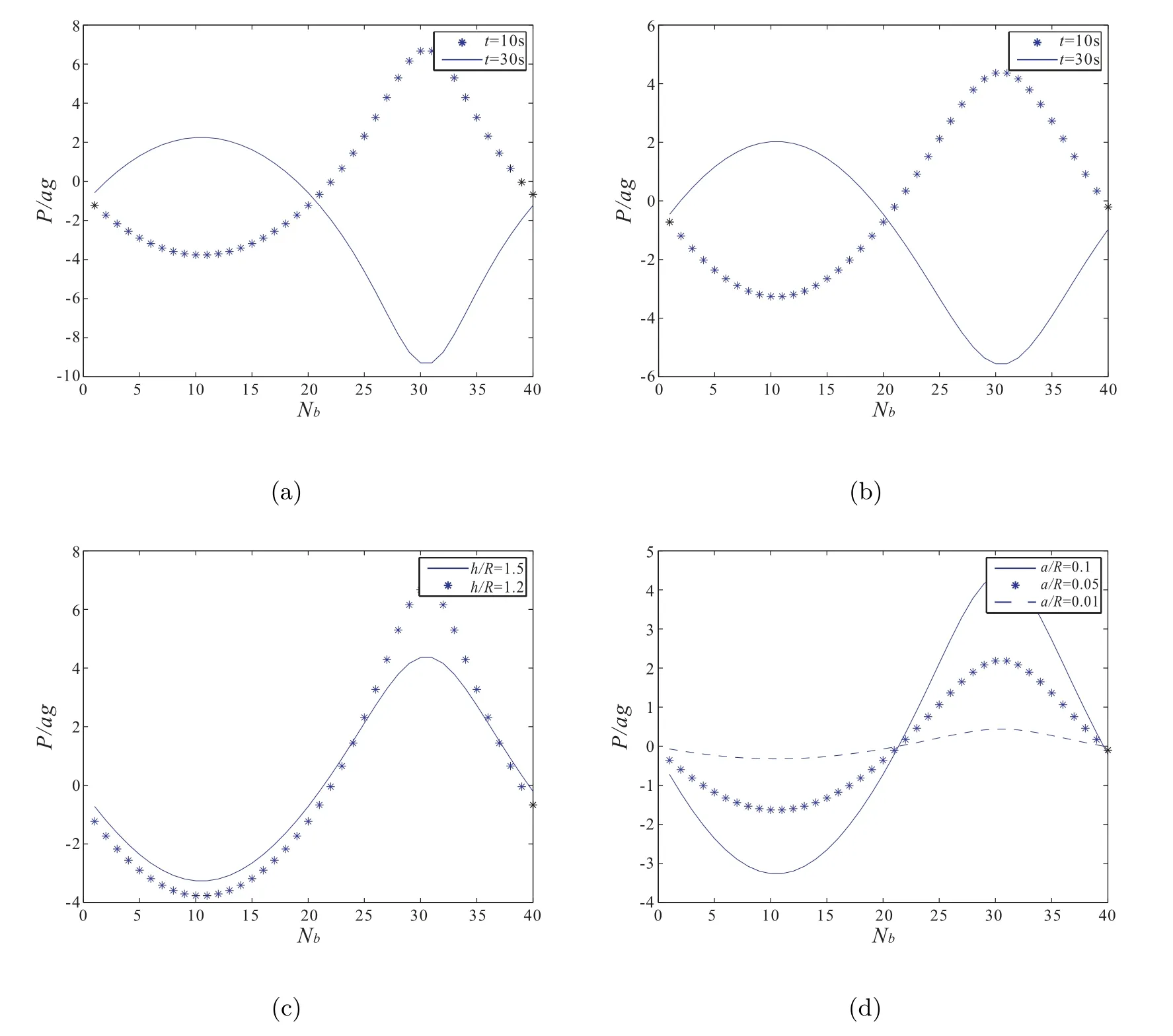
图6 不同振动参数下圆柱体表面压力变化规律
5 结论
本文基于源面板法,在二维无旋、无粘、不可压缩的流体中,数值模拟了水下振动体振动对自由面波高和圆柱体压力的影响.通过本文的数值模拟结果可知,圆柱体振动自由面波高和压力的变化与圆柱体浸没深度、圆柱体振动频率以及振动体振动振幅有关.随振动体振动频率或振动振幅的增大,自由面波高也随之增大,减小振动体浸没深度,自由面波高也逐渐增加.同时还得到,振动体振动振幅的增大也导致圆柱体表面压力的增大,随振动体浸没深度的增大,振动体周围压力反而减小.

