修正的Cahn-Hilliard 方程的大时间步长方法
胡欢欢, 李 杨, 贾宏恩
(太原理工大学数学学院,太原 030024)
1 引言
在二元合金中,为了模拟现象学中的失稳分解[1,2],Cahn 和Hilliard 于1950 年提出Cahn-Hilliard 方程.为了抑制粗化现象,Aristotelous 等人[3]提出了修正的Chan-Hilliard 方程.修正的Cahn-Hilliard 方程具有如下形式


并且Ω ∈Rd, d=2,3.u 是指混合物中两种物质之一的浓度,称为相变量.
当θ =0 时,方程(1)是经典的Cahn-Hilliard 方程[4].许多学者对经典Cahn-Hilliard方程的数值解进行了研究,例如,Zhang 和Wang[5]提出结合凸分裂方法的全离散格式,此格式满足质量守恒及原始问题的能量耗散;Guill´en-Gonz´alez 和Tierra[6]用不同方法去逼近双势阱项,并分析了关于时间分别是一阶和二阶的线性格式;Elliott 等人[7,8]利用非协调有限元Morely 元,得到了最佳L2误差估计;Liu 等人[9]用传统有限元和混合有限元两重网格方法来解Cahn-Hilliard 方程;Du 和Nicolaides[10]提出一种有限元格式来解带有Dirichlet 边界条件的Cahn-Hilliard 方程,并且证明了这种格式是稳定的.当θ = 1 时,方程(1)为特殊的修正的Cahn-Hilliard 方程[11].此时方程(1)与经典的Cahn-Hilliard 方程有很大的不同,修正的Cahn-Hilliard 方程仍用来描述相分离和粗化现象的模型[12-16].Lee 等人[17]利用隐式方法由二维截面图像重构三维实体模型;Gillette[18]应用凸分裂和谱方法对修正的Cahn-Hilliard 方程进行了研究;Choi 等人[19]利用谱方法研究了修正的Cahn-Hilliard 方程.
本文的主要工作如下:首先给出修正的Cahn-Hilliard 方程的半离散数值格式,并证明此格式的稳定性;其次,给出全离散格式及其误差估计;最后,通过数值算例来验证理论部分的正确性与有效性.
2 半离散格式及稳定性
2.1 基本理论及符号
设L2(Ω)表示平方可积函数,其内积和范数分别为

空间L∞(Ω)和Hm(Ω)的范数分别为

记

接下来定义H-1(Ω),用〈·,·〉表示H-1(Ω)和H1(Ω)上的对偶内积,记


(ζ,ξ)H-1:=(∇T(ζ),∇T(ξ))=(ζ,T(ξ))=(T(ζ),ξ),
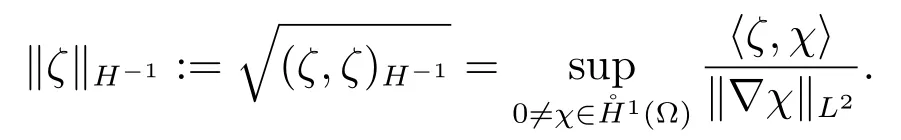
引理1(离散的Gronwall 引理)[20]设C0, Δt 是正数,并ak, bk, ck, dk是满足下面条件的非负序列
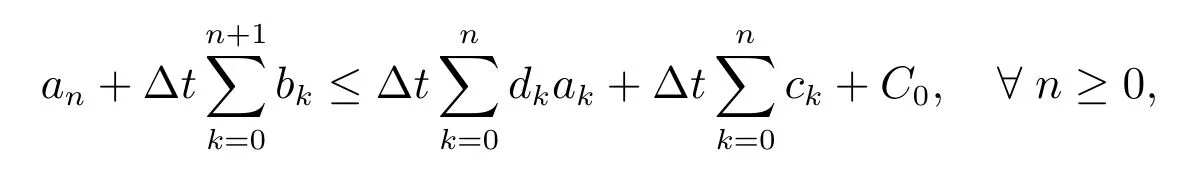
则

方程(1)保持能量耗散,若定义能量泛函

2.2 半离散格式
对于划分[0,T] : 0 = t0<t1<··· <tM= T, tn+1- tn= Δt = T/M,这里M >0 为整数,则

其中

首先考虑修正的Cahn-Hilliard 方程的一阶半隐格式

其中Δt 是时间步长,tn= nΔt,并且un是u(x,tn)的近似值.在数值模拟时,当参数ν 较小时,格式(4)无法在较大的时间步长上计算.为了解决这一问题,加O(Δtut)到格式(4)中

其中A 是正常数,格式(5)的弱形式为

2.3 稳定性分析
在证明(6)的稳定性之前,我们限制Φ′(u)满足下面的条件[21]:存在常数L 使得

定理1 若A >0,则半隐格式(6)是稳定的,即满足

证明 在方程(6)中,令v =un+1,则

使用等式2a(a-b)=a2-b2+(a-b)2,因此有
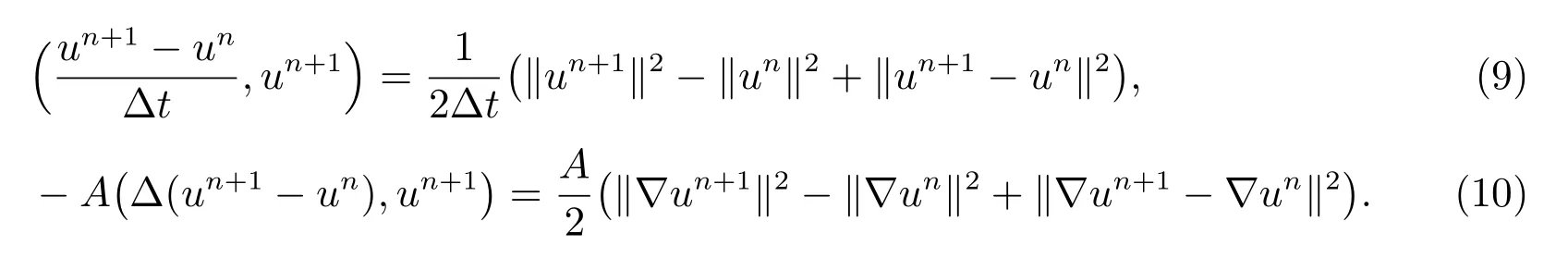

化简上述不等式并两边乘以2Δt,对n 从0 到k(0 ≤k ≤M -1)进行求和,得到

利用引理1,有
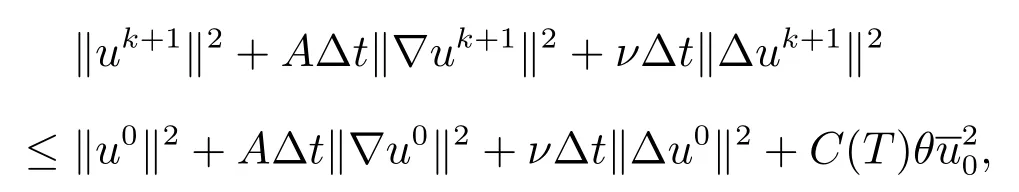
定理证明完成.
3 全离散格式及误差估计
3.1 全离散格式
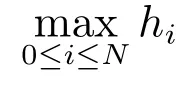
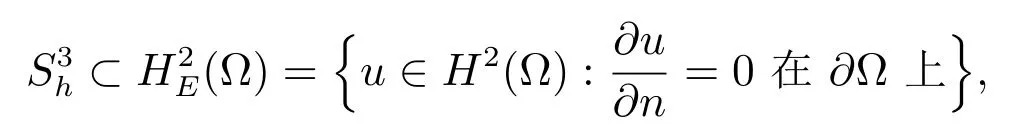
且存在不依赖h 的常数c >0,满足逆不等式
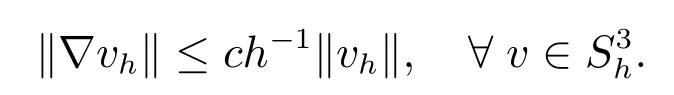
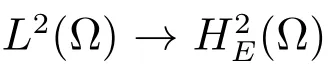

类似地,定义方程(1)的半离散格式:求uh(t):(0,T]→S3h,使得
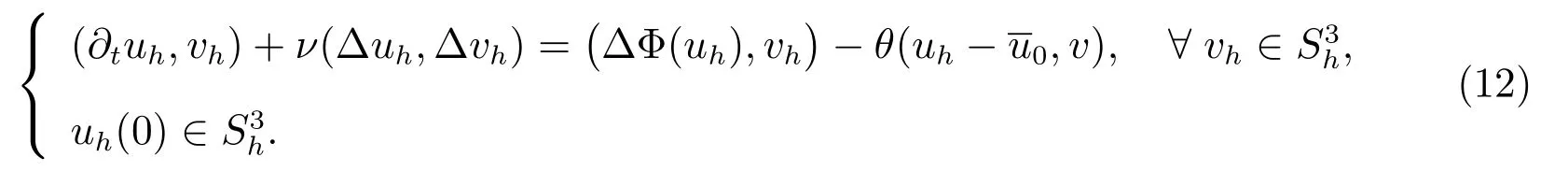

3.2 误差分析

从不等式
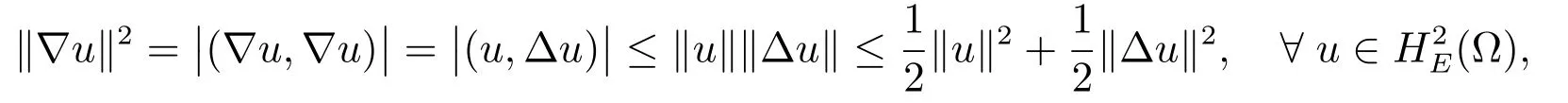
可以得到
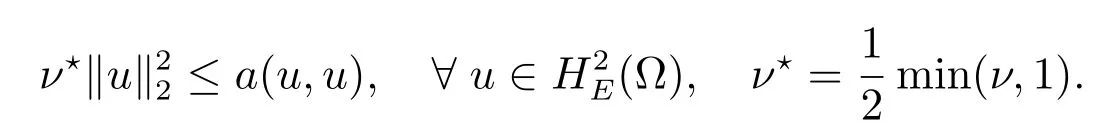
根据双调和方程的有限元分析[22],得到
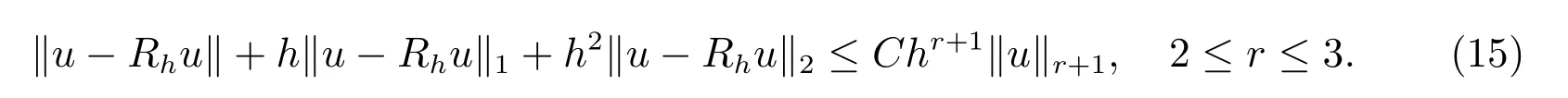


在方程(16)中,令t=tn+1并减去方程(13),则有
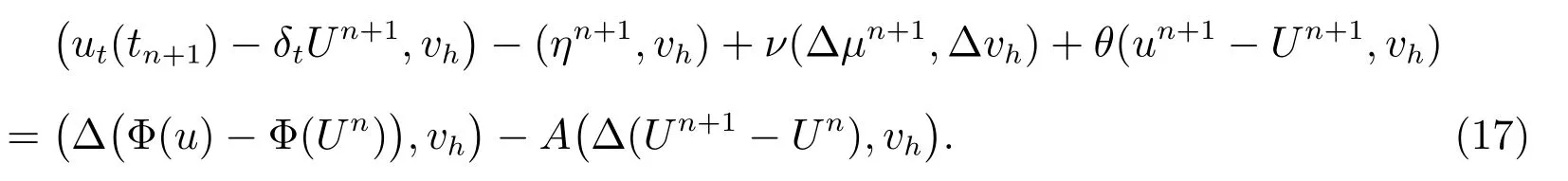
在方程(17)中

故有

定理2 记u(t)和Un+1分别是方程(11)和(13)的解,如果u(0)∈H4(Ω),满足‖u(0)-U0‖≤Ch4‖u(0)‖4,网格比Δt/h2≤c,当h 足够小时,则存在不依赖h, Δt, n 的C =C(u)满足

证明 在证明之前,先给出一个先验假设[23]:若0 <h <h0,则存在h0满足

在方程(18)中令vh=μn+1,则有

使用Cauchy 不等式和Young 不等式,所以


利用δtμn+1的定义和Cauchy 不等式,可以得到
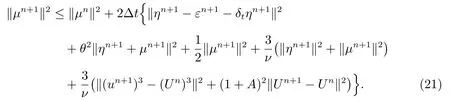
结合方程(3),(16)和(20),有下面的估计
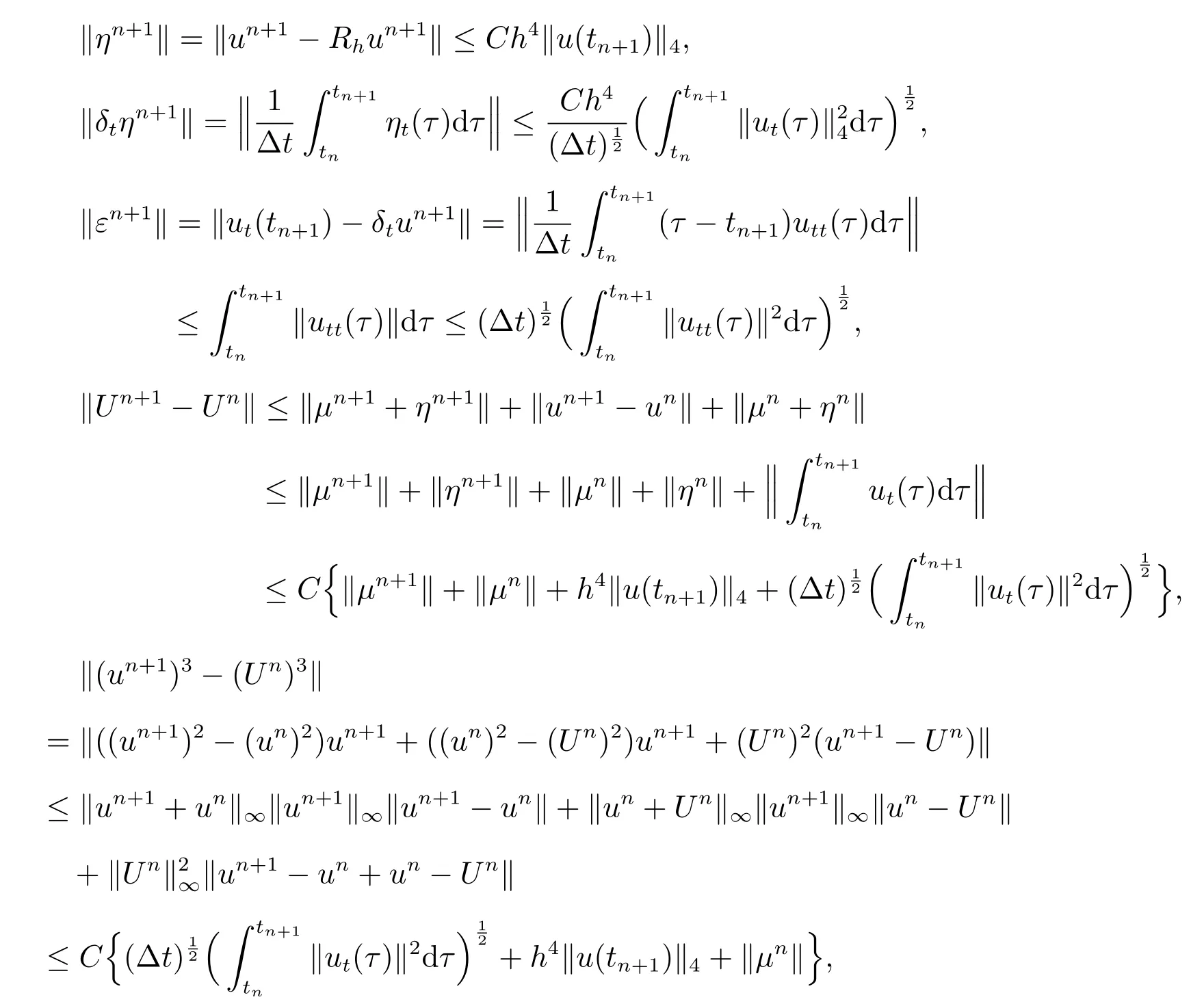
其中用到下面的不等式

把上述不等式带入方程(21),得到

上式从n=1 加到M,注意到
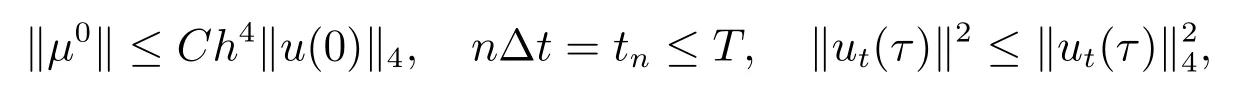
则有


根据离散的Gronwall 引理,则有‖μn+1‖ ≤C(h4+Δt),因此,结合(15)和三角不等式,所以有
‖un+1-Un+1‖≤‖μn+1‖+‖ηn+1‖≤C(h4+Δt).
4 数值实验
本小节,利用数值算例来验证理论分析的准确性和有效性.
4.1 误差和收敛性
考虑二维修正的Cahn-Hilliard 方程,计算区域为Ω=[0,2π]2,初值为u0=0.2 sin(x)sin(y).由于方程(1)的精确解未知,我们选取Δt = 0.0001 和N = 128 时,所计算的数值解作为精确解.
表1 给出了当ν = 0.03 时,A, θ, Δt 取不同值时的L2误差.通过观察表1 的数据,可以看出当A 取固定值时,全离散格式是稳定的,并且关于时间是一阶收敛,和理论分析一致.
表1 L2 误差:ν =0.03, T =1, h=

表1 L2 误差:ν =0.03, T =1, h=
A Δt θ =0 θ =2 θ =5 0 0.01 0.00382036 0.0152565 0.167332 0.005 0.00212644 0.00702886 0.0877675 0.0025 0.00108075 0.00339221 0.0441148 0.00125 0.00052603 0.00168505 0.0213931 1 0.01 0.0107831 0.0530077 0.311978 0.005 0.00623478 0.0219408 0.178414 0.0025 0.00340485 0.00992049 0.0943016 0.00125 0.00173112 0.00473141 0.047645
续表1 L2 误差:ν =0.03, T =1, h=
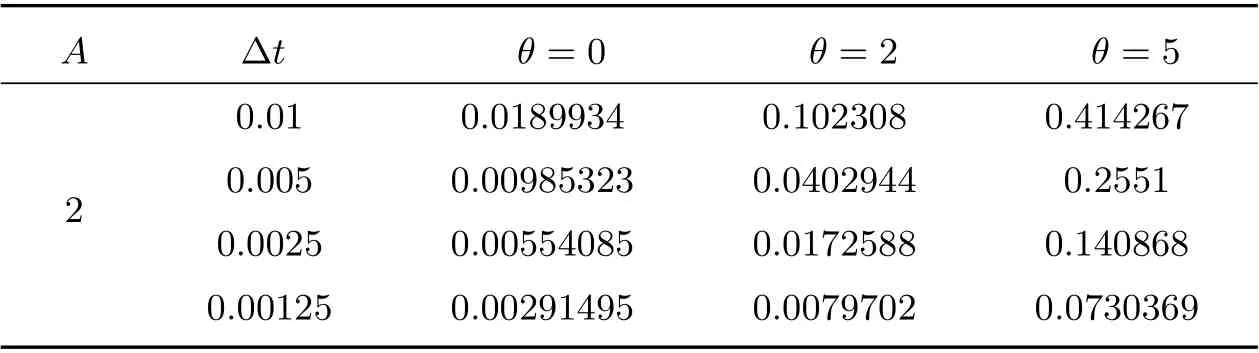
续表1 L2 误差:ν =0.03, T =1, h=
A Δt θ =0 θ =2 θ =5 2 0.01 0.0189934 0.102308 0.414267 0.005 0.00985323 0.0402944 0.2551 0.0025 0.00554085 0.0172588 0.140868 0.00125 0.00291495 0.0079702 0.0730369
当ν = 0.03 时,表2、表3、表4 分别呈现了A 取0,1,2 时,θ 分别取0,2,5 的空间收敛阶.通过观察表2、表3、表4,可以发现空间收敛阶和理论分析相符.

表2 收敛阶:ν =0.03, θ =0

表3 收敛阶:ν =0.03, θ =2

表4 收敛阶:ν =0.03, θ =5
4.2 能量稳定

图1 能量曲线
4.3 等值线


图2 等值线:ν =0.03, θ =2,左:A=0, Δt=0.001,中:A=1, Δt=0.005,右:A=2, Δt=0.01

图3 等值线:ν =0.03, A=1,左:θ =0, Δt=0.001,中:θ =2, Δt=0.005,右L:θ =5, Δt=0.01
在图2 中,第1 列,θ = 2, A = 0, Δt = 0.001;第2 列,θ = 2, A = 1, Δt =0.005;第3 列,θ = 2, A = 2, Δt = 0.01.同样地,在图3 中,第1 列,θ = 0, A =1, Δt = 0.001;第2 列,θ = 2, A = 1, Δt = 0.005;第3 列,θ = 5, A = 1, Δt =0.01.观察图3,不难发现,θ >0 会抑制相分离.通过观察图2 和图3,可知:“A-项”确实起到了增加时间步长的作用,但不恰当的A 值会导致数值解的发散,即当计算时间步长比较大时,大时间步长方法得到的解可能不是真实解.
5 结论
本文中,我们对于修正的Cahn-Hilliard 方程的大时间步长方法进行了研究.为解决由于非线性和小参数带来的影响,提出了稳定的离散格式,从理论上证明了方法的稳定性,并给出了误差估计.最后,通过数值实验证明了方法的有效性.

