不同损失下随机截尾BurrXII分布的Bayes统计分析

季海波

(宿迁学院 文理学院， 江苏 宿迁 223800)

0 引言

1942年，Burr在研究关于分布函数的微分方程,时引入了Burr分布. BurrXII分布在保险精算学、环境环境科学、社会经济学等领域都有比较广泛的应用,还被列为精算师常用的八大分布之一，这也充分说明了该分布的重要性。通过截尾的方式来降低可靠性寿命试验的成本和减少试验的周期，其中比较常用的截尾方式有定数截尾和定时截尾，这两种截尾下的相关分布参数的Bayes估计的结果已经比较完整了[1-3]. 例如，随机截尾情形下Rayleigh分布和Pareto分布参数的Bayes估计[4-5].但目前研究MLINEX和复合MLINEX损失下随机截尾BurrXII分布参数的Bayes估计的学者却不多，故本文将研究该分布参数的估计问题.

假设X1,X2,X3,…,Xn,表示随机截尾试验中受试产品的寿命，是一列相互独立且都服从BurrXII分布的随机变量，其密度函数和分布函数分别为

f(x;θ)=θγxγ-1(1+xγ)-(1+θ)

(1)

(2)

为了估计方便，假设式(1)、式(2)中的参数γ已知，θ未知.

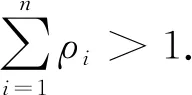
(3)

1 参数θ的Bayes估计

接下来，主要研究BurrXII分布在已知γ的情形下，未知参数θ在MLINEX及复合MLINEX损失下，利用随机截尾试验找出该参数的Bayes估计.

本文取参数θ的广义先验分布，其先验密度函数为

π(θ)=1,θ>0

(4)

由式(3)、式(4)可得参数θ的后验条件密度函数为

(5)

其中

由式(5),有

(6)

文[6]中给出了MLINEX损失函数为:

(7)

本文仅考虑c>0的情形，在此损失函数下有如下定理：

定理1 在损失函数(7)下，若参数θ取广义先验分布时，则分布(1)中参数θ的Bayes估计为:

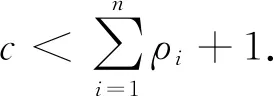
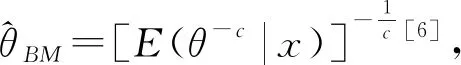
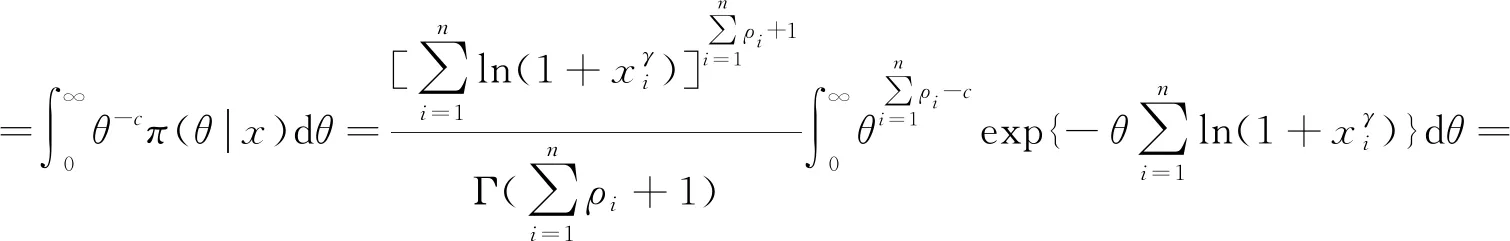
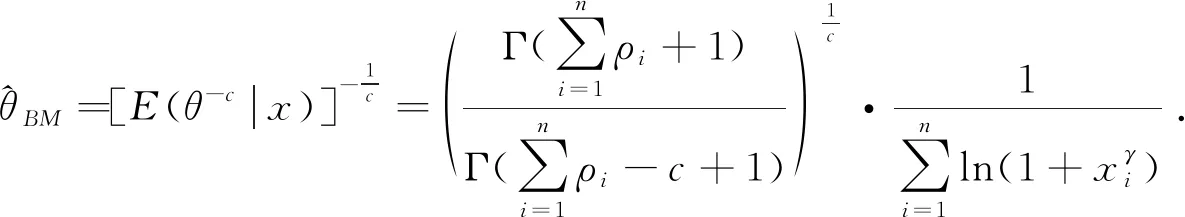
文[7]给出了复合MLINEX对称损失函数如下，

(8)

则在该损失函数下有如下结论.

定理2 在损失函数(8)下，若参数θ广义先验分布时，则分布(1)中参数θ的Bayes估计为:

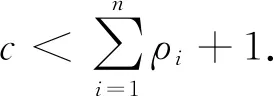
从而有

2 参数θ的区间估计

由Bayes置信区间的定义即可得到随机截尾下的置信度为1-α的置信区间，

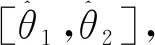
3 Monte-Carlo随机模拟

下面先取γ=1.5，然后通过Monte-Carlo方法进行模拟.利用算法[8]来产生随机截尾的样本. 首先需要给定每一个受试产品的截尾时间y1,y2,…,yn,再利用这些样本数据及两个定理的精确表达式给出两个不同损失下的BurrXII分布参数θ的Bayes估计，利用Matlab将算法随机模拟1 000次，模拟结果见表1.

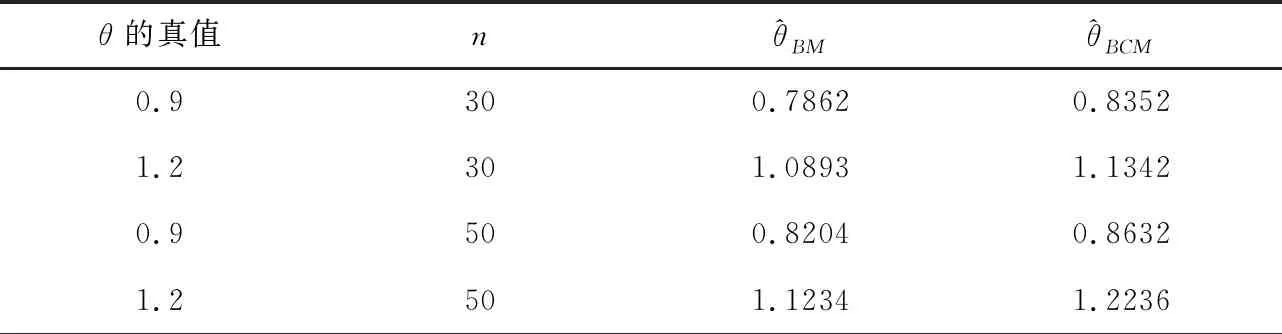
表1 两个损失下各项指标的Bayes估计模拟值(c=2)

上述模拟结果表明: 随着样本量的增大，两个Bayes估计都是越来越接近θ的真值；横向比较来看，在相同的真值和样本量下，都是复合MLINEX对称损失函数下的Bayes估计较为优良.故在求随机截尾情形下BurrXII分布参数θ的Bayes估计时，相比较这两个损失函数，优先推荐利用复合MLINEX对称损失函数.