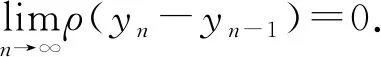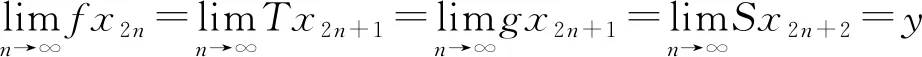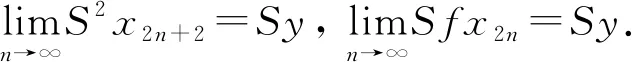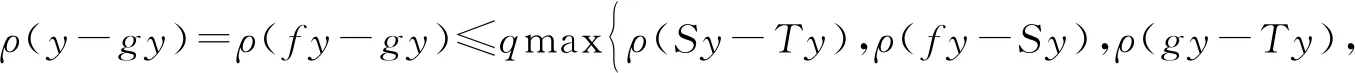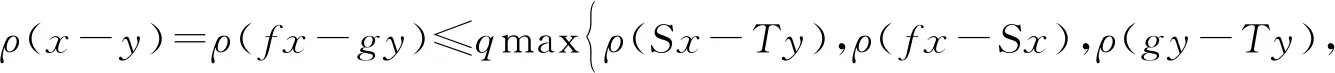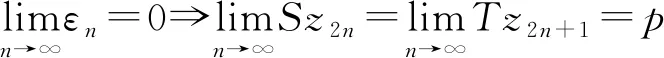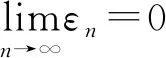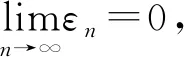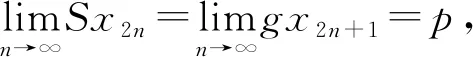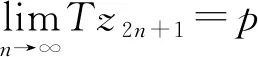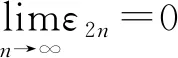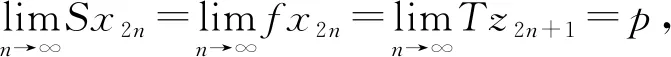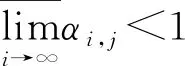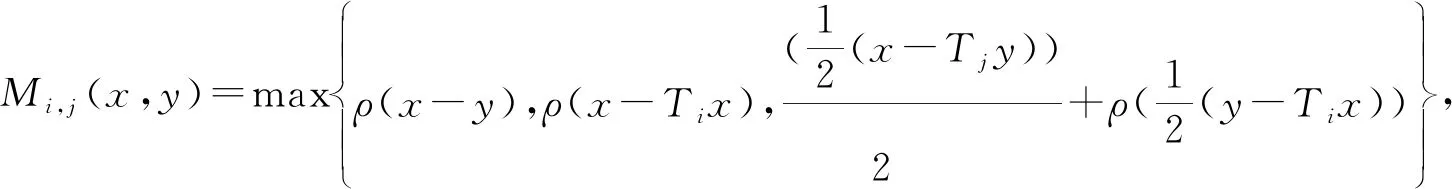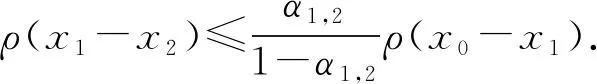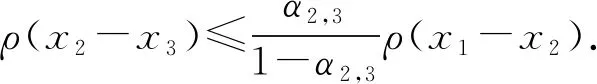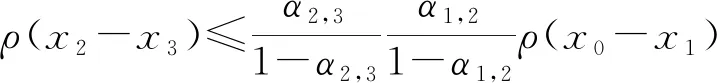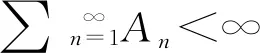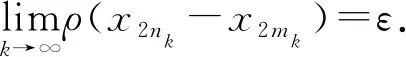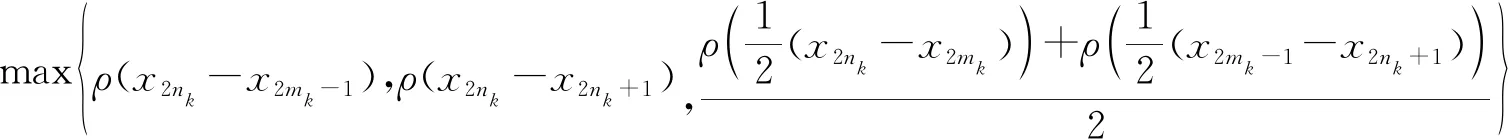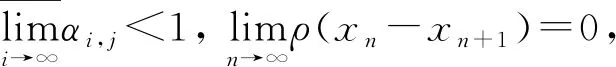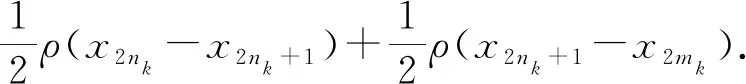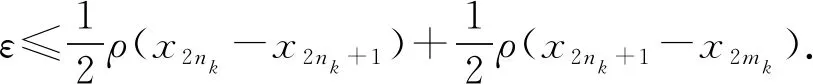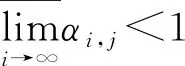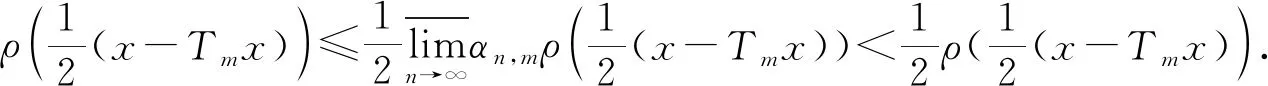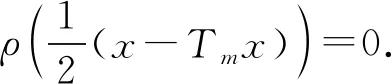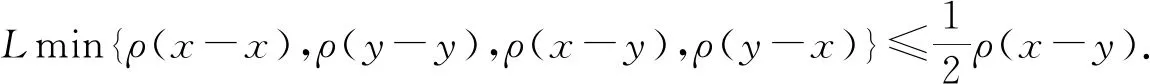模空间中若干公共不动点问题的研究

李 泽, 魏 超

(南京财经大学 应用数学学院， 江苏 南京 210023)

0 引言及预备知识

模空间作为一类较为抽象的空间, 扩展了包括Lp空间、Orlicz空间在内的许多空间框架, 引起了众多学者的关注[1-3].近年来, 模空间中的公共不动点问题得到国内外学者广泛深入的研究. 2007年, Nabizadeh E利用Δ2条件, 在模空间中给出了一类非线性收缩映射及渐近收缩映射的不动点定理[4]; 2008年, Khamsi M A给出了模空间中没有Δ2条件的拟压缩映射的不动点定理[5]; 2012年, Wang X等人将Banach空间中的渐近逐点非扩张映射的概念引入到模空间中, 并在模空间中证明了该映射具有不动点[6]; 2016年, Özturk M等人给出了模空间中ψ-φ广义压缩映射的概念, 并且证明了一类公共不动点定理[7].

本文拟在模空间中探讨公共不动点问题, 将度量空间中的多个映射及一类无限族自映射的公共不动点定理推广至模空间, 进一步丰富模空间的相关理论.

定义1 设X为数域K=R或K=C上的任一向量空间. 对于X中的∀x,y, 泛函ρ:X→[0,+∞)被称为X上的模, 如果:

(a)ρ(x)=0当且仅当x=0;

(b)ρ(αx)=ρ(x)当α为标量时且|α|=1;

(c)ρ(αx+βy)≤ρ(x)+ρ(y), 如果α,β≥0且α+β=1.

若条件(c)被ρ(αx+βy)≤αsρ(x)+βsρ(y), 其中αs+βs=1,α,β≥0且s∈(0,1]替代, 则称模ρ为s-凸模. 如果s=1, 则称模ρ为凸模. 若向量空间Xρ={x∈X|ρ(λx)→0,当λ→0}, 则称向量空间Xρ为模空间.

定义2 设ρ为定义在X上的模,Xρ为模空间.

(a) 对于序列{xn}⊂Xρ, 点x∈Xρ, 若n→∞时, 有ρ(xn-x)→0, 则称序列{xn}ρ-收敛于点x. 记为xn→x；

(c) 若Xρ中的每个柯西列都ρ-收敛, 则称Xρ为完备的模空间；

(d) 当模ρ满足Δ2条件时： 若n→∞时,ρ(xn)→0可推出ρ(2xn)→0；

(e) 设映射S为Xρ上的自映射, 若xn→x时, 有Sxn→Sx, 则称映射S为Xρ上的连续映射；

(f) 若xn→x时, 有ρ(xn)→ρ(x), 则称模ρ为连续的.

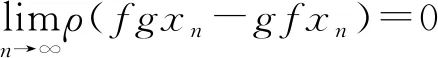
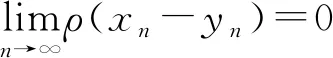
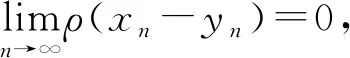
1 主要结果

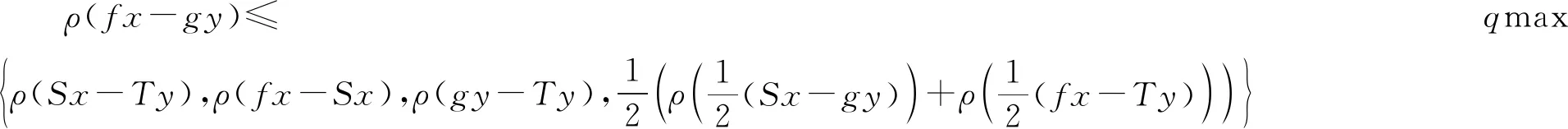
证明任取x0∈Xρ, 由于f(Xρ)⊂T(Xρ), 故存在x1∈Xρ使得fx0=Tx1. 又因为gx1∈S(X), 则存在x2∈X使得gx1=Sx2. 故一般地, 有fx2n=Tx2n+1和gx2n+1=Sx2n+2. 进一步地设y2n=fx2n=Tx2n+1,y2n+1=gx2n+1=Sx2n+2,

第1步: 证明序列{yn}为柯西列. 考虑到

ρ(y2n-y2n+1)=ρ(fx2n-gx2n+1)≤

若

ρ(y2n-y2n+1)>ρ(y2n-1-y2n),

由上式得ρ(y2n-y2n+1)

由于q<1, 故ρ(y2n-y2n+1)

因此

ρ(y2n-y2n+1)<ρ(y2n-1-y2n),

从而ρ(y2n-y2n+1)

类似可得

ρ(y2n-1-y2n)

依此类推,可得

ρ(yn-yn-1)<…

对于任意的n>m,n,m∈N, 由于ρ(2x)=2ρ(x), 故有

ρ(yn-yn-1)+…+ρ(ym+2-ym+1)+ρ(ym+1-ym)≤

qn-1ρ(y1-y0)+…+qm+1ρ(y1-y0)+qmρ(y1-y0)≤

第2步: 证明点y为映射f,g,S,T的公共不动点.

ρ(fx-gy)≤

其中，取x=Sx2n,y=x2n+1时, 有

由ρ连续, 对上式两边取极限, 有ρ(Sy-y)≤qρ(Sy-y).

由于q<1, 故ρ(Sy-y)=0, 从而有Sy=y成立. 同理可得Ty=y成立. 在

上式中，取x=y,y=x2n+1, 由Sy=Ty=y，可得fy=y成立.

最后由

可得gy=y成立.

因此，有Sy=Ty=fy=gy=y.

第3步: 证明点y为唯一的公共不动点.若还存在一点x为映射f,g,S,T的公共不动点, 则有

成立. 由于q<1, 故ρ(x-y)=0, 从而有x=y.

故映射f,g,S,T有唯一的公共不动点.

注1 定理1将文[8]中的相关结果从b-度量空间推广到模空间. 由于模空间不满足次可加性, 因此本定理的证明方法也不同于文[8].

考虑到f,g,S,T分别为完备的模空间Xρ上的自映射, 且有f(Xρ)⊂T(Xρ),g(Xρ)⊂S(Xρ); 任取x0∈Xρ, 存在x1∈Xρ使得fx0=Tx1. 又因为gx1∈S(X), 则存在x2∈X使得gx1=Sx2. 故一般地, 则有fx2n=Tx2n+1和gx2n+1=Sx2n+2. 进一步地设

y2n=fx2n=Tx2n+1，y2n+1=gx2n+1=Sx2n+2

(*)

至此,可以得到模空间中一序列{yn}. 定理2指出迭代序列是收敛的,并且迭代程序是稳定的.

定理2设f,g,S,T分别为完备的模空间Xρ上的自映射, 且有f(Xρ)⊂T(Xρ),g(Xρ)⊂S(Xρ); 映射S,T是连续的且映射对{f,S},{g,T}相容. 若f,g,S,T满足:ρ(4(fx-gy))≤qρ(Sx-Ty),q∈[0,1). 凸模ρ连续, 满足Δ2条件及ρ(2x)=2ρ(x), 则，

(a) 映射f,g,S,T有公共不动点p, 且由(*)式迭代产生的序列{yn}收敛到点p；

ρ(p-Tz2n+1)≤ρ(2(Tz2n+1-fz2n))+ρ(4(fz2n-gx2n+1))+ρ(4(gx2n+1-p))≤

ρ(2(Tz2n+1-fz2n))+qρ(Sz2n-Tx2n+1))+ρ(4(gx2n+1-p))≤

ρ(2(Tz2n+1-fz2n))+qρ(2(Sz2n-gz2n+1))+qρ(2(gz2n+1-Tx2n+1))+ρ(4(gx2n+1-p))≤

ρ(2(Tz2n+1-fz2n))+qρ(2(Sz2n-gz2n+1))+qρ(2(gz2n+1-fx2n))+ρ(4(gx2n+1-p))≤

ρ(2(Tz2n+1-fz2n))+qρ(2(Sz2n-gz2n+1))+qρ(4(gz2n+1-fx2n))+ρ(4(gx2n+1-p))≤

ρ(2(Tz2n+1-fz2n))+qρ(2(Sz2n-gz2n+1))+q2ρ(Tz2n+1-Sx2n))+ρ(4(gx2n+1-p)).

ρ(p-Tz2n+1)≤q2ρ(p-Tz2n+1),q<1.

ρ(p-Sz2n)≤ρ(2(gz2n+1-Sz2n))+ρ(4(gz2n+1-fx2n))+ρ(4(fx2n-p))≤

ρ(2(gz2n+1-Sz2n))+qρ(Tz2n+1-Sx2n)+ρ(4(fx2n-p))≤

ρ(2(gz2n+1-Sz2n))+qρ(2(Tz2n+1-p))+qρ(2(Sx2n-p))+ρ(4(fx2n-p)).

对上式两边取n→∞, 由

定理3 设Xρ为完备的模空间, 凸模ρ连续, 满足Δ2条件.αi,j≥0(i,j∈N+)且满足:

设{Tn}为Xρ上的自映射序列且满足:

ρ(Tix-Tjy)≤αi,jMi,j(x,y)+LNi,j(x,y), ∀x,y∈Xρ,i≠j,L≥0,

其中

Ni,j(x,y)=min{ρ(x-Tix),ρ(y-Tjy),ρ(x-Tjy),ρ(y-Tix)}.

则所有的映射序列{Tn}在模空间Xρ上有唯一公共不动点.

证明取x0∈Xρ, 由xn=Tn(xn-1)构造序列{xn}. 接下来，分以下4步证明.

第1步: 证明当n→∞时, 有ρ(xn-xn+1)→0. 由ρ(Tix-Tjy)≤αi,jMi,j(x,y)+LNi,j(x,y)式, 有

ρ(x1-x2)=ρ(T1x0-T2x1)≤α1,2M1,2(x0,x1)+LN1,2(x0,x1)=

α1,2max{ρ(x0-x1),ρ(x1-x2)}≤α1,2(ρ(x0-x1)+ρ(x1-x2)).

从而有

同理有

依此类推, 得到

第2步: 证明序列{xn}为ρ-柯西列.

从而由此不等式可得

ε≤ρ(x2nk-x2mk)=ρ(x2nk-x2nk-1+x2nk-1-x2mk)≤

ρ(2(x2nk-x2nk-1)+ρ(2(x2nk-1-x2mk))<ε+ρ(2(x2nk-x2nk-1).

在ρ(Tix-Tjy)≤αi,jMi,j(x,y)+LNi,j(x,y)中，取x=x2nk,y=x2mk-1, 则有

ρ(x2nk+1-x2mk)=ρ(T2nk+1x2nk-T2mkx2mk-1)≤

α2nk+1,2mkM2nk+1,2mk(x2nk,x2mk-1)+LN2nk+1,2mk(x2nk,x2mk-1).

其中

M2nk+1,2mk(x2nk,x2mk-1)=

N2nk+1,2mk(x2nk,x2mk-1)=min{ρ(x2nk-x2nk+1),ρ(x2mk-1-x2mk),ρ(x2nk-x2mk),ρ(x2mk-1-x2nk+1)}.

由ρ(2(x2nk-1-x2mk))<ε可得

ρ(x2nk+1-x2mk)=ρ(x2nk+1-x2nk+x2nk-x2nk-1+x2nk-1-x2mk)≤

ρ(2(x2nk+1-x2nk+x2nk-x2nk-1))+ρ(2(x2nk-1-x2mk))≤

ρ(4(x2nk+1-x2nk))+ρ(4(x2nk-x2nk-1))+ρ(2(x2nk-1-x2mk))≤

ρ(4(x2nk+1-x2nk))+ρ(4(x2nk-x2nk-1))+ε.

ρ(x2nk-x2mk-1)=ρ(x2nk-x2nk-1+x2nk-1-x2mk+x2mk-x2mk-1)≤

ρ(2(x2nk-x2nk-1+x2mk-x2mk-1))+ρ(2(x2nk-1-x2mk))≤

ρ(4(x2nk-x2nk-1))+ρ(4(x2mk-x2mk-1))+ρ(2(x2nk-1-x2mk))≤

ρ(4(x2nk-x2nk-1))+ρ(4(x2mk-x2mk-1))+ε.

注意到

ρ(x2mk-1-x2mk)+ρ(x2mk-x2nk+1))<

ε+ρ(x2mk-1-x2mk)+ρ(4(x2nk-1-x2nk))+ρ(4(x2nk-x2nk+1)).

ρ(x2nk-x2nk-1)+ρ(x2nk-1-x2mk)≤ρ(x2nk-x2nk-1)+ρ(2(x2nk-1-x2mk))<

ρ(x2nk-x2nk-1)+ε.

结合M2nk+1,2mk(x2nk,x2mk-1)可得

M2nk+1,2mk(x2nk,x2mk-1)=

由ρ是凸模,ρ(x2nk-x2mk)≥ε可得

第3步: 证明映射序列{Tn}在模空间Xρ上有公共不动点.

因为{xn}为ρ-柯西列且模空间Xρ为完备的, 所以存在一点x∈Xρ使得xn→x. 从而对于任意正整数m, 有

ρ(x-xn)+ρ(xn-Tmx)=ρ(x-xn)+ρ(Tnxn-1-Tmx)≤

Lmin{ρ(xn-1-xn),ρ(x-xn),ρ(x-Tmx),ρ(xn-1-Tmx)}.

因此,有

从而有ρ(x-y)=0, 即x=y. 故映射序列{Tn}在模空间Xρ上公共不动点是唯一的. 至此定理得证.

本定理将文[9]中的相关结果从度量空间推广到模空间. 文在模空间中考虑公共不动点问题, 引入相容映射和一类无限族自映射的概念, 将度量空间中的相关公共不动点定理进行推广, 所做的工作将丰富模空间的相关理论.