大跨屋盖风载特性风洞试验研究

李驰宇，戴益民，刘泰廷，谷庆航

（1.结构抗风与振动控制湖南省重点实验室，湘潭411201；2.湖南科技大学 土木工程学院，湘潭411201）

0 引言

大跨度结构具有质量轻、柔性大、阻尼小、结构自振周期与风速的卓越周期相近等特点，因此对风荷载十分敏感，风荷载也成为此类建筑设计时的主要控制荷载.当风作用于大跨度结构建筑上时，受几何构造、周边布局和地貌影响时会使气流分离、漩涡脱落以及再附的影响使得其风荷载特性分析变得极为复杂，当气流的波动强度较大时，结构会产生风致振动，对结构安全造成影响.李宇等［1］采用刚性模型测压试验与CFD数值模拟的方式研究了两种曲面组合形式不同的屋盖风压;张雪等［2］通过多次独立重复采样风洞试验，获得了大量的试验数据，拟合结果表明极小值更符合广义极值分布；吴立等［3］通过数值模拟研究了干扰体对建筑的风致干扰机理，结果表明干扰体的位置与形状很大程度上影响了大跨结构建筑屋盖的实际平均风压；郎亚超［4］基于FLUENT软件，对某会议中心大跨屋盖表面风荷载特性进行了研究，结果表明当建筑物平面尺寸一定时，随着高宽比的增大，屋盖表面负压随之增大；聂燕松［5］在K-means聚类分析方法基础上建立了平均风荷载分区法，通过编制的MATLAB程序对风洞数据进行了分析，给出了不同几何形式的屋面在来流下的体形系数、脉动体型系数分区建议；梁晓娟［6］研究了屋盖表面极值风压随模型几何参数的变化规律.结果表明，随屋盖矢跨比增大，悬挑屋檐短边方向极值风压增大，长边方向极值风压减小；当屋盖矢跨比不变，幕墙单面开洞时，极值风压增大，对屋盖最不利；幕墙双面对称开孔时，极小风压值减小，对屋盖有利；戴益民［7-8］、秦乐等［9］对平屋盖表面风荷载特性进行了研究，给出了风向角、风速、场地条件等对风荷载的影响；另外，刘娟［10］、齐鹏［11］、李秋胜［12］、孙瑛［13］、沈国辉［14］等人都对不同几何形式的大跨屋盖结构风荷载特性进行了不同角度的探究，其中一些结论可以相互印证，总结研究结果可以得出处于强风作用下的大跨度屋盖主要破坏形式一般分为整体倒塌、屋盖角部破坏、屋盖整体破坏、围护结构破坏等四种，其中建筑物的跨度越大，所造成的影响就越大.我国现行《建筑结构荷载规范》［15］中对常见的矩形单坡屋面、双坡屋面和拱形屋面等结构形式的风荷载体型系数进行了规定，对于复杂形状的大跨屋盖结构则没有给出参考值，因此对大跨屋盖结构的风荷载分布规律进行研究就显得尤为重要.为了具体分析大跨屋盖表面风荷载特性，按照缩尺比1∶250进行了刚性模型风洞测压试验［1-3］，分析屋盖表面风载分布特性.

1 风洞试验概况

1.1 试验模型及流场模拟

模型是按照1∶250缩尺比采用ABS板制成的刚性模型，具有足够的强度和刚度.模型与实物在外形上保持几何相似，高度为14 cm.将模型固定在风洞试验室的转盘上［7-8］，风洞实验模型及周边建筑分布情况如图1（a）所示.为了获得整个结构上的风压分布，在模型屋盖及墙面共布置了347个测点，如图1（c）所示.使用尖劈、挡板、粗糙元作为大气边界层模拟装置在风洞中模拟出符合我国规范要求的缩尺比为1∶250的B类地貌风场，平均风剖面指数α=0.15.测压参考高度H r取15 cm，对应大气边界层风场原型高度为37.5 m.平均风速及湍流度剖面如图2（a）和图2（b）所示，其中U为不同高度处平均风速，U r为参考高度处平均风速，取为7.06 m/s，H为风洞试验高度.为了获得整个屋盖上的风压分布，在模型屋面布置了183个测点，采用电子压力扫描阀EPS进行测压，在0°～360°范围内每间隔15°进行一次风压测量，风向角示意图如图1（b）所示，屋面测点布置图如图1（c）所示.

图1 模型摆放布置及测点布置图

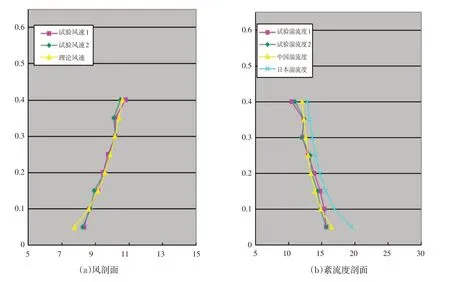
图2 B类风场风剖面及紊流度剖面

1.2 数据处理方法

实验中符号约定以压力向内（压）为正，向外（吸）为负，屋盖表面各测点的风压系数由下列公式给出：

cpi(t)是试验模型上第i个测压孔所在位置的风压系数，pi(t)是该位置上测得的表面风压值，p0、p分别为参考点处测得的平均总压和平均静压.对于双侧受风的位置（内外对应布置两个测压孔），由内外表面对应的测压点测出的压力相减得到：

其中，Δcpi(t)表示试验模型i测点所在位置的风压差系数，pii(t)、poi(t)分别表示该位置内外表面的风压值，为简化叙述，本文采用压力系数cpi(t)来表示公式（1）、（2）两种情况.

净脉动风压均方根Crms可用下式求得：

式中Cpi,k为测点i第k次采样所在位置的合风压系数，N为样本总数.由此可以求出测点的极大值风压系数和极小值风压系数：

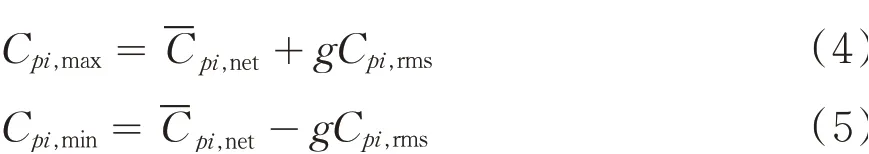
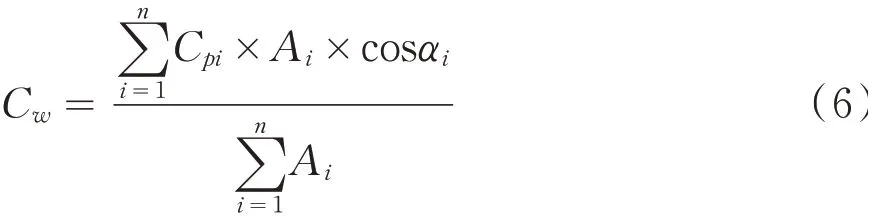
式中：Cpi为测点i处的风压系数，Ai为测点i的代表面积，αi为测点i处外法线与竖直方向的夹角.

2 平均风荷载特征

2.1 平均升力系数随风向角的变化状况

图3为模型屋盖表面平均升力系数随风向角改变的曲线，从图可见，屋盖表面平均升力系数均为负值，可知屋盖表面在各风向角下均受风吸力作用.为了准确地分析屋盖表面不同区域的升力系数，根据本文屋盖表面风荷载分布特性将屋面划分出M（M55、M56、M57、M41）、P（P5、P6、P7）、N（N55、N56、N57、N73）三个负压较大的区域，N区域与P区域最大负压均出现在30°风向角下，最大值分别为-1.884和-1.914，在0°～90°风向角下，N区域位于迎风屋脊，而P区域位于背风屋檐，两者均呈现出先增大后减小再增大的W型变化趋势，这是由于两个区域处于平行位置，来流与锐利边缘形成的夹角相近，两者气流分离、再附的作用形式相似，故随风向角变化趋势也基本一致.M区域位于屋角处0°～30°风向角下平均升力系数变化不明显，这是由于模型摆放（如图1所示）本身与来流存在一定夹角，模型旋转超过30°后，M区域屋角才开始正对来流，气流分离作用增强，M区域负压开始逐渐增大，在180°风向角前呈现出先增大后减小的趋势，在75°达到最大值-1.897后开始逐渐减小.屋盖表面平均升力系数随风向角增加呈现先增大后减小再增大再减小的W型趋势，在30°时达到最大值1.27，但总体变化较为平缓.角度在180°后一号展馆来流方向被周边建筑遮挡，使角度在180°～315°之间升力系数明显减小.屋盖整体平均升力系数在180°时取的最小值为-1.07（后续所述升力系数均为绝对值）.

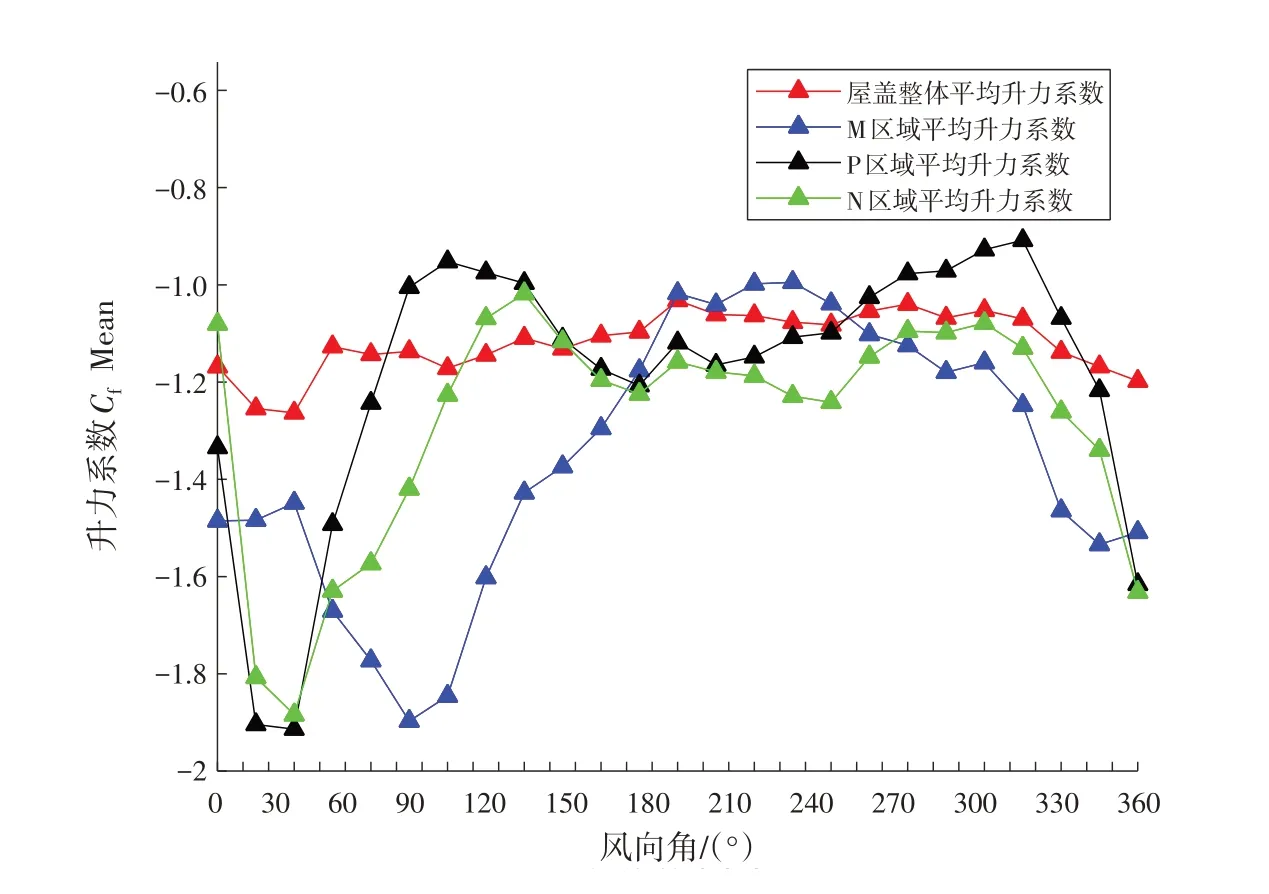
图3 屋盖表面平均升力系数随风向角变化曲线

2.2 平均风压系数分布特征

选取0°、45°、90°三种典型风向角下屋盖表面平均风压系数进行分析，由图4（a）可知，在0°风向角下屋面均受风吸力影响，且在迎风屋檐处发生气流分离产生较大负压，并在屋脊处产生二次分离，使屋脊两侧产生高负压区，最大负压区出现在上游屋脊下侧、下游屋檐边缘及屋角处，由于模型并非水平放置，并与来流存在一定夹角.故0°风向角下模型本身摆放存在斜角，导致屋角处平均风压系数变大，最大平均风压系数为-1.8.背风屋檐由于受尾流影响，且模型的矢高比（R/S）较大，故受尾流影响较为明显，出现了高负压区域其最大值为-1.8，而屋面大部分区域平均风压系数介于-1.3～-1.1之间.

由图4（b）可知，当来流以一定斜角流向建筑时，风在屋面上将产生一个沿分离线的速度分量，形成两个锥形涡，在迎风屋角产生局部强负压，最大风压系数达-1.7，超过周边区域风压系数26%～30%，风在屋面右下部分屋脊处发生二次分离，在分离部分产生较强负压，最大风压系数达-1.5，超过周边区域风压系数13%～20%，与0°风向角相同的在来流下游区域屋檐处产生较强负压；由图4（c）可知，在90°风向角下屋面风压系数分布呈规则的阶梯状，来流在屋檐处发生流动分离并在边缘产生高负压区域，最大平均风压系数为-1.8，而屋面大部分区域平均风压系数均介于-1.2～-1.1之间，分布较为均匀.

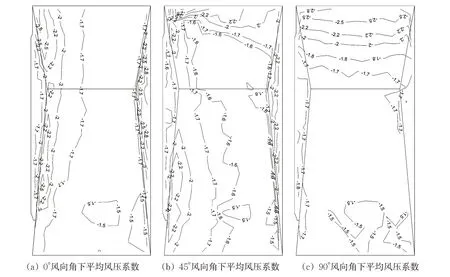
图4 屋盖平均风压系数分布云图

典型测立风压系数随风向角度变化如图5所示.屋盖角部最大负风压系数（M57、M56）分别出现在15°和60°风向角时，值得注意的是15°风向角下下游屋缘处的P区域与屋脊处的N区域典型测点同样达到最大负风压.

图5 典型测点风压系数随风向角变化图

3 脉动风荷载特征

3.1 脉动升力系数随风向角的变化

会展中心屋盖表面脉动升力系数均方根系数随风向角变化的曲线图，如图6所示.由图可知P区域和N区域在0°～180°风向角下随着风向角的增大其脉动升力系数大致上呈递减趋势，在45°风向角下出现一个较为明显的回升.M区域的变化曲线呈先减小后增加再减小的趋势，脉动升力均方根系数最大值在75°风向角时出现，其值为0.3221.在0°～180°之间屋盖整体表面脉动升力系数均方根系数呈现出先增大后减小，再增大再减小的趋势.在45°风向角下屋盖表面脉动升力系数均方根取得最大值为0.184，在165°风向角下取得最小值0.147.

图6 屋盖表面脉动升力系数随风向角变化曲线图

3.2 脉动风压均方根系数分布特征

选取0°、45°、90°三种典型风向角的脉动风压均方根系数分布特征进行分析，如图7所示.由图7（a）可知，在0°风向角下，迎风角部风压系数均方根系数介于0.24～0.26之间，而中心区域则介于0.14～0.16之间，表明迎风角部区域气流脉动较为强烈.而屋盖东南处出现了的较大脉动风压均方根系数分布，这是由于气流在迎风屋檐发生分离后，在东南处屋脊处出现二次分离，引发较强烈的气体流动分离所致.在背风面屋檐处出现脉动风压均方根系数最大值0.34，这是由于北侧屋盖处于来流下游位置，而气流在上游屋盖角部和屋脊等锐利边缘发生强烈的气流分离，产生自由剪切层并朝着尾流方向卷起来形成集中的涡，然后向下游脱落，导致下游气流脉动更为剧烈.

由图7（b）可知，在45°风向角下，来流在屋盖西南角部发生分离并形成锥形涡.与0°风向角相似，迎风屋檐与屋角处脉动风压均方根系数较大，尤其是屋角处的脉动风压均方根系数最大值达到0.34，而靠近屋盖中下游部分的脉动风压均方根系数则在0.14～0.18之间，在来流下游屋檐处同样出现较大值，但该处脉动风压均方根系数小于0°风向角下时的值，这是由于当来流趋向水平于模型时与锐利边缘的夹角减小，使得锐利边缘对气流阻碍降低，气流分离得并不强烈，屋盖自西向东较为平缓，气流可以顺畅地通过，因此45°风向角时下游屋檐脉动风压较0°风向角时要小.

如图7（c）所示，在90°风向角下，来流水平于屋盖，以短轴为界，西侧屋盖的脉动风压系数均方根显著大于东侧屋盖，靠近西侧外缘处大部分区域净脉动风压均方根系数较大，其值介于0.20～0.28之间，而处于来流下游的东侧屋盖则介于0.14～0.18之间.脉动风压均方根系数分布呈现出规律的阶梯式递减，这是由于在迎风面的屋檐处发生较为强烈的流动分离，使得分离处风压脉动较大，且下游几乎没有锐利边缘，屋盖自西向东气流可以顺畅通行，因而脉动较小.脉动风压均方根系数呈现出递减的趋势.

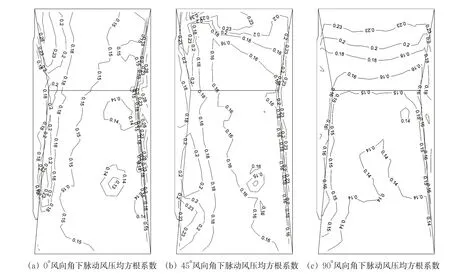
图7 屋盖脉动风压均方根系数分布云图

如图8所示，对比平均风压系数随风向角变化趋势可以看出，平均风压系数大的地方脉动风压系数也大，测点M56在45°风向角下取的屋盖全风向角下最大脉动风压系数，同时可以看出N区域（屋脊处）的脉动风压系数浮动并不明显，说明该处的脉动风压随风向角变化影响并不大，P区域（下游屋缘处）在0°风向角下取的最大脉动风压，除45°风向角下有个增幅外，脉动风压系数均方根整体随风向角增大而减小，M和N区域均在45°风向角取的最大值，并且P区域在此时脉动风压系数也在增大，因此，从图8可以得出45°风向角为最不利风向角的结论.

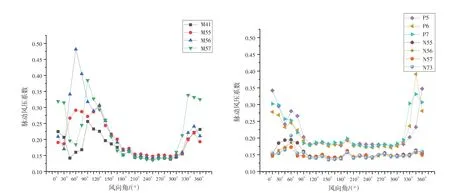
图8 脉动风压均方根系数随风向角变化图

4 极值风荷载特征

通过实验数据分析可知会展中心屋盖受风吸力影响远大于向下的风压力，故本文仅分析极小值风荷载分布情况，分别取0°、45°、90°三个典型风向角进行分析.

4.1 极小值升力系数随风向角变化

图9为会展中心屋盖表面极小值升力系数随风向角变化曲线图.由图可知，屋盖表面极小值升力系数随风向角变化趋势与前文所述平均升力系数和脉动升力均方根系数的变化规律相同.在0°～180°风向角下P区域和N区域极小值升力系数呈先增大后减小的趋势，P区域极小值升力系数最大值出现在15°，其值为-2.937，N区域极小值升力系数最大值出现在30°，其值为-2.763.与P、N区域不同的是M区域极小值升力系数自30°风向角开始增大，到75°时风向角开始减小，最大值出现在75°风向角时，其值为-3.025.在0°～90°风向角下，屋盖整体极小值平均升力系数随风角呈现出先增大后减小的趋势，最大值-1.85出现在-15°～30°时.在90°～195°风向角下呈现出减小趋势，195°～360°呈现出先增大后减小再增大再减小的趋势，270°出现最小值-1.57，在300°～360°风向角下，极小值升力系数快速增大.

图9 屋盖表面极小值升力系数随风向角变化曲线

4.2 极小值风压系数分布特征

由式（5）可知，极小值升力系数可经过净脉动风压均方根系数计算得到，此处选取0°、45°、90°三种典型风向角下极小值风压系数分布特征进行分析.

图10为三种风向角下屋盖表面极小值风压系数分布云图.由图10（a）可知，在0°风向下，屋盖西南角部与北侧屋檐处极小值风压系数为-2.8，屋盖中心区域的极小值风压系数介于-1.8～-1.6之间，整体规律与平均风压系数分布规律类似.气流迎风面角部产生较强的气流分离，气流在迎风屋檐发生分离后，在东南处屋脊处出现二次分离，引发较强烈的气体流动分离.在背风面屋檐处出现脉动风压均方根系数最大值为-2.8，这是由于北侧屋盖处于来流下游位置，而气流在上游屋盖角部和屋脊等锐利边缘发生强烈的气流分离，产生由剪切层朝着尾流方向卷起形成集中的涡，然后向下游脱落，因此极小值风压系数绝对值较大.

由图10（b）可知，在45°风向角下，来流在屋盖迎风角部发生气流分离并形成锥形涡.与45°脉动风压系数均方根系数相似，迎风屋檐与屋角处极小值风压系数绝对值较大，尤其是迎风面屋角处的最大值达到-0.28，而靠近屋盖中下游部分则在-0.18～-0.16之间，在来流下游屋檐处同样出现极小值绝对值较大的区域，这是由于当来流趋向于90°吹向模型时，锐利边缘对气流分离的强度降低，屋盖自西向东较为平缓，气流可顺畅地通过，因此脉动强度较小.

图10 屋盖极小值风压系数分布云图

如图10（c）所示，在90°风向角下，极小值风压系数分布呈现出规律的阶梯式递减，这是由于在迎风面的屋檐处发生较为强烈的流动分离，且下游几乎没有锐利边缘，屋盖气流自西向东可以顺畅通行，与脉动风压均方根系数呈现出相同的规律.

5 结论

通过对会展中心屋盖刚性模型风洞测压试验，研究了屋盖表面整体升力系数随风向角变化的规律及不同风向角下风压系数分布特征，得出如下结论：

（1）全风向角下，屋盖表面均受风吸力作用且平均、脉动、极小值升力系数随风向角变化趋势一致.

（2）迎风屋檐及屋角处气流分离现象较强，来流下游屋檐受再附剪切层和旋涡的影响，负压同样较强.净极小值风压系数与净脉动风压均方根系数分布规律一致，迎风屋檐、屋角及来流下游屋檐处净极小值风压系数绝对值大于屋盖其他区域.

（3）在迎风面屋檐、屋角及屋盖表面的锐利边缘处气流分离较强，风压脉动较其他区域更为强烈，屋盖东南角屋脊处气流发生二次分离，导致屋脊下游风压脉动增强，净极小值风压系数绝对值也较屋盖中心区域更大.

（4）风向角变化对风荷载分布的影响显著，不同风向角下的气流分离区域和漩涡脱落作用存在差异，平均风压系数的最大值出现的区域也随风向角的变化发生改变，在设计时应注意考虑最不利风向角对屋面荷载分布的影响.

（5）在工程实践中，考虑屋盖表面风压分布特性和高矢跨比时背风屋檐受尾流和再附剪切层影响较为明显，对类似会展中心模型的屋盖，应该对靠周边建筑外侧部分的屋檐、屋角及屋脊下游处屋盖进行强化处理，增强其刚度，减小因风载造成的结构振动，且背风屋檐处也需加强，避免其因遭受较大负压而破坏.