框架效应对预应力混凝土箱梁桥顶板横向预应力储备的影响分析

戴志成，钟新谷，赵 超

（湖南科技大学 结构抗风与振动湖南省重点实验室，湘潭411201）

0 引言

近年来，预应力混凝土变截面箱梁桥顶板普遍存在纵向开裂的现象［1-2］，严重影响箱梁桥的耐久性和安全运营等［3-5］.有研究者认为，箱梁桥顶板纵向开裂主要是由于没有设置横向预应力筋或者是由于车辆超载、热梯度、横隔板设置不当等因素造成的［6-9］，文献［9］提出箱梁桥的框架效应是导致顶板在上述因素下产生纵向裂缝的重要原因.文献［10］［11］提出箱梁框架效应会导致顶板横向预应力储备降低，产生顶板纵向裂缝，但其没有明确箱梁参数对框架效应的影响.文献［12］并未明确规定箱梁的横向内力计算方法，且其横向内力计算主要依据是T型梁桥桥面板的计算规定，显然没有考虑箱梁的特点.建立箱梁横向框架效应数值模型，采用FORTRN语言编程专用程序可计算得出任意截面的横向应力，但其过程较为复杂没有得到广泛应用，同时分析框架效应对横向预应力的影响困难［13-14］.文献［15］基于有限元法提出影响预应力混凝土箱梁顶板横向预应力框架效应的参数主要有底、顶板厚度之比、顶板与腹板厚度之比和箱梁高度与宽度之比，但未指出框架效应对顶板横向预应力的影响.本文基于ANSYS数值模拟与现场实测的结合，对横向预应力筋、横隔板布置和箱梁参数进行数值模拟，研究框架效应对预应力混凝土箱梁横向预应力的影响及随箱梁截面几何参数的变化规律，对防止预应力混凝土箱梁桥顶板的纵向开裂及工程设计有重要的参考意义.

1 横向框架数值模型

1.1 工程背景

湖南省汝郴高速公路黄家垄特大桥为单箱单室变截面预应力混凝土连续刚构箱梁桥，其主桥部分长度为45 m+5×80 m+45 m，箱梁墩顶梁高5.0 m，最大悬臂长40 m，底板宽度为6.5 m，顶板厚度均为0.28 m，底板厚度由墩顶0.7 m按2.0次抛物线渐变到跨中0.28 m；顶板悬臂长2.75 m，厚度由端部0.2 m变到根部0.8 m，顶板中心厚0.28 m；腹板厚度由端部0.7 m变到跨中0.4 m；墩顶设4道0.7 m厚的横隔板，过度墩主桥设1.2 m厚的横隔板，主跨跨中设置1道0.4 m厚的跨中横隔板；预应力筋采用三种线形布置，A类为折线型，B类为直线形，C类与A类线形一致方向相反，沿箱梁轴向每0.5 m布置一根，三者交替布置，预应力筋线形如图1所示.

图1 预应力筋布置图

1.2 模型建构

截取黄家垄特大桥主跨梁段建立三维实体模型，以三维实体单元模拟混凝土材料，桁架单元模拟横向预应力钢绞线，内嵌作用模拟混凝土与预应力钢筋的相互作用，边界条件为两端固结.梁体混凝土采用C55，预应力钢绞线采用φs15.2高强低松弛预应力钢绞线，单根预应力张拉为164.8 kN，弹模量为E=1.95×105MPa，标准抗拉强度fpk=1860MPa，张拉控制应力σcom=0.75fpk，抗拉强度设计值fpk=1260MPa；泊松比、膨胀系数等材料参数均参照文献［12］选取.在ANSYS中模拟预应力的方法大致有三种：等效降温法、初应变法和非线性弹簧法.本文采用等效降温法模拟预应力加载［16］，也是常用方法之一.为了保证网格是有足够的精度和规则的单元形状，在自动生成的基础上，对大部分的模块都进行了人工干预，网格大小是200 mm×200 mm，如图2所示.

图2 模型网格划分图

1.3 计算结果分析

无框效应顶板中心预应力效应的计算可简化为文献［12］中6.1.5节的公式式中σ为顶板中心轴处压应力，I为截面惯性矩约等于0.0038 m4，y为截面计算纤维处至截面中心轴的距离，取1/2板厚为0.14 m，F为横向预应力筋有效张拉合力等于494.4 kN，A为换算截面面积等于0.225 m2，e为张拉力对截面中心的偏心距，e=0.06±0.01m.现场发现由于存在施工误差，横向预应力管道所在位置会偏离设计值1 cm左右.设计图纸给出的波纹管中心距箱梁中心轴相差0.6 cm，e=6±1cm，如图3所示，将相关数值带入上式可得σ上=-1.104±0.182MPa、σ中=-2.197MPa、σ下=-3.29±0.182MPa.

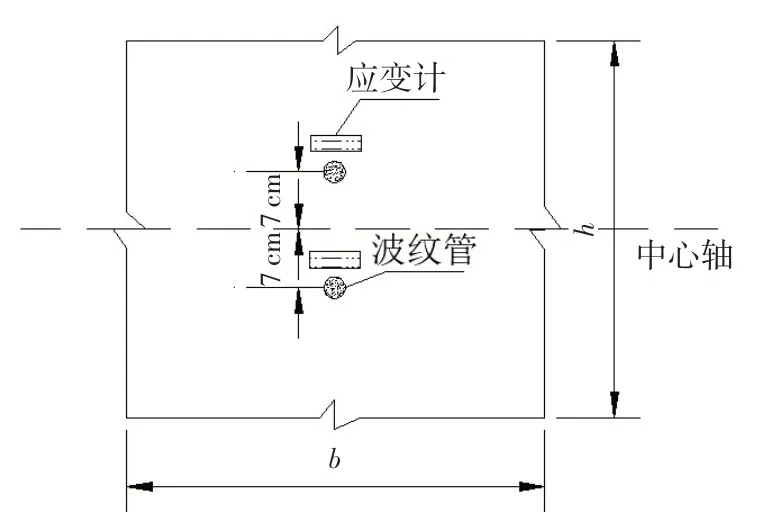
图3 截面偏心示意图

如图4所示支座横隔板处的横向预应力为零，随远离支座横隔板处横向预应力逐渐增加，当距离达到8 m左右基本稳定；但至跨中横隔板中心左右4 m横向预应力减小，减小的最大幅度约为30%.横向预应力稳定区域，按文献［12］中6.1.5节的公式：计算的无框架效应计算值与数值模拟结果相差40%左右，显然图4所示的横向预应力分布规律需要通过实测进一步证实.

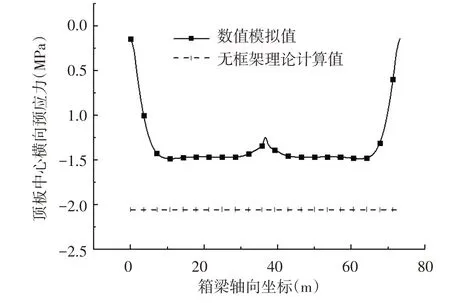
图4 数值模拟与无框架理论计算对比图

2 现场实测方案

为验证数值分析的可靠性，在黄家垄大桥的1#～7#块顶板横向安置应变计.应变计布置在顶板横向预应力钢筋中心点的正上方，绑扎在顶板钢筋上如图5所示，以便在1#～7#块浇筑、预应力张拉完成后，实测出顶板中心的横向预应力.预应力效应测量为钢弦应变计（自带温度补偿），在横向预应力钢筋张拉后，考虑混凝土传力的时间效应，每间隔1 h测量一次，直至测试的数值基本稳定后，此时的测试数值作为横向预应力效应值.

图5 应变计布置图

如图6所示：支座横隔板处的横向预应力出现拉应力，范围和数值很小，随远离支座横隔板处横向预应力逐渐增加，当距离达到5 m左右时基本稳定，但随即出现了跳跃.黄家垄特大桥主跨横向预应力筋采用三种线形布置，A类为折线型，B类为直线形，C类与A类线形一致，方向相反，图6标示了B类预应力筋（直线形，e=7cm）和A、C类预应力筋（折线形，e=-7cm）的无框架理论计算值.实测值出现了跳跃，显然与横向预应力筋采用三种线形布置相关，但实测值总体上更接近偏心距e=0的无框架理论计算值，实测值远大于B类预应力筋（e=7cm）计算值，小于A、C类预应力筋（折线形，e=-7cm）计算值，表明实际偏心距与设计存在偏差，横向预应力筋基本布置在顶板中线，即偏心距接近为零.

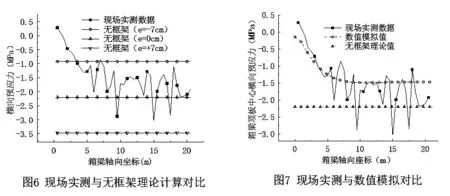
图6 现场实测与无框架理论计算对比图

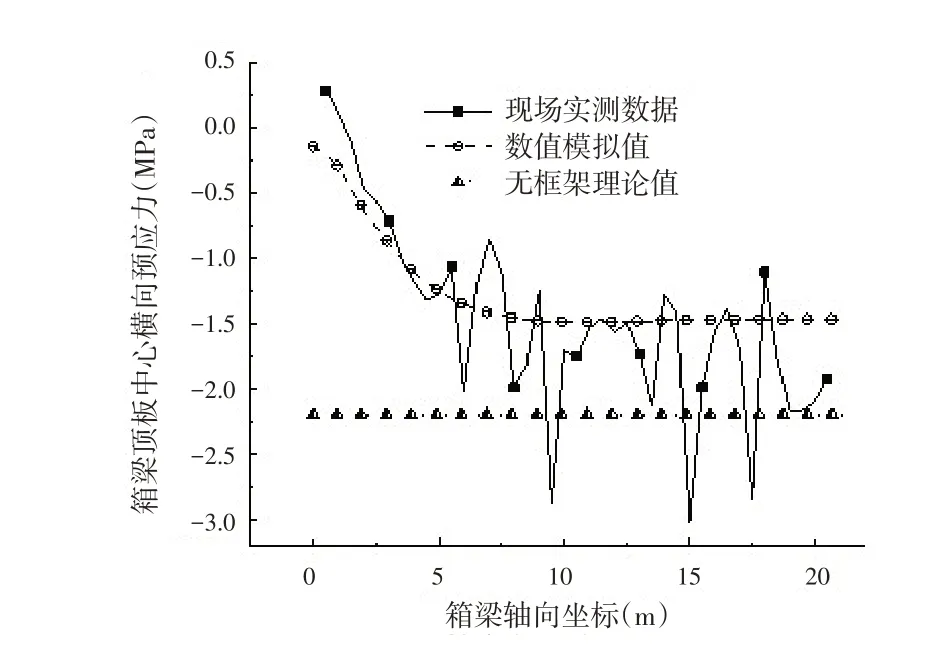
图7 现场实测与数值模拟对比图

如图7所示现场实测数据与数值模拟结果数值显示，模拟值的变化趋势与实测数据基本一致，整体讲实测值小于数值分析值.

3 箱梁截面几何参数敏感性分析

为分析箱梁参数变化对框架效应的影响，与图2类似.本文用ANSYS建立了66座数值模型进行分析，预应力筋的配置与黄家垅大桥一致.研究箱梁桥在不同高跨比、宽跨比、底板与腹板厚度比、腹板厚度与顶板宽度比对预应力混凝土箱梁桥顶板下缘压应力储备影响的变化规律.

（1）宽跨比：图8保持腹板、底板及顶板厚度不变，研究不同宽跨比k/l下对横向预应力储备的影响，取宽跨比m=k/l为0.30、0.25、0.20和0.15分别计算，表明宽跨比k/l越大箱梁顶板下缘中心横向预应力储备越大，且随着箱梁长度的增加，增加趋势越明显，在同一宽跨比下，随着箱梁长度l增加，顶板下缘压应力σ储备不断增加，但增加趋势缓慢；在0.15≤m≤0.30内，顶板下缘压应力σ随着m的增大而增大.

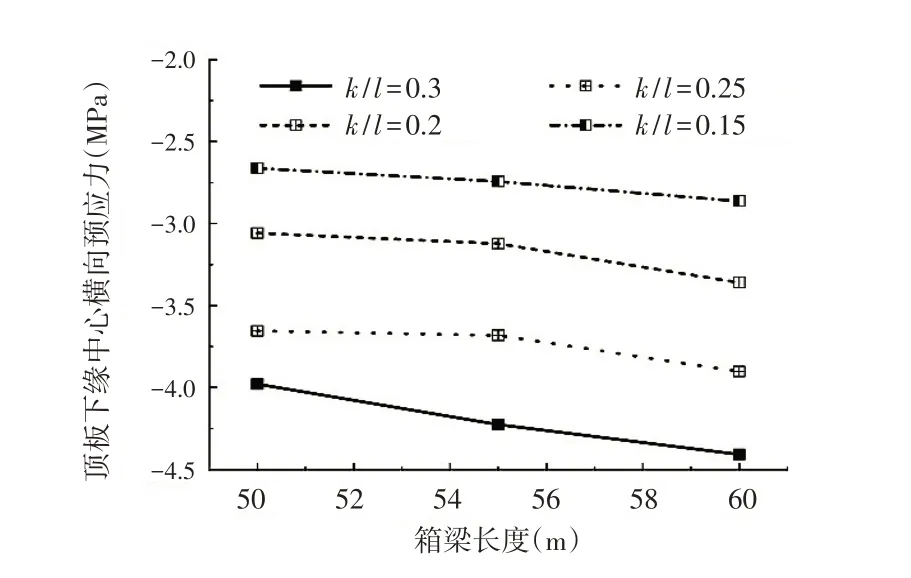
图8 宽跨比影响图

（2）底板与腹板厚度之比：图9保持顶板宽度、厚度不变及箱梁长度不变，研究横向预应力在底板与腹板厚度之比t/f的作用效应，取底板与腹板厚度比p=t/f为1.2、1.0、0.8、0.6和0.5分别计算，底板与腹板厚度之比t/f越大箱梁下缘中心横向预应力储备越大，随着腹板厚度的增加，预应力储备增加趋势越明显.在0.50≤p≤1.2内，顶板下缘压应力σ随着p的增大而增大；当f≤0.6m时，增长趋势缓慢.

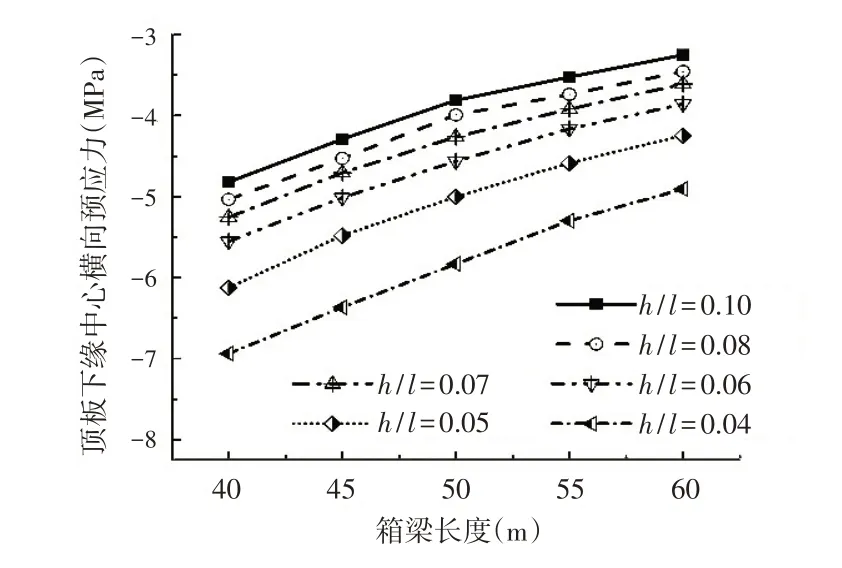
图9 底板与腹板厚度之比影响图

（3）高跨比：图10保持腹板、底板厚度不变及箱梁宽度和顶板厚度不变，研究不同高跨比h/l下对横向预应力储备的影响，取高跨比n=h/l为0.10、0.08、0.07、0.06、0.05和0.04分别计算，高跨比h/l越小箱梁顶板下缘中心横向预应力储备越大，且箱梁长度越短增长趋势越明显，在同一高跨比下，随着箱梁长度l增加，顶板下缘压应力σ储备不断减小，且减小趋势明显；在0.04≤n≤0.10以内顶板下缘压应力σ随着n的减小而增大.文献［17］指出，随着设计和施工技术的进步，连续刚构箱梁桥根部的n一般为l/15.7～1/20.6.而在这一区间内，n越小顶板下缘压应力储备越大.

图10 高跨比影响图

（4）腹板厚度与顶板宽度之比：图11保持箱梁底板、顶板厚度不变及箱梁长度不变，研究不同腹板厚度与顶板宽度之比f/k对横向预应力储备影响，取底板与顶板宽度之比q=f/k为0.040、0.035和0.030分别计算，腹板厚度与顶板宽度之比f/k越大箱梁下缘中心横向预应力储备越大，随着顶板宽度的增加，预应力的储备也明显增加；在0.030≤p≤0.040内，顶板下缘压应力σ随着q的增大而增大，且增长趋势明显，表明框架效应随着顶板宽度的增加而减弱.

综合分析上述四幅图可知，腹板宽度对横向框架效应影响最大，预应力混凝土箱梁桥在设计时特别要注意腹板厚度的设计，并注意腹板与其他参数之间的比例.

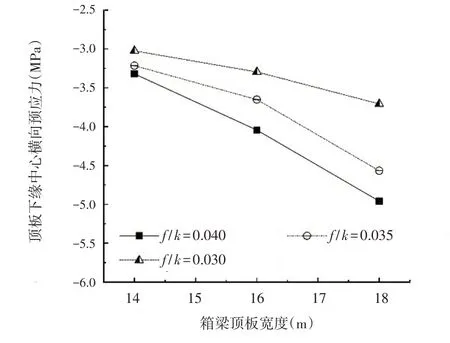
图11 腹板厚度与顶板宽度之比影响图

4 结论

（1）由现场实测数据和数值模拟结果表明，墩顶、跨中横隔板处出现纵向裂缝的可能性较大，表明预应力混凝土箱梁桥墩顶外由于横隔梁刚度大，在其5 m左右范围内横向框架效应影响显著，应按非预应力混凝土设计预防顶板纵向裂缝产生，在跨中设计的横隔板附近应增加纵向抗裂钢筋.

（2）通过分析箱梁各参数之比对预应力混凝土箱梁桥顶板横向预应力储备的影响可得出，增加宽跨比、底板与腹板厚度之比、腹板与顶板宽度之比以及减少高跨比将在一定程度上增大预应力混凝土顶板横向有效预应力，为预应力混凝土箱梁桥参数的设计提供参考依据.

（3）减少预应力混凝土箱梁桥顶板纵向裂缝，需要在本文的基础上进一步明确箱梁桥受其他作用下对顶板横向有效预应力的影响.建议修改相关规范时，明确框架效应对预应力混凝土箱梁桥的横向预应力筋的设计方法.