弹头形状对侵彻多层靶弹道的影响

李鹏飞，吕永柱，周 涛，肖 川，宋 浦

（1. 西安近代化学研究所，陕西 西安 710065；2. 中国兵器科学研究院，北京 100089）

1 引言

自侵彻弹在海湾战争中应用以来，对洞穴、工事、建筑目标表现出优异的毁伤能力。侵彻弹已经成为各国争相发展的常规打击武器。在侵彻弹打击大型建筑目标时，弹体逐层侵彻多层混凝土靶，属于非正侵彻，常伴随着一定的弹道和弹体姿态的偏转，随着层数增加偏转更加剧烈，对弹体力学响应、装药安定性影响严重，因此对多层靶斜侵彻过程的弹体姿态偏转研究尤为重要。尹放林等［1］基于弹靶分离的思想，采用微分面力方法推导了侵彻弹道平面运动的方程，对岩石侵彻的弹道轨迹进行了预测。Chen［2］对混凝土斜侵彻问题展开过理论研究，建立了斜侵彻混凝土薄靶时弹道偏转角的理论公式。孔祥振［3］，薛建锋等［4］基于弹性-损伤-塑性响应分区模型构造了靶自由表面衰减函数，对法向半经验法向阻力函数修正，得到靶体倾斜角、弹体速度对侵彻深度和偏转角的影响趋势。高旭东［5］、吴普磊等［6］基于刚性弹假设和混凝土侵彻运动模型研究了一定着角、小攻角条件对侵彻弹道偏转的影响规律。针对弹体斜侵入靶体的过程，文献［7］通过引入一个阻力不对称系数Kc，减小弹体一侧表面的阻力从而引起弹体姿态偏转。其他许多学者对弹体侵彻混凝土理论模型和机理进行了较为深入研究［8-12］，但是，由于力学模型目前仍较为缺乏，所以关于弹形对侵彻多层靶弹道影响研究的相关文献较少。

为此，本研究针对侵彻弹斜侵彻多层混凝土靶过程弹体姿态偏转问题，提出了头部刻槽形弹体结构设计，基于LS-DYNA 软件数值模拟计算，分析不同攻角条件下尖卵形弹体和刻槽形弹体侵彻单层薄靶姿态角变化规律，同时开展了两种弹体侵彻10 层混凝土靶的试验，通过对比两种弹形头部形状对弹道偏转的影响，以期为弹道稳定的弹形设计提供参考。

2 侵彻弹结构设计

分别设计尖卵形和头部刻槽形两种侵彻弹体结构，如图1 和图2 所示。两种侵彻弹的外径均为125 mm，长度均为742 mm，壁厚均为12.5 mm。尖卵形弹体头部曲径比为2.5，弹体质量34.2 kg，装药质量约为8.5 kg。刻槽形弹体结构是在尖卵形弹体结构基础上，距前端40 mm 处增加直径为87 mm 台阶，圆周上对台阶进行均布刻槽，每个刻槽夹角为30°，其它结构与尖卵形弹体一致，弹体重量34.5 kg，装药重量与尖卵形弹体一致。刻槽形弹体结构的设计思路是通过改变局部碰撞力的大小和方向，平衡弹体头部碰撞靶板过程的偏转作用。图中刻槽形弹体结构台阶面与靶体碰撞可产生平行于弹轴向的作用力，对突起的台阶进行刻槽，起到排混凝土碎屑作用，通过剩余台阶面宽度控制碰撞作用力的大小。

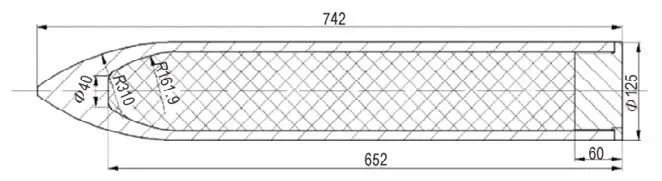
图1 尖卵形弹体结构Fig.1 Structure of ogive-nosed projectile

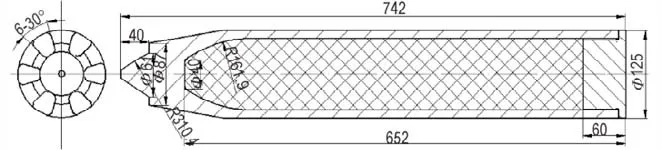
图2 刻槽形弹体结构Fig.2 Structure of grooved projectile

3 计算模型建立

采用LS-DYNA 软件进行数值模拟分析，对比尖卵形弹体结构和头部刻槽形弹体结构侵彻多层混凝土薄靶过程的姿态和弹道特性。为简化计算，构建二分之一有限元模型，战斗部壳体、装药与靶板材料均采用拉格朗日网格离散，装药与壳体之间定义自动面-面接触算法，壳体与靶板之间定义侵蚀算法。在弹体模型二分之一对称面施加对称约束边界，图3 所示为弹体计算模型。

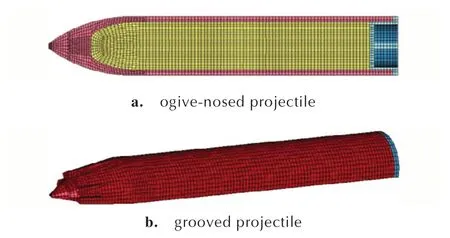
图3 弹体计算模型Fig.3 Numerical calculation model of projectile

装药与壳体材料均采用随动硬化模型*MAT_PLASTIC_KINEMATIC 描述，其应变率效应用Cowper-Symonds 模型来考虑［13］，用与应变率有关的因数表示屈服应力，其表达形式为：

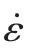
式中，E 为弹性模量，Etan为等效应力-等效应变在塑性阶段的斜率。

战斗部壳体与装药材料模型参数见表1［14］。

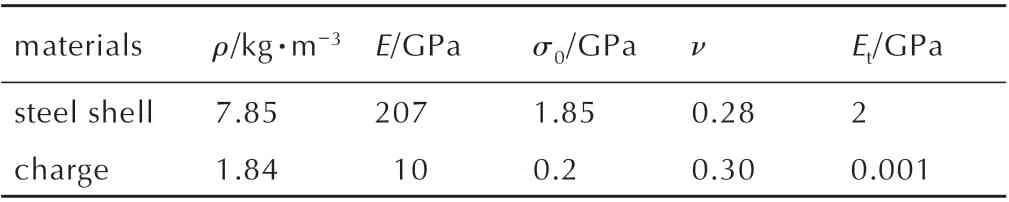
表1 壳体与装药材料参数［14］Table 1 Parameters of shell and charge materials［14］

混凝土材料选用HJC材料动态模型［15］。模型考虑了大应变，高应变率和高压情况，同时结合损伤理论考虑了材料的拉伸脆断行为。作为一种有孔隙的材料，还考虑了材料压溃后的体积压缩量与压力的函数关系。对于HJC混凝土模型，分三段处理：第一段：p≤pc是弹性区。pc及ηc是单轴压力压缩实验中测到的最终压力和应变，弹性体积模量Ke= pc/ηc；第二段pc≤p ≤pe为过渡区，在该区段内混凝土发生弹性应变时其中的气隙被逐步压实，当压力达到pe时材料中的气隙被完全消除；第三段p ≥pe代表被完全压实的介质，其关系式为：

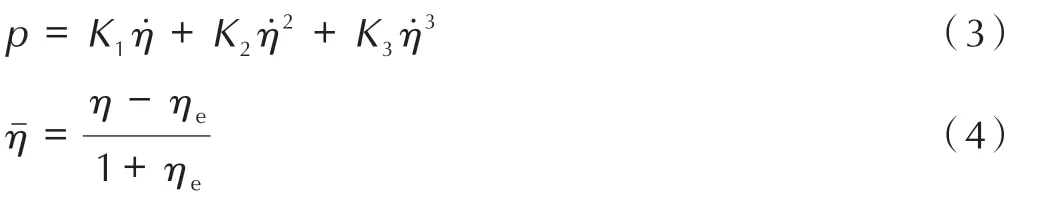
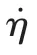
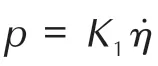
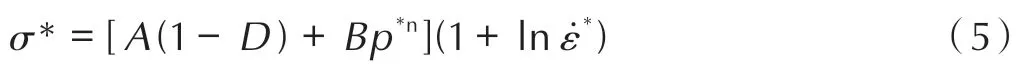
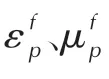
计算中，等效塑性应变ε 和损伤度D 被作为单元是否出现材料失效的双门开关，物理上表示当单元的塑性变形积累至某一阈值时或损伤发展累积到某一阈值时，材料发生破坏从而失去强度。混凝土材料参数见表2［16］。

表2 混凝土材料参数［16］Table 2 Concrete material parameters［16］

4 不同条件下的侵彻弹道偏转

4.1 初始0 攻角侵彻单层混凝土薄靶

应用模型计算两种弹形弹体穿透单层混凝土靶过程，分析弹体受力、姿态偏转和弹道变化。初始时刻弹体运动方向与弹轴重合，弹体速度为700 m·s-1，攻角为0°，弹体轴线沿水平方向向右，靶板与水平方向夹角为80°，混凝土靶厚度为0.1m。计算得到两种弹体头部侵彻单层靶板应力云图，如图4 所示，两图为弹体侵入靶的0.25 ms 时刻，图中显示弹体头部刻槽形弹体结构的台阶部位应力大，达到利用突起台阶调整应力的目的。

计算得到尖卵形弹体穿透靶板后的偏转角角度φ、角速度ω、角加速ω̇度变化曲线，如图5 所示。由图5 可见，在弹体头部入靶板过程，弹体产生正向的偏转角加速度和角速度，弹体有抬头转动的趋势，弹尖出靶阶段角加速度反向，偏转力矩转向，导致角速度由正转为负，弹体产生低头转动的趋势。分析其原因是由于着角的影响，弹靶碰撞作用合力偏离弹轴，产生偏转力矩，导致弹体穿透单层靶后产生一定偏转。

4.2 攻角条件下姿态偏转分析

弹体头贯穿靶板后，弹体具有了一定的角速度，可知在侵彻多层混凝土靶过程中，每层靶前将存在初始的攻角和角速度。弹体侵彻多层靶过程中弹体偏转角度逐渐变化，每层入靶前攻角条件不同，因此，有必要对攻角对不同弹形弹道偏转的影响进行分析。在初始攻角为0°、3°、7°、12°、18°、25°、30°条件下，分别计算得到尖卵形弹体和刻槽形弹体穿透单层靶过程弹体姿态偏转角、角速度、角加速度随时间的变化曲线，如图6 和图7 所示。由图6 和图7 可以看出，两种弹体侵彻单层靶都经历两个阶段，在第一阶段中，弹体姿态偏转角变化幅度大，偏转角速度向峰值递增，角加速度为在正区间，通过侵彻过程分析该阶段对应的是弹体质心以前部分碰撞靶板；第二阶段中，弹体姿态偏转角变化幅度小，偏转角速度由峰值下降，角加速度为在负区间，对应的是弹体质心以后部分碰撞靶板。

图4 数值计算应力云图Fig.4 Stress nephogram of the interaction of projectile and target in numerical calculation

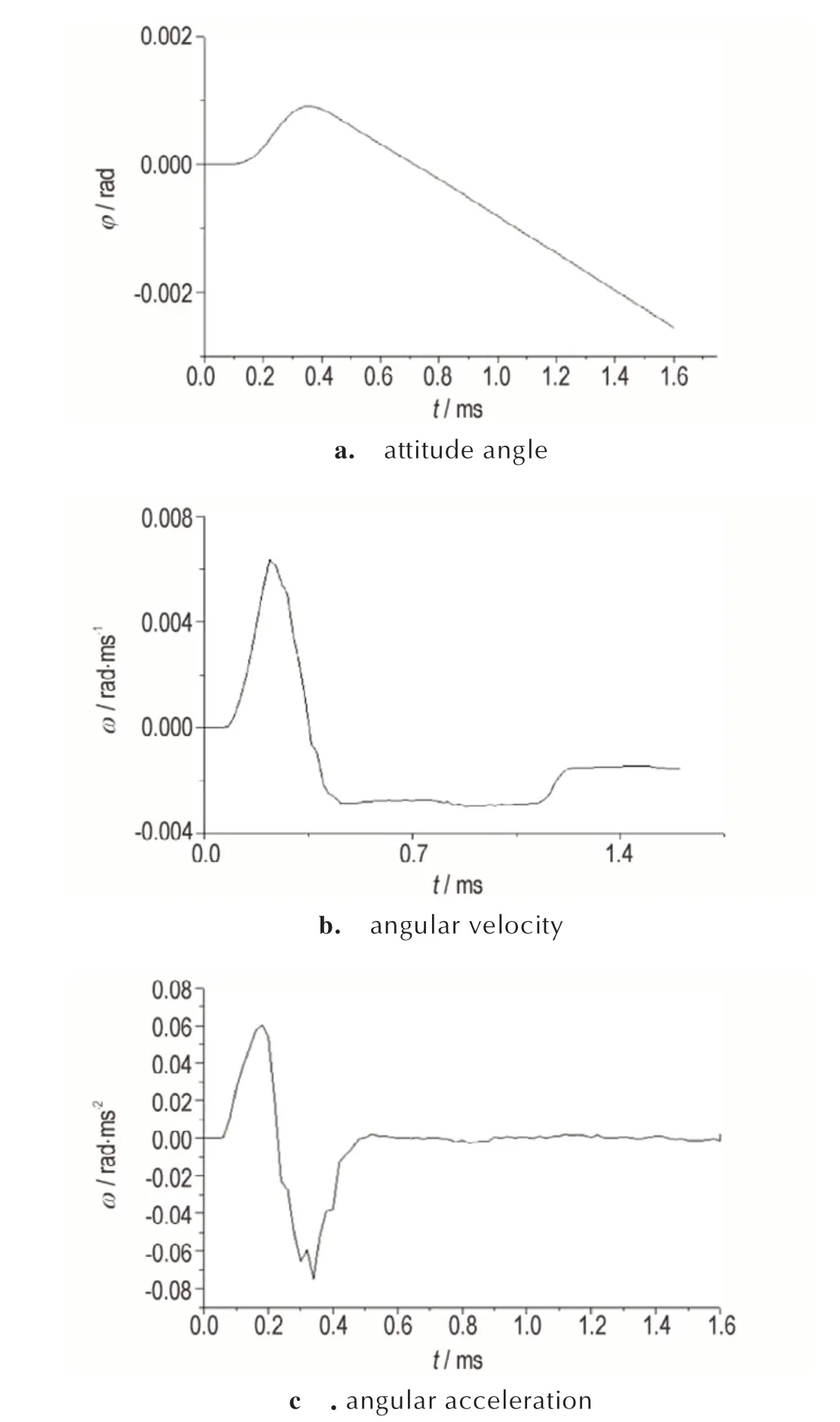
图5 尖卵形弹体侵彻单层靶弹体偏转角度、角速度、角加速度曲线Fig.5 Curves of the relation between the attitude angle，angular velocity，angular acceleration and time of ogive-nosed projectile penetrating single-layer target

在初始攻角为0°、3°、7°、12°、18°、25°、30°条件下，分别计算得到尖卵形弹体和刻槽形弹体穿透单层靶后姿态偏转角、角速度变化，如图8 和图9 所示。由图8 看出，弹体穿透单层靶体后，获得一定角速度增量，当初始攻角小于10°时，角速度随攻角呈近似线性递增；初始攻角大于12°时，尖卵形弹体角速度变化值稳定在一定区间，而刻槽形弹体则呈现下降的趋势。由图9 可以看出，弹体穿出靶体后偏转角度随初始攻角增大而增大，但刻槽形弹体相对尖卵形弹体增大幅度明显趋缓。因此，通过以上侵彻单层靶过程弹体偏转角速度和偏转角角度变化表明，相同的入靶条件下刻槽形弹体侵彻单层过程姿态相对变化较小。

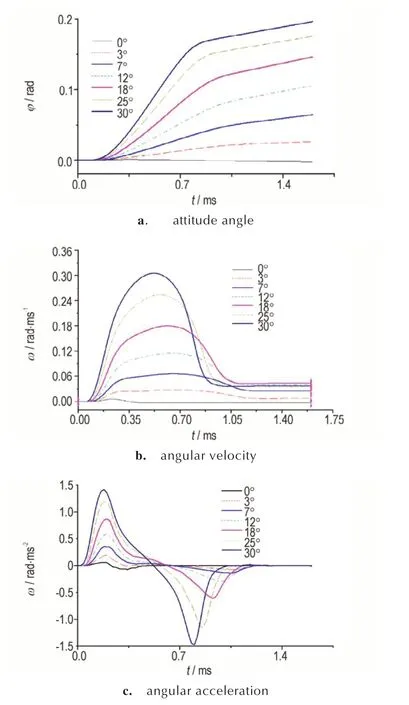
图6 尖卵形弹体不同攻角条件下弹道参数曲线Fig.6 Curves of relationships between ballistic parameter and time of ogive-nosed projectile under different attack angles

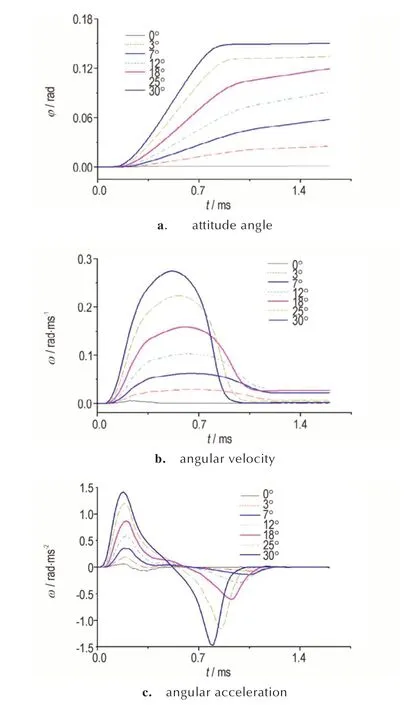
图7 刻槽形弹体不同攻角下弹道参数曲线Fig.7 Curves of relationships between ballistic parameter and time of grooved projectile under different attack angles

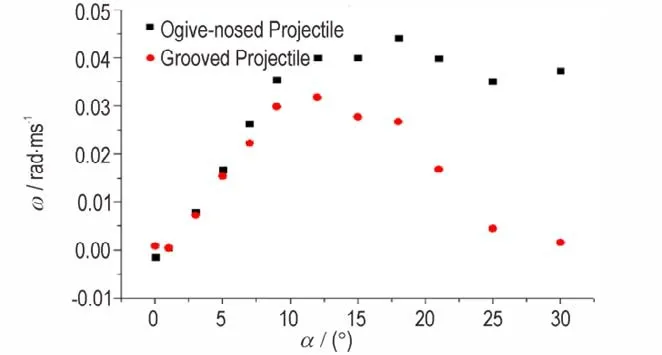
图8 不同攻角条件下偏转角速度Fig.8 Deflected angular velocity of projectile under different attack angles

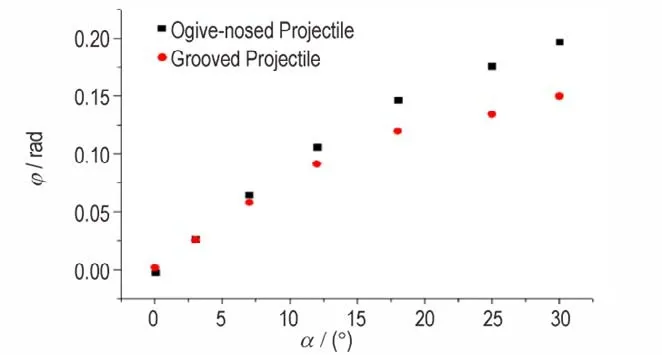
图9 不同攻角条件下偏转角Fig.9 Deflected angle of projectile under different attack angles

5 试验验证及分析

5.1 试验验证

开展了尖卵形弹体和头部刻槽形弹体侵彻10 层混凝土靶试验。混凝土靶板共10 层，首层靶板厚度为0.1 m，其它各层厚度为0.06 m，靶板与水平方向夹角为80°，间距为1 m。混凝土靶体实测平均抗压服强度为42 MPa，配筋率为2%。

试验采用125 mm 火炮发射弹体，布局如图10 所示，炮口在距靶30 m 处水平发射试验弹体。高速摄影仪拍摄试验的全过程，包括靶前飞行段、穿靶过程、靶后飞行段等，获取弹体着靶前、后的速度的姿态角度。

图10 试验布局Fig.10 Experiment setup

5.2 试验结果与分析

利用高速运动分析系统测量出弹体运动速度以及弹轴偏转角度。靶体侧面标记水平标线，弹体轴线方向与水平标线的夹角记为弹体姿态角。以静态标尺作参照，测量出某一时间间隔弹头的位移，根据与实际尺寸的比例系数，得到弹体速度。弹体完全出靶后，确定弹体轴线的方向，标注出轴线与水平标线的夹角α，高速摄影记录如图11 所示。

判读高速录像图像，尖卵形试验弹着靶速度为689 m·s-1，着靶攻角1°，出靶速度为570 m·s-1，刻槽形试验弹着靶速度为685 m·s-1，着靶攻角-0.6°，出靶速度为547 m·s-1。通过沙堆回收了试验弹体，如图12 所示。尖卵形弹体姿态角变化过大，回收过程弹体尾部着地，导致弹体尾部局部破坏。刻槽形弹体穿靶过程姿态变化较小，完整回收弹体，刻槽的前端出现略微侵蚀。通过高速摄影测出每层靶后弹体姿态角，即弹体轴线与水平方向的夹角，其弹体抬头为姿态角为正，低头姿态角为负。统计得到试验中各层靶后弹体姿态角，与相应的数值计算值，见表3。以层数为单位，获得两种弹体侵彻10层靶角度变化曲线，如图13所示。

图11 试验高速摄影图Fig.11 High-speed Photography of Experiment

图12 回收弹体Fig.12 Recovered projectile

表3 试验中弹体穿靶数据Table 3 Projectile Penetration data of projectile in the test

由图13 可见，两种弹体穿透10 层靶后，弹体姿态都发生一定的偏转。尖卵形弹体正向偏转，刻槽形弹体负向偏转。两种弹体穿靶过程中姿态变化具有共同特点，初始姿态变化平缓，随着侵彻层数增加，姿态变化愈加剧烈。分析其原因，主要是由于每层穿靶都给弹体增加一定的偏转角度和角速度，每层逐渐累积，导致随着层数增加姿态角呈指数级增大。通过尖卵形弹体和刻槽形弹体穿靶过程姿态偏转角绝对值对比，刻槽形弹体相比尖卵形弹体姿态偏转幅度小了78%，表明刻槽形弹体在侵彻多层混凝土靶过程中姿态稳定性较好。试验和数值计算表明，通过改变弹头弧线部分形状改变侵彻过程头部受力，从而达到调整弹体侵彻多层靶弹道的目的。

图13 弹体侵彻10 层靶的姿态偏转角曲线Fig.13 Relationship between the Attitude angle of deflection and the number of target layer of projectile penetrating 10-layer target

对各层靶后弹体姿态角进行误差分析，数值计算和试验值的相对误差见图14，计算误差总体小于20%，计算结果和试验符合较好。分析弹体姿态角误差主要来源于两方面，一方面是高速摄影的测试误差，另一方面是数值计算的误差。高速摄影测试中图像的像素质量会给姿态角测量带来一定误差，误差值相对固定，导致偏转角较小时，测量相对误差会较大，这是图中刻槽形弹体误差较大的原因。碰撞过程的数值模型会存在一定误差，每经历一次弹靶碰撞过程，计算误差会累计，导致计算误差逐渐增大。

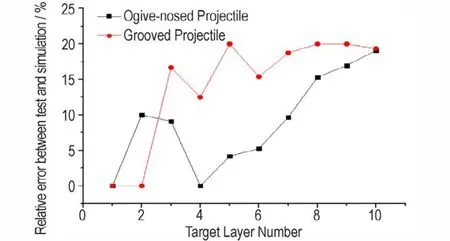
图14 数值计算与试验的姿态偏转角误差对比Fig.14 Comparison of the relative error of attitude angle of deflection between numerical calculation and test

6 结论

提出头部刻槽形侵彻弹体设计，与同状态下的尖卵形弹体进行对比，通过LS-DYNA 数值模拟和侵彻10 层靶试验，分析侵彻过程中弹体姿态的变化规律。

（1）在0°攻角条件下，由于着角的原因弹体侵彻靶过程产生偏转力矩，导致弹体穿透单层靶后产生姿态偏转。

（2）在侵彻单层混凝土薄靶过程中，随初始攻角增大弹体姿态偏转角度增大，刻槽形弹体相对尖卵形弹体增大幅度趋缓，弹体姿态偏转相对较小。

（3）对比侵彻10 层混凝土靶试验结果，刻槽形弹体相对尖卵形可显著减少弹体偏转姿态，具有较好的侵彻弹道稳定性。