椭圆形截面聚能装药射流成型及侵彻特性

王钰婷，黄正祥，贾 鑫，马 彬，祖旭东，肖强强

（南京理工大学 机械工程学院，江苏 南京 210094）

1 引言

非圆截面外形已成为空中武器平台（巡飞弹、导弹等）重点考虑的外形布局形式［1-2］。目前非圆截面空中武器平台仍然采用传统旋转对称结构战斗部，使得弹身空间利用率低，战斗部毁伤威力受到限制，且增加了空间布局难度。因此，采用与武器平台外形特征匹配的战斗部结构势必将成为未来趋势。聚能战斗部可有效对付具有高效防护能力的装甲目标、工事，且不限制武器平台到达目标时存速，可成为非圆截面空中武器平台的战斗部。

目前，聚能战斗部的研究以轴对称聚能装药为主，仅少量学者开展了非圆截面聚能装药的研究。李砚东等［3-5］采用ANSYS/LS-DYNA 有限元软件研究了多点起爆下，半球形药型罩加装类圆矩形截面装药的聚能装药，发现形成的侵彻体为一种水滴状的高速成型弹丸，该研究是为了获得具有较大冲击起爆能力的侵彻体，因此，并未研究装药结构对侵彻体成型的影响。Cullis［6］采用三维欧拉数值计算程序研究中心点起爆下，金字塔形药型罩加装方形截面装药的聚能装药，发现形成的射流具有如下特征：靠近杵体的射流截面形状为星形，截面位置越靠近射流头部，其形状越趋近于圆形，该研究药型罩结构特殊，其应用前景受到限制。Stewart 等［7］设计的攻顶破甲兼侵彻功能的多模战斗部，射流运动方向明显偏离轴线，但该研究的射流成型受装药结构非轴对称与起爆点偏心的耦合作用，研究结 论 不 具 普 适 性。Wang［8］采 用ANSYS/LS-DYNA 有限元软件研究了旋转成体药型罩加装正方形截面聚能装药的射流成型及侵彻特性，发现形成的射流具有较高的侵彻能力，但该研究并未开展相关试验。可以看到，目前非圆截面聚能战斗部的研究尚处于初步探索阶段，现有的研究结论不能有效指导非圆截面聚能战斗部在非圆截面空中武器平台的应用。

椭圆形截面弹体是未来飞行器实现高升力、大升阻比飞行的潜在可行方案［1，9］，本研究提出一种适配于椭圆形截面弹体的椭圆形截面聚能装药：旋转成体药型罩加装椭圆形截面装药。通过开展椭圆形截面聚能装药的侵彻深度（DOP）试验，以及利用ANSYS/LS-DYNA 有限元软件构建椭圆形截面聚能装药的相关有限元模型，来分析椭圆形截面聚能装药的射流成型及对靶板的毁伤特性。研究结论对于椭圆形截面聚能装药在椭圆形截面空中武器平台的应用具有一定的参考价值。

2 试验

2.1 试验设置

椭圆形截面聚能装药结构如图1 所示，为旋转成体药型罩加装椭圆形截面装药。药型罩采用锥角为60°的单锥结构，直径为54.2 mm，高度为42 mm，厚度为1 mm。

选取装药截面短轴直径为56 mm，长短轴之比（long axis/short axis）分别为1、1.5、2的椭圆形截面聚能装药进行DOP 试验，装药高度均为73.3 mm，实物如图2所示。装药为铸装B炸药，药型罩材料为紫铜。为简化加工难度，铸药过程中采用尼龙壳体以保证装药特征尺寸；尼龙壳体厚度为3 mm，尼龙壳体作为低阻抗材料，对爆轰波的传播历程没有影响，可视作无壳聚能装药。

DOP 试验现场布置如图3 所示，包括雷管、扩爆药、扩爆药底座、聚能装药、炸高筒以及靶板；炸高为80 mm，炸高筒由硬纸板制成；靶板材料为45#钢。

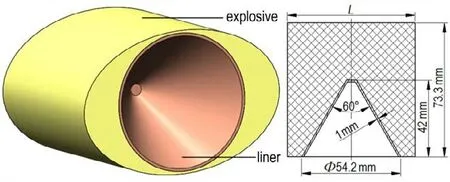
图1 椭圆形截面聚能装药结构示意图Fig.1 Structure of shaped charge with elliptical cross-section

图2 椭圆形截面聚能装药实物图Fig.2 Physical picture of shaped charges with elliptical cross-sections

2.2 试验结果及分析

图3 DOP 试验现场布置图Fig.3 Experimental setup of DOP tests

图4 DOP 试验靶板入孔图Fig.4 Entrance hole on target of DOP tests

试验后形成的靶板入孔如图4 所示，具体数据见表1。长短轴之比为1 的椭圆形截面聚能装药即为传统旋转对称结构聚能装药，因此，在靶板表面观察到一个直径为30 mm 的圆形侵彻孔。长短轴之比为1.5 和2 时，在靶板表面均观察到一个初始侵彻孔和两个偏移侵彻孔；偏移侵彻孔沿着装药截面短轴方向，关于装药截面长轴面对称分布，并与初始侵彻孔相接。长短轴之比为1.5时，初始侵彻孔平均直径为35.0 mm，偏移侵彻孔平均直径为26.5 mm，平均偏移距离为14.0 mm；长短轴之比为2时，初始侵彻孔平均直径为36.0 mm，偏移侵彻孔平均直径为24.3 mm，平均偏移距离为13.5 mm。长短轴之比从1.5 变化至2 时，平均偏移距离下降3.6%，可以认为射流的横向速度分布无明显差异。

试验后形成的靶板通道如图5 所示，具体数据见表2。长短轴之比为1 时，在靶板形成倒锥形单一侵彻通道，试验侵彻深度为150.0 mm。长短轴之比为1.5时，初始侵彻通道平均深度为47.5 mm，偏移侵彻通道平均深度34.0 mm；长短轴之比为2 时，初始侵彻通道平均深度为46.0 mm，偏移侵彻通道平均深度37.0 mm。可以看到，长短轴之比从1 变化至1.5 时，侵彻深度下降了68.3%；长短轴之比从1.5 变化至2时，初始侵彻通道深度下降3.2%，偏移侵彻通道深度增加8.8%，可以认为侵彻能力无明显变化。

表1 DOP 试验靶板入孔数据Table 1 Entrance hole data of target of DOP tests

图5 DOP 试验靶板通道图Fig.5 Penetration channel of target of DOP tests

3 数值模拟

3.1 模型建立

根据试验设置进行建模，为更好地研究截面长短轴之比对椭圆形截面聚能装药射流成型及侵彻特性的影响，数值模拟补充计算工况：截面短轴直径为56 mm，长短轴之比分别为1.2、1.4、1.6、1.8 的椭圆形截面聚能装药。

采用ANSYS/LS-DYNA 有限元软件，建立椭圆形截面聚能装药射流成型及靶板侵彻的三维有限元模型，如图6 所示。射流成型有限元模型由炸药、药型罩和空气3 部分组成，靶板侵彻有限元模型由炸药、药型罩、空气和靶板4 部分组成，炸高为80 mm。其中，炸药、药型罩和空气采用欧拉共节点网格，靶板采用拉格朗日网格。靶板与空气和药型罩间采用流固耦合算法；起爆方式为上表面中心点起爆。

3.2 材料模型及参数

炸药为B 炸药，采用高能炸药爆轰模型及JWL（Jones-Wilkins-Lee）状态方程描述［10］。

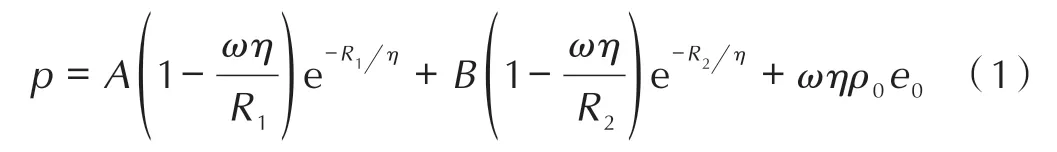
式中，η=ρ/ρ0；ρ 为材料平均密度，g·cm-3；ρ0为初始密度，g·cm-3；e 为 比 动 能，kJ·m-3；e0为 初 始 比 动 能，kJ·m-3；D 为爆轰速度，m·s-1；A、B、ω、R1及R2均为常数。B 炸药的主要参数见表3。

表2 DOP 试验侵彻深度数据Table 2 Penetration depth data of target of DOP tests

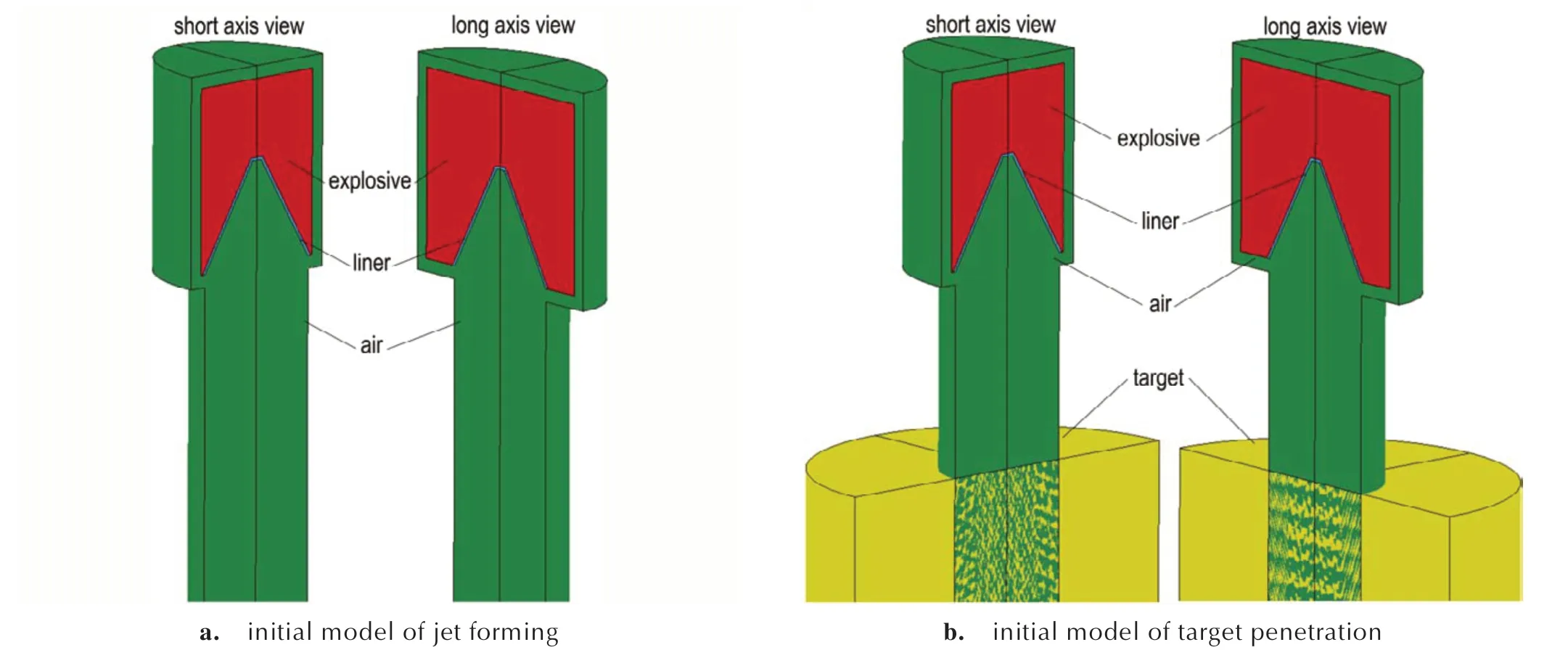
图6 有限元模型Fig.6 Finite element model

表3 B 炸药参数［11］Table 3 The parameters of Composition B

药型罩的材料为紫铜，靶板材料为45#钢，两种材料均采用Johnson-Cook 材料模型，状态方程采用Gruneisen 状态方程［10］。

式中，μ=ρ/ρ0-1；ρ 为材料变形后密度，g·cm-3；ρ0为材料初始密度，g·cm-3；C0为冲击波速度和粒子速度曲线的截距，km·s-1；S1、S2、S3为冲击波速度和粒子速度曲线的斜率系数；γ0为Gruneisen 常数；a 为对 应于γ0的常数。紫铜和45#钢材料的计算参数见表4。

表4 紫铜和45#钢材料的参数［12-13］Table 4 The parameters of copper and 45#steel

3.3 结果及讨论

3.3.1 药型罩压垮过程

选取典型试验结构为例，即长短轴之比为1.5 的椭圆形截面聚能装药，分析椭圆形截面聚能装药的药型罩压垮过程。中心点起爆后，爆轰波在装药中呈球形传播，在4 μs 时传播至药型罩顶部，如图7 所示。由图7 可知，爆轰波传播至短轴剖面的上表面边缘时，还未传播至长轴剖面的上表面边缘。然后，爆轰波陆续到达不同位置的药型罩微元表面，微元表面的炸药被引爆，药型罩微元在爆轰产物的初始压力作用下由静止向轴线压垮。随着药型罩微元向轴线压垮，形成一系列稀疏波［14］，微元表面爆轰产物的压力不断减小，药型罩微元做加速度减小的加速运动。

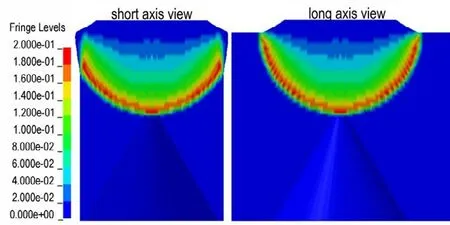
图7 4 μs 时，爆轰波传播至药型罩顶部Fig.7 The detonation wave propagates to liner top at 4 μs

6 μs 和14 μs 时，长短轴之比为1.5 的椭圆形截面聚能装药的药型罩表面压力云图如图8 所示。药型罩微元压垮运动初期，微元表面爆轰产物的压力不受从装药表面传入的稀疏波的影响，考虑到药型罩为轴对称结构，则6 μs 时，药型罩表面的压力分布呈轴对称性。药型罩微元压垮运动后期，微元表面爆轰产物的压力受到从装药表面传入的稀疏波的影响，考虑到装药为非轴对称结构，则14 μs 时，药型罩表面的压力分布呈非轴对称性。

6 μs 和14 μs 时，长短轴之比为1.5 的椭圆形截面聚能装药的药型罩微元速度云图如图9 所示。药型罩压垮运动初期，药型罩表面的压力呈轴对称分布，所以6 μs 时，压垮速度也呈轴对称分布。药型罩微元压垮运动后期，从装药表面传入的稀疏波陆续追赶上运动中的药型罩微元。考虑到从装药表面传入的稀疏波总是垂直于装药表面传入爆轰产物，因此，从装药表面传入的稀疏波总是最早影响截面短轴所在剖面的药型罩微元的压垮运动，最晚影响截面长轴所在剖面的药型罩微元的压垮运动。从装药表面传入的稀疏波到达药型罩微元表面后，在微元表面反射稀疏波，微元表面爆轰产物的压力的下降更为迅速，药型罩微元压垮运动的加速度的减小更为迅速，所以14 μs 时，截面短轴所在剖面的药型罩微元压垮速度最低，截面长轴所在剖面的药型罩微元压垮速度最高。

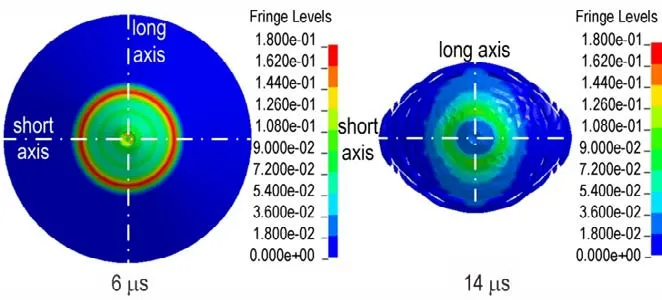
图8 6 μs 和14 μs 时，长短轴之比为1.5 的椭圆形截面聚能装药的药型罩表面压力云图Fig.8 At 6 μs and 14 μs，the pressure on liner surface of the shaped charge with elliptical cross-section，whose ratio of the long axis to short axis is 1.5

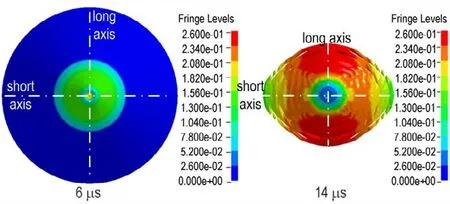
图9 6 μs 和14 μs 时，长短轴之比为1.5 的椭圆形截面聚能装药的药型罩速度云图Fig.9 At 6 μs and 14 μs，the collapse velocity of liner elements of the shaped charge with elliptical cross-section，whose ratio of the long axis to short axis is 1.5

众所周知，药型罩微元在向轴线压垮时，将受到相邻药型罩微元的作用，轴向上相邻药型罩微元具有不同的压垮速度，则会在药型罩母线方向上产生一个力的分量，使得药型罩微元沿着与表面法线呈一定角度的方向运动［15-16］。不同于旋转对称结构聚能装药，压垮运动受到从装药表面传入的稀疏波影响的椭圆形截面聚能装药的药型罩微元，周向上相邻药型罩微元具有不同的压垮速度，则也会在药型罩切线方向上会产生一个力的分量，使得在截面上，药型罩微元的最终压垮速度不是指向圆心，药型罩微元的压垮速度将存在沿药型罩切线方向的速度分量，如图10 所示。

3.3.2 椭圆形截面聚能装药的射流成型

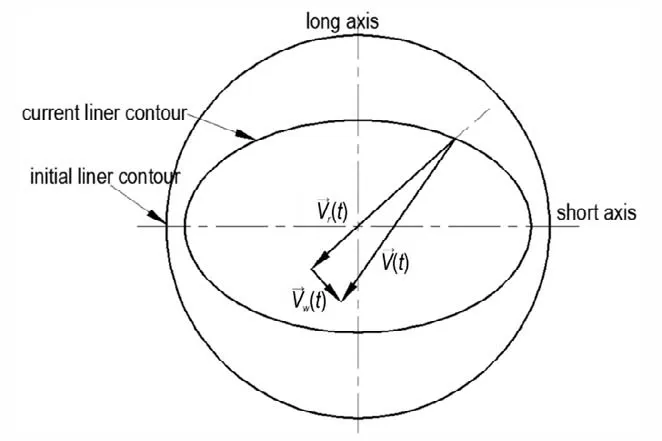
图10 截面上药型罩微元压垮速度的分量示意图Fig.10 The component diagram of collapse velocity of liner element in cross-section

同样以长短轴之比为1.5 的椭圆形截面聚能装药为例，分析椭圆形截面聚能装药的射流成型，其射流在不同典型时刻的形态如图11 所示。对于点起爆的椭圆形截面聚能装药，初始轴向位置相同的药型罩微元具有相同的质量流动率，则射流的剖面尺寸与相应药型罩微元的压垮速度呈反比［17］，形成射流头部的药型罩微元的最终压垮速度相同或者差异不明显，则射流头部截面形状尺寸差异很小；而形成其他位置射流的药型罩微元，截面长轴对应的最终压垮速度最高，截面短轴对应的最终压垮速度最低，则射流在装药截面长轴方向具有最小的尺寸，在装药截面短轴方向具有最大的尺寸；药型罩微元越靠近药型罩底部，最终压垮速度差异越大，因此，射流截面位置越靠近尾部，尺寸差异越明显。

图11 长短轴之比为1.5 的椭圆形截面聚能装药的射流在不同典型时刻的形态图Fig.11 At typical time，the morphology of the jet of the shaped charge with elliptical cross-section，whose ratio of the long axis to short axis is 1.5

长短轴之比为1.5 的椭圆形截面聚能装药形成的射流速度分布如图12 所示。由图12a 可知，射流具有轴向速度梯度，射流拉伸运动一段时间后，在距离射流头部21 mm 处，出现了明显的非凝聚现象，射流呈现关于截面长轴面对称分布的具有横向速度的两束流体，非凝聚的射流在轴向拉伸过程中很快发生颈缩断裂，形成一系列的断裂粒子。射流出现非凝聚现象的主要原因可能为压垮运动受到从装药表面传入的稀疏波影响的药型罩微元，其最终压垮速度存在沿药型罩切线方向的速度分量，以装药截面长轴所在对称面为界，左侧药型罩微元形成的射流具有沿截面短轴向左的横向速度，右侧药型罩微元形成的射流具有沿截面短轴向右的横向速度。初始位置越靠近底部的药型罩微元，其最终压垮速度在沿药型罩切线方向上的速度分量越大，且形成的射流越靠近尾部，则非凝聚的流体位置越靠近尾部，横向速度越大。

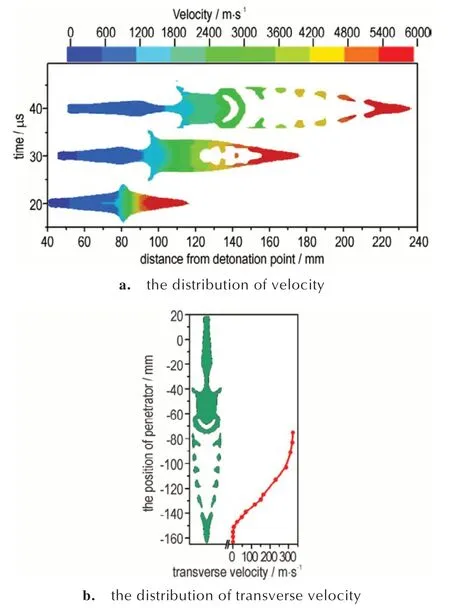
图12 长短轴之比为1.5 的椭圆形截面聚能装药的射流速度分布图Fig.12 The velocity distribution of the jet of the shaped charge with elliptical cross-section，whose ratio of the long axis to short axis is 1.5

3.3.3 椭圆形截面聚能装药的侵彻特性

炸高为80 mm 时，长短轴之比为1.5 的椭圆形截面聚能装药对靶板的侵彻过程如图13 所示。由图13可知，起爆后26 μs，射流头部运动到靶板表面，射流开始侵彻靶板，此时射流已经开始出现非凝聚现象；38 μs 时，射流的凝聚部分对靶板的侵彻结束；该炸高下，横向速度较小的非凝聚态射流到达靶板表面时，横向位移较小，射流依然可以继续增加侵彻深度；随着侵彻的进一步进行，横向速度较大的非凝聚态射流到达靶板表面时，径向位移大于初始侵彻孔孔径，则该部分射流将不再增加初始侵彻通道的侵彻深度，而是形成如图14 所示的偏移侵彻通道，偏移侵彻通道入孔沿着装药截面短轴方向，且关于装药截面长轴面对称分布，并与初始侵彻孔相接；72 μs 时，杵体到达侵彻孔底，对靶板的侵彻结束，最终侵彻深度为56.5 mm。

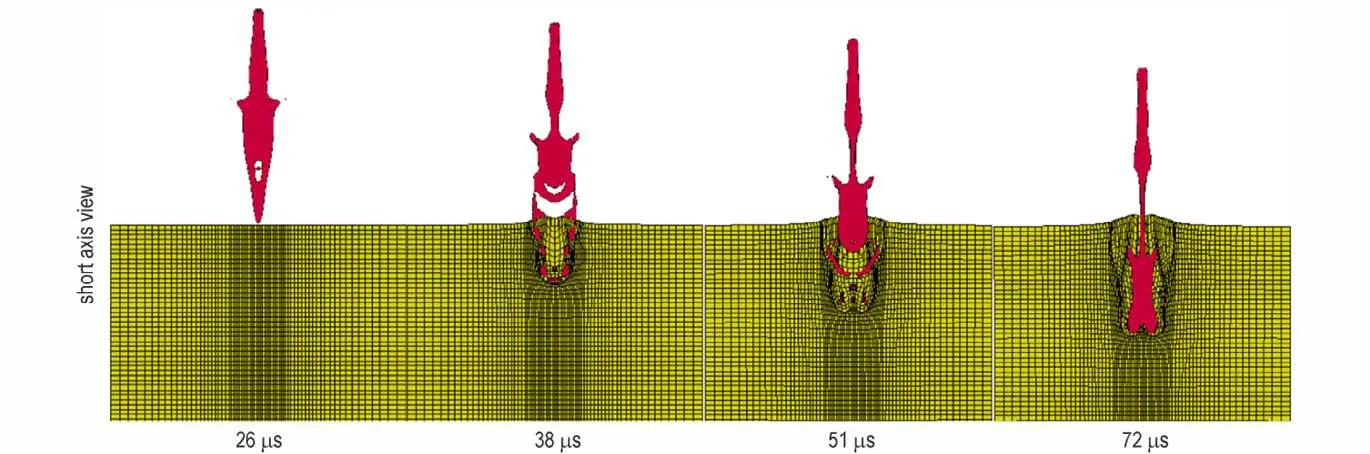
图13 炸高为80 mm 时，长短轴之比为1.5 的椭圆形截面聚能装药对45#钢靶的侵彻过程图Fig.13 Penetration process of the shaped charge with elliptical cross-section into 45# steel target at stand-off 80 mm，the ratio of the long axis to short axis of the cross-section is 1.5

图14 数值模拟的靶板入孔及侵彻通道Fig.14 Entrance hole and penetration channel of numerical simunation

3.3.4 长短轴之比对射流成型的影响

椭圆形截面聚能装药形成射流的横向速度与装药截面结构相关，因此，为研究截面长短轴之比对射流成型的影响，开展了截面短轴直径为56 mm，长短轴之比从1 到2 变化时，椭圆形截面聚能装药射流成型的数值模拟。

长短轴之比变化时，椭圆形截面聚能装药形成的射流在40 μs时刻的形态及横向速度分布模拟结果如图15所示。由图15可知，椭圆形截面聚能装药形成的射流拉伸运动后期普遍存在非凝聚现象。当长短轴之比小于1.6 时，长短轴之比越大，压垮运动受从装药表面传入的稀疏波影响的药型罩微元，其相邻微元的压垮速度差异越大，最终压垮速度在沿药型罩切线方向上的分量越大，则相同位置的射流的横向速度越大。装药半径大于一定值时，从装药表面传入的表面稀疏波将不再影响药型罩微元的压垮运动，装药长轴尺寸的增加并不会继续影响药型罩微元的最终压垮速度分布，则长短轴之比大于1.6后，射流横向速度分布不再发生明显变化。

图15 40 μs 时刻，各结构椭圆形截面聚能装药的射流形态及横向速度分布图Fig.15 The morphology and transverse velocity distribution of the jet of shaped charges with different elliptical cross-sections at 40 μs

3.3.5 长短轴之比对侵彻特性的影响

炸高为80 mm 时，椭圆形截面聚能装药对45#钢靶的侵彻深度与长短轴之比的关系如图16 所示。当长短轴之比小于1.4 时，随着长短轴之比的增加，相同位置的射流的横向速度显著增加，更多的射流不能到达初始侵彻通道底部，则侵彻深度随长短轴之比的增加而显著降低。当长短轴之比大于1.4 而小于1.6 时，虽然相同位置的射流的横向速度随长短轴之比的增加有轻微增加，但在该炸高下，这一轻微变化并未明显改变可以到达初始侵彻通道底部的射流占比；当长短轴之比大于1.6 时，射流的横向速度分布无明显变化，可以到达初始侵彻通道底部的射流占比无明显变化；因此，长短轴之比大于1.4 时，侵彻深度无明显变化。该炸高下，与长短轴之比为1 的聚能装药相比，椭圆形截面聚能装药的侵彻能力最高可下降61.4%。

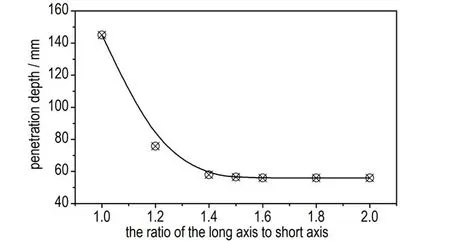
图16 炸高为80 mm 时，椭圆形截面聚能装药的侵彻深度随长短轴之比的变化情况Fig.16 When the ratio of the long axis and short axis changes，the penetration depth of shaped charges with elliptical cross-sections at stand-off 80 mm

图17 展示了长短轴之比分别为1、1.5 和2 时，椭圆形截面聚能装药侵彻45#钢靶的试验和数值模拟结果。可以看到，试验与数值模拟的入孔形状相似。长短轴之比为1 时，试验及数值模拟的侵彻通道形状相似，数值模拟得到侵彻深度为145 mm，与试验结果误差为-3.3%。长短轴之比为1.5 和2 时，试验与数值模拟的靶板通道形状呈现一定差异：试验初始侵彻通道深度小于数值模拟结果，试验的偏移侵彻通道深度大于数值模拟结果。长短轴之比为1.5 时，数值模拟得到初始侵彻通道侵彻深度为56.5 mm，与试验结果误差为18.9%；偏移侵彻通道深度为24.5 mm，与试验结果误差为-23.9%。长短轴之比为2 时，数值模拟得到初始侵彻通道侵彻深度为56 mm，与试验结果误差为21.7%；偏移侵彻通道深度为25 mm，与试验结果误差为-32.4%。

靶板侵彻通道深度的分配上数值模拟与试验出现较大的误差，分析原因可能为：数值模拟表征完全理想的情况，非轴对称聚能装药的加工难度较大，试验会偏离理想条件，使数值模拟与试验的射流横向速度分布存在一定的差异。

图17 试验和数值模拟结果Fig.17 Test and numerical simulation results

采用初始侵彻通道深度与偏移侵彻通道深度之和表征射流的侵彻能力。由图18 可知，长短轴之比为1时，侵彻深度误差为3.3%，长短轴之比分别为1.5 和2时，初始侵彻通道与偏移侵彻通道总体深度的数值模拟结果与试验结果误差分别为0.6%和2.4%。试验与数值模拟的靶板入孔形状相似，表明数值模拟可较好地反映椭圆形截面聚能装药的射流成型以及对靶板的侵彻特性。试验中，长短轴之比由1.5 变化至2 时，初始侵彻孔与偏移侵彻孔平均偏移距离无明显变化，表明射流的横向速度分布无明显变化，与数值模拟结果一致，表明数值模拟可较好的反映长短轴之比对椭圆形截面聚能装药的影响。

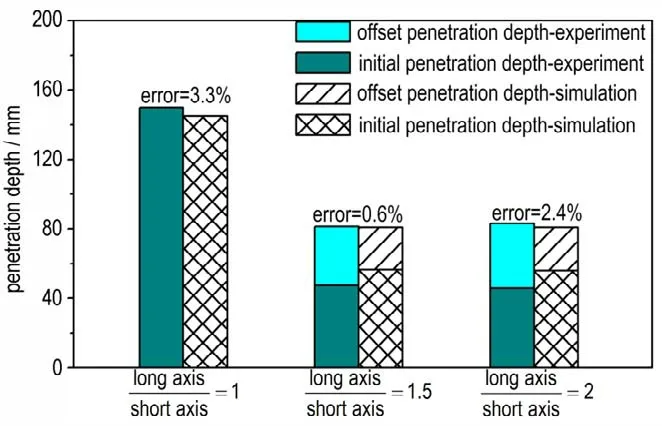
图18 试验与数值模拟结果对比图Fig.18 Comparison of test and simulation results

4 结论

开展了椭圆形截面聚能装药的DOP 试验，利用ANSYS/LS-DYNA 有限元软件构建相关椭圆形截面聚能装药的有限元模型，分析了椭圆形截面聚能装药的射流成型及对靶板的毁伤特性，研究了截面短轴一定时，长短轴之比对椭圆形截面聚能装药射流成型以及侵彻能力的影响。主要结论如下：

（1）椭圆形截面聚能装药的药型罩微元在向轴线压垮时，压垮运动受从装药表面传入的稀疏波影响的药型罩微元，其最终压垮速度将存在沿药型罩切线方向的速度分量，使得该部分药型罩微元碰撞形成的射流具有横向速度。因此，椭圆形截面聚能装药形成的射流，除射流头部在运动拉伸过程中持续呈凝聚态外，其余部分在运动拉伸后期呈非凝聚态，非凝聚的射流由关于截面长轴面对称分布的具有横向速度的两束流体组成。

（2）椭圆形截面聚能装药侵彻靶板时，横向速度较大的非凝聚射流不能到达初始侵彻通道底部增加侵彻深度，而是形成偏移侵彻通道，使得射流的侵彻能力大大降低。

（3）椭圆形截面聚能装药的截面短轴直径为56 mm，长短轴之比小于1.6 时，长短轴之比越大，相同位置射流的横向速度越大；长短轴之比大于1.6 时，射流的横向速度分布不再发生明显变化。

（4）椭圆形截面聚能装药的截面短轴直径为56 mm，长短轴之比小于1.4 时，在炸高为80 mm 下的侵彻深度随长短轴之比的增加急剧下降；当长短轴之比大于1.4 时，在炸高为80 mm 下的侵彻深度不再发生明显变化。