超高分子量聚乙烯纤维层合板抗侵彻性能的一种数值分析方法

曹铭津，陈 力，方 秦

（1. 陆军工程大学 爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007；2. 东南大学 爆炸安全防护教育部工程研究中心，江苏 南京 211189）

1 前言

纤维增强复合材料层合板（fiber reinforced polymer laminate，FRPL），具有高比强度和高比模量，耐腐蚀性强且抗疲劳性好等优点，广泛应用于航空航天，机械制造与军事防护等领域［1］。超高分子量聚乙烯纤维层合板（ultrahigh molecular weight polyethylene laminate，UHMWPEL）作为FRPL 的一种，通常由若干层UHMWPE纤维增强树脂基单层板薄膜经堆叠并热压加工而成，其与玻璃纤维层合板（GFRPL）、芳纶纤维层合板（AFRPL）以及碳纤维层合板（CFRPL）相比具备更高的比强度、比模量［2］和更优异的抗冲击侵彻性能［3-4］，一直是防护工程领域研究的热点。目前用于分析FRPL 抗侵彻性能的主要方法有试验测试法［5-6］、解析模型分析法［7］和数值分析法［8］。随着商用有限元软件的不断进步，数值计算逐渐成为一种适用于FRPL 损伤失效分析的有效且经济的手段。推动FRPL 的数值计算的发展，对于提高科研人员研究效率，降低研究成本，具有重要的意义。

Menna 等［9］通 过LS-DYNA 软 件 分 析 了两种厚度GFRPL 在低速冲击荷载作用下的力-位移曲线，发现层间损伤是GFRPL 的一种主要失效模式。鲍盘盘［10］基于ABAQUS 进行子程序二次开发，计算了不同厚度GFRPL 的弹道极限速度v50，结果误差均小于10%，但其采用的损伤演化准则为试算法，缺少具体的物理机制支撑。古兴瑾等［11-12］基于粘弹性用户子程序模型对Kevlar/epoxy 层合板抗侵彻性能开展了研究，得出了侵彻过程中弹体直径与剩余速度、能量吸收之间的关系；发现提高纤维的强度可以显著提高层合板的抗侵彻性能，而提高基体强度则有利于降低损伤面积；粘弹性模型方法准确性相对较高，但是材料参数多而复杂，标定难度大。López-Puente 等［13］基于ABAQUS/Explicit 研究了圆球弹侵彻速度与层合板损伤面积的关系，给出了弹体侵彻贯穿碳纤维层合薄板的过程中初始速度与残余速度之间的关系。秦建兵等［8］研究了不同弹头形状对层合板抗侵彻性能的影响规律，指出平头弹破坏最严重，球头弹居中，而锥头弹破坏程度最低，其模型中采用了壳单元，忽略了厚度方向的应力且未考虑分 层影响。Lassig 等［14］基于AUTODYN 研究了UHMWPEL 在直径6 mm 的铝球超高速冲击作用下的破坏状态和残余速度，但是对分层破坏机理未作详细 探 讨。Nguyen 等［15］采 用AUTODYN 对 弹 体 在300～1000 m•s-1冲击速度范围内UHMWPEL 的损伤状态进行了数值研究，但其所采用的分层模型未考虑损伤演化且未考虑法向压应力对分层的抑制作用。已有的研究成果表明，对弹丸冲击侵彻层合板的数值模拟是一个较为复杂的过程，已有的数值计算模型各有其自身的局限性，例如材料损伤演化模拟缺少物理支撑［10］，材料参数难以获取［11-12］，二维壳模型难以模拟分层破坏现象［8］以及对层合板分层破坏描述过于简化［14-15］等问题。

针对已有研究成果的不足，本研究采用三维准宏观分析尺度建模，将层合板离散为若干单层板以及cohesive 黏结层两部分，同时考虑UHMWPEL 基于断裂韧性的渐进损伤演化物理机制，发展了一种用于分析UHMWPEL 弹道性能的精细化数值建模方法。

2 材料模型VUMAT 开发

2.1 单层材料损伤起始和演化

（1）损伤起始准则

层合板损伤破坏可分为单层板损伤破坏和界面层损伤破坏两个部分。针对FRP 单层板的损伤起始准则，国内外学者已做了大量的研究［18-19］。本研究选取工程上应用较广、精度可靠的3D Hashin 准则［20］来描述UHMWPE 单层板材料，该准则将单层板的损伤失效分为：纤维拉断、纤维压断、基体拉裂和基体压裂四种形式，当fi≥1 时，损伤开始发生：

纤维拉坏(σ1≥0)

纤维压坏(σ1＜0)

基体拉坏(σ2+ σ3≥0)

纤维压坏(σ2+ σ3＜0)

式中，fi的下标i 代表了单层板对应的损伤失效模式，当i=1，2，3，4 时分别对应纤维拉坏、纤维压坏、基体拉坏和基体压坏。

（2）损伤演化准则

Chen 等［21］对单向UHMWPEL 进行了动态拉伸试验，发现其应力—应变关系曲线具有如图1 所示的典型双线性特征。因此，单层板选取双线性模型。在材料未损伤之前，材料应力随应变呈线性变化，当材料到达损伤起始点后，随着荷载继续增加，单层板内部产生裂纹和孔隙等微观缺陷，导致刚度退化，应力随应变呈线性下降。材料在变形过程中，应力应变曲线与坐标系围成的面积即为材料渐进破坏过程中所耗散的断裂能，当满足损伤起始准则的单元在渐进破坏的过程中消耗的能量达到断裂能的临界值时，认为材料发生破坏。Balzani［22］已 研 究 证 明 双 线 性 模 型针 对FRPL 类 材料完全能够兼顾求解效率和精度。

图1 单层板损伤本构关系Fig.1 Constitutive equation of single lamina

基于连续介质损伤力学，定义损伤变量为di（i=1，2，3，4），

由于裂纹扩展单位面积所需断裂能的大小是材料的固有属性，因此采用断裂能的方法计算单元的失效应变，同时为了降低网格相关性，引入单元特征长度［24］：

式中，l 为单元特征长度，mm；ABAQUS 软件默认其值大小为单元体积的立方根；Gic为单层板临界断裂能，

由于纤维在单层板某一方向的增强，使单层板具有典型的正交各向异性关系，损伤后的应力-应变关系可表示为［20］：

式中，Cij和Gij分别为损伤后的刚度张量，MPa，i = j = 1时，Cij中的dm为0；上标0 代表无损状态；υij为泊松比张量；δij为克罗内克符号；df和dm分别为纤维和基体总损伤变量；smt和smc分别为损伤控制系数，参考Lee［26］取smt= 0.9，smc= 0.5。

2.2 Cohesive-Zone 界面层损伤起始和演化

UHMWPEL 由单层板材热压而成［5］，由于厚度方向缺少增强机制，分层是层合板在冲击荷载下的主要破坏模式之一。在冲击荷载作用下，由于压缩波在层合板背部自由面反射为拉伸波，由此产生的拉应力会加剧层合板的分层破坏，因此通常的二维模型已不能满足要求，需要采用三维模型来提高分析精度。本研究采用共节点cohesive-zone 界面单元来模拟分层现象，采用二次应力准则［27］作为界面单元损伤起始准则；采用B-K 准则［28］计算界面层损伤扩展。为了方便改进材料模型，同样将含损伤演化的cohesive 本构编入用户子程序VUMAT。

Cohesive-zone 方法基于断裂力学和损伤力学，最早 由Dugdale［29］和Barenblatt 等［30］提出，该法既可以预测裂纹的发生，又可以预测裂纹扩展，具有显著的优越性［27］，但对网格尺寸有一定要求［31］。黏结层通过具有一定厚度的黏结单元实现，其与上下单层板单元之间通过共节点连接，黏结单元本构关系为，

式中，σn，σs和σt分别为界面层法向应力和两个面内剪应力，MPa；εn，γs和γt分别为法向应变和两个剪切应变，Enn，Ess和Ett为刚度参数，MPa。

Quads［27］损伤起始准则为：

当界面单元受力状态满足损伤起始准则后，随着荷载的继续增加纤维材料将发生损伤，Balzani［22］已证明线性损伤模型对于FRPL 具有较高准确性，因此这里同样采用线性损伤模型，定义损伤变量D 为：

式中，ε0，εf和ε 分别为损伤起始等效应变，损伤失效等效应变和在损伤累积中达到的最大真实等效应变且应满足ε ＞ε0，εf采用B-K 准则［28］基于断裂能求得，具体可参考文献［32］。

损伤后的界面单元本构关系为：

当D = 1时，界面单元破坏删除，单层板发生分层。

3 UHMWPEL 有限元模型的建立

3.1 试验介绍

UHMWPEL抗FSP侵彻的试验案例来自于Nguyen等［5，15］开展的相关试验。试验标准依据MIL-STD-662F［33］进行，UHMWPEL 靶板呈［0/90］ns正交铺设，尺寸为300mm×300mm×10mm和300mm×300mm×20mm，密度为0.98 g•cm-3，靶板厚度方向平行于地面放置且上下两端通过钢板夹持，背面悬空无支撑［5］，示意图如图2a 所示；楔形圆柱体FSP［34］直径20 mm，长24 mm，洛氏硬度为30，密度7.88 g•cm-3，通过调整发射装置实现FSP 以不同速度垂直正冲击靶板［5］，采用弹体测速装置获取FSP 初始速度以及残余速度，采用高速摄像机观测靶板变形破坏状态。试验操作其他细节及试验中UHMWPEL 变形破坏过程详见文献［5］，弹体初始速度以及残余速将在4.1 节给出，详见文献［15］。

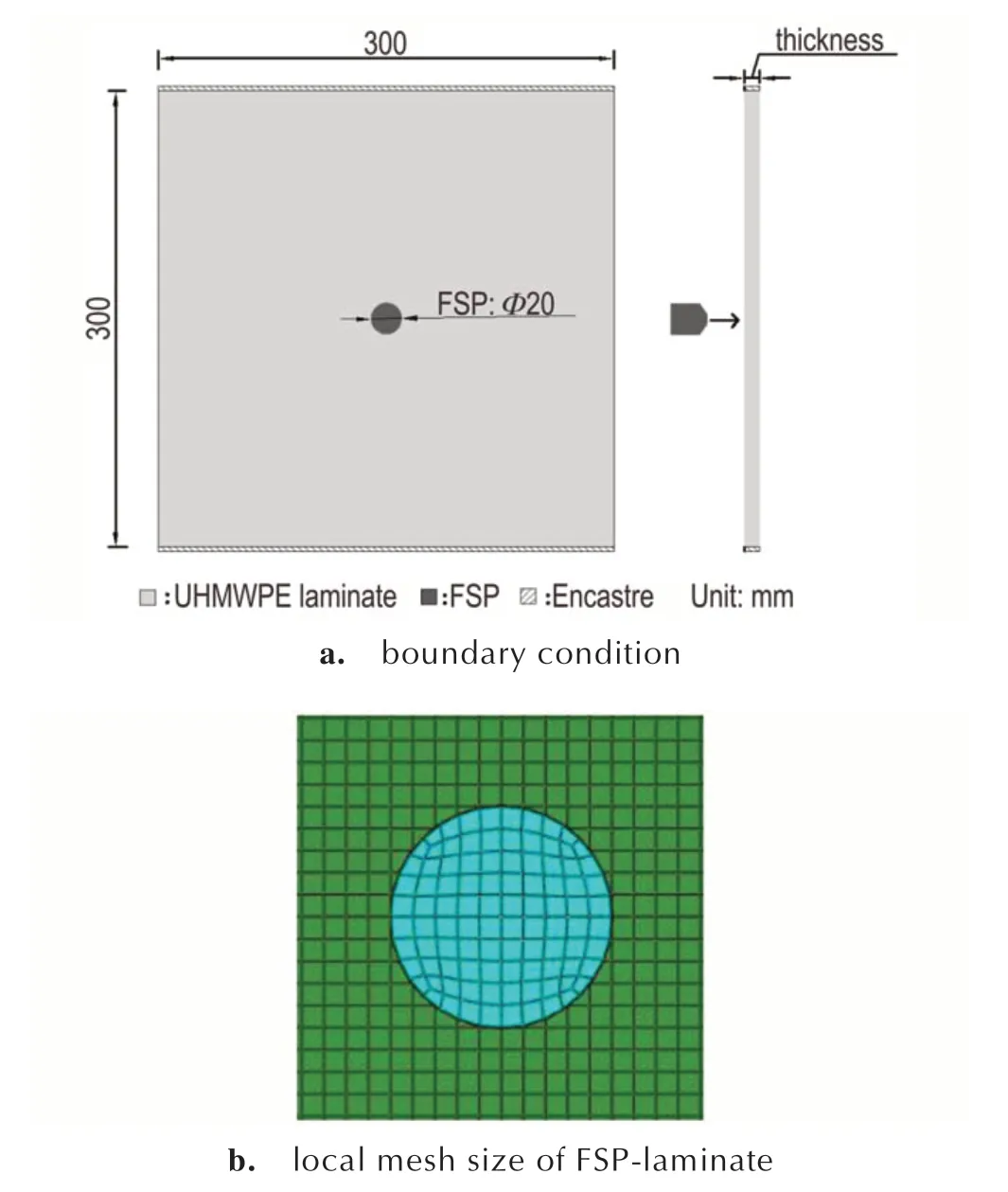
图2 边界条件及网格大小示意图Fig.2 Diagrams of boundary condition and element size

3.2 有限元模型

有限元模型单元划分方法：单层板采用线性缩减积分六面体单元C3D8R，单元尺寸为2 mm×2 mm×2 mm，沿厚度方向划分为5 层，勾选组合沙漏控制［35］以及单元删除；每两层单层板之间通过单元共节点加入一层cohesive 单 元（COH3D8），如 图3a 和 图3b 所 示；cohesive 单元作为一种黏性单元，受面内法向拉、压及面内两个方向的剪切作用，如图3c 所示；cohesive 单元的几何厚度为0.01 mm，物理厚度为1 mm，其中几何厚度仅用于模型显示，物理厚度参与模型计算；cohesive 单元面内尺寸与单层板相同，勾选单元删除。由于弹体变形很小，因此采用离散刚体，网格尺寸2 mm。有限元模型边界条件：层合板上下两端限制位移；对子弹施加沿板厚方向的初始速度，约束其他方向的位移及转动。接触类型为通用接触。有限元模型边界条件及网格大小如图2 所示。单层板以及界面层的材料参数［14-15，36］见表1、表2。其中表1 为单层板的材料参数，单层板的临界断裂能根据文献［15］中单元本构曲线近似反推得到，为了使分层破坏通过界面cohesive 单元实现，单层板厚度方向的拉压强度取一近似无穷大值；界面层密度近似取1.0 g•cm-3，表2 为界面层材料参数，界面层单元的临界断裂能参考文献［37］确定。

图3 黏结层示意图Fig.3 Sketch map of cohesive

表1 UHMWPE 单层板材料性能参数Table 1 Material properties of single layer lamina

表2 cohesive 界面单元性能参数Table 2 Material properties of cohesive interface layer

4 FSP 侵彻计算结果验证和讨论

4.1 侵彻破坏过程模拟

采用2.1 节、2.2 节 所述的UHMWPEL 本 构 以及3.2 的有限元模型计算文献［5］试验中UHMWPEL 抗侵彻破坏过程，结果如图4 所示。

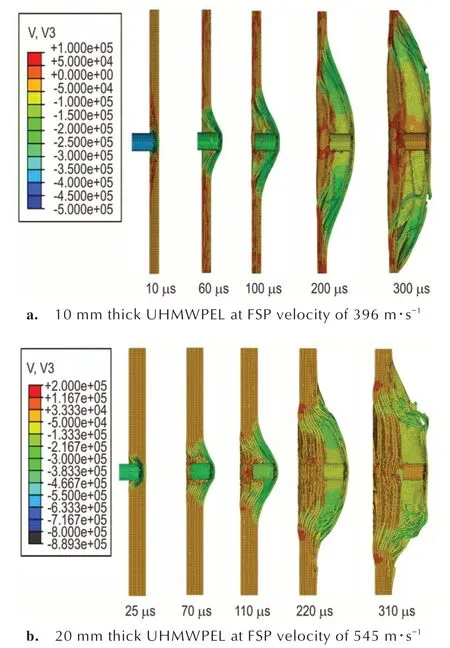
图4 弹速接近弹道极限速度时UHMWPEL 抗侵彻破坏过程Fig.4 Penetration failure process of UHMWPEL when FSP velocity approaches v50

由图4a 可知，当FSP 冲击速度接近层合板弹道极限速度v50（396 m•s-1）时，FSP 冲击厚层合靶板的破坏过程主要分为两个阶段：第一阶段如图4a 中10 μs 和60 μs 所示，弹体冲切进入靶板，如10 μs 时弹靶已经发生冲切接触，但此时靶板背面无明显鼓包，随着弹体冲切进入靶板一定深度后，继而背部产生较小的鼓包，冲切破坏后的单层板基本丧失承载能力；为了验证并直观观察这一破坏模式，截取弹靶接触位置处单层板片层破坏有限元计算图，如图5a 中黑色箭头所指示位置，层合板沿FSP 锋利边缘处发生了明显的冲剪破坏。

冲切过程中弹体速度快速降低（如图6a 中曲线S1阶段），冲击荷载主要由靶体局部承受，分层破坏现象主要集中在冲击部位，局部破坏效应非常明显。第二阶段如图4a 中100～300 μs 所示，靶板冲切破坏后已经吸收掉部分弹体动能，此后弹体速度降低并且降速逐渐减缓，如图6a 中曲线S2 阶段，靶体破坏模式由冲切破坏转为纤维拉伸破坏以及黏结界面处分层扩展，靶体背部产生较大鼓包；由100 μs 时的破坏形态发现，此时弹体前方的单层板内纤维的应力状态未达到其破坏应力，能量耗散主要通过各单层板的变形以及界面层的失效破坏实现；随着弹体动能继续耗散，界面层的损伤逐步扩展，直到不再具有承载能力，层合板发生严重的分层破坏，如200 μs 的计算结果所示；此时弹体的剩余动能由单层板继续吸收，由于约束了层合板上下边界的位移，限制了单层板的完全剥离，最终通过单层板中纤维拉伸断裂完成了对FSP 能量的消耗，成功拦截了弹体。文献［5］显示，当UHMWPEL 靶板厚度小于10 mm 时，由于侵彻贯穿过程十分短暂，难以成功捕捉到破坏全过程画面，而通过本研究提出的数值模拟方法，则可以再现其出攻击破坏过程，揭示其侵彻破坏机理，数值模拟的层合板变形破坏过程与试验观测基本一致。

同样，当FSP 以接近20 mm 厚UHMWPEL 弹道极限速度的初始速度（545 m•s-1）冲击20 mm 厚UHMWPEL 时，层合板同样表现出与10 mm 层合板类似的两阶段侵彻破坏特性：首先是冲塞剪切破坏和局部鼓包，如图4b 中25，70 μs 及图6b 中S1 阶段所示；第二阶段为分层扩展及大范围鼓包阶段，纤维受到明显的拉伸作用，如图4b中110～310 μs及图6b中S2阶段所示。

图5 UHMWPEL 冲切破坏Fig.5 Shear failure of UHMWPEL

图6 给出了不同冲击速度FSP 侵彻UHMWPEL 靶板的速度变化过程。可以发现，当FSP 以396 m•s-1和397 m•s-1侵彻10 mm 层合板时，弹体速度变化曲线经历了较长的下降段（S1+S2），应力波（尤其是横波）在靶板面内方向得以广泛传播，UHMWPEL 发生显著的凸起变形、分层，纤维出现大量拉伸断裂破坏（如图4a），吸收了几乎全部的弹体动能，充分发挥了层合板的抗冲击性能。而当FSP 以470～985 m•s-1侵彻10 mm 层合板时，冲击过程速度变化曲线下降段近似线性且很短（小于100 μs），UHMWPEL 被迅速贯穿。例如985 m•s-1时靶板穿透时程约15 μs，靶板穿透破坏如图7a 所示，靶板鼓包变形很小，分层仅集中在穿孔小范围附近。在470～985 m•s-1初始弹体范围内，FSP 侵彻过程速度变化曲线线形高度相似（图6a），表明其速度衰减规律相同，层合板侵彻破坏的机理相近，故而仅给出985 m•s-1时UHMWPEL 破坏示意图。同理，类似的现象也出现在20 mm 厚UHMWPEL 中，如图6b 和图7b。当弹速接近层合板弹道极限速度时冲击UHMWPEL，弹速变化曲线经历了较长的下降段，UHMWPEL 发挥了其大变形耗能特性，而当弹速明显高于层合板弹道极限速度时，弹速变化曲线下降段近似线性且很短，UHMWPEL 被迅速穿透，破坏模式单一，材料的性能未被充分发挥。可见，当弹体冲击速度大幅超过UHMWPEL 弹道极限速度时，UHMWPEL 局部破坏严重，纤维的强拉伸耗能以及层间大面积分层的优势未得到充分发挥，因此在抗高速侵彻时可设计多材料复合型靶板并将UHMWPEL 设置在复合靶板的中部或背部，由前部的靶板将弹体镦粗或将弹速降至UHMWPEL 弹道极限速度附近，以充分发挥UHMWPEL 的分层破坏及凸起变形吸能特性。

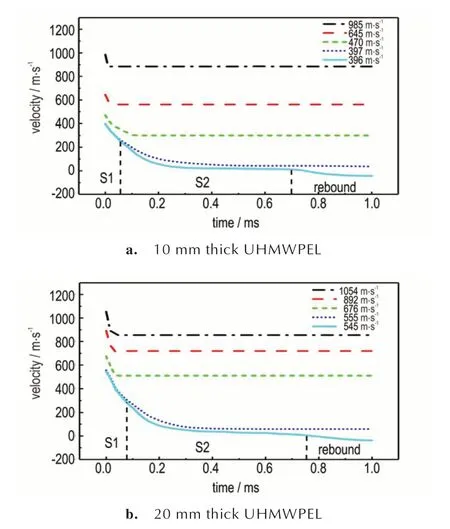
图6 弹体冲击UHMWPEL 速度变化过程Fig.6 Velocity changes of FSPs during impacting UHMWPEL

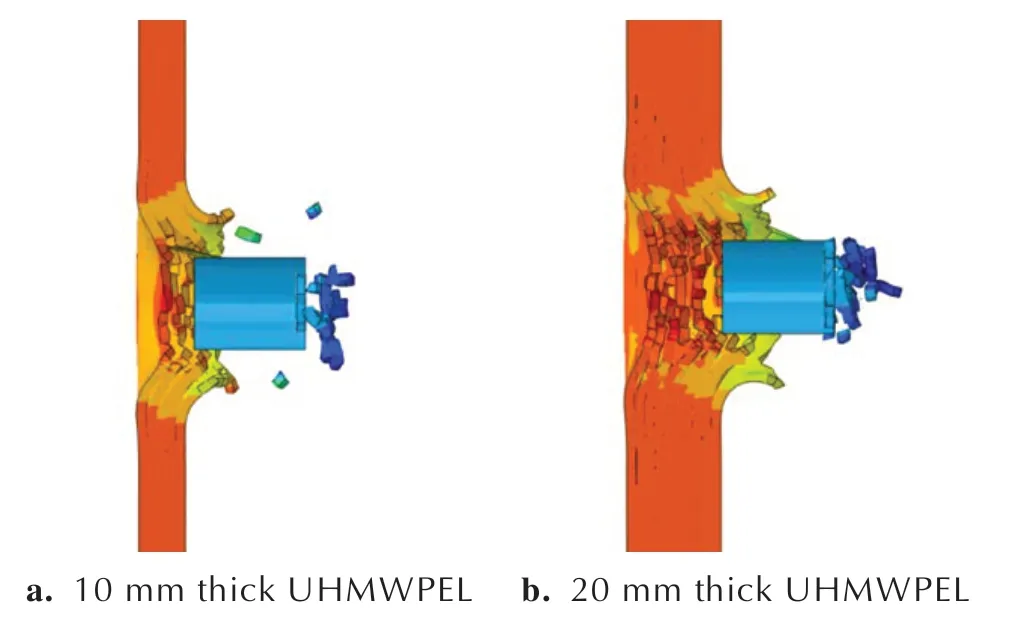
图7 UHMWPEL 高速侵彻局部效应计算图Fig.7 Local effects of high speed penetration of UHMWPEL

4.2 弹体残余速度预测

采用2.1 节、2.2 节 所述的UHMWPEL 本 构 以及3.2 节的有限元模型计算出的文献［15］试验中20 mm口径FSP 侵彻10，20 mm 厚UHMWPEL 后的弹体残余速度见表3 和表4。

表3 10 mm 厚UHMWPEL 残余速度预测Table 3 Prediction of residual velocities of 10 mm thick UHMWPEL

表4 20 mm 厚UHMWPEL 残余速度预测Table 4 Prediction of residual velocities of 20 mm thick UHMWPEL

UHMWPEL 弹道极限速度v50的计算参考GB/T32497-2016［38］，规范中要求：两发弹体有效命中时，若两发子弹速度差不大于15 m•s-1且存在一发穿透和一发阻断，则取这两发的测点弹速的算术平均值作为层合板的弹道极限速度v50。10 mm 厚UHMWPEL弹道极限速度v50的试验值为394 m•s-1，数值计算结果为396.5 m•s-1，误差约0.6%，20 mm 厚UHMWPEL弹道极限速度v50的试验值为620 m•s-1，数值计算值为550.0 m•s-1，计算结果偏保守，误差约11.3%。可见，本研究所采用的本构模型以及有限元模型对UHMWPEL 弹道极限速度的预测精度具有一定可靠性，对UHMWPEL材料防弹抗冲击的防护设计具有参考价值。表3 和表4 中FSP 残余速度vr数值模拟结果的负值，表示弹体被靶板拦截后发生反向弹射，如图6 中的rebound 阶段。vr试验值的符号“-”表示缺少试验值，此处目的仅是通过数值模拟手段计算出层合靶体弹道极限速度，因此不需要真实的vr试验值。如表3 和表4 所示，采用本研究方法计算的两种厚度UHMWPEL 在FSP 以不同初始速度侵彻贯穿后的残余速度预测误差最大不超过15%，与试验值吻合较好，进一步验证了提出的数值模拟方法的可靠性。

5 结论

基于ABAQUS 平台进行用户动态材料子程序VUMAT 的二次开发，考虑了分层破坏特性，发展了一种适用于三维复合材料层合板冲击侵彻计算的数值分析方法，建立了基于断裂能的UHMWPEL 抗侵彻有限元计算模型，模拟计算了FSP 冲击靶板的损伤破坏过程并预测了弹体的残余速度，计算结果得到了试验验证，主要结论为：

（1）采用正交各向异性的单层板本构、Cohesive-Zone 黏性界面层以及基于断裂韧性损伤演化的组合模型方法，能够准确预测UHMWPEL 的变形破坏过程及抗侵彻性能。

（2）提出的数值分析模型对10 mm 厚UHMWPEL弹道极限速度预测误差约为0.6%，对20 mm 厚UHMWPEL 弹道极限速度预测误差约为11.3%。对弹体残余速度预测值的最大误差不超过14.2%。

（3）模拟结果揭示了UHMWPEL 的抗侵彻作用机理，与已有试验吻合。当弹体速度小于或接近UHMWPEL 弹道极限速度时，靶板的冲击破坏过程具有典型的两阶段特性，第一阶段为层合板冲切破坏及局部鼓包，第二阶段为大范围鼓包、整体性分层以及纤维拉伸破坏。当弹体速度明显大于UHMWPEL 弹道极限速度时，靶板的冲击破坏特性为单一的通透性冲切穿孔，并在开孔周边很小范围内形成局部分层。

（4）鼓包变形（纤维拉伸）以及分层破坏是UHMWPEL 消耗弹体动能的重要方式，因此UHMWPEL 适合抵抗接近或小于其弹道极限速度的弹体冲击。当弹体速度显著超过UHMWPE 弹道极限速度时，设计多材料复合型靶板并主要将UHMWPEL 作为背衬材料来抵抗弹体的高速、超高速冲击是UHMWPEL 重要的推广应用方向。