螺栓预紧过程的有限元仿真研究

桂学文 张京东 廖日东

螺栓预紧过程的有限元仿真研究

桂学文 张京东 廖日东

(北京理工大学 机械与车辆学院，北京 100081)

预紧过程直接关系到螺栓结构的强度计算和松动分析，但是螺栓的预紧过程是一个复杂的非线性问题，目前对于预紧后螺栓的受力状态、接触状态以及不同加载方法的差异等方面的认识尚不完善。本文建立了精细的螺栓六面体网格模型，对转角法和预紧单元法两种不同加载方法进行了仿真研究。基于转角法研究了扭矩、转角、预紧力之间的关系，为一些特殊螺纹连接的扭拉关系研究奠定了基础。并对比分析了两种加载方法下螺栓预紧后的受力和接触状态。结果表明，本文采用的转角法加载能够准确的模拟螺栓的拧紧过程，预紧单元法只能模拟轴向力的分布，并不能准确考虑切向力的影响。

螺栓连接；预紧过程；扭拉关系

0 引言

螺栓是一种与螺母配合使用的螺纹紧固件，工程中螺栓预紧一般是对螺母施加扭矩，使之相对螺杆转动一定角度，利用螺母和螺杆上内外螺纹的相互作用使螺母和螺杆之间发生相对轴向运动，夹紧被连接件从而实现紧固作用，这就是所谓的转角法。在一些特殊情况下，如超大规格螺栓的应用时，由于所需扭矩太大不方便施加，也会采用先拉伸螺杆到一定长度后，再将螺母用很小的扭矩拧紧到位的预紧方法（简称拉伸法）。

螺栓预紧过程研究一方面是要探明给定结构条件下，达到给定预紧力所需螺母的转动角度（扭矩）或者螺栓的拉伸长度，以指导安装工艺设计；另一方面是获得预紧时螺栓和螺母的应力状态和接触状态，以支撑强度计算和松动分析。

但是，由于试验测试的困难，人们对螺栓预紧状态的认识以及有关因素的影响规律并不深刻。因此，开展螺栓预紧过程的仿真研究，对加深螺栓预紧状态的认识，实现螺栓结构的预测设计具有重要的理论意义和工程价值[1]。

已有针对螺栓预紧过程的研究主要分为对预紧力的控制和对载荷分布的研究。机械设计教材一般都给出了螺栓结构的扭拉关系式，指出螺栓的拧紧扭矩与预紧力近似满足线性关系[2]。这个关系式是目前螺纹紧固件结构设计和装配设计中最重要的依据。但是，这个关系式一般只适用于常规的三角形螺纹、矩形螺纹，对如今一些广泛使用的新型紧固件，如自锁螺母，其收口设计会使螺纹变形，产生额外的初始自锁扭矩[3]，该关系式就不再适用。

研究有关因素对螺纹连接结构扭拉关系的影响，实现对装配过程更准确的控制一直是研究人员努力的方向，如大连理工大学的陈德安[4]研究了几何偏差对预紧力和拧紧扭矩的影响，侯博文[5]考虑了接触表面形貌对拧紧工艺进行研究，得到不同参数下不同拧紧工艺的误差范围，徐卫秀等人[6]研究了摩擦因数、结构材料对扭矩系数等的影响，为实际装配的拧紧工艺提供了理论参考。

对于螺纹结构载荷分布的研究，最重要的工作当属英国国家物理实验室的Sopwith[7]和东京工业大学的山本晃(Yamamoto)[8]给出的螺纹副表面轴向载荷分布的解析结果。这个结果对螺栓受拉螺母受压的螺纹结构强度设计具有重要的启示意义。但由于该结果是基于线弹性假设的，因此难以应用在大载荷螺纹结构的设计计算上，另外这个结果也没有涉及螺纹结构所受的横向载荷。曾攀等人[9]通过光弹实验，测得螺母的轴向载荷分布，与解析解吻合，但由于光弹实验材料的限制，只能适用于很小载荷的情况。

而实际也存在一些螺母承受拉力的情况，如使用螺纹张紧器时，大连理工大学的李志彬[10]采用离散化方法得到螺栓螺母同时受拉时的载荷分布解。华北电力大学的江文强等人[11]则给出受横向载荷时螺纹副上的横向力分布，并以此计算出螺栓连接的临界松动载荷，但缺乏实验或仿真的验证，且实际上轴向载荷也会造成螺纹副上的横向力的不均匀分布，这也会影响临界松动载荷的计算。有限元仿真可以获得螺纹连接接触面的实时力学行为和相对运动状态，更有效的进行螺纹连接问题的研究。但螺栓连接结构建模复杂，时间成本高。根据研究的侧重点的不同，通常对模型进行不同程度的简化，对一些关注重点是整体连接结构的计算问题，建模时可以忽略螺纹部分，或者将螺栓简化成梁单元、刚性单元连接等模型[12]。若进行螺栓的强度校核，分析螺纹牙上的承载力分布和变形情况，可以忽略螺旋升角，建立简化轴对称模型，将三维问题转化为二维问题[13]。但扭拉关系、松动等问题研究需要考虑螺旋升角产生的扭矩[14]，必须建立考虑升程的三维螺纹连接有限元模型。

但要建立精度和效率俱佳的三维螺纹连接有限元网格模型存在很大的困难。四面体网格划分的网格质量差，将螺纹部分独立建模再绑定于螺杆上的方法的计算结果不准确[14]。2008年日本学者Fukuko[15]提出一种一体化六面体网格划分方法。该方法利用了螺纹各横截面的轮廓曲线的一致性，基于轮廓线方程建立二维网格模型，再旋转平移得到不同高度的网格模型，构造出完整的六面体网格的螺纹有限元模型。目前学者建立的精确的螺纹连接模型多采取此种网格划分方法。

有限元仿真中预紧力加载可通过多种方式实现，如温度载荷法、过盈配合法[16]。这两种方法需要试算迭代，使用较少，目前多采用的加载方法为预紧单元法。这些方法可以看作是实际中拉伸法的仿真模拟。而对实际的拧紧过程的仿真则需要使用旋转螺母的转角法。但由于计算效率、仿真结果的收敛性等原因，转角法仿真的实现并不简单，如文献[17]基于动力学求解器实现转角法加载，得到预紧力、扭矩、转角关系并非线性，预紧力以及转角增加过程有“台阶”现象，这一仿真结果并不准确。目前的研究中经常采用预紧单元法代替拧紧过程的预紧力加载，如文献[18]、[19]分别用不同的预紧力加载方法研究了横向振动条件下的松动过程，没有考虑两种加载方法的差别，只是为了达到产生夹紧力的效果。

因此本文利用有限元分析软件ABAQUS，采用两种预紧力加载方法对螺栓的预紧受力过程进行了仿真分析，讨论了不同的预紧力施加方法对结果的影响，对比分析加载后的受力、接触状态的差异，为今后仿真计算应采取何种预紧力加载方式提供参考。并基于转角法加载研究了扭矩、转角、预紧力之间的关系，得到了沿螺栓螺纹面的接触应力分布，螺纹副的轴向以及横向载荷的分布规律。

1 螺栓连接结构有限元建模

本文研究的是普通的三角形螺纹连接结构，其示意图如图1所示，主要的尺寸参数见表1。该系统由螺栓、螺母和两块被夹紧件组成。其中螺栓规格为M8，内外螺纹间隙0.1mm，所有材料均为合金钢，弹性模量为200GPa，泊松比为0.3，屈服强度为1080MPa，切线模量为1000MPa。

借助课题组开发的螺纹结构六面体有限元网格生成软件[20-21]，建立了试验螺栓紧固系统的有限元网格模型，其中单元数为194400，节点数为208787。图2给出了整体有限元网格模型和螺栓、螺母螺纹部分的局部网格模型。模型中存在四对接触面：螺栓和螺母之间螺纹副的接触面、螺母和被连接件之间的接触面（以下简称支承面）、螺栓头和被连接件之间的接触面以及两块被夹紧件之间的接触面。对这四对接触面均分别定义法向和切向接触模型，其中摩擦因数取为0.15。

图1 螺栓连接结构示意图

Fig.1 Schematic diagram of bolted joints

图2 螺栓连接结构有限元模型

Fig.2 Finite element model of bolted joints

螺栓的拧紧过程可以看作是一个准静态过程，因此采用静力学求解器。为模拟螺母拧紧过程，计算时采用了两步加载。第一载荷步施加顺时针旋转角0.5rad以实现螺母的拧紧作用，达到给定转角后保持一段时间，然后在第二载荷步释放拧紧时的加载力矩，线性卸载至0。预紧单元法需要在光杆段设置一截面为预拉截面，定义拉伸方向，在截面处生成预紧单元，指定螺栓的预紧力即可[22]。接触设置与转角法相同，将预紧单元法的预紧载荷与转角法加载得到的预紧力控制一致。下面对两种加载方法的结果进行讨论分析。

表1 主要的尺寸参数

2 转角法分析

2.1 扭拉关系分析

拧紧过程中加载扭矩与产生的预紧力之间的关系是螺栓预紧过程的一个重要特征，根据螺纹结构的几何特点和力学分析，可以将该过程等效为斜面滑块模型，得到扭拉关系式(1)，其中为扭矩系数[23]

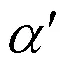
假设支承面上的压力为均匀分布，则有

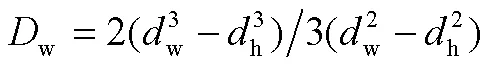
其中，h为螺栓孔内径、w为支承面的接触外径。

根据理论分析可知，扭矩与预紧力近似成线性关系。有限元仿真结果如图3所示，在加载段扭矩线性加载，预紧力也线性增加，加载段结束达到最大20.84kN；保持段转角保持不变，预紧力也保持稳定；载荷步2的卸载段，转角略有下降，即螺母轻微回转，预紧力略有下降，最终为20.76kN。

图3 随加载历程的预紧力和转角变化

Fig.3 The preload and rotation angle change with the loading process

2.2 拧紧角分析

实际装配过程中，由于各接触面有一个初始贴合的过程，此时拧紧角与预紧力呈非线性关系。本文只考虑贴合过程后的线性段。由于螺栓头部固定，拧紧角度即为螺母的旋转角度。预紧过程螺栓受拉，螺母和被夹紧件受压，由于螺母的刚度相对较大，可忽略螺母的压缩量，则有

式中，b、c分别为螺栓和被连接件的刚度。

根据德国工程师协会VDI2230标准[24]，可以将螺栓等效为几段圆柱串联，如图1所示，可分为螺栓头、螺栓光杆段、螺纹未啮合段、螺纹啮合段，对每段分别计算刚度再求得螺栓总刚度为

其中，b为螺栓的弹性模量，A为各段的等效横截面积。被连接件的刚度受其总厚度、直径、半顶角的影响，其压应力在一定范围内呈应力锥分布，其半顶角及刚度计算公式为

其中，为半顶角，为被夹紧件的外径，0为被连接件的弹性模量。

刚度和螺母拧紧角度的仿真和理论解对比见表2。通过仿真计算出的b、c可以反求出一个拧紧角度，但会与加载设置的拧紧角度有所不同。这是由于螺栓和被连接件各位置的变形并不相同，仿真得到的计算刚度是在主要变形位置取平均所得，存在一定误差。

表2 螺栓连接刚度和螺母拧紧角度

3 两种预紧力加载方法结果对比

3.1 扭矩分量对比

预紧单元法与转角法的受力有明显差异，下面以斜面滑块模型，对螺母进行受力分析，如图4所示。

图4 两种预紧方式的受力分析

Fig.4 Force analysis of two preloading methods

转角法模拟实际转动过程，螺栓相对螺母向上运动，螺纹面上的扭矩分量t、p方向相同。且螺纹面上的摩擦为滑动摩擦力，方向与运动方向相反，摩擦力和压力的向分量tsz、tnz方向相反。而预紧单元法螺栓螺母没有发生宏观的相对滑动，螺栓相对螺母有向下运动的趋势，此时的t与p方向相反，大小相等，合扭矩为0。摩擦力和压力的向分量方向相同。由于摩擦力和压力的向分量合力即为预紧力，则预紧单元法压力的向分量小于转角法，其法向接触应力小于转角法。

对转角法螺母所受扭矩进行分析，根据扭矩系数对应的三项，可以将拧紧力矩分解为三个分力矩：支承面上的摩擦力矩w，螺纹配合面上的摩擦力矩t，螺纹配合面上的正压力所形成的力矩p，也即由于螺距产生的扭矩[25]

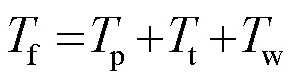
有限元软件可以直接提取得到接触面的法向和切向扭矩，仿真得到加载扭矩和各分力矩随加载历程的变化如图5所示，可以看到在载荷步1的加载段，各分力矩与加载扭矩成线性关系。当加载扭矩逐渐卸载时，Tw将明显下降。当Tf

Fig.5 Torque variation under rotation angle method

载荷步1结束时刻仿真与理论值对比见表3，此时加载扭矩为34.89N·m。仿真结果与理论解相对误差在3%以内。

表3 拧紧过程仿真与理论值对比

仿真得到预紧单元法的各扭矩如图6所示，加载完成时p=3.81N·m，略小于转角法。由p可以求出摩擦力和压力的向分量

得

而对转角法，这两个分量分别为21kN，-0.24kN。

Fig.6 Torque components of preload element method

3.2 应力分布对比

转角法卸载阶段结束后的应力如图7所示，图7 a)为螺栓的VonMises应力分布，纵向应力分布近似为轴对称，螺栓螺杆中心区域应力较小，在螺纹牙根部有明显的应力集中现象。图8、图9为螺纹牙和横截面上的应力分布，可以看出螺纹小径应力较大，即对应螺栓的螺纹牙根部，而螺栓的螺纹牙顶、螺母的螺纹牙根部应力较小。结合螺栓螺母的装配位置，以支承面为起始位置，沿轴向每移动一个螺距距离记为一圈啮合螺纹。螺栓最下面几圈的螺纹牙根部等效应力最大，这些螺纹包括未啮合螺纹和啮合螺纹的前几圈，未啮合螺纹牙不发生接触，啮合螺纹的前三圈承力较大，这些位置的轴向拉力都较大，导致VonMises应力较大，是容易发生强度破坏的位置。

图7 转角法的应力分布

Fig.7 Stress distribution of rotation angle method

图8 螺纹牙上的应力

Fig.8 Stress distribution on thread

图9 横截面上的应力分布

Fig.9 Stress distribution on cross section

转角法的法向接触应力分布如图10所示，可以看到只有螺栓的螺纹下表面有接触应力，只有该区域和螺母的螺纹上表面发生了接触，其他区域并没有接触。如图11定义一条沿螺纹面螺旋上升的路径，得到该路径上节点的法向接触应力分布曲线，如图12所示。第一圈螺纹开始接触应力较小，并迅速增大达到最大值，之后随着轴向位置增加，法向接触应力不断减小。

图10 法向接触应力分布

Fig.10 Normal contact stress distribution

图11 路径定义

Fig.11 Path definition

图12 定义路径上的接触应力分布

Fig.12 Contact stress distribution on the path

预紧单元法的VonMises等效应力、扭转切应力云图如图13所示。与图7对比可知，预紧单元法的扭转切应力远远小于转角法，最大VonMises应力略大于转角法。但由于轴向拉力是主要影响因素，VonMises应力相差不大。对于一般的以合金钢为材料的螺栓，可以采用第四强度准则进行强度校核分析，因此可以使用预紧单元法进行强度计算，提高计算效率。但对于松动问题，必须了解两种方法的加载方式带来的差异，预紧单元法不能准确模拟螺栓的拉扭复合作用，受力状态、接触状态的不同会影响松动过程的计算。

图13 预紧单元法的应力分布

Fig.13 Stress distribution of preloaded element method

3.3 载荷分布对比

由Yamamoto法[7]得到螺栓的螺纹啮合部分的轴向载荷分布公式为

式中

式中，b、n为螺栓和螺母的横截面面积；b、n为螺栓和螺母的弹性模量，b、n分别为外螺纹和内螺纹的刚度系数。提取不同横截面上的轴向力，相距一个螺距的横截面的轴向力之差即为一圈螺纹牙上的承力。对比各圈螺纹牙的载荷占比如图14所示。同理可以得到不同加载方式下轴向载荷的分布，如图15所示。

图14 轴向载荷分布占比

Fig.14 Proportion of axial load distribution

图15 轴向载荷分布

Fig.15 Axial load distribution

可以看出，两种加载方式啮合螺纹承受的轴向载荷分布相似，沿轴向先迅速增大，达到峰值后逐渐减小。在第二圈载荷占比达到最高，但第一圈载荷占比明显低于理论值。文献[26]中也得到了相似结论。这是因为我们以支承面为起始点，由图10、图12所示的接触应力分布可知，第一圈螺纹起始段的接触并不完全，只有部分面积有接触压力，且接触应力沿向迅速增大。起始段啮合面积小，接触应力小，承受的轴向载荷偏小，而理论认为各圈螺纹的啮合状态相同，导致载荷占比第一圈最大。后几牙的分布规律相似，占比都不断减小。前三牙承载仍然是轴向载荷的主要占比。

同理，得到横截面上的，方向的受力分布，如图16所示，图中F、F分别为单位长度横截面上所受的沿和方向的分力，F为其合力。预紧单元法的面力远小于转角法，两种方法的曲线都呈衰减的简谐分布，一个周期对应一个螺距距离。合力F变化趋势与轴向载荷类似，随着轴向位置增加先增大后减小，但方向随位置不断变化。分力分布的周期性与螺纹形状的有关。每个高度只有螺纹啮合部分承力。而从横向看，由于螺旋升角的影响，螺纹的横截面并不是严格绕轴的轴对称，横截面是由小径、中径、大径三段圆弧组成，小径的位置随着轴向位置的增大绕着轴转动。可以发现其合力方向指向该高度上的螺牙小径所在方向，因此合力方向也就随之转动。由于力的简谐分布，使得整个螺纹牙的横向力不断相互平衡抵消，而不是像轴向载荷累加，因此对于整个螺栓，其所受横向力很小，只有轴向拉力是主要因素。

图16 横截面内的横向力分布

Fig.16 Transverse force distribution in cross section

4 结束语

螺栓的预紧过程是研究螺栓强度和松动过程的关键。本文考虑了螺纹细节，建立了精细的六面体结构化网格模型，对比了两种不同的预紧力加载方式，结论如下：1）基于转角法仿真模型，可以准确模拟标准螺栓的拧紧过程，得到螺栓受力情况、应力分布以及变形情况，并得到扭矩-预紧力-转角三个工程中的重要参数之间的关系，与经典扭拉关系式吻合，为今后一些特殊螺纹连接（如高锁螺母、楔形螺母）的扭拉关系、转角关系研究奠定了基础。2）对比了转角法和预紧单元法，结果表明对于强度校核，为了提高计算效率可以采用预紧单元法，但是预紧单元法没有准确考虑螺栓预紧过程中的切向载荷作用，两种方法的受力状态有所差别，对于松动问题的研究，仍有必要基于转角法得到螺栓螺母的初始受力状态和接触状态。

[1] 王桢, 张京东, 丁晓宇, 等.螺纹连接结构松动分析方法研究[J].强度与环境, 2020, 47(6): 8-14.[Wang Zhen, Zhang Jingdong, Ding Xiaoyu, et al.Technique research on looseness analysis of threaded fasteners [J].Structure & Environment Engineering, 2020, 47(6): 8-14.]

[2] 濮良贵, 陈国定, 吴立言.机械设计(第九版)[M].北京: 高等教育出版社, 2013.

[3] 吴南星, 成飞, 廖达海, 等.高锁螺栓连接力学参数关系的实验研究[J].机床与液压, 2017, 45(1):77-80.[Wu Nanxing, Cheng Fei, Liao Dahai, et al.Experimental study on the relationship between the mechanical parameters of hi-lock bolt connection [J].Machine Tool & Hydraulics, 2017,45(1): 77-80.]

[4] Chen D, Ma Y, Hou B.Tightening behavior of bolted joint with non-parallel bearing surface[J].International Journal of Mechanical Sciences, 2019: 153-154.

[5] 侯博文.真实接触表面形貌下螺栓连接结构的力学性能[D].大连理工大学, 2020.

[6] 徐卫秀, 王淑范, 杨帆, 等.考虑螺纹细节的螺栓预紧过程仿真分析研究[J].宇航总体技术, 2018, 2(5): 50-56.[Xu Weixiu, Wang Shufan, Yang Fan, et al.Study of bolt pre-tightening process based on simulation with thread details [J].Astronautical Systems Engineering Technology, 2018, 2(5): 50-56.]

[7] Sopwith D G.The distribution of load in screw threads[J].Iust.Mech.Engrs.Appl.Mech.Proc,1948, 159: 373-383.

[8] 山本晃.螺纹联接的理论与计算[M].上海: 上海科学技术文献出版社, 1984.

[9] 陈海平, 曾攀, 方刚, 等.螺纹副承载的分布规律[J].机械工程学报, 2010,46(9): 171-178.[Chen Haiping, Zeng Pan, Fang Gang, et al.Load distribution of bolted joint [J].Journal of Mechanical Engineering, 2010, 46(9): 171-178.]

[10] 李志彬.螺栓连接结构松动失效机理研究[D].大连理工大学, 2019.

[11] 江文强, 墨泽, 安利强, 等.考虑螺纹柔性的螺栓连接临界松动载荷计算方法[J].机械工程学报, 2020, 56(15): 238-248.[Jiang Wenqiang, Mo Ze, An Liqiang, et al.Computing method of bolted joint critical loosening load with flexible thread [J].Journal of Mechanical Engineering, 2020, 56(15): 238-248.]

[12] 贺李平, 任雪梅.螺栓联接的有限元建模方法研究[J].北京理工大学学报,2020,40(12):1275-1281.[He Liping, Ren Xuemei.Study on finite element modeling method of bolted joints [J].Transactions of Beijing Institute of Technology, 2020, 40(12):1275-1281.]

[13] Liao Ridong, Sun Yujuan, Zhang Weizheng.Nonlinear analysis of axial-load and stress distribution for threaded connection [J].Chinese Journal of Mechanical Engineering, 2009, 22(6): 869-875.

[14] Gong Hao, Liu Jianhua, Ding Xiaoyu.Study on the mechanism of preload decrease of bolted joints subjected to transversal vibration loading [J].Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2019, 233(12): 2320-2329.

[15] Fukuoka Toshimichi, Nomura Masataka.Proposition of helical thread modeling with accurate geometry and finite element analysis[J].Journal of Pressure Vessel Technology, 2008, 130(1).

[16] 徐超, 余绍蓉, 郑晓亚, 等.机械螺栓法兰连接的有限元力学模型比较研究[J].机械设计与制造, 2009(6): 37-39.[Xu Chao, Yu Shaorong, Zheng Xiaoya, et al.Comparative evaluation of finite element models for mechanical structures with bolted joints [J].Machinery Design & Manufacture, 2009(6): 37-39.]

[17] 王灿, 丁振军, 韩帅帅, 等.基于精确螺纹建模的螺栓紧固工艺研究[J].工程机械, 2020, 51(2): 31-39.[Wang Can, Ding Zhenjun, Han Shuaishuai, et al.Research of bolt fastening process based on accurate thread modeling [J].Construction Machinery and Equipment, 2020, 51(2): 31-39.]

[18] 王传华, 王文莉, 林清源, 等.基于精确建模的横向振动工况下螺栓松动机理研究[J].宇航总体技术, 2018, 2(4): 43-51,64.[Wang Chuanhua, Wang Wenli, Lin Qingyuan, et al.Study on bolt loosening mechanism in vibration condition based on precise model [J].Astronautical Systems Engineering Technology, 2018, 2(4): 43-51,64.]

[19] 胡阳, 姜东, 王旻睿, 等.横向载荷作用下螺栓连接松动过程研究[J].振动、测试与诊断,2020,40(6):1091-1098.[Hu Yang, Jiang Dong, Wang Minrui, et al.Study on loosening process of bolted joints under transverse load [J].Journal of Vibration, Measurement & Diagnosis, 2020, 40(6): 1091-1098.]

[20] 侯世远.螺纹联接松动机理研究[D].北京理工大学,2015.

[21] 邬杰.螺纹连接结构横向松动寿命预测模型研究[D].北京理工大学, 2019.

[22] 陈岩.螺栓松动的失效机理以及对整体结构力学行为的影响研究[D].大连理工大学,2019.

[23] Motosh Nabil.Load Distribution on threads of titanium tension nuts and steel bolts[J].Journal of Engineering for Industry, 1975, 97(1): 162-166.

[24] Ingenieure V D .Systematic calculation of high duty bolted joints joints with one cylindrical bolt [J].Berlin : VDI,2003:171.

[25] Nassar Sayed A, Yang Xianjie.Novel formulation of the tightening and breakaway torque components in threaded fasteners [J].Journal of Pressure Vessel Technology, 2007, 129(4): 653-663.

[26] 潘瑞鹏.摩擦系数对螺栓连接紧固性能的影响研究[D].北京理工大学, 2020.

Finite Element Simulation of Bolt Pre-Tightening Process

GUI Xue-wen ZHANG Jing-dong LIAO Ri-dong

(School of Mechanical and Vehicular Engineering，Beijing Institute of Technology, Beijing 100081, China)

The pre-tightening process is directly related to the strength calculation and loosening analysis of bolted joints.However, the pre-tightening process of bolts is a complex nonlinear problem.At present, the understanding of the stress state, contact state and the differences of different loading methods of bolts after pre-tightening is still unclear.In this paper, a fine bolt hexahedron mesh model is established, and two different loading methods, rotation angle method and preload element method, are simulated.Based on the rotation angle method, the relationship among torque, angle and preload is studied, which lays a foundation for the study of some special threaded connections.The stress and contact state of bolts after preloading under the two loading methods are compared and analyzed.The results show that the rotation angle loading method used in this paper can accurately simulate the tightening process of bolts, and the preloading element method can only simulate the distribution of axial force, but cannot accurately consider the influence of tangential force.

Bolted joints; Pre-tightening process; Relationship between the preload and tightening torque

TH122

A

1006-3919(2021)06-0009-08

10.19447/j.cnki.11-1773/v.2021.06.002

2021-06-23；

2021-09-17

科学挑战专题项目（TZ018007）

桂学文（1998—），男，硕士研究生，研究方向：动力机械结构强度；（100081）北京市海淀区中关村南大街5号北京理工大学发动机西楼301.