基于不确定性的飞行器总体设计应用

池元成 刘闻 李晶 王长庆

基于不确定性的飞行器总体设计应用

池元成 刘闻 李晶 王长庆

(中国运载火箭技术研究院, 北京 100076)

飞行器总体设计在飞行器研制过程中具有重要地位。由于工程实际中存在的不确定性因素，需要在传统确定性问题的基础上，考虑不确定性因素的影响。因此，通过分析确定性优化问题和不确定性优化问题的流程，结合飞行器总体设计，分析了确定性优化问题中不确定性因素的影响，并根据影响结果，建立了不确定性优化问题，在满足约束条件下，获得了不确定性条件下最优解，显著提高了满足约束的概率。

不确定性；飞行器总体设计；差分进化算法；优化设计

0 引言

飞行器总体设计是一项复杂系统工程，根据战术技术要求和技术发展实际状况，对飞行器及其组成飞行器的各系统进行综合、协调、研究、设计与试验的过程，直接关系到飞行器的综合性能、研制周期和研制经费等，往往要经过多次反复设计，才能得到一个综合性能最佳的飞行器总体技术方案，因此在飞行器研制过程中具有重要地位[1]。传统的飞行器总体设计过程中，往往忽略不确定因素，或者用参数的较大包络去涵盖不确定性因素的影响，采用确定性问题获得飞行器初始方案，再通过多次迭代获得可靠的总体方案。不确定性存在于飞行器设计的各个阶段，按照不确定性的来源可分为随机不确定性和认知不确定性[2]。在飞行器总体设计过程中，识别不确定性因素并充分考虑不确定性影响，从而降低综合性能对不确定影响的敏感程度，提高综合性能的稳健性和可靠性，国内外在相关领域已开展了研究应用[3-7]。飞行器设计优化是从一组可行方案中选择最佳可行方案的过程。即对于优化问题，通过优化算法求解最优解。由于工程实际中存在的不确定性，不可能追求满足要求的最优解，而是退而求其次，追求满足要求的次优解。本文对某飞行器总体方案进行了优化设计，再利用不确定性方法开展了总体可靠性设计，并对结果数据进行了分析。

1 不确定性优化问题

传统的确定性优化问题可描述为

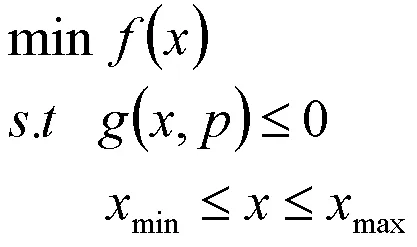
其中，f为目标函数，g为约束条件，x为设计变量，p为设计参数。确定性优化流程是由优化算法生成设计变量初始值，由设计变量计算目标函数和约束条件，在判断是否满足停止条件，不满足则返回，继续由优化算法生成下一步设计变量初始值，如此往复，直到满足停止条件，选取最优解，如图1所示。

然而，在工程实际中设计变量和设计参数中或多或少的存在不确定性，如飞行载荷、材料属性、制造工艺等，即数学上服从某种分布的随机变量。此外，由于约束条件的限制，工程实际确定性优化问题的优化解往往在约束边界上，即起作用约束的存在，使得确定性优化问题的优化解容易违反约束，即违反约束的概率较高，导致优化解不可靠，这也是实际工程上对优化设计方法不可信的原因之一。

因此，工程中迫切需要研究不确定性优化设计方法，在建模过程中引入不确定性因素，通过不确定性分析，对确定性优化解进行适当调整，也就是以较高的概率不违反约束条件，从而获得满足工程实际需求的较优解。当考虑设计变量和设计参数的不确定性时，不确定性优化问题可描述为

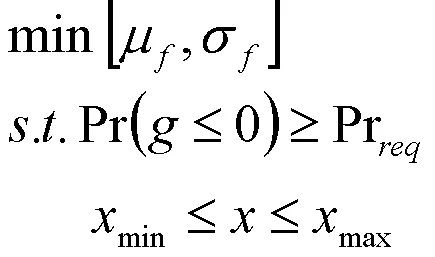
其中，μ为均值，σ为标准差，Pr为概率。不确定性优化流程如图2所示。由图1和图2可知，不确定性优化流程是双层嵌套的流程，相比于确定性优化流程，不确定性优化流程多了不确定性分析的循环流程，用于计算概率。不确定性分析过程中，对于数值计算问题，一般采用蒙特卡洛计算。根据模型的复杂度，可选择不同的不确定性量化方法进行分析，如对于计算复杂度高的模型，可使用近似模型代替复杂模型，提高计算效率。

2 差分进化算法

差分进化（Differential Evolution，DE）[8,9]算法作为群智能算法的代表算法之一，能够实现全局优化。DE不同于遗传算法（Genetic Algorithm，GA）使用二进制编码，而是直接采用实数编码，省去了不必要的麻烦。DE通过父代个体间的简单数学组合来产生不同的候选个体，再通过比较个体间的函数适应值的优劣关系确定候选个体是否取代父代个体。现已证明DE较其他现有的进化算法是有效的、鲁棒的。由于DE简单易实现，可调参数少，目前在很多领域的复杂优化问题求解中得到了应用。

DE算法基于父代个体间的差异，经变异、交叉和选择产生子代，根据在搜索空间内随机选取的两个个体向量的差值与第三个随机选取的个体向量的加权求和来实现群体变异，然后通过比较由交叉算子生成的个体和相应父代个体的函数值优劣来保存优秀个体，如此反复迭代，不断进化。定义维搜索空间内，存在种群数为的个体i=(x1,x2,…,x) (=1,2, …,)，此时变异个体V=(v1,v2, …,v)通过式(3)产生

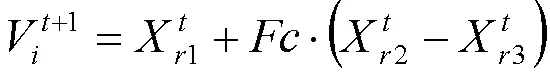
式中，1、2和3是异于且互不相同的[1,]之间的整数；为缩放比例因子；为当前迭代步数。式(3)中，X1称为基向量，(X2-X3)称为差分向量。

父代个体X和变异个体V依据交叉概率生成实验个体U=(u1,u2, …,u)

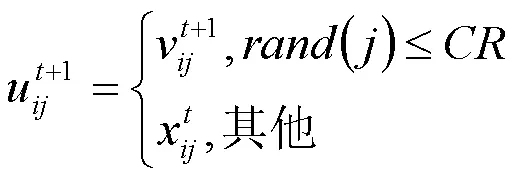
式中，()是[0,1]之间的均匀随机分布数。

对于最小化问题，交叉后的个体U+1和父代个体X依据式(5)进行选择操作，生成子代个体X+1

式中，为求解问题的目标函数值。

3 不确定性优化设计方法

结合上述的内容，对于工程实际问题，不必直接采用不确定性分析方法完成优化设计，可采用如下的步骤完成不确定性分析与优化。

步骤1：按式(1)选定目标函数和约束条件，确定设计变量，即设定确定性优化问题；

步骤2：按图1所示的流程求解确定性优化问题，获得满足约束的最优解；

步骤3：对于最优解完成不确定性分析，若满足则选择最优解完成方案设计；否则，转步骤4；

步骤4：按式（2）设定不确定性优化问题；

步骤5：按图2所示的流程求解不确定性优化问题，获得满足约束的最优解，通过分析作为最终方案。

4 优化模型与结果分析

某飞行器总体设计涉及动力、控制、结构等多个专业，本文通过结构设计矩阵梳理了各专业之间的参数传递关系与具体传递参数，并搭建了飞行器总体方案设计流程，其设计结构矩阵如图3所示。

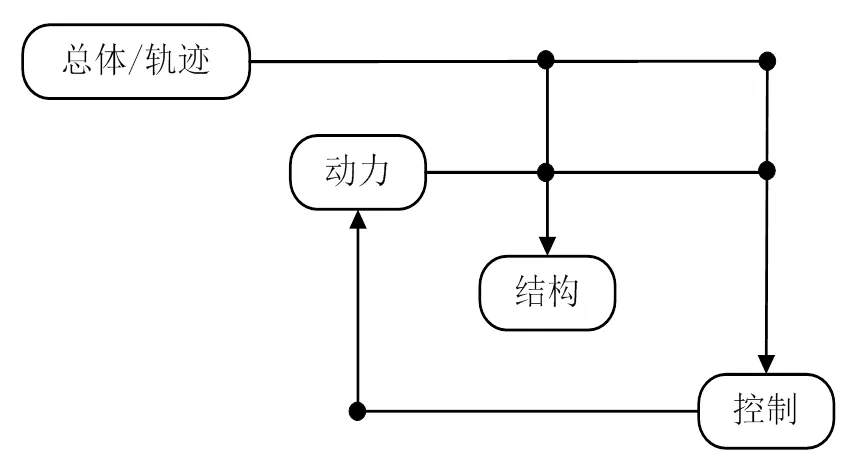
图3 总体设计结构矩阵

为了达到设计要求，以飞行距离（）最大作为优化目标，构建了确定性优化问题

（6）

其中，为设计变量，选取了燃料质量等3个关键变量。为简化研究，文中令三个优化设计变量均服从正态分布，变异系数为0.005，如表1所示。

表1 优化设计变量

利用差分进化算法完成优化求解后，得到了表2所示的最优解。

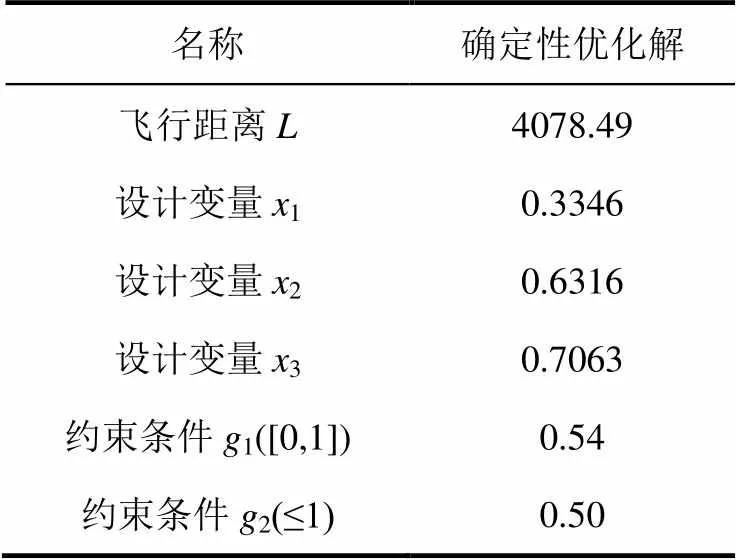
表2 确定性优化结果

由表2可知，最优解的约束条件离边界非常接近，通过分析可知，违反约束条件1的概率为0.46，违反约束条件2的概率为0.50，最优解的可靠性相对较低，采用风险较大。

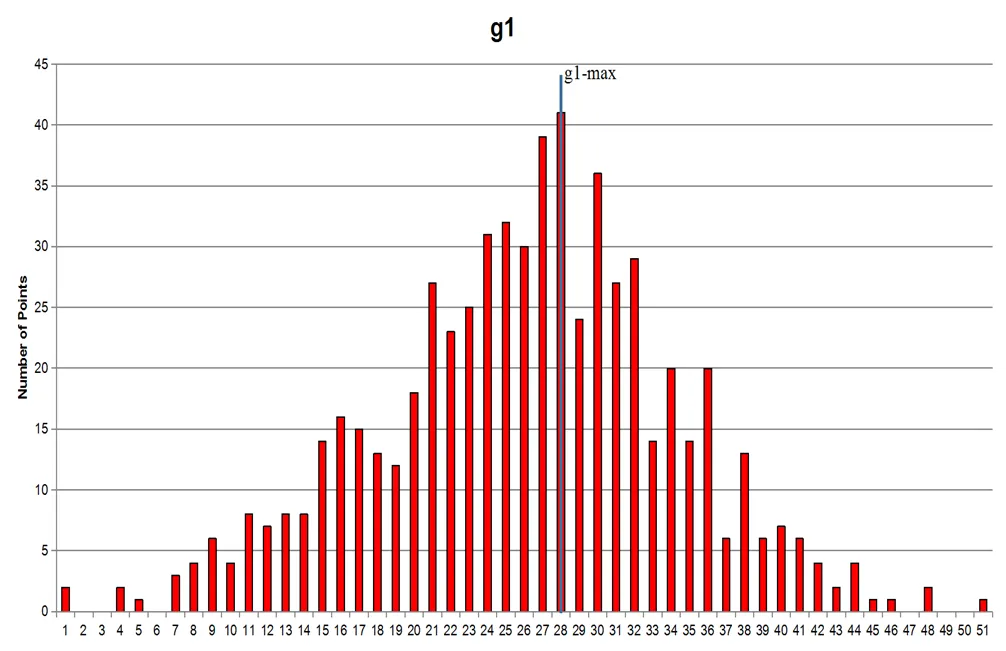
图4 约束条件g1概率分布

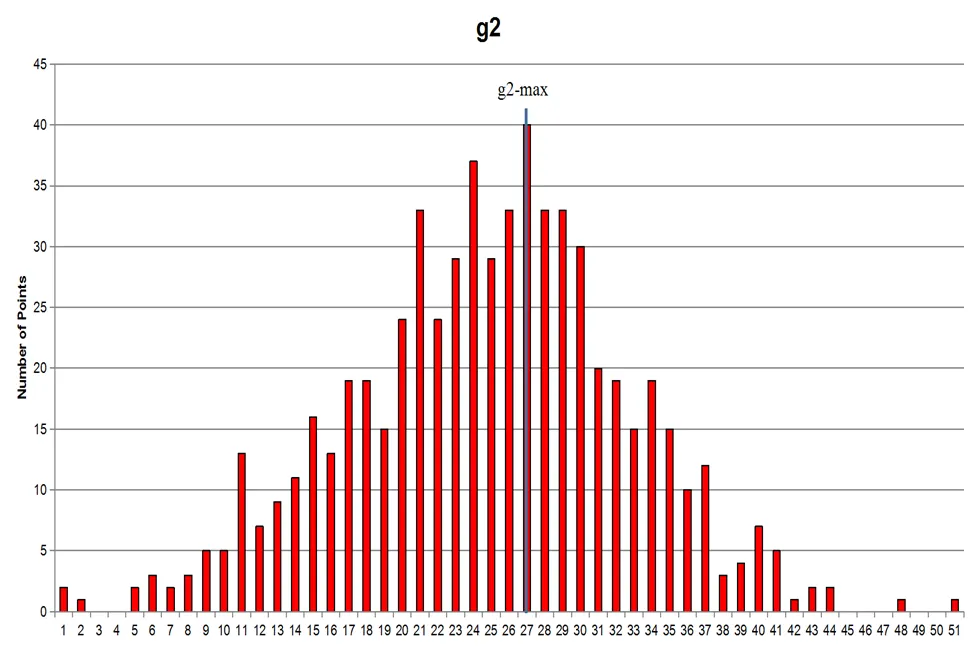
图5 约束条件g2概率分布

为此，将上述问题转化为不确定性优化问题

(7)

其中，满足约束的概率大于90%。

考虑不确定性条件下，利用差分进化算法完成优化求解后，得到了表3所示的最优解。

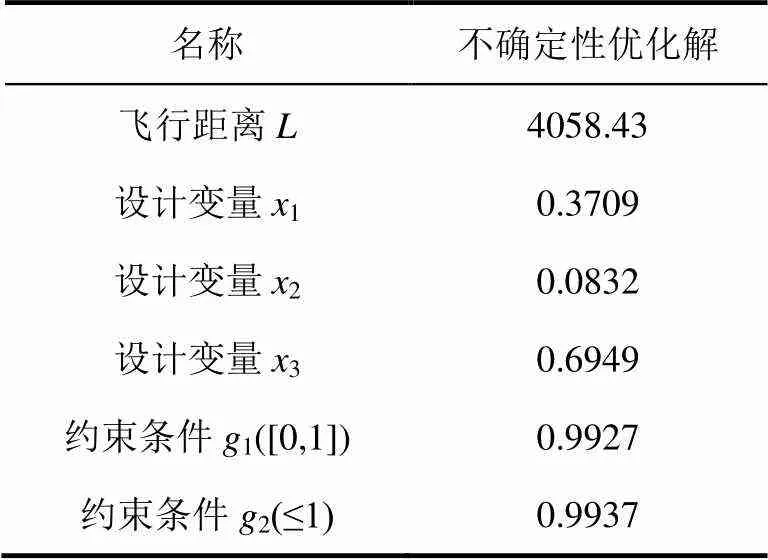
表3 不确定性优化结果

由表3可知，考虑不确定性的条件下，最优解相比确定性优化解，稍差0.05%，然而约束条件1和约束条件2的违反概率分别降低为0.0073和0.0063，可知最优解可靠性提高显著，可以采用。

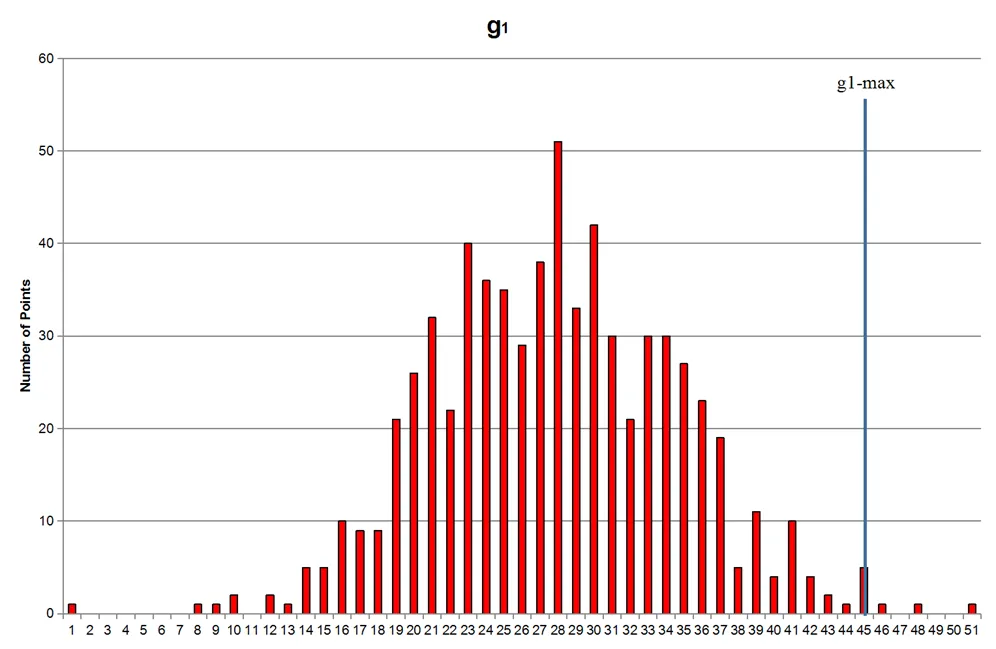
图6 约束条件g1概率分布

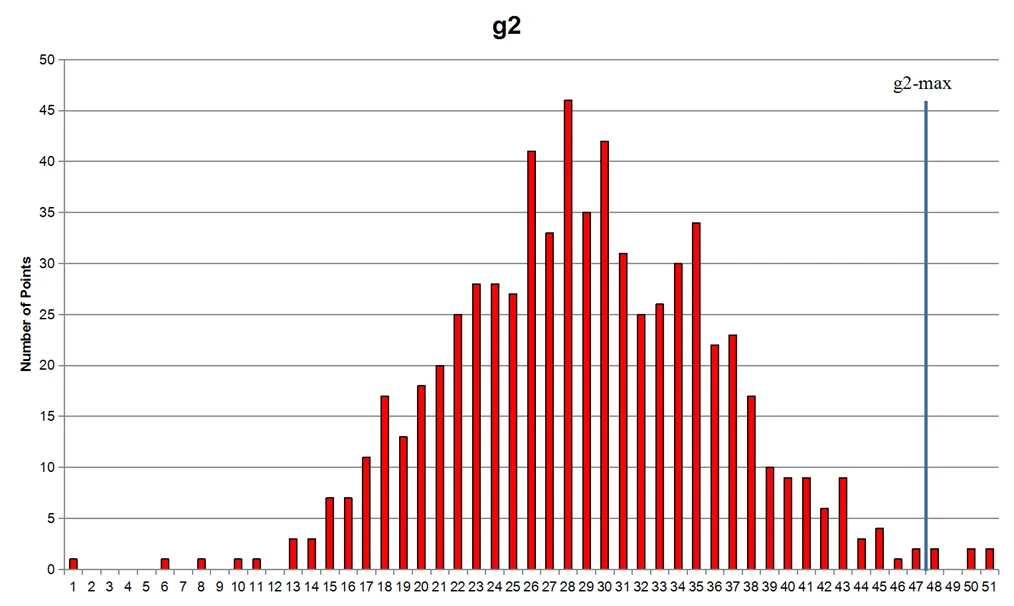
图7 约束条件g2概率分布

3 结论

本文以某飞行器总体设计为对象，利用不确定性优化设计方法对其进行了优化分析，获得了满足约束条件的较优解。然而，在工程实际中还需要在以下几个方面开展深入的研究。

1）飞行器总体设计过程是一个多轮次迭代的过程，飞行器总体方案由粗到细，在使用不确定性方法时，还需要进一步分析在什么环节考虑哪些不确定性因素；

2）飞行器总体设计各学科专业建模时，要充分考虑不确定性，除了随机不确定性，更要关注认知不确定性，对工程实际问题完整描述；

3）学科专业模型的精度或置信度要提高，当模型精度较低时，计算结果会覆盖不确定性因素的影响；

4）当优化问题中涉及的不确定性因素较多时，要事先完成不确定性参数灵敏度分析；当模型计算量较大时，要考虑构建近似模型。

[1] 侯世明.导弹总体设计与试验[M].北京: 宇航出版社, 1996.

[2] 陈小前.飞行器不确定性多学科设计优化理论与应用[M].北京: 科学出版社, 2013.

[3] 李晓斌, 张为华, 王中伟.固体火箭发动机装药不确定性优化设计[J].固体火箭技术, 2006, 29(4): 269-273.[Li Xiaobin, Zhang Weihua, Wang Zhongwei.Uncertainty optimization design of solid rocket motor grain [J].Journal of Solid Rocket Technology, 2006, 29(4): 269-273.]

[4] 王宇, 余雄庆.考虑不确定性的飞机总体参数优化方法[J].航空学报, 2009, 30(10): 1883-1888.[Wang Yu, Yu Xiongqing.Optimization method for aircraft conceptual design under uncertainty, 2009, 30(10): 1883-1888.]

[5] Fuchs M, Neumaier A, Girimonte D.Uncertainty modeling in autonomous robust spacecraft system design[J].PAMM, 2007, 7(1):2060041-2060042.

[6] Green L L, Lin HZ, Khalessi M R.Probabilistic methods for uncertainty propagation applied to aircraft design [R].AIAA-2002-3140, 2002.

[7] 沈凤霞.力学环境试验测量不确定度分析[J].强度与环境, 2010, 37(1): 58-64.[Shen Fengxia.Measurement uncertainty analysis of dynamic environment test [J].Structure & Environment engineering, 2010, 37(1): 58-64.]

[8] Storn R, Price K.Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces, TR-95-012 [R].Berkeley: International Computer Science Institute, 1995.

[9] Storn R, Price K.Minimizing the real function of the ICEC’96 contest by DE [C].IEEE International Conference on Evolutionary Computation, 1996: 842-844.

Application of Aircraft Overall Design based Uncertainty

CHI Yuan-cheng LIU Wen LI Jing WANG Chang-qing

(China Academy of Launch Vehicle Technology, Beijing, 100076, China)

The overall design of aircraft plays an important role in the process of aircraft development.Due to the uncertain factors in practical engineering, it is necessary to consider the influence of uncertain factors on the basis of traditional deterministic problems.Therefore, by analyzing the process of deterministic optimization problem and uncertain optimization problem, combined with the overall design of aircraft, the influence of uncertain factors in deterministic optimization problem is analyzed, and according to the influence results, the uncertain optimization problem is established.Under the constraint conditions, the optimal solution under the uncertainty conditions is obtained, which significantly improves the probability of meeting the constraints.

Uncertainty; Aircraft overall design; Differential evolution; Optimize design

V211.4

A

1006-3919(2021)06-0045-05

10.19447/j.cnki.11-1773/v.2021.06.007

2021-05-29；

2021-08-03

国家重点研发计划项目（2020YFB1709400）

池元成（1981—），男，博士，高级工程师，研究方向：飞行器总体设计与优化；（100076）北京9200信箱38分箱.