基于非线性接触刚度的铰接/锁紧结构动力学建模方法
任浩源 王毅 王亮 周剑波 常汉江 蔡毅鹏 王乐 雷豹
基于非线性接触刚度的铰接/锁紧结构动力学建模方法
任浩源 王毅 王亮 周剑波 常汉江 蔡毅鹏 王乐 雷豹
(中国运载火箭技术研究院,北京,100076)
基于位移矢量方程和非线性有限元,建立了可折叠翼面局部铰接锁紧结构连接刚度求解方法,并开展翼面整体静力/振动特性的理论研究和试验验证。首先,构建了考虑可折叠翼面柔性变形和配合间隙影响的位移矢量方程;然后,对折叠翼面局部铰接结构进行静力学分析,并基于粒子群优化方法对位移矢量方程中的转动矩阵和平移矢量进行求解,获得不同载荷下铰接锁紧结构的非线性刚度;最后,将局部结构刚度值带入整体翼面结构的板-弹簧模型中,并开展静力学分析和模态分析,研究表明理论预示结果与试验结果具有较好的一致性,验证了刚度计算方法的精度和可用性。本文提出的方法对可折叠翼面锁紧结构优化设计、翼面结构动力学分析预示等均具有一定的参考性。
可折叠翼;连接刚度;静力分析;模态分析
0 引言
近年来助推滑翔型高速飞行器得到了快速发展,由于其追求超远飞行距离,故需采用高升阻比气动外形和大翼/舵面的布局形式。然而飞行器受到发射平台尺寸的约束,需要在发射前将翼/舵面折叠,发射后再择机展开[1-2]。可折叠翼的铰接/锁紧结构内部存在间隙,呈现典型的非线性力学特性,并显著影响整体翼面的结构动力学特性,因此折叠翼结构动力学分析研究在新型高速飞行器研制中将发挥越来越重要的作用。
折叠翼整体结构的建模要素多、影响大,其中铰接/锁紧结构动力学模型精度是分析的关键,因此国内外学者针对折叠翼面动特性建模问题已开展了大量理论和试验研究[3-6]。在理论研究方面,Tang等[7]和Snyder等[8]采用有限元方法对折叠翼的振动特性和颤振特性进行研究,在模型中将折叠结构等效为集中的线性扭簧,并给出了弹簧刚度和折叠角度等参数对振动特性的影响规律。Castrichini等[9]在飞机翼尖折叠结构建模中引入双线性刚度弹簧,并研究了弹簧刚度与飞行气动载荷减缓特性之间的关系。何昊南和于开平等[10-11]将折叠舵连接处的非线性特性等效为线性与非线性刚度组合扭转弹簧,并开展含间隙折叠舵在不同激励量级和间隙值组合条件下的振动分析和热气弹研究。Hu等[12-13]采用柔性多体动力学方法对可折叠翼面在变体展开过程中的气动弹性响应行为进行研究。在试验研究方面,Wu等[14]对含间隙非线性连接全动舵面的振动特性进行研究,采用子结构自由界面模态综合法和CRP方法对非线性参数进行辨识。Ma等[15]采用直接参数估计方法对折叠舵系统开展模型辨识工作,并基于相对速度和相对位移的组合多项式建立连接位置的非线性恢复力。Yang等[16]对间隙折叠舵开展风洞试验研究,给出了折叠位置的转动角度间隙对翼面颤振特性的影响规律。
目前的可折叠翼面结构动力学建模,大多先将铰接/锁紧结构简化为直接共节点和线性/非线性弹簧,然后采用反向辨识,正向建模研究较少。然而在工程研制中,需要在图纸设计阶段就对翼面整体特性进行评估,正向建立具体连接结构形式与连接刚度特性的关系对飞行器的初期设计、改进和优化至关重要。因此,本文建立了基于位移矢量方程和有限元模型的非线性连接刚度正向求解方法。针对折叠翼面局部铰接结构的连接刚度问题,从翼面整体中切出连接锁紧结构局部模型,采用静力分析获得不同载荷下连接锁紧结构的6个自由度连接刚度,再利用已获取的连接刚度开展翼面整体结构的非线性静力学分析和含预载条件下的模态分析,并基于试验结果对方法的精度和可用性进行验证。
1 模型
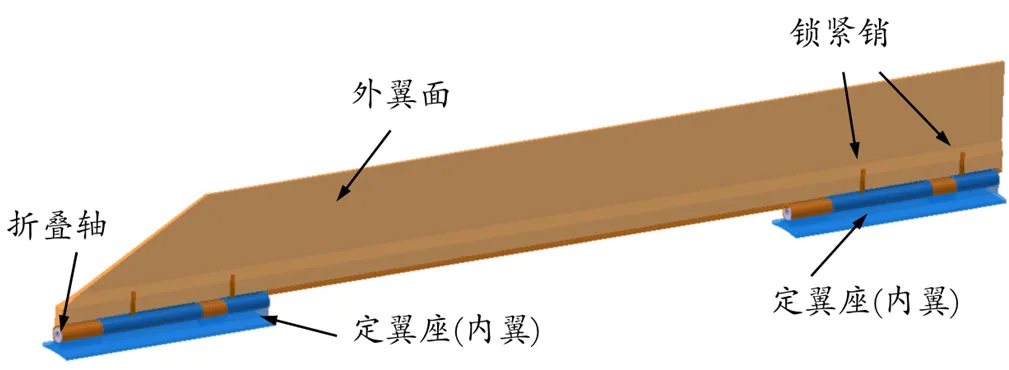
折叠翼采用翼根部折叠方式,分析模型主要由外翼面、定翼座(内翼)、折叠机构等组成,由于翼面较薄,故翼面采用实体结构,如图1所示。动翼面材料为铝合金2A14-T6,定翼座材料为钛合金TC4,折叠机构材料为钢0Cr17Ni4Cu4Nb。动翼面与定翼座通过四处铰接锁紧结构进行连接,铰接锁紧结构主要包括动翼局部结构、内翼局部结构、折叠转轴和圆柱锁紧销。先将外翼、内翼和折叠转轴组装,再通过置于外翼内部的锁紧销与内翼圆柱的键槽进行配合以对结构进行锁紧。外翼面的折叠转轴区域采用非对称结构,当翼面承担正气动升力时,通过外翼面转轴根部三角区域与内翼面的斜面进行接触配合传递弯矩;而在翼面承担负气动力时,通过外翼面内部安装的锁紧销与内翼的预置键槽接触配合传递弯矩。
2 局部连接刚度
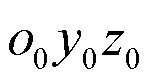
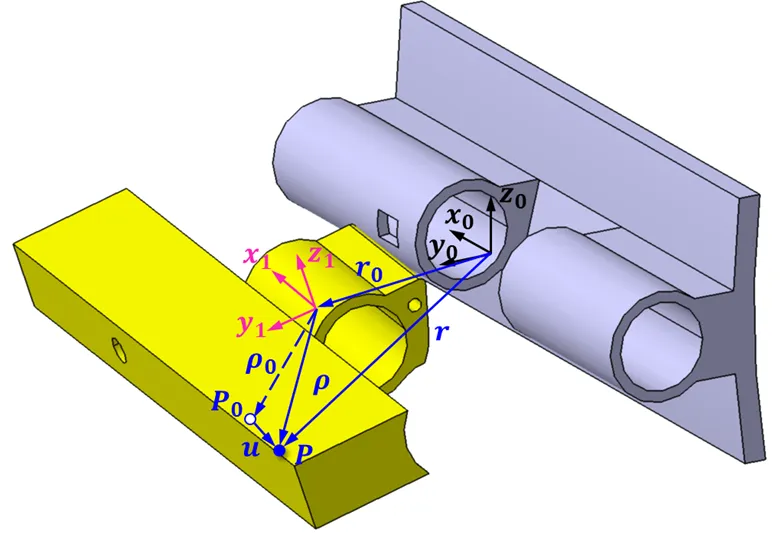
图2 坐标系及位移矢量
根据节点位移矢量方程可知,变形前后外翼面的节点位置矢量满足式(1)
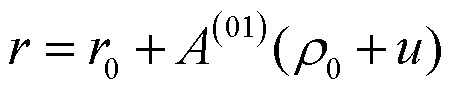
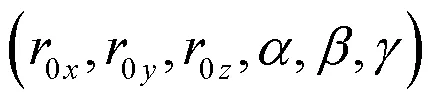
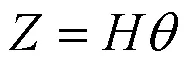

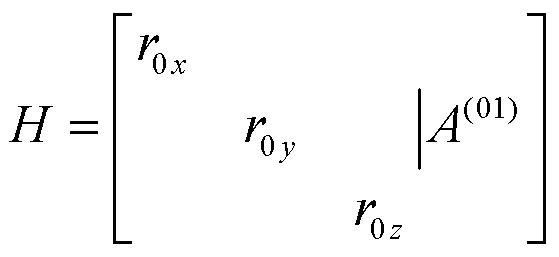
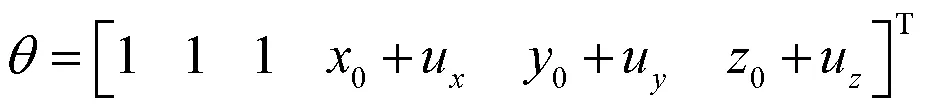
将待辨识参数直接编码,辨识误差指标函数取为
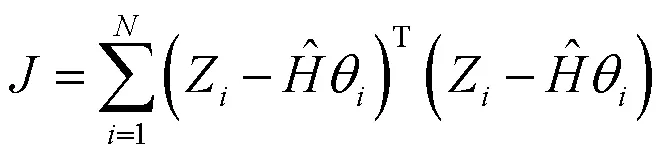
采用有限元分析软件对局部铰接/锁紧装置进行建模。由于结构形式复杂,因此利用实体单元进行建模。其中,外翼和内翼结构整体采用8节点六面体单元网格划分,在包含孔/槽的复杂区域采用6节点棱柱单元,折叠转轴区域采用四面体网格,整体网格如图3所示。
对内翼面的根部和转轴施加位移边界条件:约束翼面根部表面节点的xyz三个方向的平动自由度,约束转轴截面节点的x方向平动自由度。为了求解单个铰接锁紧结构的刚度,设计如表1所示的4种加载工况,对结构进行静力分析。

图3 网格划分
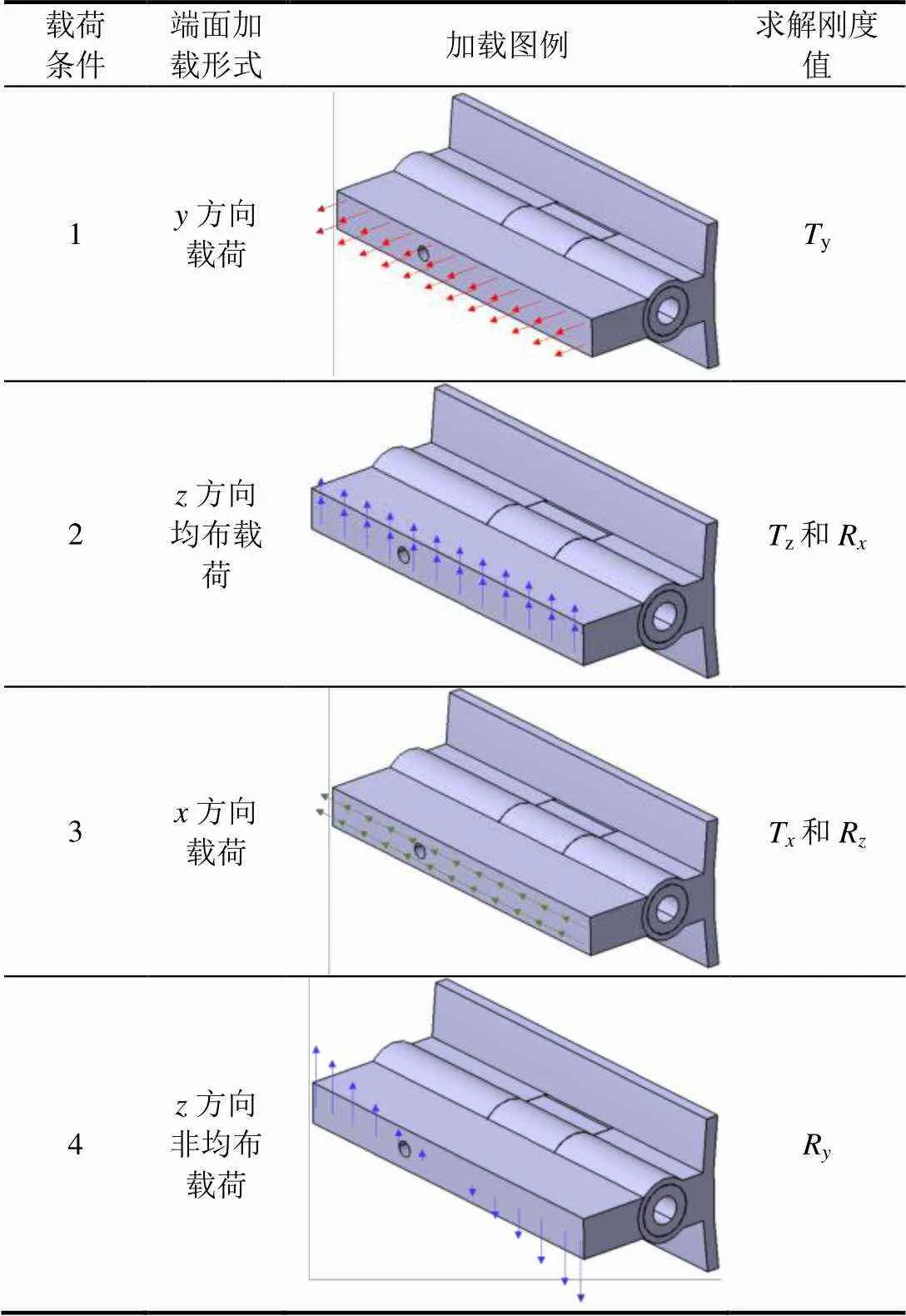
表1 加载条件
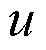
由计算结果分析可知,
1)在单一方向外载荷作用下,随载荷的增大,刚度值呈现出“双线性”和“渐刚性”两种特性。这与文献[10]和文献[14]的刚度结果具有相似的规律。文献中“双线性”模型主要基于间隙区的刚度为0,接触后刚度为线性;而“渐刚性”模型基于Hertz理论假设,接触刚度随载荷增大而增大。由于已有文献对翼面折叠建模仅考虑绕折叠轴的转动刚度,因此只能用单一的刚度形式,即双线性刚度或者渐刚性模型,而实际工程中的真实铰接/锁紧结构因其非理想化的结构形式导致同时存在两种非线性特性。
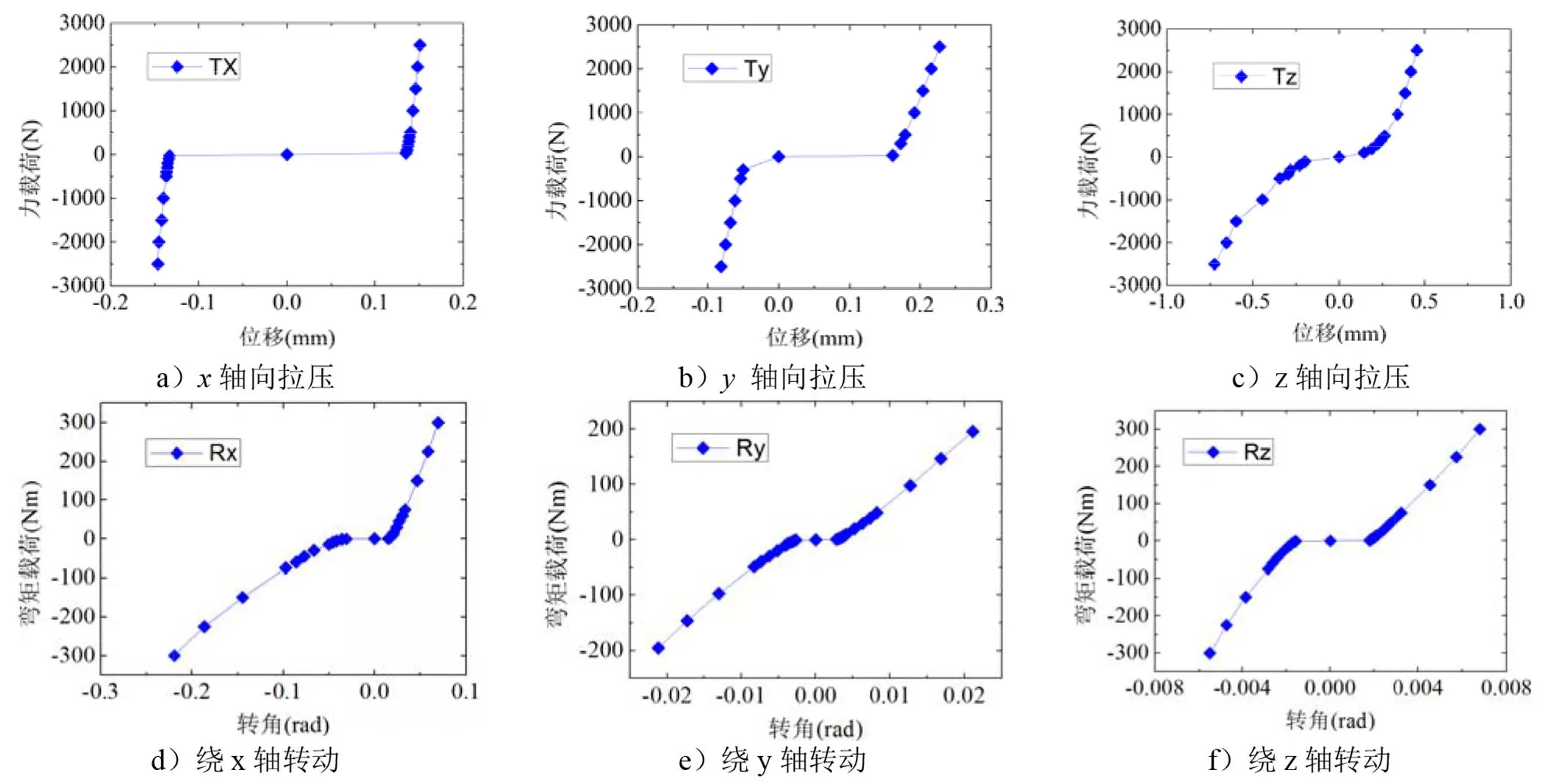
图4 局部铰接锁紧结构的载荷-位移曲线
2)通过正向加载和反向加载分析,刚度呈现非对称特性。以绕折叠轴的转动刚度R为例,其正向加载条件下的刚度大于反向加载时的刚度。这与结构形式紧密相关,正向弯矩加载为斜面配合面接触承载,受力状况更为理想,因此刚性较大;而反向弯矩加载时为销钉和键槽局部接触承载,接触区域小于正向加载条件下的接触面积,因此刚性较弱。但是R和R刚度在正反加载下基本呈现对称特性,这是由于结构存在一定的对称性。
3 翼面整体分析及试验验证
3.1 静力学计算与试验
采用有限元分析软件对翼面在静载荷下的变形进行求解。由于内翼面根部与支撑结构采用双排10个M6×20螺栓固支,边界固定刚性较强,且内翼面材质为钛合金,弹性模量显著高于外翼的铝合金材料模量,前期试算表明在有限元建模中忽略内翼面变形对结果的影响微弱。采用板单元仅对外翼进行建模,在有限元模型中不再建立铰接锁紧结构的细节模型,而是在四处转轴锁紧结构中心的坐标处添加Bush单元进行锁紧刚度的模拟,Bush单元的刚度值由上文求解的局部连接结构的载荷-位移关系曲线进行表征,最终的外翼有限元模型如图5所示。
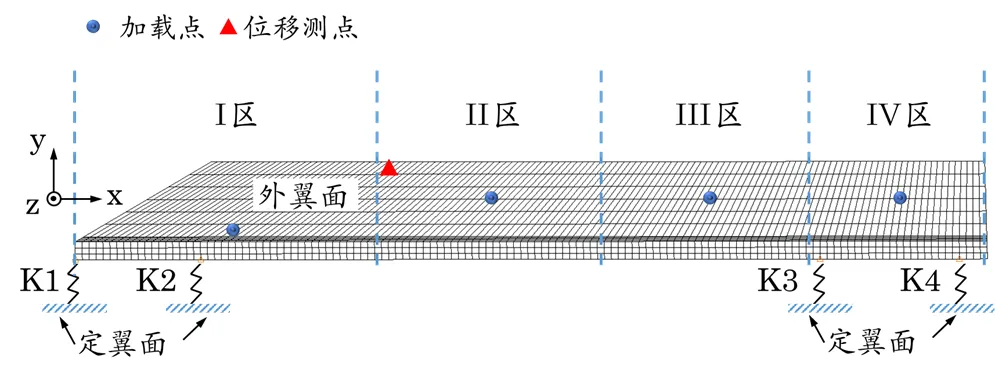
图5 外翼面板单元模模型及分区加载
采用集中载荷的方式模拟翼面在飞行过程中的分布气动载荷,并研究载荷作用下的翼面变形情况。由于前翼根弦较长,若采用全翼面单点加载的方式难以真实模拟气动情况,因此采用分区加载的方法。即将前翼分成四部分,分别将载荷(F1-F4)作用于分区压力中心处,并提取各工况条件下外翼边缘测点处Z轴方向变形量。共设计8组载荷(表2),加载方向为正向和反向加载,共计16个加载工况条件。
各工况下位移-载荷曲线的计算解与试验结果如图6所示。针对静力试验结果和计算结果进行分析可知:随着施加载荷的增大,外翼面相应的测点位移值也增大,且整体呈现“渐刚性”非线性特性。对于第8级载荷条件,正向加载下的位移测点处实测位移值为23.36mm,反向加载对应位移为30.75mm,存在拉压非线性特性,这与前文的刚度计算特性相一致。此外,试验值与计算值整体趋势一致,但位移的计算值略大于试验值,其原因是单独铰接结构由整体结构中切出,在一定程度上破坏了翼面双转动副的传力特性,导致计算刚度小于实际刚度。
3.2 模态特性计算与试验
借助前文单个铰接/锁紧结构的刚度计算结果,将载荷位移关系曲线表征的刚度带入到翼面整体模型的Bush单元中,计算在不同加载下的频率和振型,并与模态试验结果进行对比分析,如图7所示。各阶频率计算结果与试验结果如表3和图8所示,相应的振型结果如图9和图10所示。将试验结果与计算结果对比可知,计算频率与试验频率具有较好的一致性,各阶固有频率的计算值与试验值的最大相对误差在12%以内。

图6 外翼翼面位移-载荷曲线
Fig 6 Displacement-load curve of out-wing

图7 翼面模态试验现场
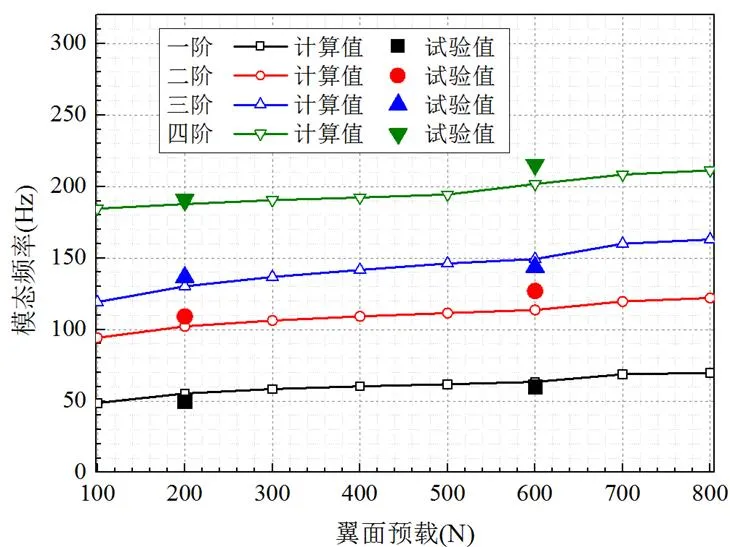
图8 不同载荷条件下的固有频率
4 方法的适用性讨论
本文核心方法是采用局部有限元模型获得一组外载荷与外翼根部响应之间的半解析规律。具体地,采用图3局部模型获得铰接/锁紧结构的运动特性,并放置在bush单元中,而折叠翼整体等效为bush单元效应与翼面弹性变形。一定载荷条件下的含bush单元的模态计算,实际上也是根据特定载荷对应地固化bush单元的刚度值,然后按照固定不变的刚度矩阵[K]进行模态计算。
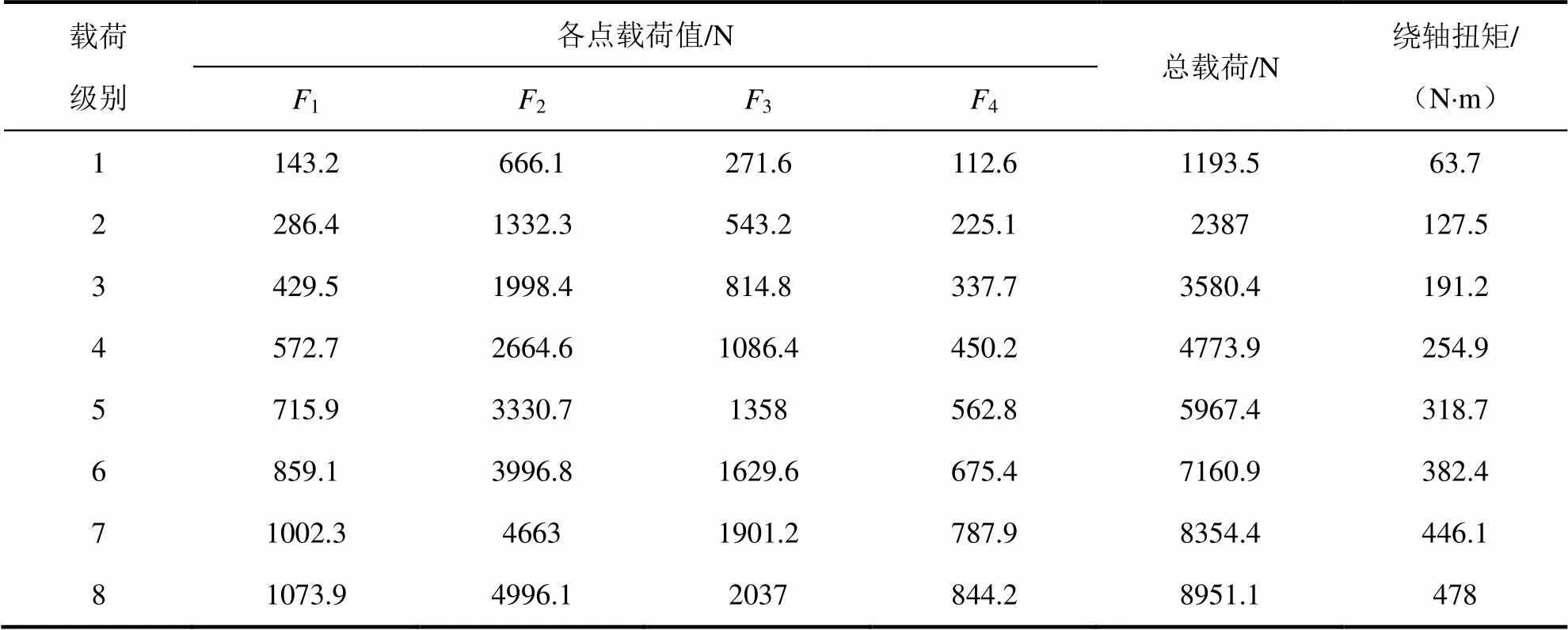
表2 静力试验载荷
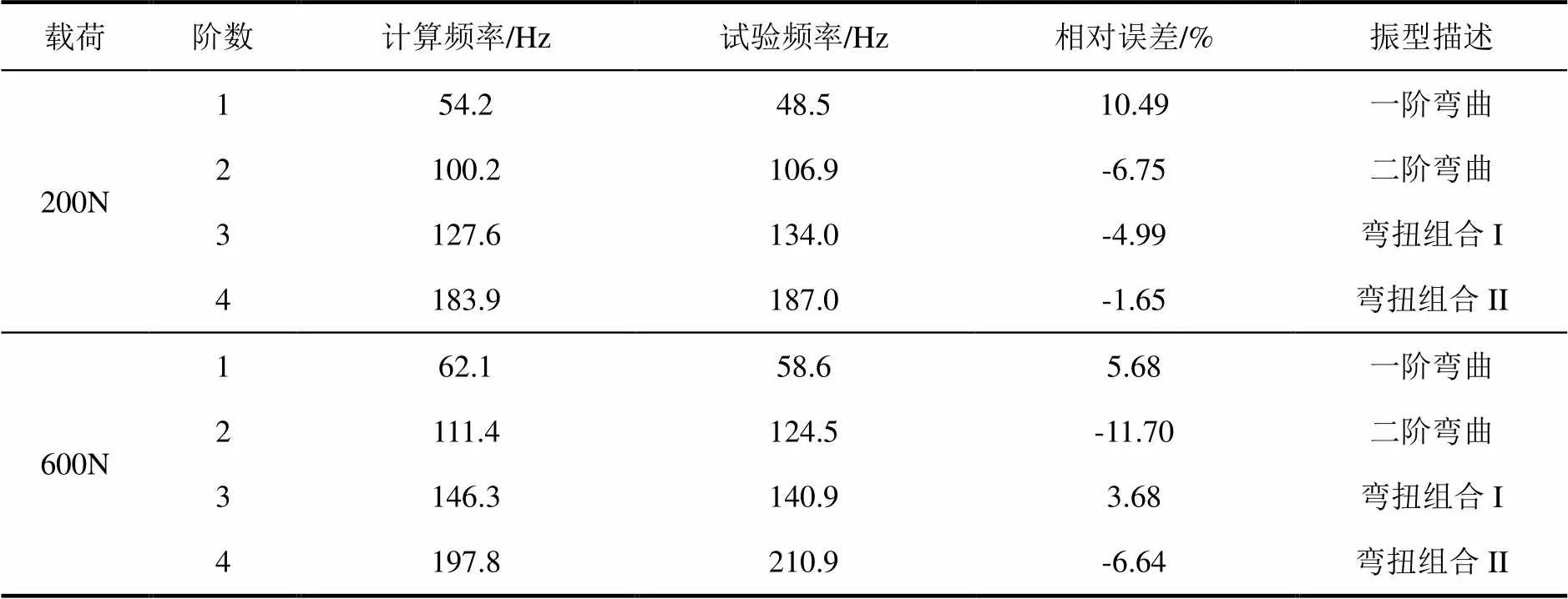
表3 不同负载下模态试验结果
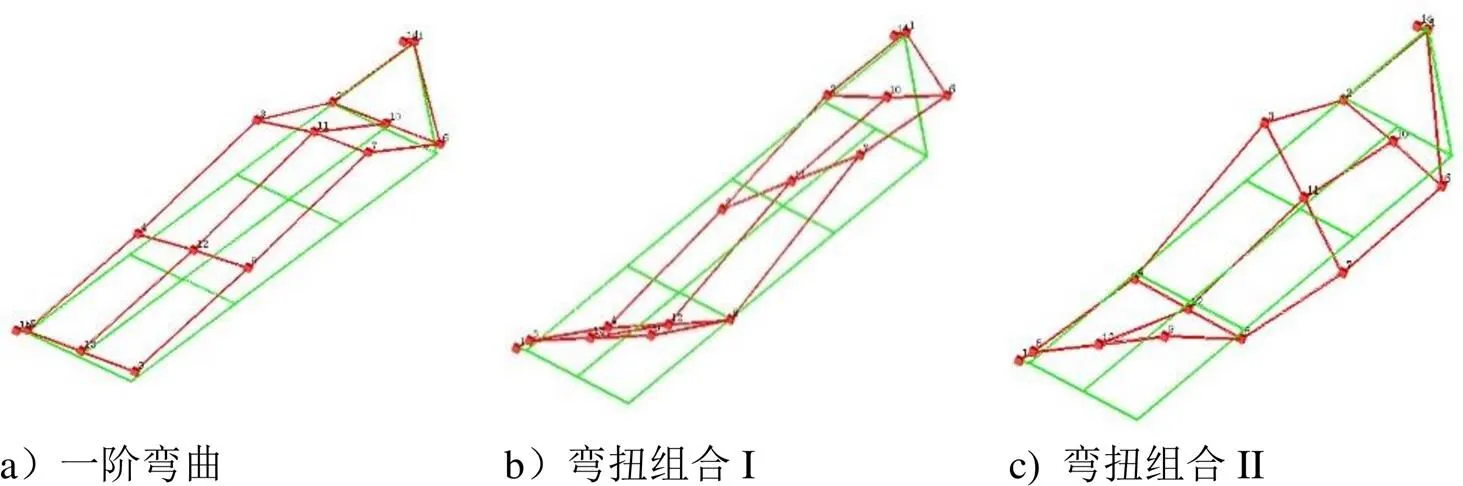
图9 试验振型(二阶弯曲振型试验中未记录)
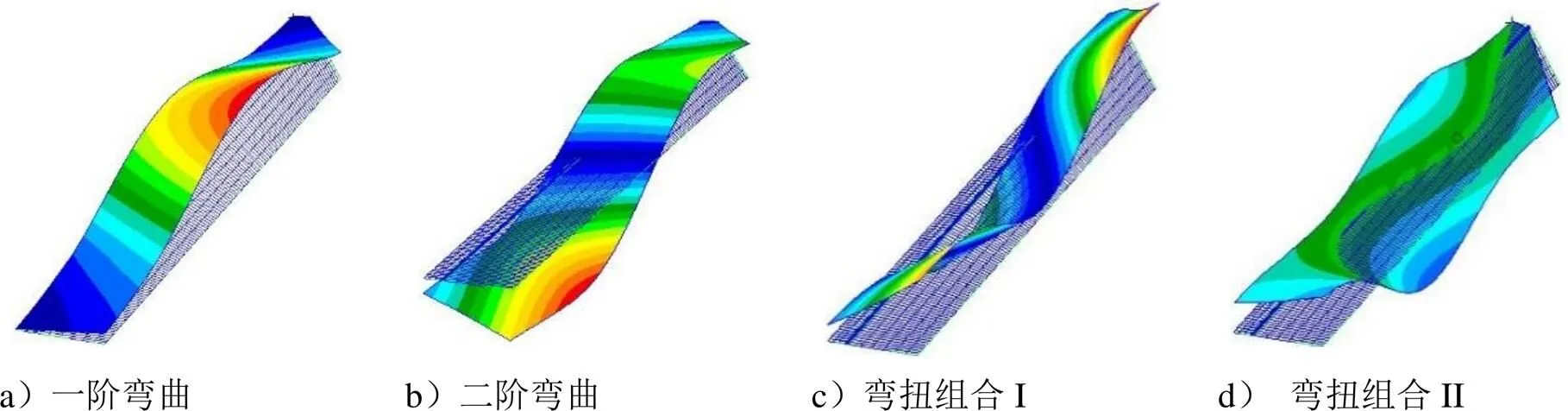
图10 计算振型
商用有限元分析软件(例如Abaqus)无需对模型进行分割和局部求解,针对翼面整体模型按照不同载荷步亦可以进行模态计算:第1步是先对含铰接/锁紧结构接触和间隙特点的翼面整体有限元进行静力计算,获得接触刚度具体情况;第2步模态计算时则固化第1步算得的接触刚度情况,不再考虑接触非线性,进行模态求解。
不妨定义对翼面整体先进行静力分析,再开展含预载模态分析的方法为“整体两步法”;定义本文采用的先开展局部刚度计算,再将简化弹簧带回至整体结构进行分析的方法为“局部弹簧法”。针对两种方法的适定性问题,具体地,局部弹簧法优于整体两步法之处,做以下讨论。
对接触配合结构的分析主要包含三类:静力学分析、模态分析和时域响应分析。
对于含接触问题的非线性静力学分析,采用本文的局部弹簧法意义不明显。该方法可能因为破环原有结构的传力路径,进而导致刚度弱化。局部模型由整体模型切出,局部模型与结构本体之间切割面的应力边界和位移边界难以真实比拟,这势必导致在网格质量相近时局部模型求解的精度难以达到整体三维有限元模型的精度。
对于含接触问题的模态分析,目前整体两步法和局部弹簧法在连接结构模态分析的文献中均有应用,其中局部弹簧主要用于连接刚度的辨识研究。但是整体两步法中如何固化静力分析获得的接触刚度可能仍存一定争议,而局部弹簧法本质上也是固化接触刚度的一种方式。此外,就方法的成熟度而言,整体两步法为新兴方法,但是采用等效弹簧的思想已在航空飞行器的连接边界处理有较为广泛的应用,相比而言成熟度更高。
对于时域响应分析,例如折叠翼面的非线性气弹颤振分析,已有文献近乎一致地采用了局部弹簧法进行建模。这是由于在进行时域响应计算时,若采用整体模型在每一时刻步均需要接触迭代至收敛,求解量之大可能难以承受,需要对局部连接模型进行简化;采用整体模型难以获得局部连接刚度,即无法求得等效弹簧刚度,而要想获得等效弹簧的刚度就必须将局部与整体切离单独分析,本文提出的“bush单元效应+翼面弹性变形”思想,包括与之对应的针对局部铰接/锁紧结构“刚性位移与柔性变形的解耦”、以及采用卡尔丹角对含间隙结构“平动位移与转动位移的解耦”,都是提高局部连接刚度求解精度的有效方法;更进一步地,本文创新性地将文献中普遍采用的“单自由度扭簧”模拟折叠铰接刚度推广至“六自由度弹簧”模拟连接刚度,进而提高模态求解的精度,这些正是本文方法的建立初衷和优势所在。
5 结论
1)本文基于有限元分析给出了铰接锁紧结构的连接刚度计算方法,将外翼面节点位置抽象为折叠轴根部浮动坐标系的宏观平动和转动刚体位移与翼面自身柔性变形叠加,根据平动、转动位移与外载荷的关系来求解连接刚度,该刚度求解方法具有一定的合理性。
2)静力学分析给出了不同工况下锁紧结构的载荷位移曲线,计算结果表明,随载荷值增大,刚度值呈现出“双线性”和“渐刚性”两种特性;对折叠翼面在正向载荷和反向载荷下的研究结果表明连接刚度具有显著的非对称特性。
3)对折叠翼面整体的模态分析表明,采用本文的刚度计算方法获得的翼面振动频率与试验频率的误差小于12%,振型结果与试验结果吻合良好。本文提出的方法对可折叠翼面的锁紧结构优化设计、动力学分析和预示均具有一定的参考性,为后续的翼面热气动弹性分析提供基础。
[1] Wood B, Heinrich B, Sutter G, et al.The development of a simplified fin folding mechanism for a future space transportation vehicle [C].Proceedings of 11the ESMATS Symposium, Switzerland, 21-23 September 2005: 143-152.
[2] Lupo C, Robertson B, Gafka G.The X-38 V201 Fin folding actuation mechanism [R].NASA/CP-2004-212073, 2004.
[3] Shin W H, Lee I, Shin Y S, et al.Nonlinear aeroelastic analysis for a control fin with an actuator [J].Journal of Aircraft, 2007, 44(2): 597-605.
[4] Lee D H, Weisshaar T A.Aeroelastic studies on a folding wing configuration [C].46th AIAA/ASME/ASCE/ AHS/ASC Structures, Structural Dynamics and Materials Conference, (AIAA 2005-1996), 2005:1-13.
[5] Dussart G, Lone M, O’Rourke C, et al.In-flight folding wingtip system: inspiration from the XB-70 Valkyrie[C].AIAA SciTch Forum, 2019: 1-17.
[6] Verstraete M L, Roccia B A, Mook D T, et al.A co-simulation methodology to simulate the nonlinear aeroelastic behavior of a folding-wing concept in different flight configurations [J].Nonlinear Dynamics, 2019, 98(2): 907-927.
[7] Tang D, Dowell E H.Theoretical and experimental aeroelastic study for folding wing structures [J].Journal of Aircraft, 2008, 45(4): 1136-1147.
[8] Snyder M P, Sanders B, Eastep F E, et al.Vibration and flutter characteristics of a folding wing[J].Journal of Aircraft, 2009, 46(3): 791-799.
[9] Castrichini A, Siddaramaiah V H, Calderon D E, et al.Nonlinear folding wing tips for gust loads alleviation [J].Journal of Aircraft, 2016, 53(5): 1391-1399.
[10] 何昊南, 于开平, 唐宏, 等.有间隙折叠舵面的振动实验与非线性建模研究[J].力学学报, 2019, 51(5):1476-1488.[He Haonan, Yu Kaiping, Tang Hong, et al.Vibration experiment and nonlinear modelling research on the folding fin with free-play.Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(5): 1476-1488.]
[11] He HN, Tang H, Yu KP, et al.Nonlinear aeroelastic analysis of the folding fin with free-play under thermal environment [J].Chinese Journal of Aeronautics, 2020, 33(9): 2357-2371.
[12] Hu W, Yang Z C, Gu Y S.Aeroelastic study for folding wing during the morphing process [J].Journal of Sound and Vibration, 2016, 365(17): 216-229.
[13] Hu W, Yang Z C, Gu Y S, et al.The nonlinear aeroelastic characteristics of a folding wing with cubic stiffness [J].Journal of Sound and Vibration, 2017: 22-37.
[14] Wu Z G, Yang N, Yang C.Identification of nonlinear structures by the conditioned reverse path method [J].Journal of Aircraft, 2015, 52(2): 373-386.
[15] Ma Z S, Wang B, Zhang X, et al.Nonlinear system identification of folding fins with free-play using direct parameter estimation [J].International Journal of Aerospace Engineering, 2019, 1-8.
[16] Yang N, Wang N, Zhang X, et al.Nonlinear flutter wind tunnel test and numerical analysis of folding fins with free-play nonlinearities [J].Chinese Journal of Aeronautics, 2016, 29(01): 144-159.
[17] Kennedy J, Eberhart R.Particle swarm optimization [J].IEEE International Conference on Neutral Network, 1995, 4:1942-1948.
A Dynamic Model of Hinged-locking Structures Based on Contact Theory
REN Hao-yuan WANG Yi WANG Liang ZHOU Jian-bo CHANG Han-jiang CAI Yi-peng WANG Le LEI Bao
(China Academy of Launch Vehicle Technology, Beijing, 100076, China)
Based on the displacement vector equation and finite element method, a process to solve the local connection stiffness of hinged-locking structures for folding wing is established, and the numerical simulation and experiments research for the whole wing are also performed.Firstly, the node displacement vector equation is derived, and the influence of flexible deformation of out-wings and clearance between spatial revolute joints is considered.Then, the statics analysis on hinged-locking structures is performed.The nonlinear connection stiffness, applying translation vector and rotation matrix under different loads, is acquired by using particle swarm optimization method.Finally, local stiffness value is applied to the plate-spring model of the overall structure for static and modal analysis.The results show that the simulated value and experimental value are in good agreement, which verifies the accuracy and usability of the stiffness simulation method.The method proposed in this paper provides reference for the optimization design of locking structure and structural dynamics analysis of a folding wing.
Folding wing; Connection stiffness; Static analysis; Modal analysis
V416.2
A
1006-3919(2021)06-0031-08
10.19447/j.cnki.11-1773/v.2021.06.005
2021-05-28;
2021-10-26
国家自然科学基金项目(11902363)资助
任浩源(1994—),男,博士生,研究方向:航空宇航科学与技术;(100076)北京9200信箱1-1分箱.

