基于局域压缩量子剪切制备非高斯量子态及非经典性

余 敏,叶 炜,常守康,夏 莹,张 欢,胡利云

(1.江西师范大学 量子科学与技术中心，江西 南昌 330022；2.江西师范大学 物理与通信电子学院， 江西 南昌 330022；3.中南大学 计算机学院，湖南 长沙 410083；4.中山大学 物理学院，广东 广州 510275)

0 引言

量子信息技术的蓬勃发展使得人们对信息传递的效率和测量精度的要求越来越高，而以经典光场为信息载体已经远远满足不了科学发展的需求[1-6]。例如，在量子度量领域，当非经典量子态作为干涉仪的输入态时，标准量子极限可以被突破，这是输入经典态所不能及的[5-7]。因此，如何制备和调控强非经典性的量子态成为了顺利完成量子信息任务的前提。

在连续变量范畴里，量子态可被分为高斯态和非高斯态，这两种态最为明显的区别在于其相应Wigner函数的表现形式[8-10]。此外，不同于后者，前者亦可通过当前的实验技术比较容易地被实现[11，12]。不幸的是，高斯态在完成某些特定的量子信息任务存在一定的局限性。例如，双模压缩真空态虽然在高精密相位灵敏度接近海森堡极限，但是压缩参数实际上被限制在1.15内[13，14]。为此，人们把研究目光聚焦在非高斯量子态上。一般而言，非高斯量子态的制备通常都要利用到非高斯操作，比如，光子扣除[3，4,15],光子增加[16,17]和这两者的相干叠加操作[18，19]。尤其是，光子增加和光子扣除操作已经被实验上用来证明量子力学算符的不对易性[20]。此外，这两种操作不仅可以被用来实现量子态非经典性的增强，还能进一步改善高斯态(如双模压缩真空态)的纠缠度。具体而言，在1991年，AGARWAL G S等提出了一种利用光子增加操作将经典的相干态转变为高非经典的量子态，并利用准概率分布函数讨论了非经典性的强弱[21]。在2014年，KUROCHKIN Y 等在实验上证明了光子扣除操作可以使得双模压缩真空态的纠缠度和压缩度提高50%左右[22]。另一方面，NHA H 等提出了利用光子增加和扣除的相干叠加操作将经典光场转变为非经典光场[23]。基于这种叠加操作的特性，Zhang等人还利用了粒子守恒叠加操作提高了双模压缩真空态的纠缠度以及量子隐形传输的保真度[24]。除了上述常见的非高斯操作之外，量子催化操作首次被LVOVSKY A L等人提出[25]，在量子态工程上具有潜在的应用前景。在量子催化过程，虽说这种操作看似没有在光路上增加或者扣除光子，但是将输入的相干态转变为具有高非经典的量子态[25]。自此，量子催化操作在提升量子纠缠[26]，量子相干[27]和量子密钥分发性能方面[28，29]扮演着重要的角色。

作为另一种可实现非高斯态制备的方案，在1998年，PEGG等人提出了一种可以将相干态截断为真空态和单光子态叠加的量子剪切[30]。此后，量子剪切被用来实现无噪声放大[8,30]，这种放大器在提升量子密钥分发的通信距离上也被广泛地研究[31-33]。在2019年，这种剪切装置被Hu等人作用到双模压缩真空态中，并考虑了开放系统下的剪切效果[34]。研究结果表明，即使是在有耗散的情况下，这种剪切装置仍然可以提高双模压缩真空态的纠缠度，而且这种提升效果比量子催化的情况更为显著。最引人注目的是，局域压缩操作嵌入到量子剪切里可以进一步地放大增益因子[35]，但并未讨论此方案下量子态的非经典特性。因此，基于上述背景，本文将局域压缩操作引入到量子剪切装置中，并以相干态作为输入态时，着重研究输出态的量子统计特性，主要涉及平均光子数和Wigner函数。特别要指出的是，本方案基于两个单光子输入和单光子探测，实现了真空态，单光子态与双光子态的叠加，与实现真空态、单光子态叠加的方案不同[35]。研究表明，在相同参数下，局域压缩度的增加有助于平均光子数的提高以及Wigner函数负部体积的增大，这意味着这种局域压缩操作在量子度量等领域具有潜在的应用。

本文结构安排如下：第2节首先简要介绍了局域压缩的量子剪切装置结构。然后，从输入输出关系出发，获取局域压缩的量子剪切装置的等效算符。当考虑了相干态作为输入态时，第3节利用了平均光子数和Wigner函数来讨论输出态的非经典性。最后，第4节对本文进行总结。

1 基于局域压缩的量子剪切装置和非高斯态的制备

本节首先简要介绍局域压缩的催化式量子剪切装置，重点推导出这种装置的等效算符，从而建立起量子态输入-输出关系。然后，假定输入态为相干态时，本节可进一步获取非高斯态的具体表达形式，继而考察所制备出非高斯态的成功概率。

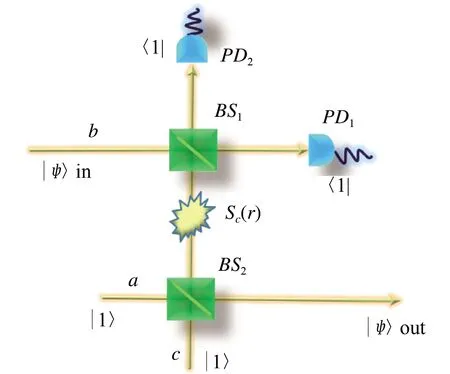
图1 基于局域压缩的催化式量子剪切装置

1.1 局域压缩的量子剪切装置及其等效算符

如图1所示，局域压缩的催化式量子剪切装置有三个输入端口(分别标记为a,b,c模)，其中，a,c模的输入端口有单光子输入，b,c模的输出端口分别做单光子探测。这类似于单光子催化操作，因为在量子催化过程中，辅助模的输入-输出Fock态似乎保持不变，但对主模之间的量子态转换起到一定的作用.在该装置中，两个光分束器(分别标记为BS1和BS2)对a,c模和b,c模光具有合束与分束的作用效果。在算符形式上，这两个分束器可以分别表示为BS2=eθ2(ac+-a+c)和BS1=eθ2(bc+-b+c)，其中BSj的透射率为Tj=cos2θj,(j=1,2)。为了在c模上引入局域压缩操作Sc(ξ)=exp[ξ(c2-c+2)/2](ξ为压缩参数)，这里假设将局域压缩放置在两个光分束器之间。于是，整个局域压缩的催化式量子剪切装置则可被看作一种等效算符，即

O=c1|b1|BS1Sc(r)BS2|1a|1c，

(1)

为了获得上述等效算符的解析表达式，这里须采用算符的变换关系：

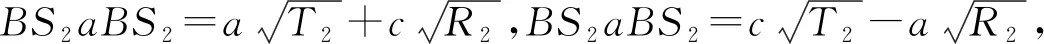
(2)

式中Rj=1-Tj,(j=1,2)为反射率。因此，结合式(1)和式(2)，局域压缩的催化式量子剪切装置的等效算符可进一步表示为

(3)

其中

(4)

由式(3)可知，整个装置的作用效果就是真空态，单光子态，双光子态投影算符的叠加。这意味着，对于任意的输入态(见图1)，经过此装置后，输出态可被截断为真空态，单光子态和双光子态的叠加形式。此外，不同于文献[32]的工作，局域压缩操作的引入导致了等效算符中增加了w3|0>ab<2|和w3|2>ab<0|两项，这或许在量子态非经典性的改善方面起到显著的效果。特别地，当压缩参数ξ=0时，式(4)可简化成

(5)

这与文献[32]的结果一致。

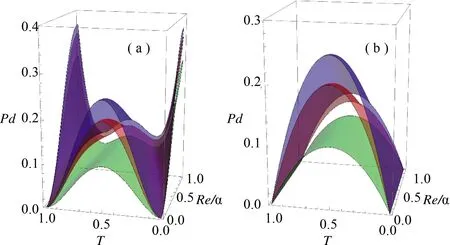
图2 (a) 对于透射率T1=T2=T，(b) 透射率T1=T,T2=0.5，成功概率Pd在(T,Re[α])空间的分布，其中ξ=0(上面)，ξ=0.2(下面)，ξ=0.4(下面)

1.2 非高斯态的制备及其成功概率

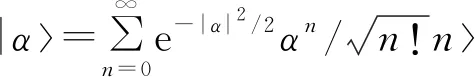
由图1可知，对于任意输入态|ψin，则经过局域压缩的催化式量子剪切装置后的输出态可以表示为

(6)

这里Pd表示所制备非高斯态的归一化系数(或者成功概率)

(7)

利用量子态的正交归一性，它的解析表达式具有如下形式

Pd=e-|α|2(|c0|2+|c1|2+|c2|2)。

(8)

根据式(8)，不同压缩参数ξ=0,0.2,0.4下，图2绘制出了，成功概率Pd随透射率T和相干态振幅Re[α]的变化曲面。显然，在相同参数条件下，随着局域压缩参数的增加，成功概率Pd也在逐渐降低，这一定程度上反映出实际调控局域压缩的困难。尽管如此， 局域压缩操作的引入却可以有效地放大增益因子，这在量子信息处理上有着潜在的应用。此外，当取相同的压缩参数和振幅时，相比于T1=T,T2=0.5的情况，见图2(b)，对于T1=T2=T的成功概率除了T=0.5外还在T→0或者1达到了最高值，见图2(a)。这说明T1=T2=T的情形下的成功概率要优于T1=T,T2=0.5的情况。从图2(a)还可知，当取相同的压缩参数时，T→0或者1的成功概率可以随着振幅的增加而增加，这是完全不同于T1=T,T2=0.5的情况.由此可见，输入相干态的振幅在某种特殊情况下有利于增加非高斯态的实现几率。

2 非高斯量子态的非经典特性

在讨论完非高斯态的成功概率后，本节从平均光子数和Wigner函数的负部特征方面来考察输出态的统计特性，重点分析域压缩操作对输出态统计特性的影响。

2.1 平均光子数

平均光子数作为光场量子态统计的特征之一，尤其在量子度量领域扮演着重要角色。例如，在光学干涉仪系统中，平均光子数越高则会使得量子费舍信息越大，从而达到更高的相位灵敏度[33]。那么，在本文所提方案中，局域压缩的引入能否进一步的提高输出态的平均光子数呢？本节对输出态的平均光子数进行研究。

如图1所示，对于a模输出的任意量子态ρout，它的平均光子数都可以被定义为

(9)

结合式(6)和式(9)，输出态的平均光子数的解析表达式为

(10)

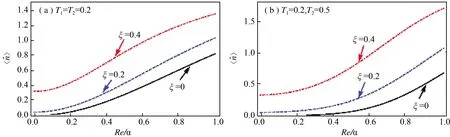
图3 (a) 对于透射率T1=T2=0.2，(b) 透射率T1=0.2,T2=0.5，平均光子数随Re[α]的变化，其中ξ=0(实线)，ξ=0.2(虚线)，ξ=0.4(点划线)

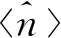
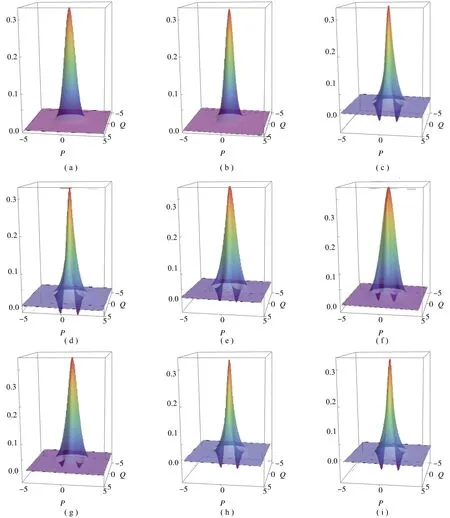
图4 对于不同的相干态振幅，局域压缩参数和光分束器的透射率(这里我们设T1=T2=T)，输出态的Wigner函数W(β)在相空间(Q,P)中的分布；(a)-(c)：给定输入相干振幅Re[α]=0.1和透射率T=0.2,分别对应ξ=0,0.2,0.4；(d)-(f):给定ξ=0.4和T=0.2，分别对应Re[α]=0.1,0.3,0.5；(g)-(i)：给定Re[α]=0.1和ξ=0.4，分别对应T=0.1,0.3,0.5

2.2 Wigner函数

Wigner函数是一种典型的准概率分布函数，原因在于它的值不仅仅局限于(0.1/π)，其在相空间分布中常常会出现负值区域。一般而言，这种负值区域越大表明量子态的非经典性越强，因此Wigner 函数也通常被用来判断光场态的非经典性强弱[34]。基于此背景下，本小节利用关于Wigner函数的积分公式量化负部体积的大小，以便于直观地看出Wigner函数负部体积随局域压缩参数、输入相干态振幅的变化。这里，首先给出Wigner函数在相干态表象下的表达形式，即

(11)

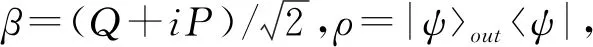
(12)

为了更加清晰地展示出输出态的非经典特性，根据式(12)，对于不同参数(包含了局域压缩ξ，振幅Re[α]和光分束器的透射率T)，图4给出了Wigner函数在相空间(Q,P)中的分布曲面。为了便于分析和讨论，这里仅考虑两个分束器的透射率相同的情况，即T1=T2=T。由图4可知，对于给定的透射率T=0.2和相干态振幅Re[α]=0.1时，Wigner函数的负部体积随着局域压缩参数的增大而增大(见图4(a)-(c))。但是，对于给定的透射率T=0.2和局域压缩参数ξ=0.4时，随着振幅的增加，Wigner的负部体积却是减小的(见图4(d)-(f))。 这些研究结果表明，局域压缩的增大利于增强输出态的非经典特性，而输入相干态的振幅越小对非经典性的增强越有益。值得一提的是，从图4(g)-(i)中，对于给定的相干态振幅Re[α]=0.1和局域压缩参数ξ=0.4，透射率T的增加t=0.1,0.3，相应的Wigner函数的负部体积在增大；而透射率T从0.3到0.5的变化对负部体积影响甚微。于是，为了进一步看清非经典性的强弱变化，这里将利用Wigner函数的负部体积表达式来进行量化，它可以被定义为

同样地，在与图4相同的参数取值下，根据式(13)，表1给出了相应的输出态Wigner函数的负部体积值。除了上述研究结果外，由表1的第1-3行可知，对于ξ=0的情况，Wigner 函数的负部体积还是存在的，这表明利用量子剪切装置确实可以把经典态转换为非经典态[26]。此外，由表1的第7-9行可知，随着透射率T的增加(T局限在(0,0.5]内)，V(β)是逐渐地增加。在相同参数下，由于Wigner函数的负部体积关于T=0.5对称，因此这里不再考虑T∈[0.5,1)的情形。

(13)

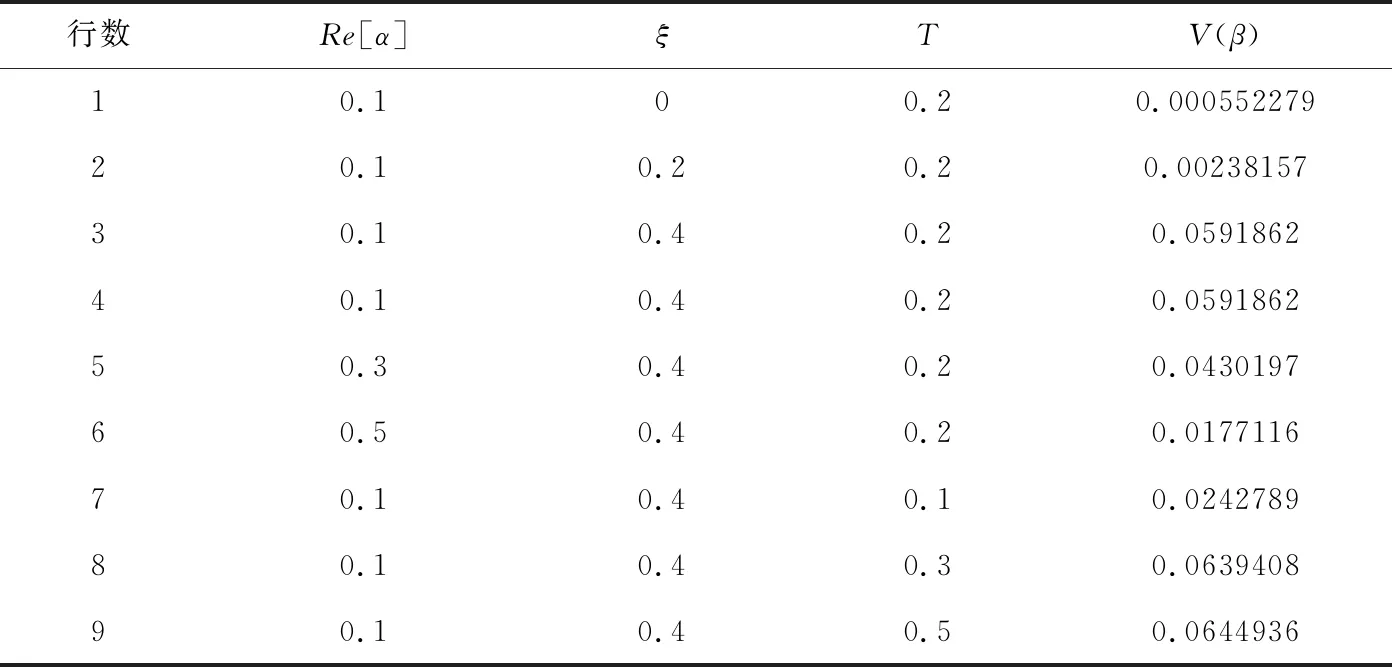
表1 Wigner函数的负部体积，其中第1-3行为给定Re[α]=0.1和T=0.2,负部体积值随ξ的变化；第4-6行为给定ξ=0.4和T=0.2，负部体积值随Re[α]的变化；第7-9行为给定Re[α]=0和ξ=0.4，负部体积值随T的变化

3 结论

当考虑输入相干态时，本文主要利用局域压缩的量子剪切来制备非经典态，并考察了输出态的量子非经典特性。从输入输出关系出发，本文首先获得基于局域压缩量子剪切的等效算符，它可以将经典的相干态截断为真空态，单光子态和双光子态的叠加形式。此外，以输入相干态为例，本文导出输出态的解析表达式及其实现的成功概率。研究发现，对于给定的相干态振幅和光分束器的透射率，随着嵌入的局域压缩参数的增加，成功概率有所降低。尽管如此，在相同参数下，局域压缩对输出态的量子非经典特性却是有益的。具体而言，平均光子数随着嵌入的局域压缩参数或输入相干态的振幅的增大而增加，这为在量子度量学中研究量子费舍信息提供了一个重要的途径。类似地，Wigner函数的负部体积随着局域压缩参数增加而增大，从而表明了基于局域压缩的量子剪切装置可以进一步增强输出态的非经典性，这些研究结果有望为量子度量中相位精度的提升做了有效的贡献。