两种典型立柱截面浮式平台涡激运动耦合特征试验研究

魏东泽，阙小玲，杨晨斌，白兴兰

（浙江海洋大学a.海洋工程装备学院；b.船舶与海运学院，浙江舟山316022）

0 引 言

浮式平台的涡激运动会加重立管、锚泊系统的疲劳损伤，降低使用寿命，因此一经发现就成为了海洋工程界的研究热点之一。目前深水海洋平台，如半潜式平台及TLP平台，其立柱截面形状主要以圆形和方形为主，国内外已有诸多学者[1-6]针对不同立柱截面形状的海洋结构物VIM问题进行了研究，但大多将研究重点集中在横荡及纵荡两个自由度上。随着研究的深入，学者们发现在一定的来流条件下平台会发生较为剧烈的艏摇运动：Goncalves 等[7-9]针对带圆形倒角的方形立柱半潜式平台的VIM问题进行了一系列的试验研究，探讨了各个流向下艏摇运动的响应幅值与约化速度的关系，并指出在进行半潜式平台设计时不应忽略艏摇运动的影响；Liu[10]等采用模型试验的方法对方形立柱半潜式平台的涡激运动问题进行了研究，以艏摇运动为重点探讨来流方向和纵横比对平台VIM特征的影响，从各个流向下横荡运动以及0°流向下艏摇运动观察到了“涡激共振”现象；Gu[11]等对深吃水变截面立柱的新型FDPSO 进行了数值模拟研究，分析了其横荡、纵荡及艏摇运动情况，并将模型试验结果与数值模拟结果进行了对比验证，结果表明，新型FDPSO 的涡激运动特征与传统FPSO 有所不同，45°流向下艏摇运动响应幅值远大于0°流向情况，并且艏摇运动频率主峰值接近平台固有频率；Kim[12]等采用DDES-SST 模型对八立柱结构型式的半潜式平台VIM 问题进行了数值模拟研究，并将所得结果与模型试验结果进行了对比，发现在横荡、纵荡及艏摇的响应频率和响应幅值方面均拟合良好，其研究结果为半潜式平台的VIM预测提供了一种实用方法。

目前学者们对于浮式平台艏摇问题的研究主要集中于流向角、纵横比等因素对于艏摇运动响应幅值的影响。本文对两种典型立柱截面的海洋浮式平台在不同流向下的涡激运动问题进行了试验研究，并以艏摇运动为重点，分析来流方向和立柱截面形状对平台三自由度运动响应幅值的影响，并探讨了在涡激运动的不同阶段中，艏摇运动与横荡、纵荡运动的耦合关系。

1 模型试验方案

1.1 模型介绍与试验方案

本试验模型为典型四立柱结构，由有机玻璃制成，平台立柱有圆柱和方柱两种，圆柱平台（circu⁃lar cross-section platform ，简写为CCP）和方柱平台（square cross-section platform，简写为SCP）几何尺寸如表1 所示。试验水槽长30 m、宽1 m、深1 m，水槽边壁距离两平台立柱外缘分别为40 cm 和38 cm，均大于6 倍立柱特征长度，因此边壁效应基本可以忽略。试验采用循环式潜水泵造流系统造流，最大造流能力可达0.8 m/s。本试验设计了一种由四组弹性系泊缆组成的等效系泊方案，分别将模型底部、模型上部与固定用铁环相连，以模拟平台在真实工作环境下的水平、垂直系缆刚度。在前后立柱中上部及平台底部质心处分别安装加速度传感器，采用DASP多功能数据采集分析系统对加速度信号进行采集，通过对加速度数据进行二次积分处理获得平台横荡、纵荡及艏摇响应时程曲线。试验装置如图1所示。

表1 两平台模型参数Tab.1 Main parameters of the platforms

图1 平台模型Fig.1 Platform models

1.2 自由衰减试验

为了获取平台各自由度的固有频率，首先进行了自由衰减试验。试验流速范围为0.06～0.50 m/s，共16 个流速工况。通常情况下，海洋工程结构锁定现象发生的约化速度范围约为4～11，16 个试验工况对应约化速度应尽量大于此范围。通过调整系缆刚度可以改变系统固有频率，从而达到使约化速度范围满足试验需要的目的。对横荡、纵荡及艏摇自由衰减时程曲线进行傅里叶变换，所得结果如图2 所示，可得fc-sway=fc-surge=0.67 Hz、fc-yaw=1.58 Hz，fs-sway=fs-surge=0.54 Hz、fs-yaw=1.28 Hz，其中，下标c 表示圆柱平台，下标s 表示方柱平台。可以计算出对应的约化速度范围分别为：圆柱1.79～14.93、方柱1.85～15.43，包括了通常情况下的锁定区及锁定区前、后足够宽阔的约化速度范围，使试验结果能更好地反映平台运动的运动规律。

图2 两平台自由衰减FFT曲线Fig.2 Free attenuation curve after the Fourier transform of two platforms

采用约化速度反映流速对平台涡激运动特征的影响，约化速度表达式如下：

为分析艏摇固有频率对平台涡激运动特征的影响，定义Ury为采用艏摇固有频率表达的约化速度，即

计算得对应的Ury范围为：圆柱0.76～6.33，方柱0.78～6.51。式中，U为试验流速，D为特征长度。

2 试验结果与数据分析

2.1 运动响应幅值分析

图3 给出了圆柱和方柱平台在来流方向分别为0°和45°时横荡运动响应幅值随约化速度变化情况。由图可见，两流向下的圆柱平台以及45°流向下方柱平台的横荡运动在约化速度约为5～12 的范围内都发生了较为明显的“涡激共振”现象，而0°流向下方柱平台的横荡运动响应幅值则始终保持随约化速度的增大而增大的趋势。在绝大多数工况下，圆柱平台的横荡运动幅值均明显大于方柱平台，两者相差最大可达6.1倍，但是在流向角为45°时，圆柱和方柱的横荡运动幅值比较接近，当约化速度超过12后，方柱平台的横荡运动幅值甚至超过了圆柱平台。

图4给出了圆柱和方柱平台在来流方向分别为0°和45°时纵荡运动响应随约化速度的变化情况。由图可见，圆柱平台的纵荡运动在约化速度大约4～8范围内发生了小幅的“涡激共振”现象，但幅值增大并不明显。总的来说，两流向下，两平台的纵荡运动响应幅值基本保持随约化速度增大而增大的趋势。相同流向下，在整个约化速度范围内，两平台纵荡运动幅值较为接近，但前者始终稍大于后者，其中圆柱平台纵荡运动最大幅值为0.33D，方柱平台为0.24D。

图3 不同流向下两平台横荡响应幅值Fig. 3 Transverse responsive amplitude of two platforms at different current headings

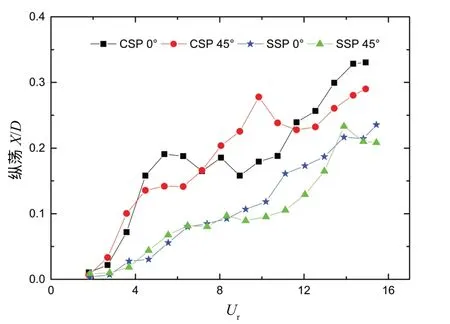
图4 不同流向下两平台纵荡响应幅值Fig.4 Inline responsive amplitude of two platforms at different current headings

图5 给出了圆柱和方柱平台在来流方向分别为0°和45°时艏摇运动响应随约化速度的变化情况以及与Goncalves 经典试验所得结果的对比情况,图中底部横坐标为约化速度Ur，顶部横坐标为采用艏摇固有频率表示的约化速度Ury。由图可见，本试验所得圆柱平台的艏摇运动响应幅值大小以及随约化速度变化规律与Goncalves试验结果十分接近，说明了本文模型及试验方案的可靠性。此外，本文所得艏摇响应幅值与Goncalves 经典试验结果也有一些不同之处。首先，在Goncalves 试验中，各个流向下的艏摇运动响应幅值在通常情况下锁定区范围内（约化速度约为4～10）均没有观察到“涡激共振”现象，而在0°流向下，Ury在4～8范围内，平台艏摇运动发生了明显的涡激共振现象，体现了艏摇固有频率对平台涡激运动特征的影响。本试验中，在45°流向下，约化速度约为4～11 范围内，从方柱平台的艏摇运动观察到了明显的涡激共振现象，这说明在特定流向下艏摇运动也可能发生涡激共振。因此，在进行平台、立管等结构的设计时，应考虑大幅艏摇运动问题。当Ury≥4 时，圆柱平台、方柱平台的艏摇运动响应幅值出现了大幅增大的现象，究其原因，应为此时艏摇运动频率（fc-yaw≥1.24 Hz，fs-yaw≥0.93 Hz）分别与各自艏摇固有频率接近，而使艏摇运动发生共振现象，同样体现了艏摇固有频率对平台VIM特征的影响。其次，相同工况下本试验中方柱平台获得的艏摇运动响应幅值远大于Goncalves 试验结果，本试验中45°流向下共振区的方柱艏摇运动最大幅值可达20°左右，而Goncalves 试验中，两流向下平台最大艏摇响应幅值仅为5°左右。造成这一差异的原因可能是平台模型的立柱截面形状不同：Goncalves试验采用模型的立柱截面形状为带圆形倒角的正方形，而本试验方柱平台模型截面形状为正方形，没有倒角，涡街脱落形态、分离点位置都有所不同；另外，两试验模型浮箱结构型式以及浮箱高度与平台吃水的比值有所不同，也可能对平台的艏摇运动产生了一定影响。

2.2 三自由度运动耦合特征分析

图6给出了0°流向下，圆柱和方柱平台的横荡、纵荡和艏摇三自由度运动响应频率主峰值随约化速度的变化情况。由图可见，两平台三自由度运动频率主峰值随约化速度变化规律比较类似，大致都可以分为3个阶段。第一阶段中，涡激运动尚未发生，此时平台各自由度运动的主峰频率值基本耦合于平台的固有频率。第二阶段包括了涡激运动的非锁定区及锁定区，在这个阶段中，两平台的三自由度响应频率具有相似的耦合关系：横荡、纵荡及艏摇响应频率主峰值基本保持1∶1∶1 关系，说明此时三自由度运动耦合程度较高。两平台的横荡响应均只有唯一峰值频率，两平台的艏摇响应频率均出现了与主峰频率成2倍、3倍关系的次峰频率，如图7（a）、（b）所示；圆柱平台的纵荡响应由于受到艏摇运动影响，出现了次峰频率，并且耦合于艏摇运动的2倍关系峰值频率，如图7（a）所示；方柱平台的纵荡响应只有唯一峰值频率，如图7（b）所示。第三阶段为涡激运动的超锁定区阶段。在这个阶段中，平台三自由度运动的耦合关系比较复杂：圆柱平台的横荡、艏摇运动响应频率主峰值随约化速度的增加进一步增大，并基本保持1∶1.5 关系，如图8（a）所示，方柱平台的横荡、艏摇响应频率主峰值同样随约化速度的增加进一步增大并继续保持1∶1关系，如图8（b）所示。两平台纵荡频率均出现降低，并基本稳定于0.38 Hz 附近，不再随约化速度的增加发生明显变化，结合2.1 节对于响应幅值的分析可以推定，此约化速度范围内两平台的纵荡运动发生了高幅值、低频率的“驰振”现象。另外，圆柱平台的纵荡运动出现了耦合于艏摇运动主峰频率的次峰频率值，说明两者具有较强的耦合关系。

图6 0°流向下两平台运动频率Fig.6 Motion frequencies of two platforms at 0°incidence

图7 0°流向下第二阶段两平台涡激运动频率耦合关系Fig.7 Frequency coupling feature of VIM of two platforms in the second stage at 0°incidence

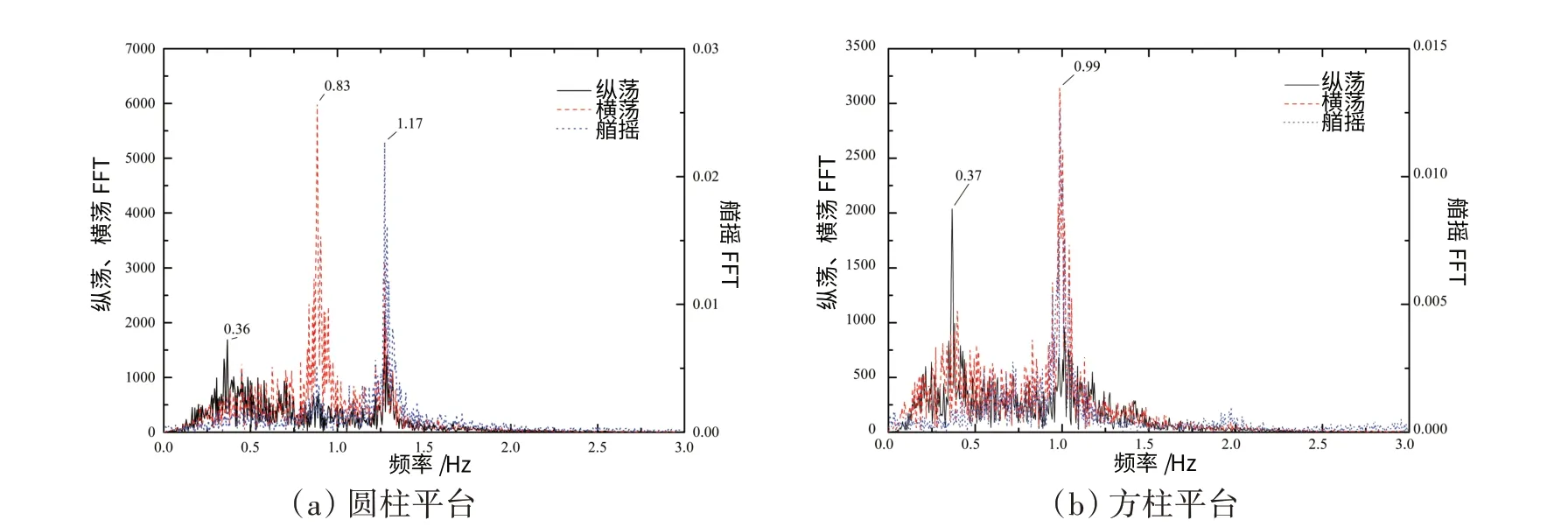
图8 0°流向时第三阶段中两平台涡激运动频率耦合关系Fig.8 Frequency coupling feature of VIM of two platforms in the third stage at 0°incidence

图9给出了45°流向下，圆柱和方柱平台的三自由度运动频率主峰值随约化速度的变化情况。由图可见，两平台三自由度运动频率主峰值随约化速度变化大致也可以分为3个阶段。第一阶段中，两平台三自由度运动频率基本耦合于平台固有频率，而第二、第三阶段中，两平台三自由度运动耦合关系差别较大。第二阶段中，圆柱平台三向运动耦合关系与0°流向第二阶段基本相同，此处不再赘述。第二阶段方柱平台的艏摇运动观察到了特殊的“主频跳动”现象：在此阶段中艏摇运动出现两个明显的峰值频率，数值上与横荡运动频率成1倍和2倍关系，不同约化速度下，这两个峰值频率交替成为艏摇运动的主峰值。例如，当约化速度为4.63 时，艏摇运动频率主峰值为0.46 Hz，与横荡运动频率成1∶1 关系，2 倍频峰值0.92 Hz 为其次峰值，如图10（a）所示；而当约化速度为5.56 时，艏摇运动响应频率主峰值为0.97 Hz，与横荡响应频率成2∶1关系，而1倍频峰值0.49 Hz为其次峰值，如图10（b）所示。此现象说明当流向角为45°时，边界层的涡旋脱落方向具有一定的随机性，导致锁定区域内平台的艏摇与横荡运动频率比例关系具有一定的不确定性。

图9 45°流向下两平台运动频率Fig.9 Motion frequencies of two platforms at 45°incidence

图10 45°流向下方柱平台第二阶段涡激运动频率耦合关系Fig.10 Frequency coupling feature of VIM of SCP in the second stage at 45°incidence

第三阶段中，圆柱平台横荡的运动频率随约化速度的增加逐渐增大，纵荡和艏摇运动在进入第三阶段后频率主峰值出现突增并始终保持基本相同，说明在此阶段纵荡运动与艏摇运动具有较高的耦合性。整个第三阶段中横荡、纵荡、艏摇基本保持1∶1.5∶1.5 的关系，如图11 所示。方柱平台在第三阶段中三自由度运动耦合关系与0°流向时基本相同，纵荡运动也观察到了“驰振”现象。

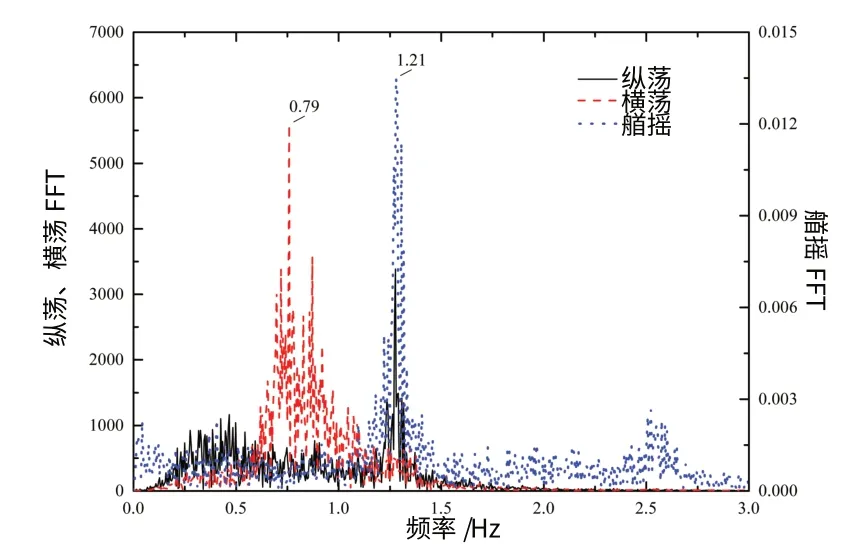
图11 45°流向时第三阶段圆柱平台涡激运动频率耦合关系Fig.11 Frequency coupling feature of VIM of CCP in the third stage at 45°incidence

3 结 论

本文针对两种典型立柱截面形状的浮式平台在不同来流方向下的涡激运动问题进行了试验研究，以艏摇运动为重点，探讨了平台VIM 响应幅值随约化速度的变化情况，以及涡激运动的不同阶段内平台三自由度运动耦合关系，得到以下结论：

（1）圆柱平台在不同流向下的横荡运动均观察到明显的“涡激共振”现象，方柱平台的横荡运动是否发生共振还与来流方向有关。大多数工况下，圆柱平台的横荡响应幅值明显大于方柱平台，两者最大相差6.1倍。

（2）圆柱平台的艏摇运动响应幅值随约化速度变化情况与Goncalves 经典试验结果基本一致。45°流向下方柱平台艏摇运动在约化速度为4～11 的范围内发生了明显的“涡激共振”现象，这与Gon⁃calves 试验结果有明显的不同，说明在一定条件下，艏摇运动发生共振现象的可能性不应该被忽略。在Ury≥4 时，由于艏摇运动频率与艏摇固有频率接近，同样可能引起艏摇运动发生涡激共振现象。另外，相同工况下，本试验中方柱平台艏摇运动响应幅值远大于Goncalves 试验结果，可能与倒角的抑振作用、浮箱结构以及平台吃水等因素有关。

（3）立柱截面形状和来流方向会对浮式平台的涡激运动响应和耦合特征产生明显影响，但呈现出一些基本规律。0°和45°流向下，整个约化速度范围内圆柱和方柱平台三自由度运动耦合关系大致都可以分为3 个阶段：第一阶段中平台三自由度运动频率基本耦合于平台固有频率；第二阶段中，平台三自由度运动频率主峰值基本保持1∶1∶1关系，说明此阶段中平台VIM 具有较高的耦合性；第三阶段中，两平台的运动耦合关系较为复杂，两流向下方柱平台的纵荡运动均观察到“驰振”现象，横荡与艏摇运动频率主峰值基本保持1∶1 关系；0°流向下的圆柱平台纵荡运动也观察到了“驰振”现象，横荡与艏摇运动频率主峰值变为1∶1.5关系，45°流向下圆柱平台的横荡、纵荡及艏摇运动频率主峰值比例关系为1∶1.5∶1.5，这说明在VIM 的超锁定区，方柱平台的艏摇运动与横荡保持较高的耦合性，而圆柱平台的艏摇运动与纵荡运动的耦合性更高，也说明“驰振”现象是否发生与立柱截面形状、来流方向等因素关系密切。