基于半解析法的功能梯度圆锥板自由振动特性

田宏业，刘 朋，胡志宽，邱立凡，陶 沙

（中国船舶科学研究中心，江苏无锡214082）

0 引 言

复合材料结构由于其轻质高强、隐身性能好、耐腐蚀等优点在船舶与海洋工程领域的应用越来越广泛，且在工程应用中遵循着从次承力结构到主承力结构的规律。这就势必导致复合材料结构工作在非常复杂甚至极端的动态环境中，承受着不同性质的动态载荷，并可能导致复合材料结构产生有害振动，引起结构疲劳破坏，对结构的稳定性和系统的安全性构成极大的威胁。因此，开展复合材料结构振动特性规律研究，及时发现复合材料结构振动薄弱环节，对指导复合材料结构工程应用具有重要的意义。

在此研究方面，刘明[1]采用高阶夹层板理论研究了多种新型功能梯度材料软夹芯夹层板壳的自由振动；张玲[2]研究了四边简支边界条件下功能梯度矩形板自由振动特性；牛燕[3]考虑热环境的作用，运用一阶剪切变形理论和von-Karman 型应变位移关系，通过Hamilton 原理推导出功能梯度圆锥曲板的非线性动力学偏微分方程；Abdelkader等人[4]基于四变量板理论对任意梯度的功能梯度板进行了自由振动分析；Jooybar[5]研究了碳纳米管（CNT）功能梯度材料板壳在厚度方向上的分布、几何参数、边缘约束的弹性系数、温度升高和初始热应力对频率参数的影响等；王金朝[6]基于能量原理研究了不同板壳结构的振动特性，并通过对锥-柱-球壳组合壳体进行振动试验，验证了理论方法的可行性。

由以上研究可知，目前国内外学者对功能梯度矩形板、圆柱板等结构的振动特性进行了深入的分析，但对功能梯度圆锥板结构自由振动研究有待丰富。为此，本研究以功能梯度圆锥板为研究对象，基于一阶剪切变形理论开展一般边界条件下圆锥板结构自由振动特性研究，并探究材料和几何参数对其振动特性的影响，旨在为功能梯度圆锥板工程应用提供理论依据。

1 理论方法

1.1 几何模型

图1为功能梯度圆锥板几何模型，坐标系为O(s，θ，z)；圆锥板结构沿曲率s方向曲率半径为∞，垂直于曲率s方向半径为R = s·sinα0，沿s方向结构长度为L，沿θ方向转角为ϕ(0≤ϕ＜2π)，厚度为h。

图1 圆锥板结构模型与坐标系Fig.1 Structure model and coordinate system of functionally graded conical panel

1.2 运动学关系与应力合力

基于一阶剪切变形理论，功能梯度圆锥板任意点的位移分量由参考面位移和转角表示：

式中，u，v和w分别表示参考面上任意点在s、θ和z方向的位移；ψs和ψθ分别表示参考面法线绕θ和s方向的转角；t表示时间。

功能梯度圆锥板参考面应变-位移关系为

式中，A和B表示Lamé参数[7-8]，对本文圆锥壳结构而言，A=1，B=s·sinα0。

根据文献[9]和式（2）功能梯度圆锥板的几何方程，功能梯度圆锥板应力分量和应变分量之间的关系可表示为

式中，Cij（i，j=1,2,3,4,5,6）为弹性刚度系数，详细表达式可参考文献[9]。

通过将应力沿功能梯度圆锥壳厚度上积分即可得到力和力矩，根据广义胡克定律，用应变表示应力，最终可以将力和力矩用终面应变和曲率分量表示[10]，即

式中，Ns、Nθ和Nsθ为面应力，Ms、Mθ和Msθ为力矩，Qs、Qθ为横向剪切力，κ为剪切修正因子，其取值通常为κ=5/6。

由式（4）本构关系可知，功能梯度材料存在拉伸-弯曲耦合，但不存在拉伸-剪切耦合。Aij、Bij和Dij为拉伸、拉伸-弯曲耦合和弯曲刚度系数，其具体表达式为

式中，弹性常数Qij(z)为厚度方向z的函数，其定义如下：

本研究中功能梯度圆锥板由陶瓷和金属混合制成，杨氏模量E(z)、密度ρ(z)以及泊松比μ(z)沿厚度方向连续，可进行以下线性组合：

式中，下角标c和m分别代表陶瓷和金属，体积分数Vc遵循以下四参数幂律分布：

式中，p为幂律指数；a，b，c为材料参数。FGMI和FGMII的体积分数Vc在参考面z=0处对称，所有组成相的体积分数之和为1[8]，即

功能圆锥板应变能可定义为

功能梯度圆锥板动能函数可表示为

式中，

功能梯度圆锥板四边布置五组弹簧来模拟一般边界条件，其一般边界条件方程式如下：

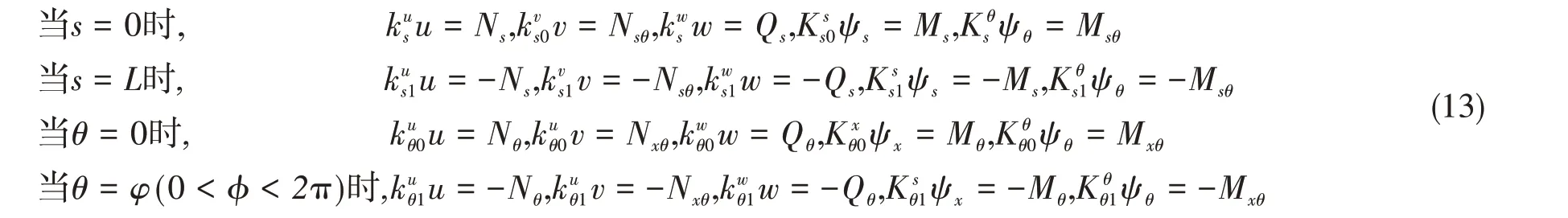
存储在边界弹簧中的势能Usp可表示为

1.3 位移函数

为克服边界的不连续性，本研究中位移容许函数采用改进的傅里叶级数来表示，不同位移分量可表示为

功能梯度圆锥板拉格朗日方程可表示为

将式（10）、（11）和（14）分别代入式（17），通过对未知系数求偏导可得

整理可得如下矩阵形式：

式中，K、M、和H 分别表示刚度矩阵、质量矩阵和未知系数矩阵。通过解方程（19）可获得功能梯度圆锥板结构的特征频率和模态阵型。

2 数值计算

2.1 收敛性研究和有效性验证

从理论表达式中可以看出，计算精度依赖于位移表达式的限制项数。因此，收敛性研究关键在于选择适当的截断项，同时通过与已有文献对比验证本文方法的有效性。

（1）收敛性研究

不同边界参数下约束刚度Γ对弹性边界条件下功能梯度圆锥板频率参数的影响如图2所示。

无量纲边界约束参数Γϐ（ϐ=u,v,w,s,θ）为相应的弹簧刚度与参考弯曲刚度D 的比率，即Гu=ku/D，Гv=kv/D，Гw=kw/D,Гs=Ks/D，Гθ=Kθ/D，其中D=Emh3/12(1-μm2)为结构刚度系数。当Γϐ=0 时，边界自由；当Γϐ=∞时，边界刚固；Гu=101～105范围时，频率参数Ω 迅速增加，为弹性边界条件。本文以下算例中各种边界条件通过表1功能梯度圆锥板弹簧刚度值确定。

图2 基频参数Ω随功能梯度圆锥板弹性约束参数的变化Fig.2 Variation of Ω versus Γ for functionally graded conical shell

表1 一般边界条件下圆锥板弹簧刚度值Tab.1 Corresponding spring stiffness values of conical shell for general boundary conditions

表1 中，F、C、S、Ei分别表示自由、固支、简支及弹性边界条件。

功能梯度圆锥板不同截断系数下前三阶频率参数的收敛性情况如图3所示。从图3中可以看出，所提出的统一方法收敛速度快，稳定性好。鉴于当前解的优良数值特性，本研究定义截断数M=N=15。

为进一步验证本研究方法的有效性，将本文结果与已有文献进行了对比分析，如表2 所示。由表2 可知，一般边界条件下，本文方法结果与现有文献结果一致性较高，表明本文基于收敛性分析成果，采用边界弹簧来模拟一般边界条件是可行的。

图3 圆锥板的频率参数Ω随截断数M、N的变化Fig.3 Variation of Ω versus M and N for functionally graded conical panels

表2 具有不同幂律指数p的功能梯度圆锥板的前九阶频率（Hz）的比较Tab.2 Comparison of the first nine-order frequencies(Hz)of functionally graded conical shells with different p

2.2 功能梯度圆锥板自由振动特性

在收敛性分析成果的基础上，计算得到一般边界条件下功能梯度圆锥板结构自由振动特性，如表3所示。

表3 具有不同边界条件的功能梯度圆锥板的前六阶频率参数Tab.3 First six-order Ω of the functionally graded conical panels with different boundary conditions

从表3 可知，同一模态参数下，功能梯度圆锥板自由边界振动频率参数较其它边界小，不同分布类型的频率参数相差不大，且第一类分布类型较高于第二类分布类型。不同边界条件下，功能梯度圆锥板模态阵型如图4所示。

为充分探究一般边界条件下功能梯度圆锥板结构和材料参数对自由振动特性的影响，本研究在收敛性分析的基础上，探究了结构厚度h、幂指数p和材料参数a、b、c等对功能梯度圆锥板自由振动的影响。

图4 不同边界条件圆锥板的模态形状Fig.4 Mode shapes for conical panels with different boundary conditions

（1）厚度h的研究

不同剪切修正因子下，结构厚度对功能梯度圆锥板自由振动特性的影响如图5所示。

图5 不同剪切修正系数圆锥板体的基频参数与厚度h的关系Fig.5 Fundamental frequency parameters of conical panels versus h with different κ

由图5 可知，具有不同剪切修正因子的功能梯度圆锥板板自由振动频率参数随结构厚度变化影响较大。同一剪切修正因子下，在一定厚度范围内，功能梯度圆锥板频率参数随结构厚度变化呈近似线性关系。剪切修正因子主要影响较厚功能梯度圆锥板的振动特性，对小厚度结构影响较小。

（2）幂指数p的研究

刚性固定条件下，不同幂指数p 对功能梯度圆锥板FGMI(a=1/b=0.5/c=2/p)和FGMII(a=1/b=0.5/c=2/p)自由振动的影响如图6所示。

由图6 可知，对两类功能梯度圆锥板而言，频率参数随幂指数增大呈总体减小趋势，在幂指数低值段，频率参数急剧减小，在高值段逐渐趋于平缓。同一幂指数下，不同类型功能梯度圆锥板频率参数差别较小。

（3）材料参数a、b、c的研究

材料参数a、b、c对功能梯度圆锥板频率参数的影响如图7所示。为方便研究，不同材料参数组合成以下四种类型，类型1：a=1，b=c=0；类型2：a=1，b=0.5，c=2；类型3：a=0，b=-0.5，c=2；类型4：a=1，b=1，c=4。

图6 功能梯度圆锥板FGMI和FGMII的一阶频率的变化Fig.6 Variations of the first-order frequencies of the functionally graded FGMI and FGMII conical panels

图7 不同材料参数对第一类功能梯度圆锥板频率参数的影响Fig.7 Influence of different material parameters on frequency parameters

由图7可知，不同材料参数对功能梯度圆锥板频率参数影响较大。p=5为四种功能梯度圆锥板频率参数变化趋势的拐点；类型1和类型2材料参数对功能梯度圆锥板频率参数的影响基本一致。因此，为避免结构共振，在进行功能梯度材料设计及应用中，应充分考虑材料参数对结构频率参数的影响。

3 结 论

本研究基于一阶剪切变形理论，采用改进傅里叶级数构造功能梯度圆锥板的位移容许函数，并通过里兹法探究了一般边界条件下功能梯度圆锥板结构的自由振动特性，研究成果可为相关理论研究及工程应用提供一定的数据积累。通过本文研究，得到了以下主要结论：

（1）数值算例方面，本文方法具有较好的收敛性和较高的求解精度；在收敛性方面，Γϐ=0时边界自由，当Γϐ=∞时边界刚固，Гu=10～105范围时为弹性边界条件，截断系数M=N≥10时圆锥板结构计算结果收敛；在计算精度方面，本文结果与已有公开发表的文献一致性较好。

（2）功能梯度圆锥板固有振动特性不仅与边界条件有关，而且与其自身材料属性有关，具有不同剪切修正因子的功能梯度圆锥板板自由振动频率参数受结构厚度影响较大，同一剪切修正因子下，在一定厚度范围内，功能梯度圆锥板频率参数随结构厚度变化呈近似线性关系；频率参数随幂指数增大呈总体减小趋势，在幂指数低值段，频率参数急剧减小，在高值段逐渐趋于平缓。