充液柔性接管轴向耦合阻抗理论研究

苏明珠，孙玉东，王锁泉，郝夏影

（中国船舶科学研究中心船舶振动噪声重点实验室；江苏绿色船舶技术重点实验室，江苏无锡214082）

0 引 言

柔性接管是用于管路系统中位移补偿和减振降噪的重要元件，其动态特性的研究，对于管系振动噪声传递和响应计算分析及减振降噪效果实现至关重要。Pinnington（1997）[1]指出，通过降低波速，由编织橡胶构成的柔性管和波纹管能同时提供振动和声波的衰减。阻抗是连接激励和响应之间关系的动力学参数，可以反映元件本身的动力学特性。对于柔性接管而言，其弹性部分一般为橡胶或橡胶-金属（非金属）织物混合结构，其柔性管壁与管内液体介质存在较强的声振耦合效应。为了考虑柔性接管结构中振动波和流体介质中声波的相互耦合，全面反映柔性接管的声学特性，从而精确预报管路系统的声振传递特性和元器件的减振降噪效果，需开展充液柔性接管的耦合阻抗研究。

近年来，俄罗斯克雷洛夫国家科学中心Sokolov（2014）[2]和Popkov（2012）[3]分别进行了包含耦合阻抗在内的柔性接管全阻抗矩阵元素的理论和测试方法研究，其中Sokolov 给出了正交各向异性和粘弹性充液软管作为梁模型的阻抗矩阵元素的理论公式，Popkov给出了测量机械阻抗、声阻抗和两者耦合阻抗的测试装置和方法。针对包含软管的管路系统，Munjal和Thawani（1997）[4]根据管段传递矩阵，研究了软管对入射的弯曲波、纵波和声波的传递损失，以及软管材料弹性参数、阻尼参数和长度、管段数、壁厚、内径、弯管角度等各种因素对隔振和声衰减的影响。Drew 等（1998）[5]描述了包含协调器的柔性软管的理论模型，得到了管端压力波和流动波关系的频率相关阻抗矩阵，计算了完整系统的流体噪声特性。在国内，哈尔滨工程大学李帅军（2015）[6]对输流管路的流体-结构相互作用研究进展进行了较为全面的回顾。西北工业大学的樊泽明（2013）[7]回顾了直管和弯管的充液管道线性、非线性流固耦合振动模型及分析方法。对于软管类管路元件，孙玉东等（2004）[8]以弹性直管为对象，不考虑泊松耦合影响，给出了轴向、横向机械阻抗和声阻抗的解析结果。

本文在考虑泊松耦合的基础上，对充液柔性接管声阻抗、轴向机械阻抗及耦合阻抗进行了理论推导，与不考虑泊松耦合的阻抗结果进行了对比，分析了材料和几何参数等相关因素对轴向阻抗的影响。研究结果可作为试验测量的考核依据，并为试验装置的设计提供参考。

1 充液柔性接管轴向耦合阻抗的理论推导

1.1 充液柔性接管轴向耦合方程及其通解

管壁的纵波和内部介质的一维声波的耦合控制方程组为

式中：Fx、Ux、P 和Uf分别是管壁纵向力、管壁纵向运动速度、管路中液体动压力和管路中流体运动速度；A 和Ap分别是管道公称面积和管壁横截面积；E 和μ 分别是管道材料的杨氏模量和泊松比；x 为沿管路轴向坐标；ρp是管壁材料密度；ρf为管内流体密度；E'V为考虑管壁弹性修正后的体积模量。对于薄壁管，

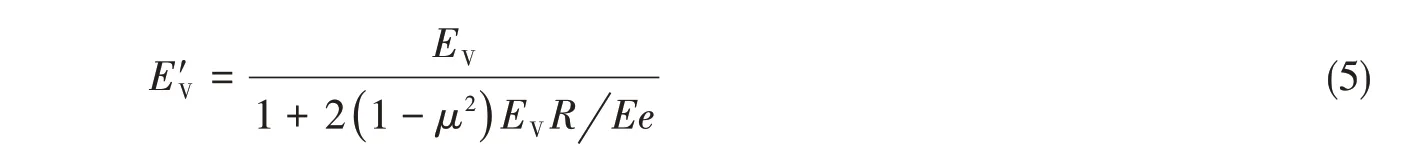
式中，EV为刚性管中流体的体积模量，R为管道的平均半径，e为管壁厚度。

对于式（1）～（4）所表示的考虑泊松耦合的声弹性梁柔性接管轴向方程，可采用以下无量纲形式：

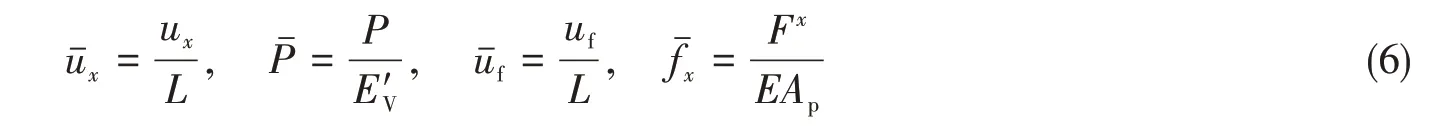
式中，ux为管壁纵向位移，uf为管道流体纵向位移，L为管长。

设时间简谐因子为ejωt，进一步采用以下无量纲参数：

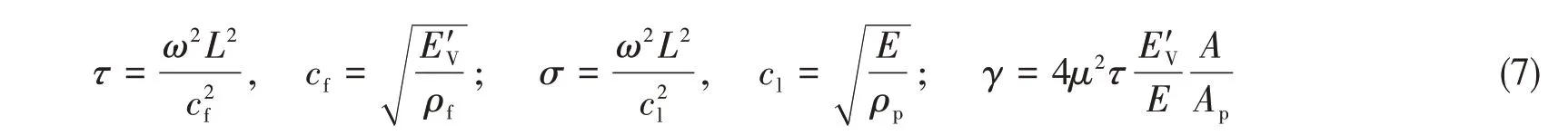
采用式（6）和式（7）中的无量纲变量和参数，假设沿轴向坐标的解有以下形式：

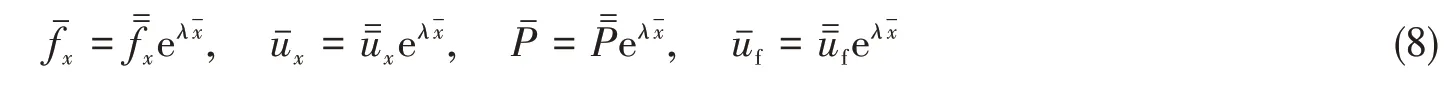
将式（8）代入式（1）～（4），得到λ的一元四次方程：

即对应于泊松耦合管道中结构和流体的无量纲纵波波数λ1和λ2，可按下式计算：

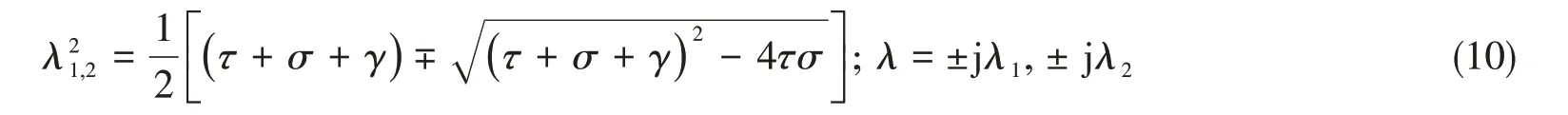
从而得到方程组的线性叠加通解为

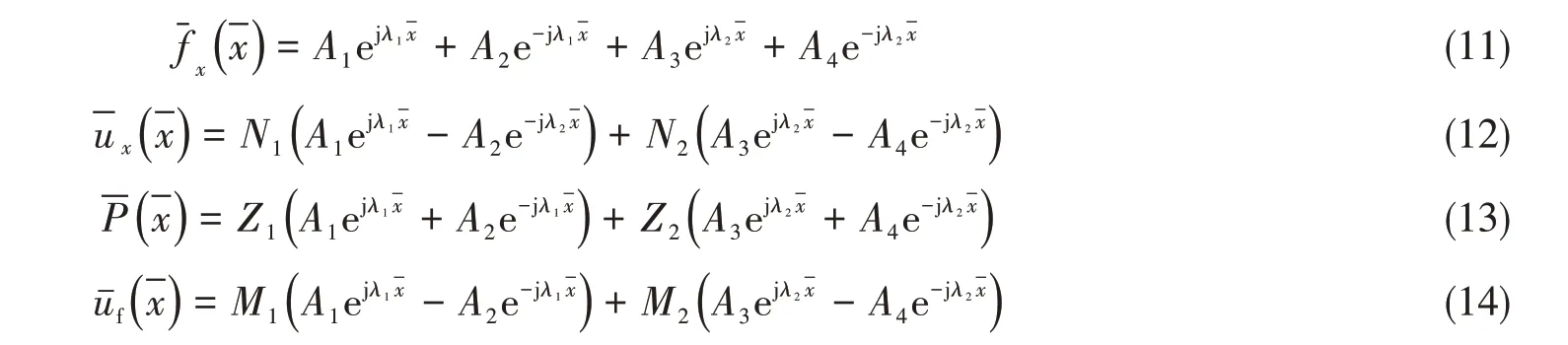
式中，

1.2 充液柔性接管轴向全阻抗矩阵及矩阵元素的推导

根据管路元器件阻抗的定义，两端状态量之间的关系以阻抗矩阵表示：

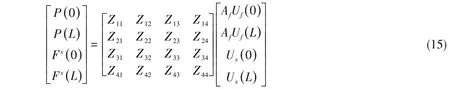
阻抗矩阵中各元素定义为

式中，Y为式（15）左端的激励力，X为式（15）右端的速度响应。

由式（15）和式（16），很容易得到入口端输入声阻抗为

出口端输入声阻抗为

即Z22= -Z11，表示柔性圆管两端的对称性。

声传递阻抗为

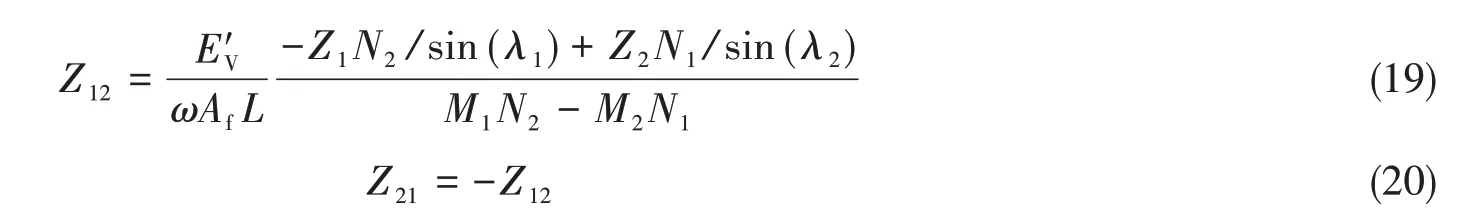
式（20）表示柔性圆管阻抗符合互易原理。

机械传递阻抗为

当μ ≠0，即考虑泊松耦合时，所有耦合阻抗矩阵元素的推导结果如下。

声-机械输入阻抗为

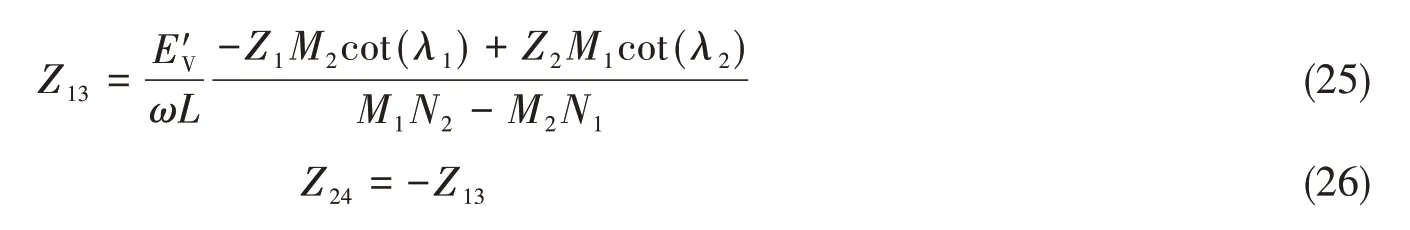
声-机械传递阻抗为

机械-声输入阻抗为

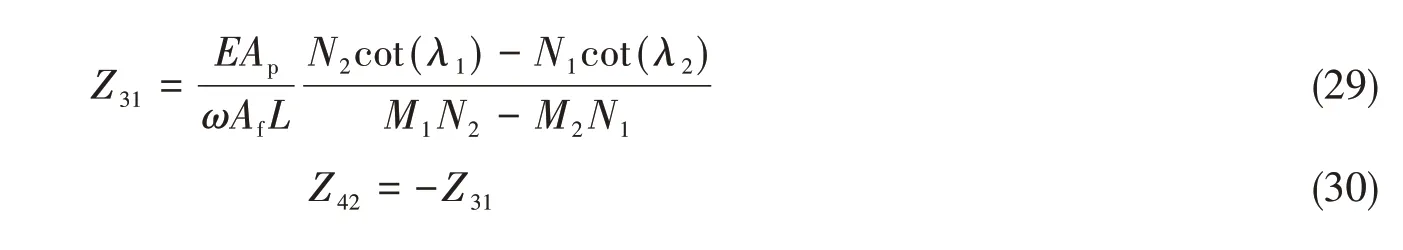
机械-声传递阻抗为

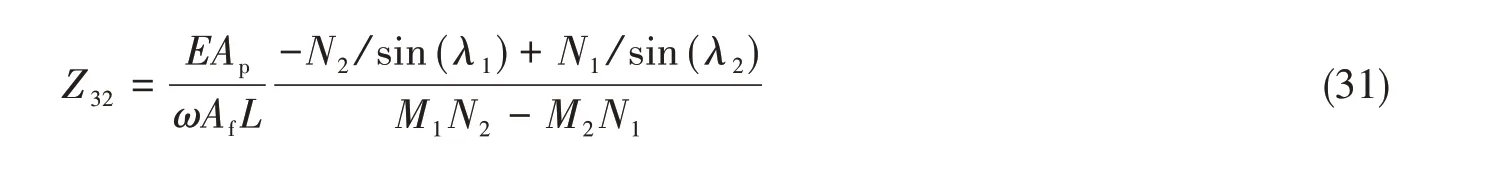
2 几何、材料参数对阻抗结果的影响

利用上面推导的公式，对充液柔性接管几何和材料参数变化下包含耦合阻抗在内的阻抗特性，进行MATLAB程序计算。基本计算参数如下：

式中：Qm,i为实测径流值，为实测径流平均值，m/s；Qs,i为模拟径流值，为模拟径流平均值，m/s。

水：ρf= 998 kg/m3，EV= 2.18 × 109Pa；

钢管：ρps= 7 800 kg/m3，Es= 2.1× 1011Pa，μs= 0.29；

橡胶管[8]：ρpR= 1200 kg/m3，ER= 3× 109Pa，μR= 0.48；

几何参数：L = 1 m，R = 0.05 m，e = 5 mm。

2.1 考虑耦合作用下橡胶管的各阻抗计算结果

由图1～4可见，考虑泊松耦合作用下的橡胶管的输入阻抗和传递阻抗在低频时吻合，在高频则出现差异。图1中声阻抗最小值所在频率，即反共振频率大约为100 Hz。图3中机械阻抗最小值所在频率约为450 Hz。图2中声-机械阻抗和图4中机械-声阻抗的输入和传递阻抗同样在低频重合，其中输入阻抗先共振再反共振，传递阻抗先反共振继而出现共振，声-机械阻抗和机械-声阻抗的共振频率接近，第一反共振频率在170 Hz左右。

图1 声阻抗Fig.1 Acoustic impedance

图2 声-机械阻抗Fig.2 Acoustic-mechanical impedance

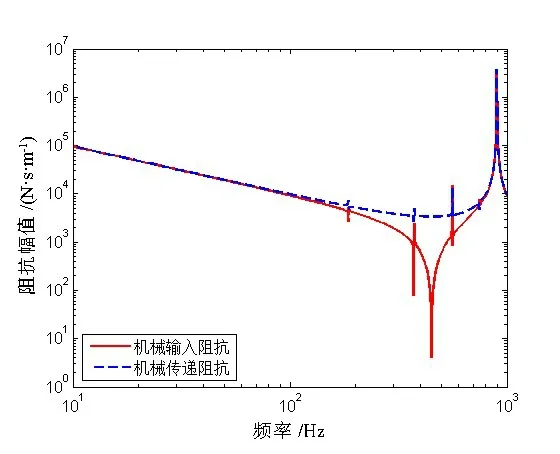
图3 机械阻抗Fig.3 Mechanical impedance

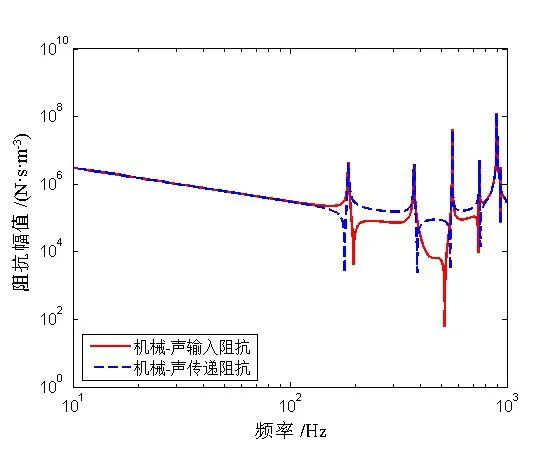
图4 机械-声阻抗Fig.4 Mechanical-acoustic impedance

2.2 考虑耦合与不考虑耦合橡胶管的阻抗结果比较

当不考虑泊松耦合时，柔性接管轴向阻抗矩阵只存在声阻抗和机械阻抗，声-机械阻抗和机械-声阻抗均为零。图5～8为考虑与不考虑泊松耦合的橡胶管的阻抗结果比较，从阻抗幅值来看，考虑耦合阻抗计算得到的阻抗值略高于不考虑耦合阻抗的。同时，考虑泊松耦合影响计算得到的声阻抗幅值-频率曲线会出现管壁结构共振频率，机械阻抗幅值-频率曲线会出现声共振频率，体现了二者的耦合影响。

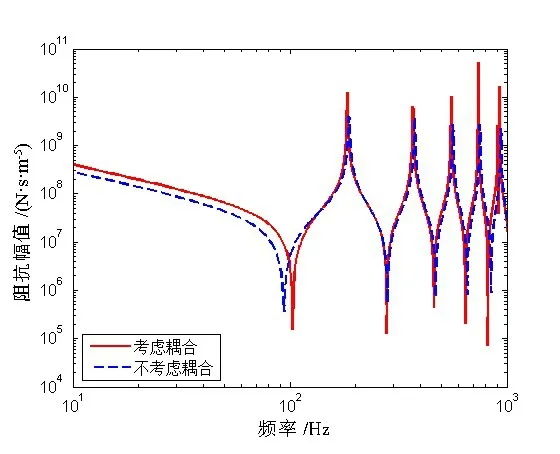
图5 考虑耦合与不考虑耦合橡胶管的声输入阻抗Fig.5 Acoustic input impedance comparison between coupled and uncoupled rubber pipes

图6 考虑耦合与不考虑耦合橡胶管的声传递阻抗Fig.6 Acoustic transfer impedance comparison between coupled and uncoupled rubber pipes

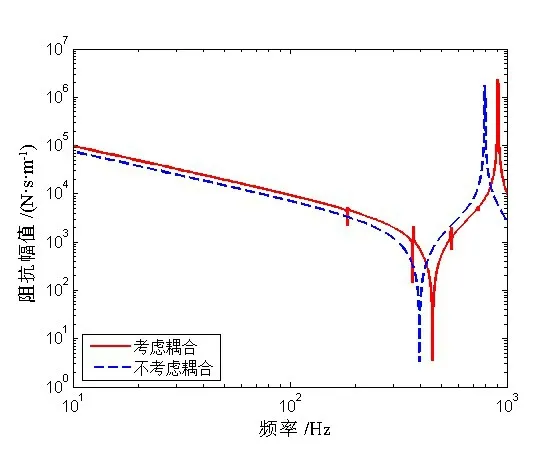
图7 考虑耦合与不考虑耦合橡胶管的机械输入阻抗Fig.7 Mechanical input impedance comparison between coupled and uncoupled rubber pipes

图8 考虑耦合与不考虑耦合橡胶管的机械传递阻抗Fig.8 Mechanical transfer impedance comparison between coupled and uncoupled rubber pipes

2.3 几何参数对阻抗结果的影响

图9～12为长度变化对橡胶管阻抗值变化的影响。可以看出，随着长度的增加，共振频率降低，反共振频率也随之减小。在低频范围内，充液橡胶管的阻抗值随长度的增加而减小。图13～16 为橡胶管口径变化对阻抗值的影响，声阻抗和耦合阻抗的共振与反共振频率随口径的增大而减小，机械阻抗与之相反。同样，在低频范围内，声阻抗和耦合阻抗值随口径的增加而减小，机械阻抗值随口径的增大而增大。

图9 长度变化对声阻抗的影响Fig.9 Influence of length variation on acoustic impedances

图10 长度变化对机械阻抗的影响Fig.10 Influence of length variation on mechanical impedances

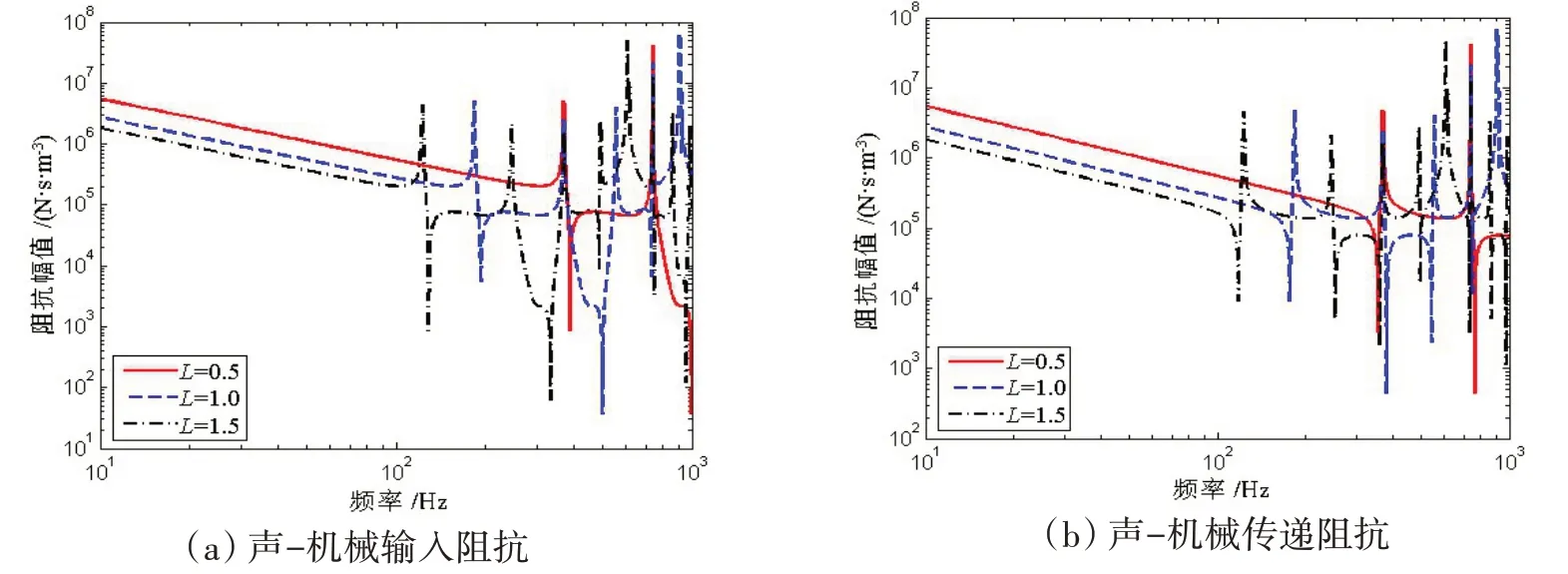
图11 长度变化对声-机械阻抗的影响Fig.11 Influence of length variation on acoustic-mechanical impedances

图12 长度变化对机械-声阻抗的影响Fig.12 Influence of length variation on mechanical-acoustic impedances

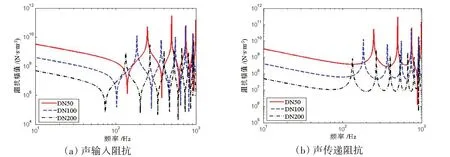
图13 口径变化对声阻抗的影响Fig.13 Influence of diameter variation on acoustic impedances

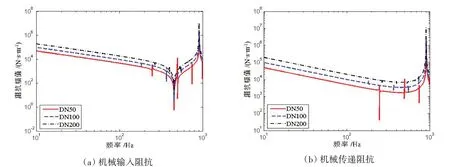
图14 口径变化对机械阻抗的影响Fig.14 Influence of diameter variation on mechanical impedances

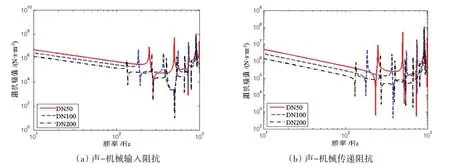
图15 口径变化对声-机械阻抗的影响Fig.15 Influence of diameter variation on acoustic-mechanical impedances

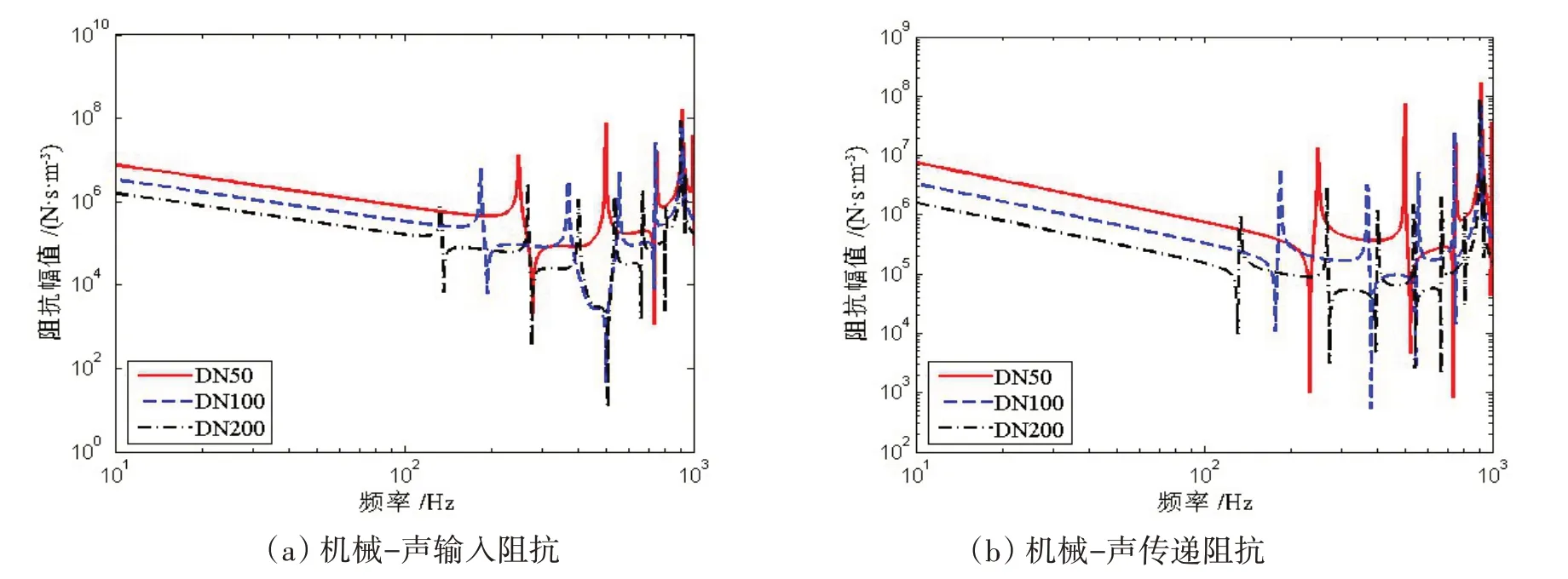
图16 口径变化对机械-声阻抗的影响Fig.16 Influence of diameter variation on mechanical-acoustic impedances

2.4 充液钢管与充液橡胶管的阻抗结果比较

图17～20是橡胶管与钢管的阻抗结果对比。结果表明，在低频范围内，钢管的阻抗值明显高于橡胶管的阻抗值，其共振频率也高于橡胶管。钢管的声阻抗最小值所在频率约为340 Hz，机械阻抗最小值所在频率超过1 000 Hz，声-机械阻抗和机械-声阻抗的最小值所在频率大约为630 Hz。

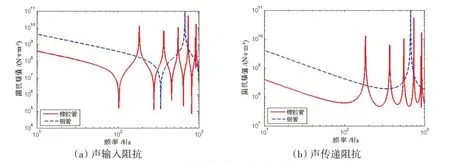
图17 钢管与橡胶管的声阻抗比较Fig.17 Comparison of acoustic impedances between steel pipe and rubber pipe

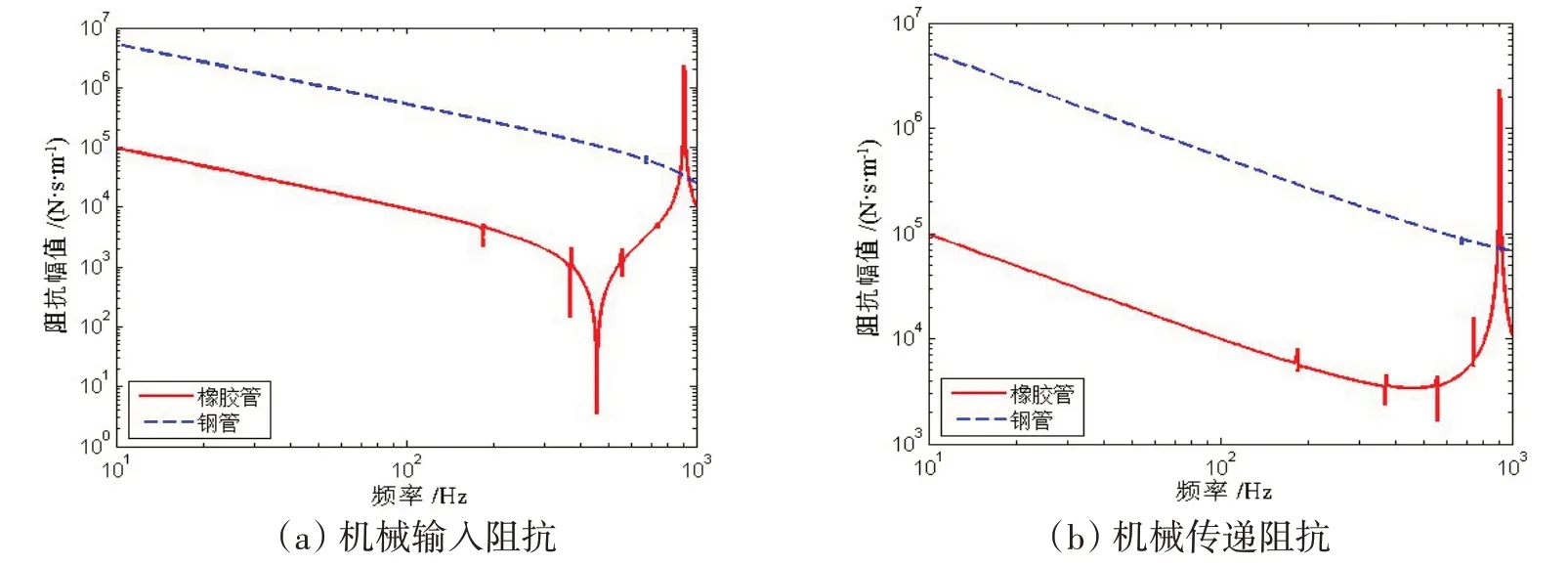
图18 钢管与橡胶管的机械阻抗比较Fig.18 Comparison of mechanical impedances between steel pipe and rubber pipe

图19 钢管与橡胶管的声-机械阻抗比较Fig.19 Comparison of acoustic-mechanical impedances between steel pipe and rubber pipe

图20 钢管与橡胶管的机械-声阻抗比较Fig.20 Comparison of mechanical-acoustic impedances between steel pipe and rubber pipe

3 结 论

本文根据充液柔性接管轴向耦合控制方程，推导获得了轴向阻抗的解析解，计算了各种相关参数对阻抗结果的影响，对比分析了考虑与不考虑泊松耦合及长度、口径、橡胶管与钢管材料不同时的阻抗计算结果，得出以下主要结论：

（1）充液柔性圆管轴向阻抗矩阵由声阻抗、机械阻抗和声-机械耦合阻抗、机械-声耦合阻抗等子矩阵组成，各子矩阵元素遵循对称性和互易性原理。

（2）耦合阻抗的算例表明，输入阻抗先共振再反共振，传递阻抗先反共振继而出现共振，声-机械阻抗和机械-声阻抗的共振及反共振频率接近。

（3）考虑泊松耦合时，声阻抗和机械阻抗会受到管壁结构共振与声共振的影响，直观体现二者的耦合作用。

（4）随着充液软管长度的增加，共振和反共振频率降低。充液软管口径的增大，导致声阻抗与耦合阻抗的共振与反共振频率减小，机械阻抗结果与之相反。钢管的阻抗值明显大于橡胶管的阻抗值，其共振频率也高于橡胶管，符合一般规律。

后续将对本文结果进行试验测量和验证，并对横向耦合阻抗、正交各向异性软管耦合阻抗等开展更多研究工作。