舱室防护装甲对战斗部破片群的防护效能评估

赵 传，王树山，李德聪，戴文喜，吴国民，周心桃

（1.北京理工大学爆炸科学与技术国家重点实验室，北京100081；2.中国舰船研究与设计中心，武汉430064）

0 引 言

绝大多数反舰导弹采用半穿甲战斗部，侵彻到舰船内部爆炸所产生的高速破片可对舰船内部结构、设备和人员造成严重毁伤，因此通常需要在指挥室、弹药库、燃油舱等重要舱室前设置防护装甲，以增强舰船的被动防护能力[1]。1999 年，世界船舶界权威认证机构英国劳氏船级社与皇家海军、国防部及其它政府机构合作成立了“LR 军舰技术委员会”，推出了《海军舰船入级规范》，简称“劳氏军规”，并每年进行修订，业已成为许多国家海军舰船设计、检验的参考和标准[2]。“劳氏军规”2017版[3]关于舰船重要舱室的防护装甲在面临反舰导弹打击时，需要防住初速小于1 400 m/s、质量不超过55 g 的破片，并给出了采用不同强度材质的防护装甲最小厚度。“劳氏军规”关于防护装甲的设计标准与规范，只是针对一种破片特例，能够一定程度上反映其防护能力。然而，对于不同的反舰导弹战斗部来说，其爆炸所产生破片的初速和质量分布存在显著差异[4]。因此，“劳氏军规”无法解决人们所关心的两方面问题：对于给定的防护装甲，如何定量表征与计算其对某一战斗部的防护效能并实现对不同战斗部防护效能的对比分析；如何针对防护的目标对象，依据防护效能要求设计防护装甲和抗爆结构。从防护设计角度考虑，降低穿透破片的分布密度即提高了目标的防护效能。因此，作用于目标的穿透破片分布密度可以作为目标防护效能的表征量。

本文提出了防护装甲的防护效能通过穿透防护装甲的破片分布密度进行定量表征以及四级防护等级划分方法；分析了厚壁壳体半穿甲型战斗部破片数随质量分布模型的适用性，论证了采用Weibull 分布模型的合理性；推导了考虑自然破片的通用侵彻公式，在此基础上给出了穿透破片的分布密度计算模型以及求解不同防护等级的防护装甲厚度模型。针对“捕鲸叉”及“飞鱼”反舰导弹战斗部进行了实例分析，获得了按劳氏军规设计的防护装甲所具有防护效能的定量分析结果以及达到不同防护等级分别需要的防护装甲厚度。

1 舱室防护装甲防护效能表征

反舰导弹战斗部内爆产生的自然破片对舱室的毁伤主要表现为穿甲作用，用命中防护装甲的穿透破片数量除以防护装甲面积可以得到穿透破片分布密度ρf，单位是枚/米2。李伟[5]从毁伤能力的角度出发将破片分为五个等级，由一级至五级破片毁伤能力逐渐降低。其分级思想具有借鉴意义，但若简单进行转换用于防护装甲的防护效能度量，意味着一级防护效能对应的穿透破片分布密度为0 枚/米2，尽管理论上是存在的，但工程上难以接受和实现；而五级防护效能对应的穿透破片分布密度为1 382 枚/米2，显然这样低的防护效能是没有实际意义的。

参考破片对装甲类目标毁伤律的研究结果[6-8]可以认为：穿透破片分布密度大于8 枚/米2时，目标毁伤概率趋近于1，相当于装甲防护效能极低或未起到有效防护作用；穿透破片分布密度为2～8 枚/米2时，目标毁伤概率显著下降，装甲起到了防护作用，具备一定的防护效能；穿透破片的分布密度小于2 枚/米2时，目标毁伤概率很小，装甲具备较高的防护效能。基于此，本文提出一种针对防护装甲防护效能的四级划分法，从一级至四级防护效能逐渐降低，如表1 所示。当然，这种四级划分方法并不具有绝对的科学性，还可以有其他的分级方法，这里主要是展示一种解决问题的基本思路，也使后面的模型建立和分析计算得以完成。

表1 舱室防护装甲防护等级Tab.1 Protection levels of cabin protecting armor

2 舱室防护装甲防护效能评估模型

2.1 破片数量随质量分布模型

自然破片的数量随质量分布目前主要按统计规律求得，但是试验中获取的破片质量分布数据往往是离散的，为了用于工程计算必须将离散数据连续化，因此普遍采用质量分布模型来描述自然破片的数量随质量分布。Mott质量分布是工程中应用最广泛的分布函数[9]，工程实践已经证明采用Mott分布可以很好地描述薄壁壳体破片的数量随质量分布。Grady[10]在Mott 破碎理论的基础上建立了基于能量的动态破碎理论，并且将统计学上常用于预测产品可靠性的Weibull分布用来描述破片的数量随质量分布：

式中，N(mf)是质量大于mf（g）的破片数；M 是战斗部壳体质量，单位是g；μ是Mott破碎参数，单位是g；Λ是破碎品质参数，其取值与破碎的均匀性有关。

典型半穿甲型反舰导弹，如“捕鲸叉”[11]及“飞鱼”[12]，其战斗部外径与内径之比均大于1.1，属于厚壁壳体战斗部。Mott 分布是单参数控制模型，其控制参数只能反映破片的质量特征；Weibull 分布是双参数控制模型，其中一个控制参数即Mott破碎参数，而另一个控制参数Λ能反映壳体破碎时的均匀性[13]，所以从理论上分析采用Weibull 分布来描述厚壁壳体战斗部破片的数量随质量分布更为准确。此外，文献[11]进行了一种厚壁壳体战斗部的破碎性试验，分别对比了Mott分布模型和Weibull分布模型的拟合结果，发现Weibull分布模型能更好地描述该战斗部的破片数量随质量分布。

综上所述，选取Weibull分布模型描述半穿甲战斗部的破片数量随质量分布更为合理。但目前工程上还没有较为成熟的方法用于预测Λ 的取值，一般需要设计破碎性试验或采用其他的方法得到具体战斗部破片群的Weibull分布模型。

2.2 破片平均初速及打击动能模型

战斗部爆炸产生破片群的实际初速是存在分布的，但是半穿甲战斗部的主体部分多为圆柱形，且普遍采用中心传爆药管结构，因此可以忽略初速分布，采用Gurney 公式[6]计算破片群的平均初速v0（m/s）：

破片在空气中飞行将受到空气阻力作用从而造成速度衰减，但是当飞行距离较短时破片的速度衰减可以忽略。因此假设内爆条件下破片的最终着靶速度为初速，在此前提下进行舱室防护装甲的设计有利于安全。综上，破片的打击动能Ek（J）为

2.3 自然破片侵彻公式

自然破片是依靠自身携带的动能对目标造成机械损坏，即形成孔穴或贯穿目标[6]。破片对装甲的破坏形式主要以冲塞破坏为主，其穿甲作用与破片着靶角度、破片质量、破片着靶速度等因素有关，出于安全考虑本文主要研究垂直入射情况下高速破片的穿甲效能。自然破片对靶板的侵彻是一个非常复杂的过程，想要精确分析必须考虑弹、靶两者相互作用时的弹塑性波、几何相容、有限应变和变形、超压流动、应变率效应、热效应、硬化效应和摩擦效应等[14]。目前主要有实验研究、理论分析和数值仿真等三类研究方法，但是还未得出一个通用的自然破片侵彻公式。Taylor[15]基于孔壁相似率和材料不可压缩性，建立了破片贯穿靶板所需的能量公式；Jordan[16]通过量纲分析及试验研究，发现破片着靶速度与破片质量、侵彻深度及展现面积呈线性关系。本文从能量角度出发，推导自然破片侵彻深度与材料性质、破片形状、质量及着靶速度之间的关系。

根据相关理论，自然破片对目标形成穿孔的打击动能应大于等于目标的动态变形功[17]：

式中，K1是无量纲系数；Sm是破片着靶面积，单位是m2；b是目标厚度，单位是m；σb是目标材料的强度极限，单位是Pa。

根据式（4）可以得到破片的最大侵彻深度δ为

式中，K1是一个与材料性质和打击速度有关的系数。试验统计表明[17]，对于靶板材料为硬铝（LY12），当打击速度不超过2 500 m/s时，

着靶面积Sm的计算比较复杂，实验表明，破片在飞行过程中作无规则旋转导致着靶姿态难以预测。因此着靶面积是随机变量，其数值应取数学期望值，研究表明着靶面积与质量存在如下关系[6]：

式中，ϕ是破片形状系数，对于长条形的钢制破片而言，ϕ = 3.55× 10-3m2/kg2/3。

当靶板为其他金属材料时，因为缺乏全面的侵彻试验作为支撑，无法得到针对每种材料准确的K1计算公式。对于这一问题，工程上常用的解决办法是采用强度相似原则[18]，将每种材料的靶板均等效为一定厚度的LY12，计算方法见式（8）。这种等效是以LY12作为标准，当靶板材料不是LY12，在面对同一破片侵彻时，材料的强度不同仅体现在破片侵彻深度的不同上，因此破片在侵彻不同材料时均可使用相同的系数K1，即K1-al。必须指出，这种等效方式与真实物理现象之间存在差异，本文所采取的是一种简化的工程计算方法，目的在于使后续的计算分析完整和收敛。

式中，σb-al是LY12的强度极限，σb-al= 4.61× 108Pa。

将式（3）、（6）～（8）代入式（5），得到考虑自然破片形状系数和靶板材料强度的通用侵彻公式为

式中，δm是自然破片侵彻靶板的最大深度，单位是m。

2.4 穿透破片的分布密度模型

变换式（9）得到：

式中，mi是能够穿透厚度为δm、屈服极限为σb的防护装甲的破片临界质量，单位是kg。针对不同反舰导弹代入不同的破片初速v0，可以求出穿透给定材质、厚度防护装甲的破片临界质量mi。根据式(1)，令mf= mi，得到该反舰导弹爆炸产生的破片质量大于临界质量的破片数N(mi)。

内爆破片群对防护装甲的作用情况与破片的空间分布、炸点与防护装甲的相对位置、战斗部姿态及牵连速度等因素有关，为了简化计算模型，做如下假设：

（1）忽略战斗部姿态以及牵连速度。若防护装甲距战斗部炸点距离大于10倍装药半径（对于“捕鲸叉”反舰导弹，10 倍装药半径约1.67 m），可忽略冲击波对靶板的毁伤，仅考虑破片的毁伤效应。认为破片着靶前在空间中的飞散形式为一个以炸点为球心的标准球面，并且质量大于临界质量的破片在飞散面上均匀分布。若防护装甲距炸点距离小于等于10倍装药半径，则破片飞散形式不是标准球形且有效破片的分布并不均匀。该情况下战斗部爆炸形成的冲击波是主要毁伤元，不可忽略，这种情况不在本文的考虑范围内；

（2）战斗部炸点与防护装甲几何中心的连线垂直于防护装甲所在平面，防护装甲长为2a（m），高为2b（m），防护装甲几何中心与炸点之间的距离为R（m）；

（3）除防护装甲所处的舱室壁面外，忽略其他壁面对破片群飞散方向的影响。

根据以上假设，得到的破片群飞散及与防护装甲交会情况如图1所示。

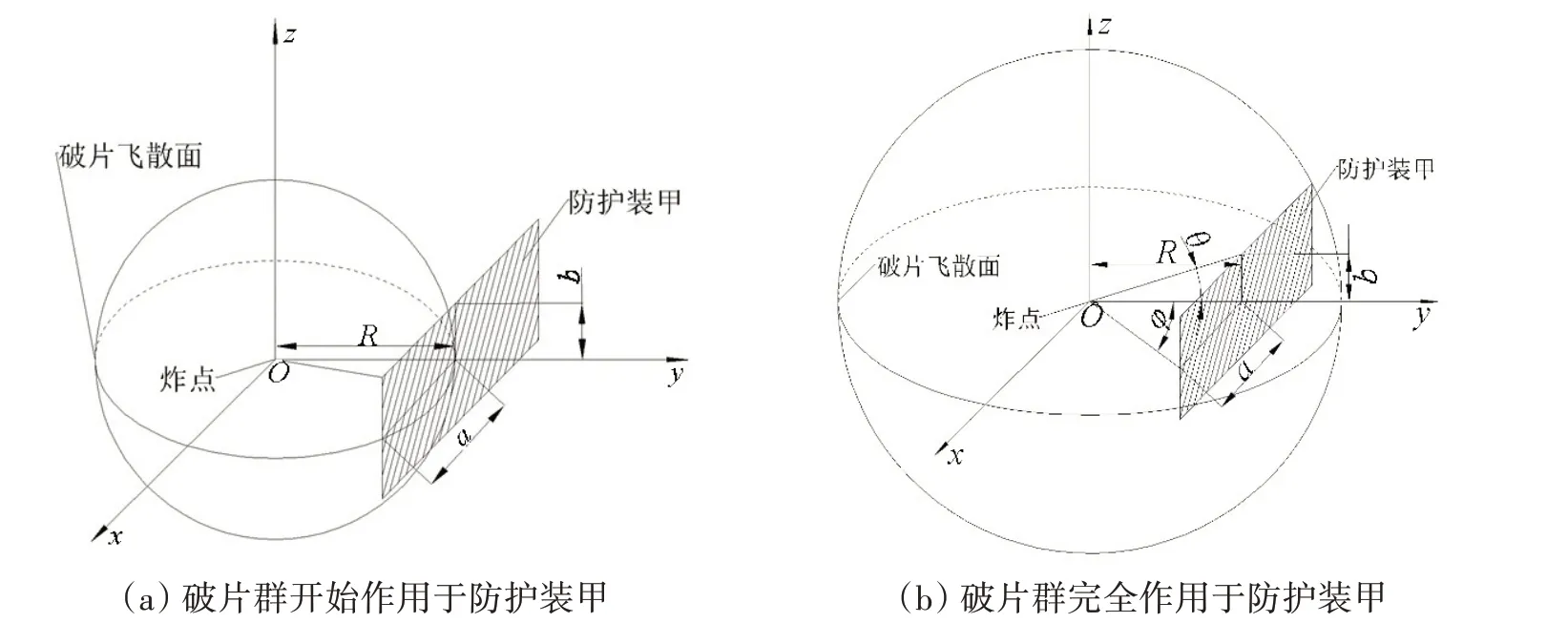
图1 破片群飞散及与防护装甲交会示意图Fig.1 Fragments scattering and impacting on protecting armor

根据图1（b），计算得到破片群完全作用于防护装甲时破片飞散面上的穿透破片分布密度ρm（枚/米2）为

作用于防护装甲的穿透破片数量，即为图1（b）中防护装甲在破片飞散面上的中心投影所包含的穿透破片数量，推导得到作用在防护装甲上的穿透破片密度ρf（枚/米2）为

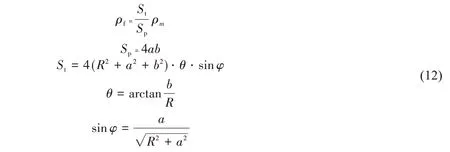
式中，Sp为防护装甲的面积，单位是m2；St为防护装甲在破片飞散面上的投影面积，单位是m2；θ、φ 分别为防护装甲的半高和半宽分别与炸点的连线与装甲轴线的夹角，含义如图1（b）所示。

2.5 不同防护等级的防护装甲厚度模型

根据预期的防护等级，得到对应的穿透破片分布密度ρf；给定防护装甲的几何尺寸以及炸点距离，采用式（11）和式（12）可以计算出内爆破片群中的穿透破片数N(mi)。应用式（1）可以得到针对不同反舰导弹战斗部，内爆产生N(mi)枚穿透破片对应的临界质量mi为

采用式（9），代入防护装甲的强度极限，令mf=mi可以求出不同防护等级所需要的防护装甲厚度δm。

3 实例分析

为了进一步说明舱室防护装甲对战斗部内爆破片防护效能评估模型的原理及意义，选取劳氏军规给定的防护结构作为评估对象，分别分析其在面临“捕鲸叉”及“飞鱼”反舰导弹内爆产生的破片群时的防护效能。

3.1 破片数量随质量分布计算

（1）“捕鲸叉”反舰导弹

调研文献[11]得到“捕鲸叉”反舰导弹战斗部爆炸产生破片的平均初速为2 181.20 m/s，破片数量随质量分布模型为

（2）“飞鱼”反舰导弹

根据文献[12]得到“飞鱼”反舰导弹战斗部爆炸产生破片的平均初速为1 812.00 m/s，破片数量随质量分布模型为

3.2 防护效能计算

设定典型大型舰船的重要舱室防护装甲长为10 m、高为2 m，炸点与防护装甲之间的距离为2 m。即式（11）和式（12）中a = 5 m，b = 1 m，R = 2 m。

（1）穿透破片的分布密度与防护等级

“劳氏军规”[3]规定：若使用RHA（轧制均质装甲钢）作为舱室防护装甲，防护结构厚度应为21 mm。根据相关文献[19]，RHA 的强度极限为σb= 1.65× 109Pa。应用本文建立的穿透破片的分布密度模型，代入相关参数，计算得到“劳氏军规”给定的防护结构在面对“捕鲸叉”及“飞鱼”反舰导弹内爆破片群时的防护效能如表2所示。

表2“劳氏军规”给定防护结构的防护效能Tab.2 Protective capabilities for protecting armor provided by LR’s regulation

从表2可以看出，“捕鲸叉”反舰导弹的内爆破片威胁大于“飞鱼”反舰导弹，若采用“劳氏军规”来设计舱室防护装甲，当面对“捕鲸叉”反舰导弹战斗部时，穿透破片分布密度为7 枚/米2，防护装甲的防护等级为四级；当面对“飞鱼”反舰导弹战斗部时，穿透破片分布密度为5 枚/米2，防护装甲的防护等级达到三级。

根据计算结果可以看出给定防护装甲对不同战斗部的防护效能差别，以穿透破片分布密度为表征量实现了对防护效能的归一化描述。所建立的计算模型实现了防护装甲对战斗部破片群防护效能的定量分析与评定，对重要舱室防护结构的防护效能评估具有应用或参考价值。

（2）不同防护等级的防护装甲厚度

根据“劳氏军规”的设计标准[3]，选择RHA 以及一种屈服极限为550 MPa 的材料作为舱室防护装甲。应用本文建立的不同防护等级的防护装甲厚度模型，令ρf分别为2 枚/米2、4 枚/米2、6 枚/米2和8 枚/米2，σb分别为1.65× 109Pa 和5.5× 108Pa，可以计算得到，针对“捕鲸叉”及“飞鱼”反舰导弹战斗部，达到表1所示防护等级对应两种材质的防护装甲厚度，如表3所示。

表3 不同防护等级对应两种材质防护装甲的厚度（单位：mm）Tab.3 Different protection levels corresponding to two kinds of armors’thicknesses(Unit:mm)

根据表3 的计算结果，如果采用RHA 作为防护装甲，当针对“捕鲸叉”反舰导弹时，达到一级防护效能需要防护装甲厚度大于30 mm；当针对“飞鱼”反舰导弹时，达到一级防护效能需要防护装甲厚度大于29 mm。如果采用屈服强度为550 MPa 的材料作为防护装甲，当针对“捕鲸叉”反舰导弹时，达到一级防护效能需要防护装甲厚度大于89 mm；当针对“飞鱼”反舰导弹时，达到一级防护效能需要防护装甲厚度大于88 mm。由此可见，所建立的计算模型可实现针对不同反舰导弹战斗部达到预设防护效能求解对应的防护装甲厚度，对舰船重要舱室防护装甲和抗爆结构设计具有应用或参考价值。

4 结 语

本文针对舰船重要舱室防护装甲的防护效能，提出了一种通过穿透防护装甲的破片分布密度进行定量表征以及四级防护等级划分的方法，建立了防护装甲防护效能的计算模型，对防护装甲对战斗部破片群防护效能的定量分析与评定以及重要舱室的防护装甲和抗爆结构设计，均具有应用或参考价值。