聚异氰氨酸酯唑烷酮的高应变动态响应研究

白晓军，张晓辰，赵 阳

(1.青岛国工高新材料有限公司，山东 青岛 266000；2.军事科学院 国防工程研究院，北京 100036)

分离式霍普金森压杆(SHPB)在1949年被Kolsky提出[1]，并取得飞速的发展并日趋完善[2-4]，最终成为在高应变率下研究材料力学行为的一项基本技术。高应变率下的材料本构关系研究是进行数值模拟的前提和必要条件，对于研究材料在冲击加载条件下的力学响应有重要意义。在恒应变加载条件技术的研究中，最早被提出和被研究的是脉冲整形技术，因此，此项技术在国内外都取得了大量研究成果。Duffy等[5]提出脉冲整形器思想并在后续实验中获得了比较理想的效果，该技术是在SHPB的基础上进行了改造，在扭杆冲击端前端黏贴薄片形整形片以实现恒应变。国内徐明利、卢芳云[6-8]等也从脉冲整形器的角度进行了研究，结果表明，SHPB存在的应力不平衡问题可以通过选择合适的整形器来解决。实验通过改变整形器材料材质和厚度来选择最优组合，并在一定程度上实现了加载恒应变率。Christensen等[9]在SHPB上应用脉冲整形技术，对岩石应力-应变曲线初始部分的分辨率和精度有了明显的提高和改善。南洋理工大学Lok等[10]通过把子弹的几何形状作为变量来研究脆性材料大尺寸SHPB的冲击力学性能，结果表明，相对于传统的矩形波，半周期正弦波加载对脆性材料动态力学性能的研究是较有优势的，在冲击力学实验中采用半周期正弦波形加载是消除应力波在波导杆中弥散的有效途径，此种波形上升沿平缓，可以从时间上保证脆性材料试样达到应力平衡，实验还通过计算机模拟和电算程序得到了子弹几何形状。李夕兵等[11-14]通过使用不同形状的撞击子弹对试样中应力、波形弥散等方面的影响做了研究，结果表明，使用双锥形子弹对于应力波弥散效应的消除具有明显效果，这主要是由于其作用过程中产生了具有较长的上升沿时间的半正弦波，并且使试样具有充足的时间建立应力均匀条件。这表明了半正弦加载波是岩石等脆性材料冲击性能实验的合理加载波。果春焕等[15]认为在SHPB实验撞击过程中减小产生的高频振荡可以利用波形整形，同时利用波形整形也可实现试样在受载过程中的恒应变率加载。该文还介绍了波形整形技术应用在SHPB的动态实验，包括压缩、拉伸、弯曲断裂等实验过程中应注意的问题。文献[16]基于脆性材料的SHPB实验数据，采用了数值模拟的方法进行研究，结果表明，利用SHPB进行脆性材料实验时应考虑惯性对材料的径向围压影响。

1 实验部分

1.1 原材料

POZD材料是青岛国人集团与青岛理工大学合作研发的新型材料(专利号:ZL 2015 1 0037147.2)，通过传统的喷涂设备[17]进行喷涂制样。

1.2 仪器及设备

SHPB系统：D145-75 mm型，合肥姜水动态力学实验技术有限公司；冲片机：MZ-4102型，江苏明珠试验机械有限公司；万能材料试验机：MZ-4000D1型，江苏明珠试验机械有限公司；附着力检测仪：Positest型，美国DeFelsko公司；邵氏硬度计：LX-A型，江苏明珠试验机械有限公司；喷涂机：H-XP3型，美国GRACO公司。

1.3 POZD动态响应实验原理

SHPB实验设备主要由4部分组成：发射系统、杆系统(撞击杆、入射杆、透射杆、吸收杆)、测试系统(应变片、应变仪和数据采集传输装置)以及阻尼系统。如图1所示，实验前将待测试样置于入射杆和投射杆之间的指定位置，撞击产生的应力波由测试系统取得并保存。

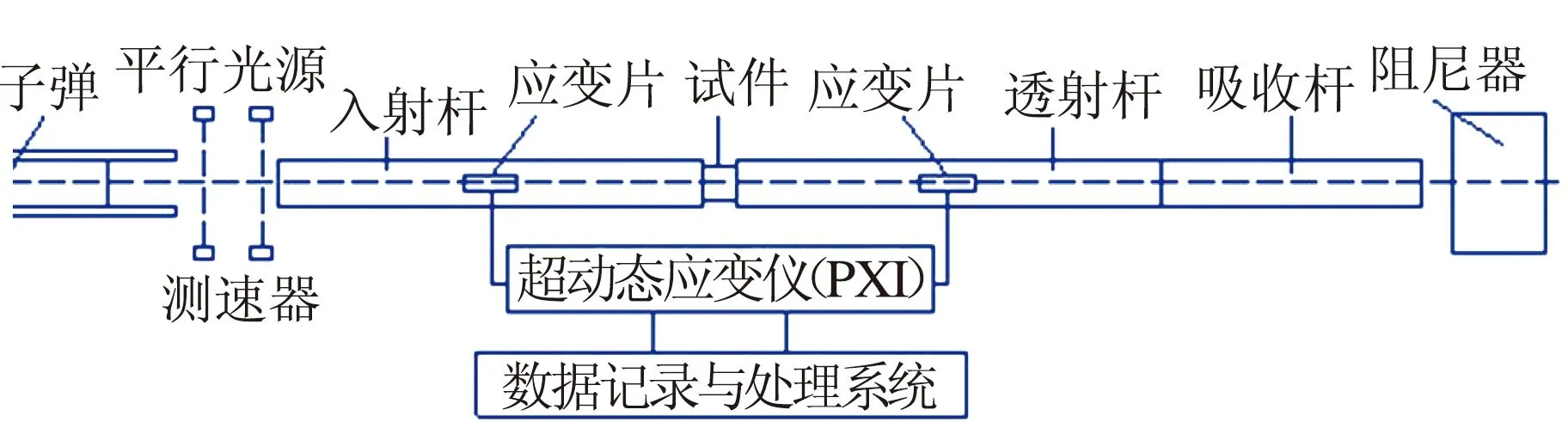
图1 动态实验装置

在实验过程中杆系统的物理参数和几何尺寸如表1所示。

表1 SHPB系统参数1)

1)d为直径；l为长度；E为弹性模量；ρ为密度；ν为泊松比；c为声速。

(1)

(2)

(3)

式中：εi、εr、εt分别为测得的入射波、反射波和透射波；c、E、A分别为压杆的弹性波速、弹性模量和截面积；A0和L0分别为试件的初始截面积和长度。式(1)～式(3)就是计算试样应变率、应力、应变的三波公式，反映试样的平均应力、应变和应变率。

试样两端面受力相等的状态下，可认为其内部各处的应力应变处于均匀状态。材料内部均匀状态下，三波公式变形简化为两波(以透射波和反射波计算)。本实验中，为保证试样有足够的时间在应力屈服之前达到内应力均匀化，且处理数据时简化为二波法，则通过整形技术来增加入射波上升沿的时间，保证材料在弹性阶段便达到恒定应变率，因此εi(t)+εr(t)=εt(t)成立，式(1)～式(3)可简化为式(4)～式(6)：

(4)

(5)

(6)

这样，只要试样内应力应变处于均匀状态，便可以根据应变片测量的反射信号和透射信号计算出试样的应力、应变和应变率。通过以上公式计算出的应力和应变实际上是工程应力和应变，在不可压的假定条件下，真实应力和应变与工程应力和应变之间的换算关系为式(7)和式(8)：

σr=(1-ε)σ

(7)

εt=-ln(1-ε)

(8)

1.4 POZD材料的SHPB实验

参照《GB/T 7314—2005室温压缩试验方法》和原材尺寸限制，设计动态压缩试件尺寸如表2所示。首先进行动态压缩实验，确定材料动态条件下的屈服强度，根据动态材料的屈服强度和应力波理论确定动态实验试件的尺寸。

表2 动态压缩实验方案

2 结果与讨论

2.1 SHPB实验结果

图2为不同应变率SHPB实验后采集的试件，可以看出，试件并没有明显的变形，尺寸也没有明显的变化。

(a)1 000 s-1

(b)2 000 s-1

(c)3 000 s-1

(d)4 000 s-1图2 实验后采集的试件

通过SHPB实验得到的原始波形如图3所示。

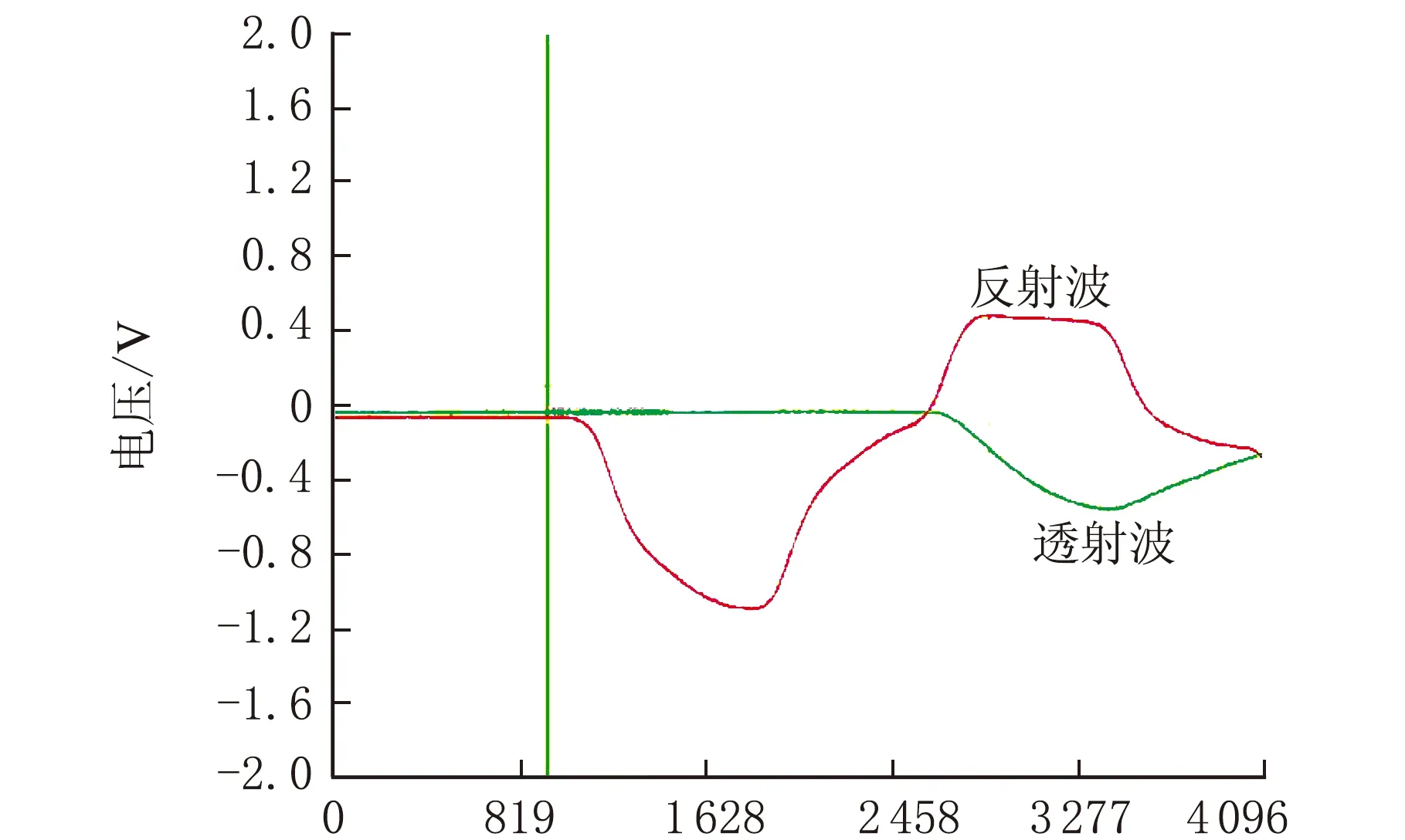
时间t/ms(a)1 000 s-1

把采集到的透射波和反射波信号经过对波等处理，导入MATLAB得到工程应变率曲线、名义应力应变曲线和真实应力应变曲线，如图4所示。

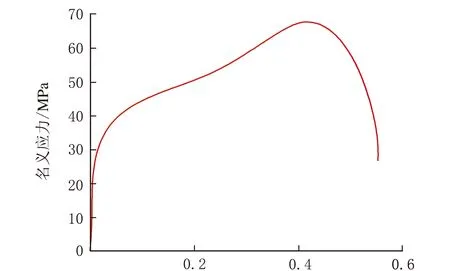
名义应变/%(a) 名义应力应变曲线

2.2 Mooney-Rivlin本构模型拟合

超弹性不可压缩材料的本构方程可表示为式(9)：

(9)

式中：σij为Cacuhy(真实)应力张量的分量，p为静水压力,δij为Korneker算符，W为应变能函数。下面假设取变形的主方向为坐标轴方向,则Cauchy变形张量用矩阵形式表示为式(10)：

(10)

式中：λi为i方向的主伸长比,λi=1+εi。εi为i方向工程应变主值,所以,Cij的不变量表示为式(11)～式(13):

(11)

(12)

(13)

λ2=λ3=λ-1/2

(14)

(15)

(16)

由式(16)解出p，代入式(15)得式(17)：

(17)

由图5和图6可以看出，由实验数据得出来的真实应力应变曲线与通过公式拟合的曲线吻合很好，可以得出该参数能较好地描述该种材料的动态力学性能。

应变/%图5 真实应力应变曲线

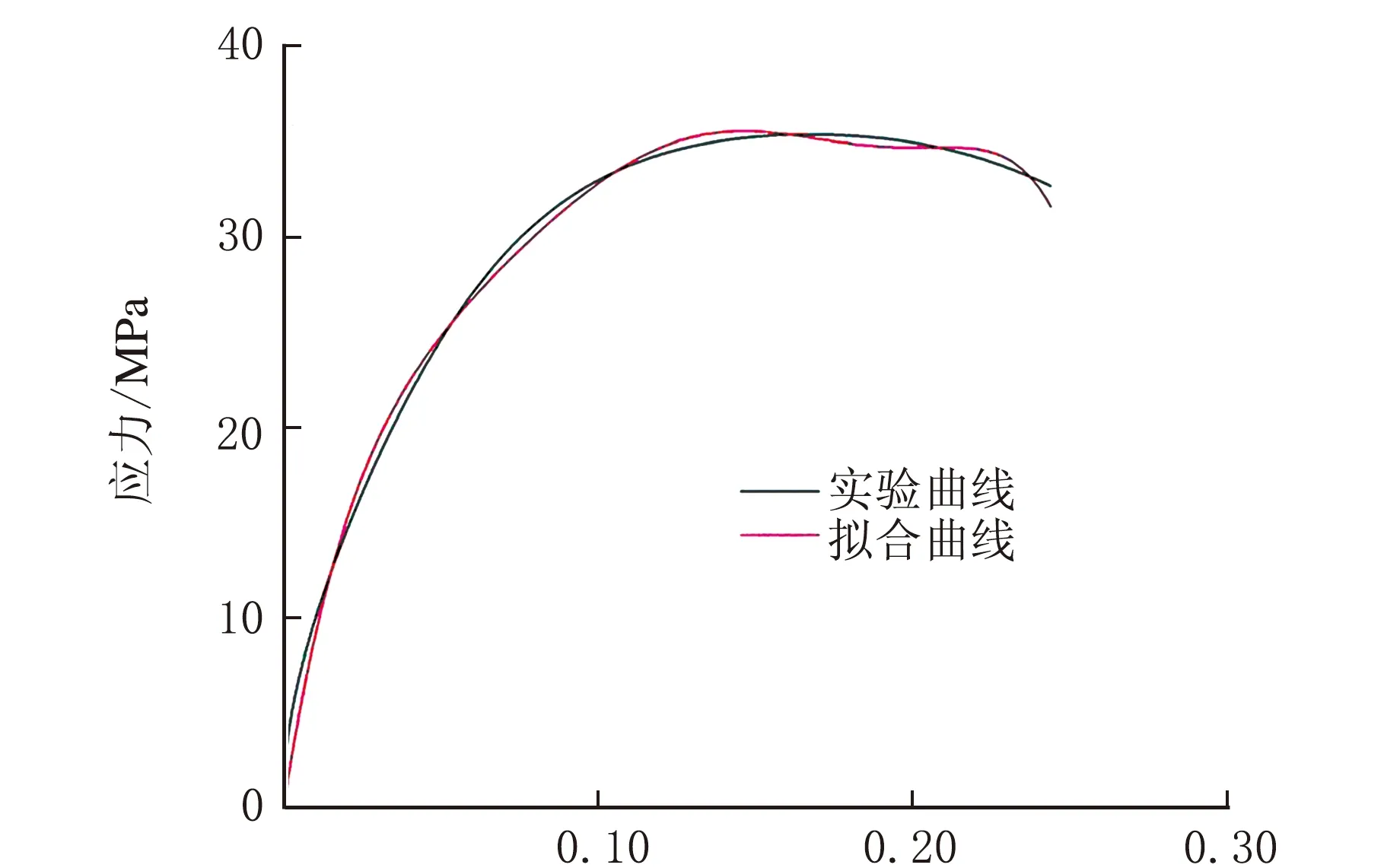
应变/%(a) 1 000 s-1

通过图6不同应变率拟合结果可知，实验曲线与拟合曲线存在一定误差，必须经过修正才能满足实际应用线。

3 结 论

(1)利用SHPB实验技术成功地采集到了POZD试件与压杆相互作用产生的反射波形和透射波形，对数据进行处理得到了应力应变曲线。

(2)根据实验数据应力应变关系拟合出POZD的Mooney-Rivlin本构关系。

(3)Mooney-Rivlin本构模型对POZD材料的应用设计和研究具有一定的参考价值。