基于ABAQUS炭黑填充天然橡胶Mullins效应的分析与比较*

王锐佳，刘广永，雍占福

(青岛科技大学 高分子科学与工程学院 橡塑材料与工程教育部重点实验室，山东 青岛 266042)

橡胶材料是一种具有高弹性的材料，具有优异的力学性能，在航空航天[1]、减振密封[2-3]、汽车轮胎[4-5]等领域有着广泛的应用。橡胶的很多性能与填料的分散程度有关，填料分散程度可以用Mullins效应来表征[6-7]。研究橡胶材料Mullins效应的方法很多，其中基于ABAQUS的有限元分析法因计算效率高和不受实验条件限制而具有高效便捷的特点[8]。王鹭等[9]基于ABAQUS研究了Yeoh本构模型、Ogden本构模型及伪弹性理论模型对炭黑填充天然橡胶Mullins效应的仿真效果及规律，并提出伪弹性参数与伸长比之间的关系，极大提高了计算效率。李凡珠等[10]基于ABAQUS，采用反分析法确定了炭黑填充橡胶Mullins方程的参数，并将Marlow超弹性本构模型、Mullins模型以及塑性变形理论相结合，精确地描述橡胶材料的循环加载与卸载条件下的应力应变行为。王晓明等[11]通过显式、直接的方法提出一个多轴可压缩应变能函数，用来模拟类橡胶材料在加载-卸载作用下，由于Mullins 效应而产生的应力-应变滞回圈。付宾等[12]研究了炭黑颗粒填充橡胶材料的本构模型，考虑到橡胶单个分子链与周围分子网络的约束作用和炭黑颗粒对橡胶的补强作用，提出了一种修正三链模型，并在修正三链模型的基础上，利用橡胶分子网络重构理论，提出了一种适合表征橡胶Mullins效应的本构模型。利用仿真计算所用的本构关系，可以进一步探讨高聚物凝聚态结构与性能的关系，不仅可以更深刻地理解其结构与性能的对应关系，还可以从定性的认识转为定量的描述，这项工作有一定的科研意义，也有重要的工程价值。

本文以炭黑填充橡胶的哑铃型试样为研究对象，利用ABAQUS和MATLAB最小二乘法确定Mullins效应的材料参数，并探究材料参数对Mullins效应的影响，以期更好地了解填充橡胶材料的损伤失效的过程。首先对哑铃型试样进行循环加载-卸载拉伸实验；然后提取加载段和卸载段应力应变数据，并计算出应变能和损伤变量；再基于MATLAB利用最小二乘法拟合出Mullins效应的材料参数；最后使用ABAQUS建立有限元模型，利用拟合得到的材料参数对炭黑填充橡胶的Mullins效应进行仿真分析。

1 Mullins效应概述

Mullins效应是指填充橡胶材料再次拉伸到某一应变时其应力小于初次拉伸该应变下的应力的现象，也称为应力软化。这一现象最初由Bouasse和Carrière[13]发现并报道，Mullins[14-17]进行了深入研究。图1(a)是Mullins效应的典型应力-应变曲线。填充橡胶材料受到初次拉伸时，其应力会沿着主加载曲线abb′cc′变化，当应变达到b′时进行卸载，其应力应变曲线会沿着曲线B变化；再次加载时，当应变小于b′时其应力会沿着曲线B变化，当应力大于b′时又重新沿着主加载曲线abb′cc′变化，往后的循环以此类推[18]。概括起来就是填充橡胶材料初次拉伸到某一应变时的应力总是大于再次拉伸到该应变下的应力。Mullins效应经典应力-应变曲线是一种理想模型，它并没有考虑塑性形变的影响。实际测试中，Mullins效应的应力-应变曲线如图1(b)所示,每一个加载-卸载循环之间有一段塑性形变，使主加载曲线不重合。本文的测试方法是:在每一次加载-卸载循环之后，将试样重新夹持，以排除上次循环产生的拉伸永久形变，得到实验应力-应变曲线，如图1(c)所示，其中主加载曲线OABCDE基本重合。

(a)Mullins效应典型应力-应变曲线 (b)有永久形变影响的Mullins (c)减小永久形变影响的Mullins 效应应力-应变曲线 效应应力-应变曲线图1 Mullins效应-应力应变曲线

2 橡胶材料的本构模型

2.1 超弹性本构方程及应变能函数

炭黑填充橡胶是一种具有交联网络和填料网络的复合材料，往往表现出复杂的力学行为，因而填充橡胶力学行为的本构关系十分复杂。目前，描述填充橡胶材料力学行为的本构模型是建立在诸多假设之上的，应用范围有限，因此很难找到一种能够描述所有填充橡胶材料力学行为的本构模型。所以，不同的填充橡胶材料需要找到合适自身的超弹性本构方程。

危银涛等[19]曾报道，目前常用的超弹性本构模型主要有基于热力学统计方法的本构模型和基于连续介质力学唯像理论模型两类。这些超弹性模型主要描述应变能和拉伸比或伸长不变量的关系。诸多文献[20-22]报道了超弹性本构方程选取策略，本文选用较为常用的三种本构模型(Polynomial模型、Ogden模型和Yeoh模型)来描述填充橡胶的本构关系，并从中选出最优的模型。

Polynomial模型、Yeoh模型和Ogden模型的表达式如式(1)～式(3)所示：

(1)

(2)

(3)

Polynomial模型描述的是应变能和力学不变量I1和I2的关系，当N=1时为Mooney-Rivlin模型，其材料参数是Cij。Yeoh模型是三阶Reduced Polynomial模型，其材料参数是Ci0。Ogden模型描述的是应变能和伸长比之间的关系，其材料参数是μi和αi。

橡胶材料在变形过程中三个力学不变量分别为式(4)～式(6)：

(4)

(5)

(6)

一般情况将橡胶材料视为体积不可压缩各向同性的材料，在单轴拉伸情况下，主拉伸λi(i=1,2,3)为式(7)和式(8)：

λ1=λ

(7)

λ2=λ3=λ1/2

(8)

将式(4)和式(5)代入式(1)～式(3)中，化简可以得到单轴拉伸情况下三种模型应变能与伸长比的函数关系。单轴拉伸情况下，Polynomial模型、Yeoh模型和Ogden的应变能函数为式(9)～式(11)：

(9)

(10)

(11)

2.2 Mullins模型

ABAQUS软件中描述Mullins效应的模型是基于Ogden和Roxburgh[23]的伪弹性理论提出的，该模型引入一个连续损伤变量η来描述Mullins效应，其表达式为式(12)：

(12)

式中：r、m、β为材料参数；W为加载过程中历史应变能；Wmax为加载历史中最大应变能；f为误差函数，其表达式为式(13)：

(13)

加载过程中，η不激活，为常数1；卸载过程中，η激活，随着卸载过程不断减小，完全卸载时，η达到最小值。损伤变量η还可以由名义应力定义[9]，其表达式为式(14)：

η=t/t0

(14)

式中:t为卸载过程名义应力；t0为加载过程名义应力。

3 实验部分

3.1 实验配方

实验配方(质量份)为：天然胶100，氧化锌2.5，硬脂酸2，炭黑N330 55，促进剂NS 1，硫磺3。

3.2 试样制备

按照上述实验配方，利用Haake转矩流变仪将生胶、氧化锌、硬脂酸和炭黑混合均匀，然后使用双辊筒开放式炼胶机将硫磺和促进剂加入并混合均匀；停放24 h后，使用RPA-2000橡胶加工性能分析仪，在151 ℃条件下测定上述混炼胶的硫化曲线；之后使用平板硫化仪硫化，得到100 mm×100 mm×2 mm的硫化胶片，硫化条件：温度为151 ℃，硫化时间为10 min，压力为12 MPa。

3.3 性能测试

根据GB/T528—2009，制备2型哑铃状试样，试样长度为(75±0.5)mm，测试区域长度为(20±0.5)mm，试样厚度为(2±0.2)mm。首先，使用电子拉力机以100 mm/min的速度将试样拉伸至伸长率为100%，并以相同速度恢复至原长，重新夹持试样以消除拉伸永久形变的影响。重复此过程将试样分别拉伸至伸长率为150%、200%、250%、300%处。

3.4 仿真计算

根据橡胶试样尺寸在ABAQUS/CAE中建立三维模型。经过几何建模、赋予材料属性、构建装配体、设置分析步、划分网格等操作后，得到图2所示的网格模型。整个模型共有3 960个单元(C3D8H)，5 772个节点。

为了尽可能模拟实验过程，本次仿真计算将试样夹持区域分别与参考点A、B耦合，模拟引伸仪夹持过程，设置边界条件时将B点完全固定，在参考点A上施加位移，位移方向沿X轴方向，模拟电子拉力机的拉伸过程。

图2 单轴拉伸试样模型及网格划分

4 结果与讨论

4.1 主加载应力-应变曲线的仿真

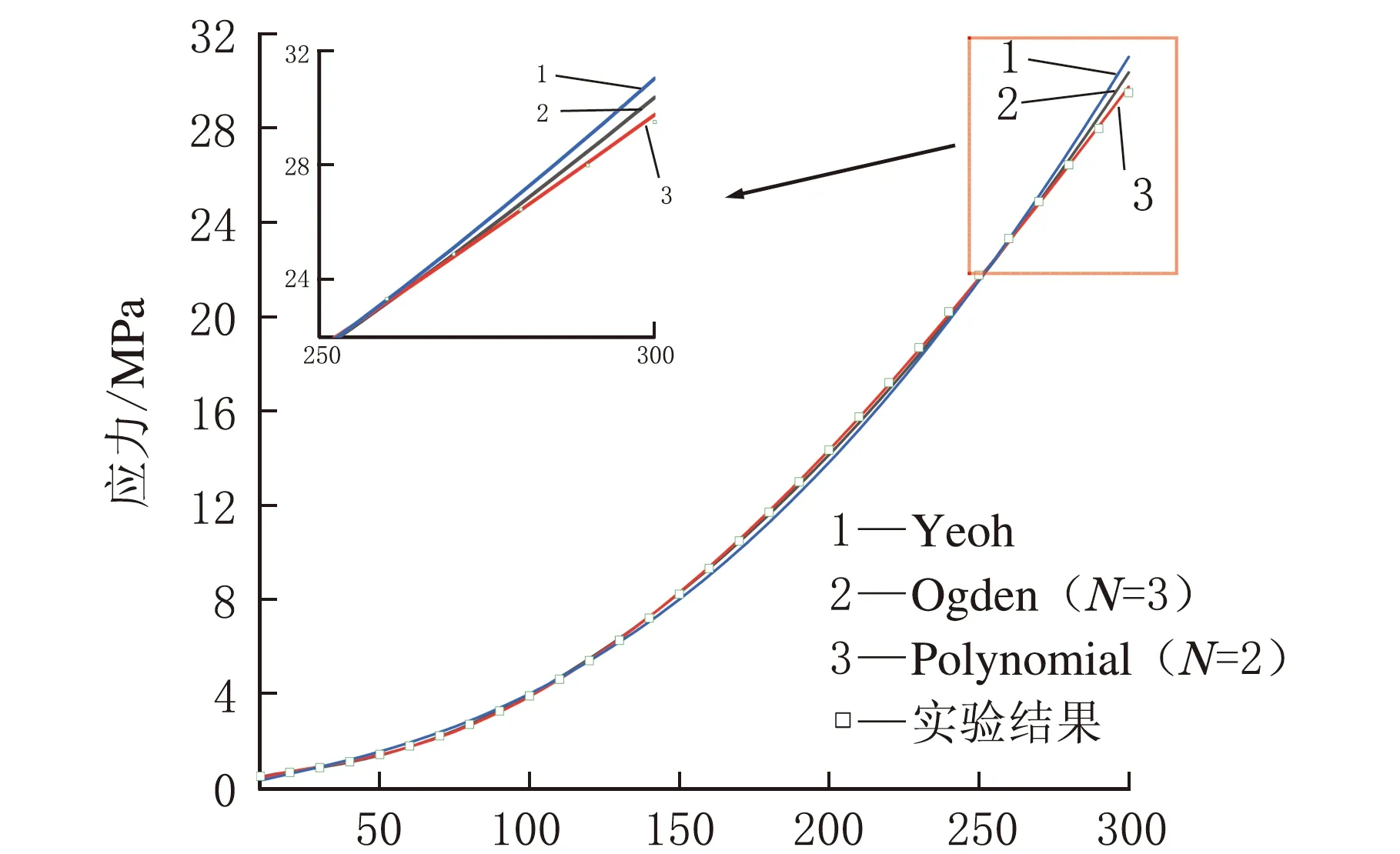
提取每一个加载-卸载循环与主加载曲线重合的加载段应力应变数据，将这些数据导入ABAQUS的Property模块中，使用Evaluate功能,并选用2阶Polynomial模型，3阶Ogden模型和Yeoh模型对实验数据进行拟合，结果如图3所示。

由图3可知，三种模型拟合效果都较好。其中，Yeoh和Ogden模型在小应变时拟合效果较好，当应变大于250%时，拟合结果明显偏离实验数据，主要原因为天然橡胶在大应变时，会出现应变结晶，导致应力陡升，而Yeoh和Ogden模型是基于第一力学不变量构建，不考虑材料的形状变化对力学性能的影响，对天然橡胶大变形条件下时出现应变结晶的情况进行修正。Polynomial模型在0～300%应变范围内与实验数据完全重合，拟合效果最好，主要是其引入了第二力学不变量对材料大变形时天然橡胶出现的结晶情况进行了修正。考虑到天然橡胶有应变结晶的情况，结合拟合曲线，本研究选用2阶Polynomial模型来定义材料的超弹性。表1为2阶Polynomial模型的材料参数。

表1 Polynomial模型的材料参数

应变/%图3 实验数据与拟合曲线对比

4.2 Mullins模型参数的计算与卸载应力-应变曲线的仿真

将4.1中拟合得到材料参数带入式(9)中，得到单轴拉伸条件下Polynomial模型应变能与伸长比的函数关系。将实验数据代入式(9)和式(14)，算出加载过程中的应变能W和损伤变量η。根据式(12)，使用MATLAB拟合得到Mullins效应材料参数r、m、β，其值见表2。使用ABAQUS进行有限元模拟分析，在Property模块中输入4.1中Polynomial模型材料参数和Mullins模型材料参数,设置相应的边界条件进行计算，结果见图4。

由图4可知，加载段上仿真计算曲线与实验数据完全重合。卸载段第4、5个循环的仿真数据与实验数据基本重合；第1、2和3个循环的仿真计算曲线在较大应变处与实验数据重合，在较小应变处与实验数据偏离，但小应变时应力较小，考虑到实验仪器的测量误差，仿真结果与实验数据的偏差在合理的范围之内；所以，本次仿真计算准确模拟了炭黑填充橡胶的Mullins效应。

表2 Mullins模型材料参数

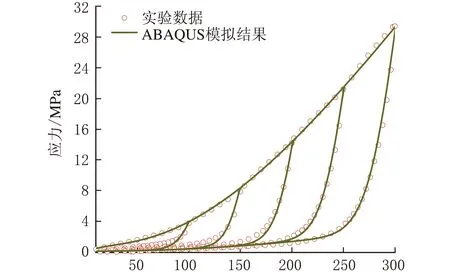
应变/%图4 Mullins模型模拟结果

4.3 Mullins材料参数对材料损伤行为的影响

4.3.1 材料参数r对Mullins效应的影响

保持参数m和β不变，当参数r=1.1、1.6、2.1、3.1、4.1和5.1时，利用ABAQUS计算出单轴拉伸情况下加载-卸载应力应变曲线，结果见图5。由图5可知，炭黑填充橡胶的Mullins效应的强度随着参数r的增大而减弱，并且随着r增大，减弱幅度减小。另外，参数r控制炭黑填充橡胶的初始损伤程度，即开始卸载时应力下降的程度，参数r越小，其斜率越大，损伤程度越大。由图5可以看出，填料网络的破坏随着应变的增加，刚开始时几乎都存在一段线性区，这个区域在加载和卸载过程中，填料聚集体的破坏程度在不同应变下，对材料模量的贡献相当，随着应变的增加，填料聚集体在同一应变下，加载和卸载时，应力变化加大，当应变继续增大时，应力变化反而减小，这种现象说明填料聚集体在材料变形时，常常是处于变形中间的某一形变时破坏得最严重；r越大说明填料分散得越均匀，在同样的变形条件下，填料网络破坏得很少。

应变/%图5 参数r对Mullins效应的影响

4.3.2 材料参数m对Mullins效应的影响

保持参数r和β不变，当m=1、3、5、7、10和15时，利用ABAQUS计算出单轴拉伸情况下加载-卸载应力应变曲线，结果见图6。

应变/%图6 参数m对Mullins效应的影响

由图6可知，随着参数m的增大，初始损伤速率逐渐减小。当m=1时，名义应力在极小的名义应变变化范围内下降到了一个趋于稳定的值；而当m=15时，名义应力经过200%～300%的名义应变变化范围才下降到一个趋于稳定的值。由图6可以看出，m从1到15，其标示的材料的损伤程度都较大，对比r而言，其可以对r的描述进行修正，m越小，对损伤的修正效果越明显。同样，m越大说明填料分散得越均匀，在相同的变形条件下，填料网络破坏得很少。

4.3.3 材料参数β对Mullins效应的影响

控制参数r、m不变，改变β，计算出β=0、0.2、0.3、0.4、0.5和0.6时的加载-卸载应力应变曲线。由图7可以看出，β从0.1到0.6，其标示的材料的损伤程度都较大，对比r而言，其也可以对r的描述进行修正，β越小，对损伤的修正效果越明显。同样β越大说明填料分散得越均匀，在同样的变形条件下，填料网络破坏得很少；然而相比较m来说，β的变化对网络的破坏性要高于m。

应变/%图7 参数β对Mullins效应的影响

5 结 论

(1)炭黑填充天然橡胶的Mullins效应是由r、m、β因素共同决定，可以通过其进行定量表示，其图像可以分解成r、m、β三个图像。

(2)炭黑填充天然橡胶的Mullins效应可以表征填料的分散情况，通过r可以定量地对其分散程度进行评价；若r相近时，可以依次通过β、m来比较。