一种加权变异的粒子群算法

徐 灯，傅 晶，王文丰，2，章 香，韩龙哲，2，方宗华，董健华

(南昌工程学院 1.信息工程学院;2.江西省水信息协同感知与智能处理重点实验室，江西 南昌 330099)

粒子群优化算法(Particle Swarm Optimization，PSO)是由Eberhart[1]等根据鸟群觅食行为所提出。PSO具有很好的生物社会背景，易于理解、参数少且易实现，在科学研究与工程实践中备受关注，譬如在路径规划[2]、图像处理[3]和洪水预报[4]等众多领域中都得到了广泛应用。然而，PSO算法却也存在着一些不足之处，例如容易陷入早熟现象、后期收敛速度较慢以及收敛精度不高等问题。

为此，国内外专家学者提出了许多不同改进策略的粒子群算法。Yan[5]等将随机学习机制与Levy飞行策略的特点相结合，在粒子的位置更新过程中，让粒子频繁短距离变换和偶尔长距离跳跃来提高种群的多样性。Chen[6]等引入正余弦加速度系数有效加强局部搜索能力，再对粒子进行反向学习，加入服从正余弦变化的惯性权重加速因子，提高了收敛的速度。文献[7]在速度更新方式中加入了局部最优位置，动态调整个体最优、局部最优以及群体最优在速度更新公式中的权重，改进了PSO算法的优化性能。Hao[8]等在改进粒子群算法时采用了算术交叉，共享粒子之间的信息来帮助早熟粒子跳出局部最优，提高了算法的精度。Zhao[9]等提出将种群分为正常和早熟两种状态，当种群处于正常状态按标准PSO公式进化，在早熟状态则引入矢量高斯学习策略以增强种群多样性。张强[10]等对种群的进化方式做了细分，结合了4种不同的方式使粒子进化具有自主性，提高了算法的精度和收敛速度。上述算法分别在粒子的位置更新、加速度因子、动态调整权重、种群的优劣划分等单方面策略对标准PSO算法进行改进，虽然都在一定程度上改善了粒子多样性、时间复杂度、易陷于早熟等问题，但是，大部分算法缺乏整体维度的考虑，在解决了粒子多样性等问题的同时可能增加了时间复杂度等问题，且均存在不同程度易于陷入早熟、收敛速度较慢以及收敛精度低的问题，特别是在高维函数优化问题上较为明显。

有鉴于此，本文提出了一种加权变异的粒子群算法(Weighted Variation Particle Swarm Optimization，WVPSO)。该算法引入自适应权重、自适应学习因子以及自然选择三种加速粒子收敛，算术交叉加权策略提高粒子的多样性以及高斯扰动增大粒子跳出局部最优的能力，并通过仿真实验对其性能进行了验证分析。

1 基本粒子群算法

PSO初始化为一群随机粒子，种群中的每个粒子都代表一个给定问题的潜在解。这些粒子通过调整飞行方向来引导自己，利用自身和其它群体成员的最优值来找到问题的最佳答案。

假设在一个D维的搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为Xi=(xi1，xi2，…，xiD)，第i个粒子的“飞行”速度记为vid，第i个粒子目前为止搜索到的最优位置称为个体最优值，记为：Pbest=(pi1，pi2，…，piD)，i=1，2，…，N；整个粒子种群目前为止搜索到的最优位置称为群体最优值，记为：gbest=(pg1，pg2，…，pgD)。得到个体最优值和群体最优值后，粒子便根据如下公式更新自己的速度和位置：

vid=ω×vid+c1r1(pid-xid)+c2r2(pgd-xid)，

(1)

xid=xid+vid，

(2)

式中的c1，c2为学习因子，也称加速常数；r1，r2为0～1之间的随机数。

2 WVPSO算法

针对PSO算法易于陷入早熟、收敛速度较慢和收敛精度不高等问题，本文提出了WVPSO算法，主要从以下三个方面进行改进：

(1)为保证算法寻优策略的全局搜索能力的同时平衡其局部搜索能力，本文提出一种自适应权重和自适应学习因子的方法，对式(1)中的权重w和学习因子c1，c2自动调整；

(2)为增加粒子种群的多样性、提高算法的搜索精度，本文提出一种加权变异的方法，在每次评估适应值后加入算术交叉和自然选择机制来改变粒子的位置和速度；

(3)对于算法易于陷入早熟的问题，在陷入早熟时加入高斯扰动，让粒子能够尽量地跳出局部最优值。

2.1 自适应权重和自适应学习因子

在PSO算法迭代的过程中，权重在算法迭代前期需要让粒子的步长变化更快，从而让粒子尽可能早地达到全局最优值所在的区域，而在算法迭代后期则应该减少步长的变化，让粒子在该区域内作精准的搜索使之找到全局最优解。对于学习因子，在算法迭代前期应该自我学习率占比高，群体学习率占比低；随着迭代不断进行，自我学习比率要逐步降低，而群体学习比率则逐渐提高。这样既可以加快算法的收敛速度，又可以提高算法的收敛精度。基于上述思想，本文提出了一种自适应权重和自适应学习因子的方法：

(3)

(4)

(5)

式(3)～(5)中，it和MaxIt分别为算法当前的迭代次数和最大的迭代次数；rand为0～1之间的随机数；c1up，c1low为自我学习因子的上下界；c2up，c2low为群体学习因子的上下界。式(3)中，权重w在算法迭代前期尽可能取最大值，从而使算法步长得到更快的变化；随着算法的不断迭代，权重则逐渐减小，以满足算法的自适应权重需求；式(4)在算法进行的过程中是一个递减的函数，式(5)则是一个递增的函数，符合自适应学习因子的思想要求。

2.2 加权变异

由于标准PSO算法收敛速度比较慢、迭代后期种群多样性降低，使得算法最后难以搜索到全局最优值。对此，本文加入算术交叉和自然选择策略来提高粒子多样性、增强收敛速度与精度。对于变异粒子的比例，通过以下方式选择：

[|P1|，|P2|，…，|PN|].

(6)

将所有粒子适应值的绝对值从小到大按照式(6)方式排列，并按照式(7)进行分割，式(7)如下：

(7)

将式(6)中的适应值分成ξ1，ξ2，ξ3，ξ4四个部分，由于粒子群算法存在的随机性，因此将粒子的适应值分为好(ξ1，ξ2)与不好(ξ3，ξ4)两个群体。其中ξ1，ξ4各占总体的20%；ξ2，ξ3各占总体的30%。这里使用交叉操作作用于ξ2，ξ3，融合好粒子与差粒子，不仅能够产生具有多样性的后代，而且促使差粒子向好粒子移动；使用自然选择作用于ξ1，ξ4，直接将差粒子ξ4的速度与位置直接替换为好粒子ξ1的速度与位置，类似于将整个种群缩小20%，从而大大加快粒子的收敛速度。具体策略如下：

(1)算术交叉：根据文献[11]的交叉公式，本文改进算术交叉公式如下所示：

xξ3=rand×xξ2+(1-rand)×xξ3，

(8)

vξ3=rand×vξ2+(1-rand)×vξ3.

(9)

xξ2，xξ3为式(7)中ξ2，ξ3处的粒子位置；vξ2，vξ3为式(7)中ξ2，ξ3处的粒子速度；rand为0～1之间的随机数。

(2)自然选择：通过选择好的粒子来替换差的粒子，增加粒子的收敛速度，具体方式如下：

(10)

xξ1，xξ4为式(7)中ξ1，ξ4处的粒子位置；vξ1，vξ4为式(7)中ξ1，ξ4处的粒子速度。

2.3 高斯扰动

随着算法的迭代，当全局最优值所在的区域远离当前种群的最优值时，粒子容易向错误的方向学习，此时粒子将极易陷入早熟。为了让算法跳出局部最优，在后期迭代时加入高斯扰动。如果当前适应值经过几次迭代后不再发生变化，则判断算法陷入早熟，这时加入高斯扰动，让粒子震荡，使其摆脱局部最优，因此在迭代初期加入高斯扰动策略。

2.4 算法流程

WVPSO算法流程如下所示：

Step1 随机初始化粒子的位置和速度，设定相关参数；

Step2 根据式(3)～(5)计算惯性权重w，学习因子c1和c2；

Step3 计算粒子群的适应值，根据适应值的绝对值从小到大按照式(6)方式排列，并使用式(7)分割；

Step4 使用算术交叉式(8)～(9)和自然选择式(10)策略将分割后的粒子进行重新替换；

Step5 根据式(1)～(2)更新粒子速度和位置，更新每个粒子历史最优位置pbest和群体最优值gbest。判断是否陷入早熟，如果陷入早熟则加入高斯扰动；

Step6若满足终止条件，则输出最优值，否则转入步骤(2)，进入下一次寻优。

3 实验与结果分析

为了验证WVPSO算法的性能，本文选取7种具有代表性的群智能算法进行对比，分别为：PSO，LinwPSO[13]，DGLCPSO[14]，PSOGSA[7]，AMBPSO[10]和(DE/best/1，DE/rand/1)[12]。实验环境为：Windows10操作系统，Intel酷睿i5处理器，主频3.2GHz，8G内存，开发工具为Matlab R2016b。

表1给出了7个经典的测试函数，其中4个单峰函数测试算法的收敛速度与收敛精度，3个多峰函数测试算法跳出局部最优的能力。各个算法的参数设置为：粒子种群个数为50；每个算法独立运行10次，每次实验最大适应度评估次数为1000；WVPSO的自身学习因子下限c1low=0.5，上限c1up=2.5，群体学习因子下限c2low=0.8，上限c2up=3.5。

表1 7个经典的测试函数

针对本文提出的3种改进方案，每一种改进方案均在标准PSO基础上做实验对比分析，记引入自适应权重和自适应学习因子改进的粒子群算法为ⅠPSO，引入算术交叉和自然选择机制改进的粒子群算法为ⅡPSO，引入高斯扰动改进的粒子群算法为ⅢPSO。其中对4个测试函数单峰和多峰函数做对比分析，结果如表2所示。

表2 不同算法的收敛精度及稳定性对比

图1给出了算法在函数f1，f2，f3，f4，f7寻优过程的迭代曲线，图中横坐标t表示迭代次数，fitness表示算法所得适应值。

由表2和图1可得出，无论在最优结果、均值还是方差上，3种改进方式都明显优于标准的粒子群算法。从3种改进的结果来看，引入算术交叉和自然选择机制改进的策略比另两种策略得出的结果精度要高出1～32个数量级，在函数f1，f2，f4的收敛速度上也是第2种策略更快，验证了本文采取的3种策略在综合性能上更佳。

由表3可以看出，WVPSO在7个测试函数上最优值、均值和方差都具有明显的优势。具体来讲，在单峰函数f1，f2，f3和多峰函数f4上，尽管WVPSO在最优值上没有达到极值0，但各个指标依相比其它算法优势明显，其中函数f1，f4在最优值上比AMBPSO算法至少提高了29和3个数量级，说明WVPSO在收敛精度和稳定性方面比AMBPSO算法要好，这得益于WVPSO采用自然选择策略，实现了快速收敛并优化粒子的目标，并且采用算术交叉保证了粒子的多样性和灵活性。在多峰函数f7优化上，WVPSO的最优值和均值都优于其它7个智能算法，只有方差微弱于AMBPSO；在多峰函数f5和f6上，WVPSO都能够在最优值上达到了全局最优值0，远远优于其它6个智能算法，在多峰函数f6优化上，虽然WVPSO和AMBPSO在最优值上达到了极值0，但本文算法均值与方差都为0，可以看出WVPSO对比AMBPSO在多峰函数f6优化上性能更加稳定。这说明了本文算法对复杂的多峰函数具有非常好的效果，即引入高斯扰动的粒子变异策略大幅度提高了粒子跳出早熟的能力。

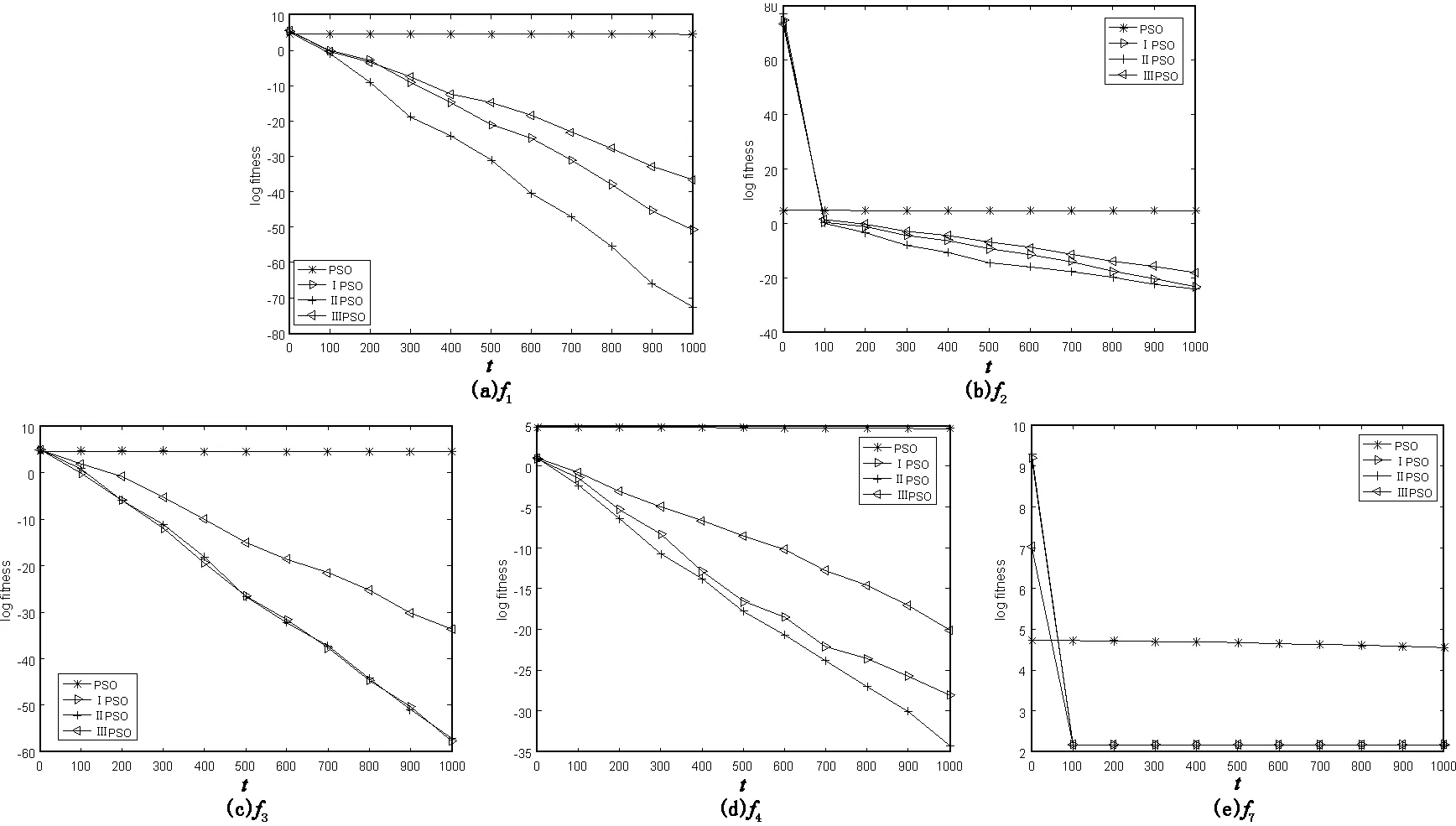
图1 各函数寻优曲线迭代图

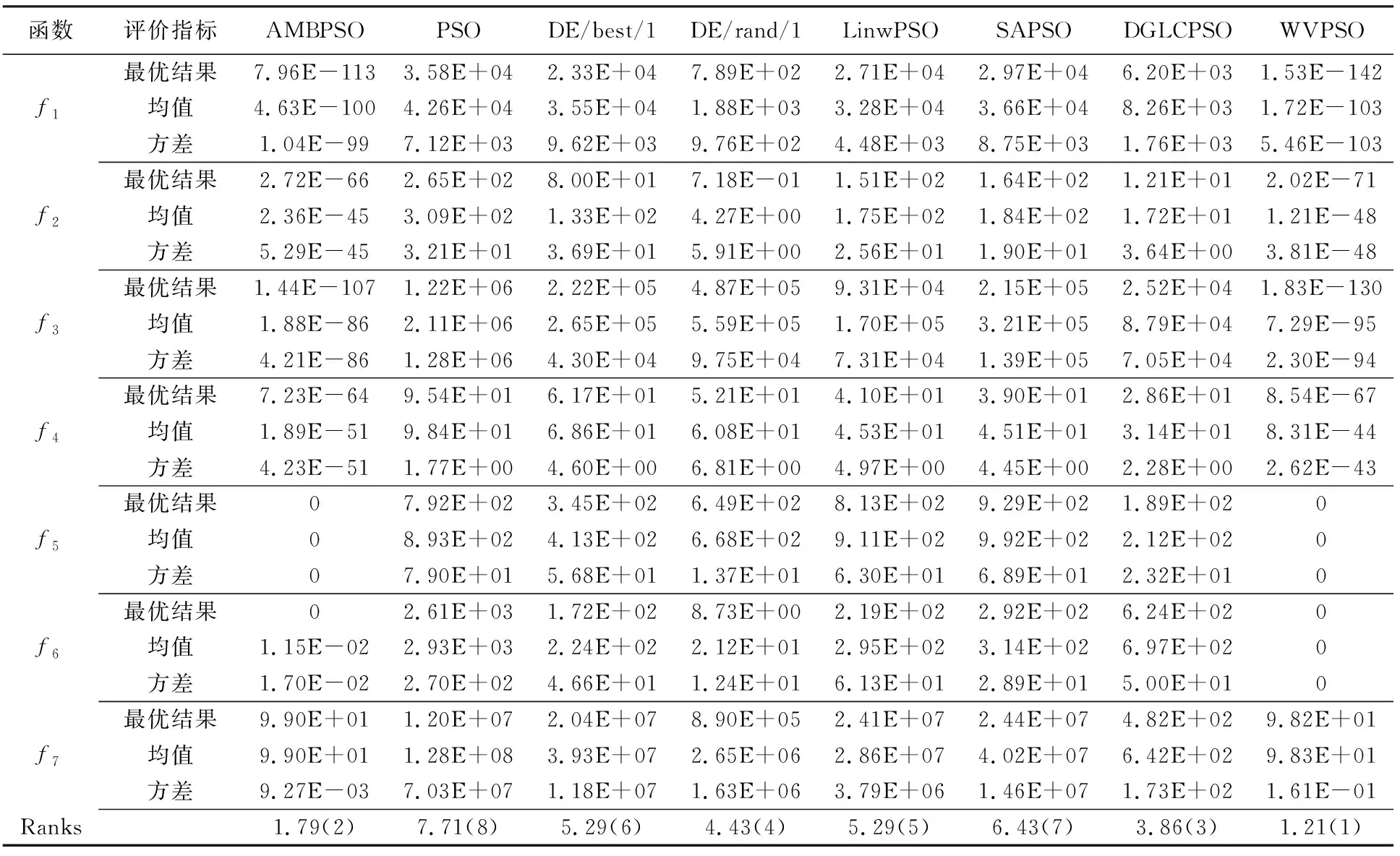
表3 不同算法的收敛精度及稳定性对比

对表3所得实验数据进行Friedman检验，所得结果中，WVPSO的所得秩均值评价指标最小(1.21)，验证了WVPSO算法的优化性能比其它7种智能粒子群算法更好，综合优化性能更强。

图2给出了不同算法在函数f1～f7寻优过程的迭代曲线，图2中横坐标t表示迭代次数，fitness表示算法所得适应值。从图2中不难发现，对比其它7个算法，WVPSO在收敛速度和精度这两个重要的评价指标上均有明显优势。在单峰函数f1～f3、多峰函数f4，f7上，虽然WVPSO和AMBPSO两个算法在最优值、均值和方差上无法作出准确比较，但是在迭代曲线图中可以清晰地看到，WVPSO迭代曲线的下降速度明显优于AMPSO的下降速度。其较好的收敛特性得益于算法采用了自适应权重和学习因子，使得粒子在算法迭代前期步长变化更快，能够尽可能早地达到全局最优值所在的区域。在算法迭代后期则减少步长的变化，让粒子在该区域内做精准的搜索使之找到全局最优解，同时自然选择策略使粒子的多样性提高，使得较差的粒子更多的向位置更优的粒子移动，极大地提高了粒子搜索效率；引入高斯扰动的粒子变异策略也加大粒子跳出局部最优的能力，从而保证了粒子的搜索精度。

图2 各函数的寻优曲线迭代图

综上所述，在处理高维函数寻优的问题上，对比其它7个群智能算法，WVPSO算法在精度、收敛速度和稳定性上都有着极大的优势。

4 结束语

本文针对标准PSO算法容易陷入早熟、收敛速度慢及收敛精度低的问题，提出了一种加权变异的粒子群算法WVPSO，通过对标准PSO算法粒子的位置和速度加权变异，以及惯性权重和学习因子的自适应调整进行改进，不仅增加了粒子种群的多样性，而且加快了算法的收敛速度，提高了收敛精度。从仿真实验结果可以看出，本文提出的算法均优于其它的几个群智能算法，在高维函数寻优问题的处理上具有很好的性能和稳定性，且在部分函数成功跳出局部最优，达到了全局最优值。但是本文算法并未完全摆脱陷入早熟的问题，如何更有效地使算法跳出局部最优将是下一步研究的重点。