颗粒破碎对岩土体宏观力学性能影响的细观机理分析

张 榜，丰浩然，吴 灿，陈 坤，陈雪嘉，张 鸿

(南昌工程学院 土木与建筑工程学院，江西 南昌 330099)

在实际的岩土材料中，在外力作用下总伴随着颗粒的破碎，进而土体结构重组，使得土体受力性能发生变化，所以有必要对颗粒的破碎机理及颗粒破碎后土体的物理力学性质进行分析。针对颗粒破碎，已有许多研究者通过室内试验和数值模拟做出了很多研究，获得了很多成果。

孔德志[1]等通过三轴试验人工模拟不同强度及不同粒径下堆石料颗粒的破碎，发现颗粒破碎可减小堆石体的剪胀和应变软化现象，同时对堆石体强度具有损伤和硬化的双重作用。刘新荣[2]等以不同含水率的土石混合体为研究对象，进行大型直剪试验及筛分试验，发现剪切试验后颗粒的破碎比较明显，并对颗粒破碎后的特征进行分析。张科芬[3]等通过PFC3D建立颗粒破碎模型，模拟石英砂、钙质砂、萨克拉门托河沙的颗粒破碎，并与实际试验进行对比，发现数值模拟与实际基本相符。徐永福[4]对垃圾炉渣颗粒进行破碎，并统计颗粒破碎的分维，总结了岩石颗粒破碎分维随破碎应力和破碎能量的变化规律。郭万里[5]等对粗粒土破碎耗能进行分析，并在Rowe剪胀方程的基础上推导出对粗粒土适用性较好的剪胀方程。刘萌成[6]等进行大型三轴试验，总结了土颗粒破碎的基本性质，对破碎渐进演化和进程进行分析。

洪俊[7]等为真实反映颗粒的破碎，改进算法提出一种基于离散元法的精细化破碎模型，可有效模拟颗粒破碎。刘苏[8]等提出改进一种模拟颗粒破碎的方法，适用于超级计算机计算，更好的模拟散体材料的应力-应变特性。张亚楠[9]等运用团聚体法生产球形单颗粒簇，系统性地分析颗粒的粘结强度、摩擦系数及局部阻尼系数对颗粒破碎的影响。雷晓丹[10]等通过PFC2D建立土石混合体的直剪试验模型，比较了不同块石粒径、块石形状、颗粒级配及最初孔隙率对颗粒破碎特性影响。Wang[11]等模拟单个颗粒破碎的情况，并分析了颗粒破碎对试样体积应变、塑性变形和剪切破坏的影响。Zheng[12]等在模拟滑坡过程中引入颗粒破碎，对颗粒破碎引起滑动面软化进行分析，发现颗粒破碎不仅会造成超孔隙水压力，而且会削弱滑动面的摩擦系数。

颗粒破碎机理极其复杂，特别对于土而言，实际试验很难监测其破坏情况，颗粒流模拟提供了一个很好的平台，可以模拟颗粒破碎，以及破碎前后其受力性能变化[13-14]。本文基于离散单元法，建立三维三轴试验模型，比较在伺服作用下可破碎的颗粒与不可破碎颗粒受力特点，从细观角度分析颗粒孔隙率、配位数的变化，结合颗粒旋转，能量变化对土体颗粒破碎的机理进行分析。

1 模型建立

在颗粒流模拟中，模拟生成球形颗粒会可降低建模难度和计算效率，不规则颗粒更接近于实际，这都提供了一种从细观层面了解颗粒物理力学性质的途径。在Fish语言建模中，不规则颗粒簇(clump)默认为一个刚性颗粒，在外力作用下不会产生破裂，这与实际的工程与试验相比有不一致。

柔性颗粒簇(cluster)是一些球体通过相互粘结而生成，其本质是可视作球体的组合，在超过自身粘结强度后，颗粒簇发生破坏，达到颗粒破碎的效果，可模拟岩土在外力下破碎特征。cluster在生成不规则刚性颗粒试样(clump)后，将整体clump转化为ball，同时在ball间施加粘结，最终将clump转化为cluster。cluster颗粒中ball间的参数如表1所示，其接触模型选用平行粘结模型，柔性簇颗粒间可传递力和力矩。

为更好比较颗粒破碎对其受力影响，clump与cluster间的颗粒参数一致，选用线性接触模型，颗粒间不施加粘结作用，其细观参数如表2所示。由于cluster颗粒重叠量较大，破碎时生成单个球形颗粒，体积膨胀，故孔隙率设置为0.45。

表1 柔性簇颗粒间的参数

表2 颗粒细观参数

本节通过建立三轴试验模型，生成不规则椭球颗粒模型，如图1所示，根据该颗粒模型生成土体试样，比较不破碎的刚性颗粒生成刚性簇试样(clump)，与可破碎柔性颗粒生成柔性簇试样(cluster)，在伺服加载下，两者的受力及颗粒细观物理力学变化。

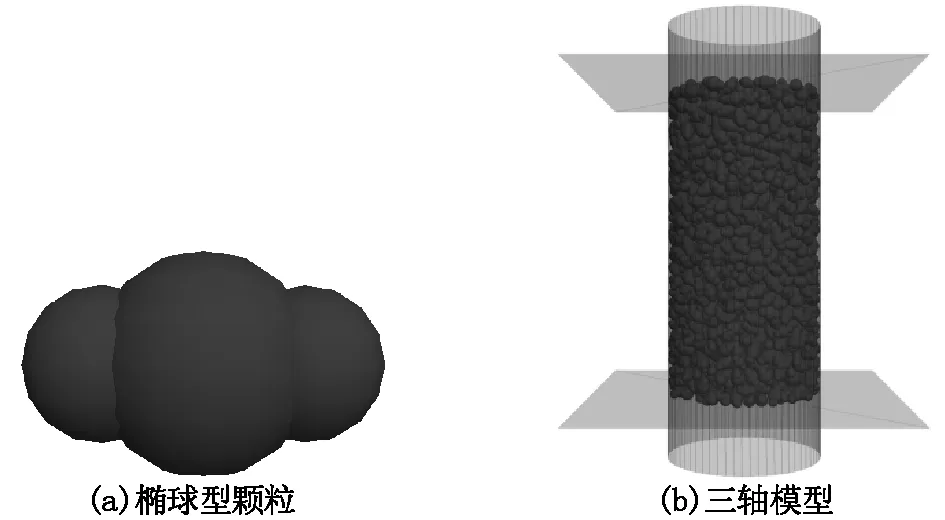
图1 模拟三轴试验

2 模拟结果及分析

2.1 颗粒破碎宏观力学分析

给clump试样和cluster试样赋予相同的参数、伺服加载，在相同围压下，得到两者的偏应力-轴应变曲线如图2所示。从图2中可以来看出，在初始加载至轴应变为0.06左右时，clump与cluster试样的受力基本一致；在轴应变为0.04后，两者受力发生变化，刚性簇的强度较柔性簇强度慢慢增大；在加载结束时，可以明显看出不破碎的颗粒比破碎颗粒的强度要大。由于使用线性接触模型，颗粒与沙石的性质相似，没有峰值强度。

从上分析可以得出，在加载力较小时，颗粒破碎较小，clump与cluster试样受力比较相似；随着外力加大，cluster试样内部颗粒逐渐破碎，其强度较clump逐渐减小，说明颗粒的破碎对试样的强度有影响。

图3为试样加载结束后的体积应变曲线，从图中明显可以看出，在整个加载过程中，cluster试样体积的减少就比clump试样体积应变要多；柔性簇试样在加载开始时其体积减小速率非常快，后逐渐减缓；刚性簇试样体积减少的速率较缓。这说明颗粒的破碎对试样整体体积的影响比较大，柔性簇内部颗粒在外力施加时会移动和破碎，填充掉内部孔隙较大的部分，致使试样体积减小较快，刚性簇颗粒整体受力，使得体积减小较少。

图2 偏应力-轴应变曲线 图3 体积应变曲线

从试样受力和体积变化可以分析，颗粒破碎对于试样的整体受力会有影响，相对于颗粒未破碎时，随着颗粒的移动、破碎增加，试样强度会降低，体积迅速减少，说明颗粒的破碎对试验整体的物理力学性质有很大影响。

2.2 颗粒破碎的细观作用机理

为了解刚性簇与柔性簇在受力时的物理力学特性，在三轴试样中心设置测量圆，以监测加载过程中配位数及孔隙率的变化。clump试样中生成2 080个刚性簇，颗粒受力施加于整个刚性颗粒；cluster试样中生成2 080个柔性簇，6 240个球形颗粒，颗粒的受力作用于单个球形颗粒，柔性簇只是给重叠颗粒施加粘结作用，在外力作用下，整个柔性簇内部各颗粒运动有不同作用。

为更好分析在颗粒破碎时土体内部变化，在两种试样内设置测量圆，得到两种试样内部配位数如图4所示，在达到指定的围压和轴压之后，开始加载。在初始时刻，clump颗粒的配位数就远大于cluster颗粒，随后在外力加载下，两种试样的配位数逐渐增大；在整个加载过程中，cluster试样的配位数都比较小。这说明在外力作用下，刚性簇试样颗粒间的接触比较好，颗粒结构相对更稳定，颗粒体系整体强度更大；而柔性簇颗粒间的配位数较小，颗粒间相互接触较差，结构稳定性较差。当然，这可能与颗粒的尺寸有关系，clump整体尺寸相对于cluster内部不同组成的球体尺寸要大。

clump试样与cluster试样的孔隙率变化如图5所示，在初始时刻，两者孔隙率基本一致；随着墙体开始加载，两种试样的孔隙率都开始下降，试样在外力作用下逐渐变得密实。从加载开始，cluster试样的孔隙率就比clump试样的孔隙率小；相比于clump试样，cluster试样孔隙率下降得比较快，加载结束后，柔性簇试样的孔隙率要比刚性簇试样小很多。这说明，颗粒破碎对试样密实度会有很大影响，结合体积应变曲线，柔性簇在外力作用下发生破碎，小颗粒会填充试样内部孔隙，导致试样体积变小，整体变得密实。

从测量圆监测的数据来看，两种试样的表现有很大不同，颗粒破碎后会使得颗粒间的接触变差，土体结构变差，对强度有不利影响；但颗粒破碎后会使得试样体积变小，试样变得密实，有助于颗粒体系整体受力。这与实际比较相符，砂石不易破碎，强度比较高；易破碎的土体，在外力作用下变得密实，其强度也会变高。

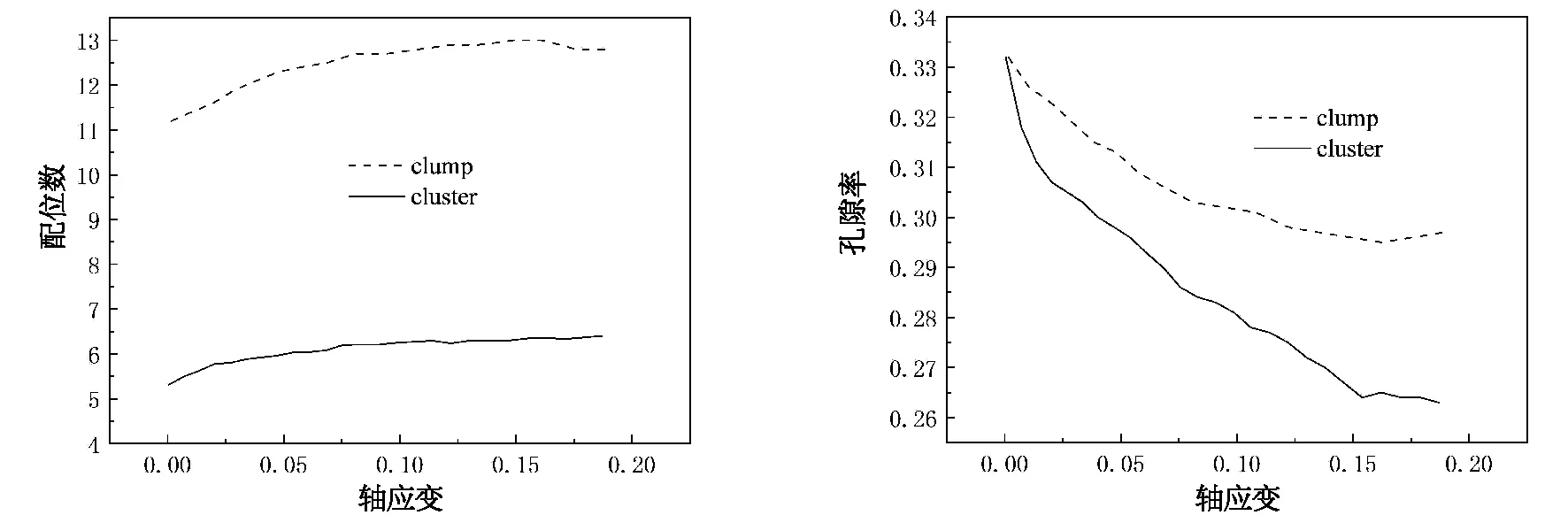
图4 配位数变化 图5 孔隙率变化

2.3 颗粒旋转分析

试样颗粒在加载时，其内部颗粒的移动和转动能反映试样整体稳定性及破坏情况，颗粒整体的转动角度越大，试样整体的稳定性也就越差。图6为两种试样在加载结束后整体颗粒的转动情况，黑色表示颗粒旋转角度较小，白色表示颗粒旋转角度很大。从图中明显可以看出，clump试样的体积略大于cluster试样，clump试样颗粒的旋转角度较小，同一刚体颗粒其旋转角度一致；cluster试样颗粒旋转情况十分明显，有部分颗粒发生破碎，形成单个球体颗粒，有部分颗粒在簇中的位置发生变化，部分柔性簇中，单个簇中各个颗粒的旋转角度也有不一致。

上述颗粒的旋转情况可以分析，刚性簇颗粒整体转动较小，在外力作用下试样整体结构相对比较稳定；在柔性簇中，簇内颗粒在外力作用下也会发生移动或转动，导致试样体积减小较大，试样内颗粒整体转动角度较大，使得土体结构变得不稳定，受力性质变差。这也说明刚性簇在受力方面优于柔性簇，柔性簇因颗粒破碎使得强度更低。

2.4 不同试样的能量分析

试样在外力加载过程中，促使内部颗粒发生运动进而产生能量。图7为加载过程中两种试样动能的变化，当墙体开始加载后，试样内部的动能急剧升高达到峰值，表明在这个时期，颗粒运动最为剧烈，产生的能量越大，由于产生动能之后会被耗散，使得动能的曲线显得比较波动。比较两种试样，cluster试样动能的峰值更大，且产生的动能始终比clump试样大，这表明在柔性簇试样内部颗粒的运动更剧烈，整体在外力加载下产生的变形更为明显，颗粒受力过程其内部结构变化更大，整体稳定性不好。

阻尼会耗散试样颗粒在运动、摩擦、冲击恢复和剪切变形等产生的能量[15]，进而使模型受力时能量变化归于平衡，计算变得稳定。图8为clump试样和cluster试样阻尼耗散能量的变化，在整个模拟试验过程中，柔性簇阻尼耗散的能量远远大于刚性簇阻尼耗散的能量；柔性簇阻尼能量初始增加较大，随后能量增加趋于平缓，在刚性簇中阻尼能量变化比较稳定。从阻尼耗散能量变化来看，cluster试样产生的能量比clump试样要多，说明在外力作用下，cluster试样内部颗粒所受的影响更大。

在颗粒试样中，颗粒体力定义为颗粒受重力荷载、施加的力和力矩，在加载中所产生的能量定义为体力能。两种颗粒试样体力能的变化如图9所示，在颗粒的接触模型中，选用线性接触模型，未给颗粒施加粘结，所颗粒间不存在力矩。从体力能的变化中可以看出，clump试样的体力能基本没有变化，而cluster试样的体力能逐渐减小；这说明在外力加载下，刚性簇颗粒内部的体力基本不做功，颗粒本身不发生变化，颗粒间体力基本不产生体力能；柔性簇颗粒间不产生能量，柔性簇颗粒内部发生移动、破碎，会释放能量使得颗粒自身体力能减少，这也说明外力促使柔性簇颗粒内部发生很大变化。

从上述能量的角度可以分析，颗粒破碎对试样内部能量的变化产生很大的影响，颗粒破碎促使试样动能升高、阻尼耗散的能量大大增加、颗粒内部的体力能减少，这也反映了了在外力加载下，易破碎的颗粒产生或消耗更多的能量，颗粒更容易发生运动，其内部结构变化更剧烈，试样整体稳定性变差，强度减弱。

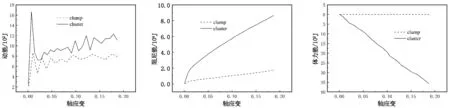
图7 不同试样动能变化 图8 不同试样阻尼耗散能量变化 图9 不同试样体力能变化

3 结论

(1)在三轴伺服压缩下，柔性簇试样颗粒发生破碎，导致颗粒剧烈移动、旋转，破碎的细颗粒填充试样内部孔隙，使得试样体积缩小更多；刚性簇试样强度较柔性簇试样强度更高，说明颗粒破碎会影响土体的受力性能，导致颗粒结构的不稳定，使得试样整体的抗剪强度有所降低。

(2)柔性簇试样由于颗粒重叠较大，且颗粒破碎后大颗粒变成小颗粒，破碎的颗粒结构发生重组，导致柔性簇颗粒配位数较刚性簇要小很多，颗粒间接触更差，使得土体结构稳定性变差。

(3)柔性簇颗粒在破碎后，生成动能更多、耗散的阻尼能更大，颗粒整体运动较颗粒不破碎时更剧烈；体力能做的功越大，颗粒簇内部做功越多，颗粒的破碎也越明显，土体结构的稳定性更容易受外力影响，这对于试样的抗剪强度有不利影响。