月面巡视机器人快速安全路径规划
于晓强,郭继峰,赵毓,颜鹏
哈尔滨工业大学 航天学院,哈尔滨 150002
在中国嫦娥四号探月工程中,玉兔二号月球车成功实现了人类首次在月背的巡视探测任务,掀开了人类探索月球的新篇章。在月球探测任务中,月球车(也称月面巡视机器人)作为任务的执行体,其能力的大小直接关乎探测任务的效率及成功性。美国阿波罗计划中的月球车已经初步具备自主能力,但还是以航天员的驾驶为主,仍处于人机配合的阶段[1]。中国玉兔二号月球车同时具备地面遥控和自主导航移动能力,其可以通过自身搭载的传感器感知周围环境并进行自主路径规划。美国正在开展高级月面巡视机器人的研究,包括全地形六角形地形探测者计划(The All-Terrain Hex-Limbed Extra-Terrestrial Explorer, ATHLETE)[2]、空间探索飞行器(Space Exploration Vehicle)[3]等,旨在开发具备高自主、全地形及大范围转移能力的巡视机器人,以支持未来月球基地的建设计划。月面巡视机器人的自主移动及探测能力无疑会给月球探测提供了更加自主鲁棒的探测模式,同时也极大提高了月球探测的效率。
在增加巡视机器人自主探测能力的同时,必须要考虑对其安全性的影响。美国“勇气号”火星车曾因车轮陷入沙地而导致无法移动,最终于2011年3月彻底失联。这说明巡视机器人的安全性是其探测任务成功与否最重要的因素,必须在自主探测过程中保证巡视机器人的安全可靠性,使其尽量远离危险区域,维持巡视机器人长期稳定的工作。
路径规划技术作为月面巡视机器人自主探测最重要的环节之一,其规划结果直接影响了探测任务的效率与安全性,受到了国内外研究人员的广泛关注。文献[4]提出一种基于地形可通过性定量评价和目标可达的局部综合避障规划方法,在实现局部避障的同时保证目标可达,并成功应用于中国“玉兔号”和“玉兔二号”月球车自主导航中。文献[5]分析了行星车自身能力约束及外部环境约束对规划的影响,并根据履带式和轮式巡视机器人不同的运动特性,对其规划路径进行了仿真,验证了其方法的有效性。
目前对于月面路径规划问题的研究大多是针对较小区域、考虑精确约束的局部避障路径规划,而随着月面探测需求以及月球车运动能力的提升,需要开展针对月面大范围移动的全局路径规划研究。全局路径规划算法主要包括启发式算法(如遗传算法、蚁群算法等)、基于采样的算法(如RRT算法、PRM算法等)以及基于图搜索的精确式算法(如Dijkstra、A*等)[6-10]。由于启发式算法及采样算法的算法机制导致求解存在较高的不确定性,不能保证解的最优性。考虑到月面探测任务的高代价及高风险性,本文主要研究具有最优性保证的精确式搜索算法。而此类算法主要的缺点是搜索速度太慢,尤其针对大范围地图中的路径搜索。
在基于图搜索的精确式算法中,如何定义代价函数(启发值函数)是路径规划的关键。即使使用相同的算法,生成的路径也可能因评估指标的不同而不同。针对月面探测路径规划的代价函数,文献[11]综合考虑了地形可达、光照情况、通信可达等多种因素,在导航单元规划中设计了考虑地形行走代价、移动里程代价、操作控制代价等因素的平滑曲线路径搜索算法。文献[5]分别考虑了距离代价、与行星车自身能力相关的地形代价、与外部环境相关的光照代价,并分析了他们之间不同权重对路径的影响。综上来看,目前代价函数的设计缺少对路径安全代价的考虑,而安全性是巡视机器人路径规划最重要的因素之一,必须保证生成的路径尽量远离危险区域,来实现巡视机器人的安全可靠探测。
本文提出了一种基于月面数字高程模型(Digital Elevation Model, DEM)地图的大范围移动快速安全路径规划算法,首先根据月面DEM地图分析地形可通过性,并生成了欧几里得距离地图(Euclidean Distance Map, EDM)。然后提出了FSA*(Fast-Safe A*)算法,改进了A*算法的搜索机制以适用于大范围的快速路径搜索,并结合EDM设计了一种安全启发式函数,极大地提高了生成路径的安全性,同时缩短了算法的搜索时间。最后以嫦娥四号着陆的南极艾特肯盆地附近区域作为仿真场景,验证了本文所提算法的有效性,并与其他主要搜索算法进行了性能对比。
1 DEM地图处理
数字高程模型是通过有限的地形高程数据实现对地面地形的数字化模拟(即地形表面形态的数字化表达)。月面DEM地图是获取月面地形信息的主要方式。目前国际上常用的月面DEM数据集包括中国嫦娥二号CE2TMap2015数据[12]、美国SLDEM数据[13]、GLD100数据[14]以及LOLA DEM数据[15]。文献[12]对他们的精度进行了分析对比,结果表明CE-2全月地形数据产品在空间分辨率、全月覆盖率、数据连续性、绝对定位精度和地貌结构细节表达等方面与其他全月地形产品相比具有明显的优势。所以本文采用嫦娥二号CE2TMap2015数据进行月面地形处理。
月球DEM数据按栅格形式存储了月面每个位置的高程信息,不能直接作为路径规划中的环境地图,需要通过提取高程数据计算深层次的地形特征信息,如坡度、平滑度等,再根据设定的巡视机器人能力限制转化为可通过性地图。
本文主要从坡度、起伏度以及粗糙度3个方面从DEM数据中提取月面地形信息,采用滚动窗口的形式计算每个栅格内的地形特征,即通过设置一个3×3栅格大小的滚动窗口,将窗口内的地形信息作为中心栅格的地形特征。
地形坡度θ由式(1)计算得到:
(1)
式中:fx为中心栅格东西方向高程变化率;fy为中心栅格南北方向高程变化率,采用三阶不带权差分方法计算:
(2)
式中:H1~H9分别为3×3窗口内部的9个栅格对应的高程值;g为DEM数据的分辨率大小。
地形起伏度R可由窗口内高程最大值与高程最小值的差计算得到:
R=Hmax-Hmin
(3)
式中:Hmax为窗口内的最大高程值;Hmin为窗口内的最小高程值。
地形粗糙度δ可由窗口内所有点的高程值标准差计算得到:
(4)

通过滚动窗口在DEM地图中依次计算,可以得到地图中所有栅格的地形信息。然后根据巡视器的能力约束,设置最大坡度、起伏度、粗糙度的阈值限制为θmax=20°,Rmax=g/2,δmax=g/5。超过此阈值限制的栅格区域视为障碍区域,据此可将DEM地图转化为规划可用的可通过性地图。
为保证探测路径的高可靠性和安全性,本文在可通过性二值地图的基础上生成了欧几里得距离地图(EDM)[16],即地图中每个栅格内储存了其距离最近障碍点的欧氏距离,并将此距离作为路径规划的启发值,保证规划出的路径尽量远离障碍区域,以提高探测任务的安全性。
选取嫦娥四号着陆点附近的南极艾特肯盆地区域作为仿真场景,采用上述方法对CE2TMap2015数据的42°S~56°S, 156°E~180°E(约540 km×440 km,50 m分辨率)区域进行地形分析处理,结果如图1所示。
由图1可以看出,本节所提出的地形计算方法可以较好地还原月面地形特征,对环形山边缘、小型山脉等危险区域有很好的提取效果。同时,EDM地图可以给出距离障碍较远的区域(图中明亮的区域),为后续安全路径规划算法提供参考。
2 大范围快速安全路径规划
由于月面探测任务的高风险性与高代价性,本节选用具有路径最优性保证的A*算法进行改进,提出了FSA*算法,首先根据大范围移动的任务场景改进了A*算法的搜索机制,加速了算法的搜索过程,然后结合EDM地图设计了一种安全启发式函数,保证生成的路径可以尽量远离障碍区域。
A*算法是一种启发式搜索算法,根据启发式函数f(n)扩展搜索的节点,f(n)=g(n)+h(n),其中g(n)为从起点到节点n的路径的确切代价,h(n)为节点n到目标点的剩余路径代价估计。文献[17]证明了当启发式函数f(n)满足一致性条件时A*可以找到最优解。同时,A*算法使用OPEN表和CLOSE表存储正在探索的节点和已经探索过的节点,首先从OPEN表中选择启发式函数f(n)最小的节点最为当前节点,并将其加入CLOSE表中,然后扩展当前节点的所有邻居节点加入OPEN表中,再选择f(n)最小的节点进行扩展,如此迭代直至搜索到目标节点。其中还要考虑当前节点的邻居节点已经在OPEN表中的情况,这时要判断由当前节点扩展的f(n)值是否更小,如果是则需要对OPEN表进行更新,并重新排序。
由此可见,A*算法在扩展的过程中,每次循环都要判断本节点是否在OPEN表和CLOSE表中,并且OPEN表内的节点可能会被探索多次,重复计算g(n)以及对OPEN表重复排序,事实上这是对路径最优性影响较小且非常耗费时间的操作,尤其是在大范围地图中搜索的情况。同时,本文所提出的安全启发式函数破坏了原启发式函数的一致性,会导致A*算法搜索失败以及进一步增加算法的搜索时间。
本节所提出的FSA*算法改变了A*算法的搜索机制,使每个节点只被探索一次,每个节点的g(n)值改为该节点与起点的对角启发式距离,是对从起点到该节点真实代价的估计值,这样做就避免了对节点的重复探索。这也导致算法不必使用CLOSE表来储存探索过的最优节点,同时,可以使用每个节点的g(n)值比较代替节点是否在OPEN表的判断以及OPEN表的排序操作,也加快了算法的搜索过程。具体算法详见算法1。
首先是对算法进行初始化(第2~6行),包括OPEN表、启发式函数f(n)、g(n)(这里将g(n)初始化为极大值矩阵)。然后是FSA*算法的扩展搜索过程(第7~22行),选择OPEN表内f(n)值最小的节点作为当前节点,对其所有邻居节点进行扩展(第13~21行),这里选择g(n)值变小的节点进行探索。g(n)值变小的节点证明是未探索过的节点,这样就避免了对节点n的多次探索以及是否在OPEN表中的判断,节省了大量搜索时间。

算法1:FSA*算法1.输入:Map, Start, Goal2.Openlist=Start∥初始化OPEN表3.f_score(start)=heuristic_safe(Start, Goal)∥初始化f(n)4.g_score = ones(length(Map),width(Map))*Inf∥初始化g(n)5.g_score(start) = 06.parent = Map∥初始化父节点查询表7.while Openlist≠NULL do8. current = the node in openlist having the lowest f_score value9. if current = goal∥到达目标节点10. return reconstruct_path(parent, current)11. end12. Openlist.Remove(current)13. for each free neighbor v of current do14. g_score_temp = diagonal_dist (start,v)15. if g_score_temp < g_score[v]16. g_score[v] = g_score_temp17. f _score[v] = g_score[v] + heuristic_safe(v, Goal)18. Openlist = [Openlist, v]19. parent(v) = current20. end21.end22.end23.return failure24.function reconstruct_path(parent, current)25. path = [current]26. while current≠Start do27. current = parent(current)28. path = [path, current]29. end30. return path
本节还定义了安全启发式函数heuristic_safe()来指导算法进行安全路径搜索:
heuristic_safe(x,y)=Diagonal_heuristic(x,y)*
(5)
式中:Diagonal_heuristic(·)为对角启发式距离函数,也可替换为欧氏距离函数或其他满足一致性条件的启发式函数;EDM(x)为第1节生成的欧几里得距离地图中节点x的距离值,表示节点x与其最近的障碍的距离值;Dismax为EDM地图中的最大距离值;α为安全系数,可以人为设定来调节算法在不同风险等级区域搜索的性能,其作用会在后续仿真验证部分详细介绍。
由于安全启发式函数引入了EDM距离,破坏了原启发式函数的一致性,同时还修改了原A*算法的搜索机制,所以不能保证FSA*算法生成的路径具有距离最优性,而本文关注的是月面巡视机器人大范围自主探测的快速安全路径规划,具体性能表现会在仿真验证部分进行详细分析。
3 仿真验证分析
3.1 仿真场景
选取嫦娥四号着陆点附近的南极艾特肯盆地区域作为大范围自主探测仿真场景,首先根据第1节所提地图处理方法生成如图1所示的可通过性地图与EDM地图,地图规模约为10 000栅格×10 000栅格。然后选取任务起点为嫦娥四号着陆点45.5°S,177.6°E,即冯卡门撞击坑中部区域,终点选取为南部的庞加莱撞击坑中上部区域55.5°S,163.9°E,因为庞加莱撞击坑是月球背面南半部一座庞大的古撞击坑,很有可能挖掘出原始月幔物质,是探测和研究深部月壳及月幔物质的理想区域,具有较高的探测价值[18]。
所有算法的仿真测试软件环境为Windows 10+MATLAB 2016,硬件环境为Intel(R) Core(TM)i5-7200U CPU+12.0 GB RAM。
3.2 有效性验证
根据3.1节设定的仿真场景,本节对FSA*算法的有效性进行验证。分别设定安全系数α=1,3,5三种情况对算法进行仿真,结果如图2所示。由图2可以看出,FSA*算法α较小的路径会更加选择图中的安全区域(较明亮区域)。

然后对不同安全系数α情况下算法的性能表现做了对比,结果如表1所示。其中,累计安全距离的定义为该路径上所有节点的累计EDM距离值,平均安全距离为累计安全距离除以路径长度,用来表征该路径的安全性。由表1可以看出,随着安全系数α的增大,FSA*算法生成的路径长度以及搜索时间逐渐变小,但路径的安全距离也随之下降,证明α可以调节算法的距离最优性和安全最优性,可以在平坦的区域增大α以增强算法的性能,而在危险的区域减小α来确保生成路径的安全性。

表1 不同安全系数情况下算法的性能对比
3.3 算法性能对比
本节将FSA*算法(α=1)与标准A*算法、MHA*算法[19]、以及JPS算法[20]进行对比,仿真条件均为3.1节所设定的仿真场景,各算法生成路径如图3所示。由图3可以看出,相比于其他算法,FSA*算法搜索出的路径会尽量选择离障碍较远的安全区域,提高了探测路径的安全性。

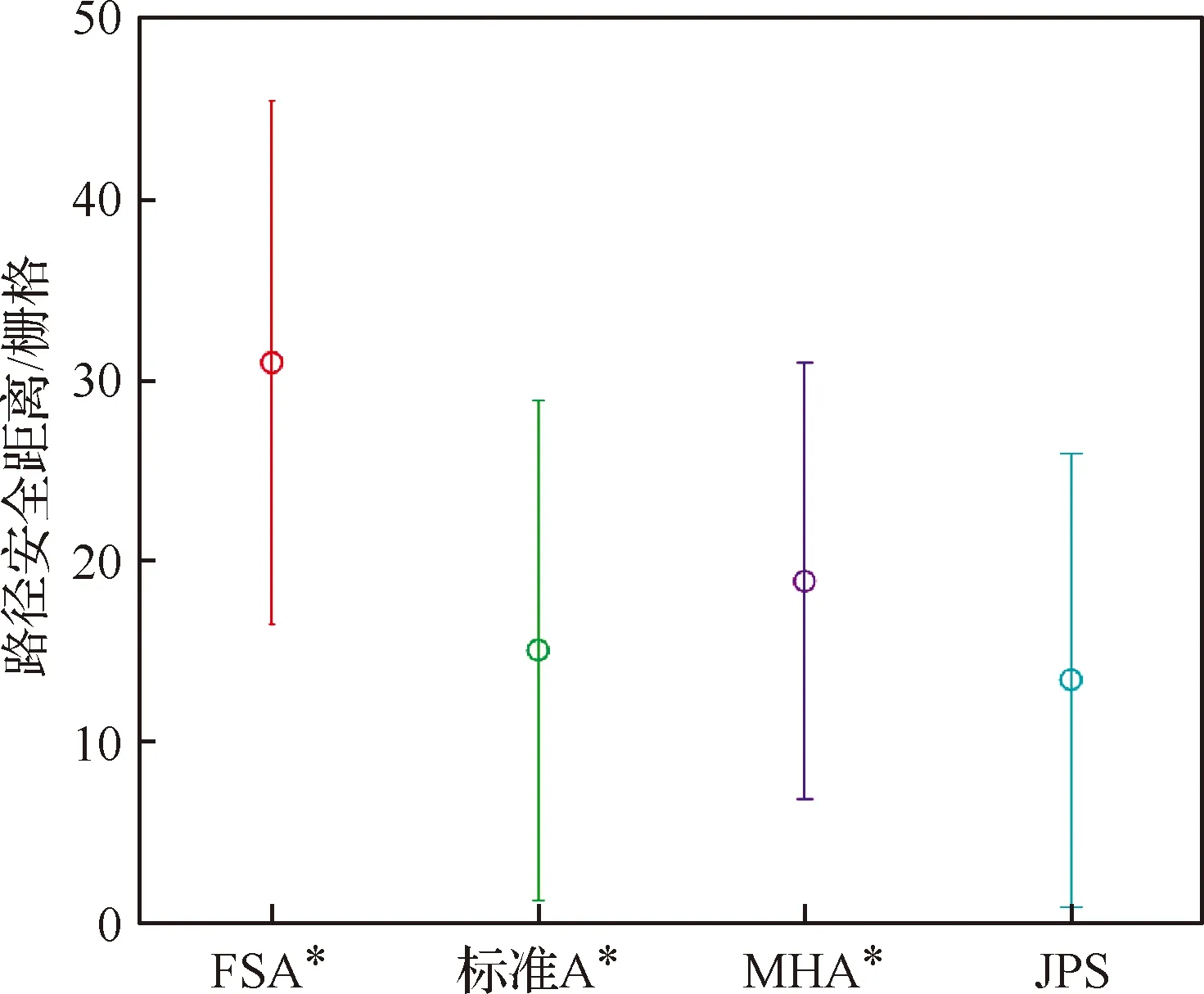
然后对这4种算法生成路径的安全距离进行了统计,结果如图4所示。可以看出FSA*算法生成路径的安全距离明显高于其他算法,可使巡视机器人在探测过程中尽量远离障碍区域,保证了自主探测过程的安全性。
然后在不同情况下对这些算法的性能表现进行统计分析,在上述场景中随机选取10组不同的起点终点位置(其中起点终点直线距离超过400 km),统计他们的性能表现,结果如表2所示。

表2 不同算法的性能对比Table 2 Performance comparison of different algorithms
由表2结果对比可以看出,FSA*算法(α=1)累计安全距离以及平均安全距离明显高于其他算法,搜索速度略低于JPS算法,高于标准A*算法及MHA*算法,说明FSA*在保证路径安全性的基础上缩短了算法的搜索时间。
4 结 论
1) 根据月面数字高程地图提出一种地形可通过性分析方法,并生成了可通过性地图和欧几里得距离地图(EDM),用于大范围安全路径规划。
2) 提出了FSA*(Fast-Safe A*)算法,改进了A*算法的搜索机制以适用于大范围地图的快速路径搜索,并结合EDM地图设计了一种安全启发式函数,可使生成路径尽量远离危险区域,提高了巡视机器人自主探测过程的安全性,同时缩短了算法的搜索时间,提高了月面大范围探测路径规划的效率与安全性。

