基于状态观测器的空间机械臂关节故障诊断
贾庆轩,符颖卓,陈钢,徐文倩
北京邮电大学 自动化学院,北京 100876
空间机械臂通常被用以协助或替代宇航员执行大量繁重复杂的在轨操作任务,如悬停飞行器捕获、载荷大范围转移、舱体组装等[1-2]。然而,受太空环境恶劣、操作任务繁重和自身结构复杂等因素的影响,空间机械臂极易发生关节故障[3]。当关节故障发生时,若不及时诊断并获得相关故障信息,不仅导致空间机械臂无法执行原定任务,且可能使得故障影响扩大,威胁机械臂的运行安全。因此,亟需开展空间机械臂关节故障诊断的研究,及时检测并诊断出故障信息,以提出相应的故障处理应对策略,保障任务的顺利进行和机械臂的安全运行。
在各类故障诊断技术中,基于解析模型的故障诊断技术是较常用的方法,其包含残差生成和诊断决策两个过程[4]。残差用来反映被诊断系统的状态,当系统无故障时,残差趋于零值,而当有故障发生时,残差偏离零值。现有研究常利用状态估计法实现残差的生成,如状态观测器方法[5]、粒子滤波器方法[6]、卡尔曼滤波器方法[7]等,其基本思想是利用实际系统的输出与观测器或滤波器的估计输出进行比较形成残差。考虑到状态观测器可以有效实时估计系统状态或输出值,本文将通过设计状态观测器跟踪空间机械臂运行轨迹,生成空间机械臂各运行状态的残差。
在状态观测器稳定跟踪空间机械臂运行轨迹后,若观测残差偏离零值,则表示发生了故障。然而,受太空中高能粒子、高层大气、航天器振动等因素的干扰[8-9],空间机械臂在轨运行时不可避免地受到外界扰动的影响,造成残差会在零值附近波动,但并不代表发生了关节故障。因此需事先为残差序列设定阈值,只有当残差超出阈值时,才可判定故障发生。当故障发生时,空间机械臂关节同时受到故障信号与外界扰动的作用,基于状态观测器的残差信息实则为两者共同作用的结果,若此时残差信息仍保持在所设定的阈值之内,则诊断系统无法给予故障的警报。针对此情况,有较多学者利用神经网络[10]、集合论[11]、特征结构配置[12]等方法对状态观测器进行干扰解耦,以消除外界扰动对残差的影响,使得残差只对故障信号敏感。然而,实际空间机械臂系统的复杂结构很难满足完全解耦的条件,且外界扰动形式多样,无法得知其变化特性,导致难以实现对外界扰动的完全解耦。借鉴文献[13]将历史数据作为衡量标准以避免误判或漏判的思想,本文利用系统大量的历史运行数据进行残差阈值的选取,若残差不超过设定的阈值,则将故障信号视为外界扰动的一种而不给出故障发生的警报,此时也不会对系统安全及任务执行效果产生影响。若故障信号与外界扰动共同作用下造成残差超出了阈值,才给予故障发生的警报。
在实现故障检测后,需对故障残差信息进行特征分析,利用合适的决策规则识别出故障模式(包括故障发生位置及故障程度),用以实现故障系统的恢复或容错控制。故障残差分析方法有神经网络法、模糊推理法、统计决策法等[14]。王建国[15]针对机器人残差信息与故障间的不确定性关系,基于模糊推理法获得系统每个运行状态的残差与不同故障模式间的隶属度,进而利用有限个运行状态的残差实现故障模式的识别。然而,空间机械臂是一个强耦合系统,任何一种故障模式的发生均会造成机械臂所有运行状态的残差发生较大的变化,此时各运行状态的残差与不同故障模式间均有可能存在较高的隶属度,若只选取有限个状态信息进行故障模式识别,容易造成其它重要信息缺失而导致故障模式的识别准确率降低。由于空间机械臂系统内部强耦合关系的存在,不同故障模式所对应的故障后系统整体运行状态存在较大的差异,考虑空间机械臂这一特点,本文通过模拟不同故障模式下机械臂运行状况,获取运动过程所有运行状态的故障残差信息,建立包含多种故障模式的故障数据库,进而采用相似度算法[16-17]判断实际故障导致的机械臂故障残差信息与故障数据库各类别间的近似程度,实现故障模式的识别。
综上所述,本文通过两个阶段开展空间机械臂关节故障诊断的研究,第一是设计状态观测器跟踪空间机械臂运行轨迹,获得机械臂各运行状态的残差信息,进而将其与设定的阈值比较,实现故障的检测并获得故障发生时刻;第二是通过在故障时刻引入不同故障模式,获得空间机械臂运行状态故障残差信息,用以构建故障数据库,进而将实际关节故障所导致的机械臂故障残差信息与故障数据库对比,识别出故障发生位置及其故障程度。本文所提空间机械臂关节故障诊断方法,可实时检测故障的发生并获得有效的故障信息,为故障系统的恢复或容错控制提供指导。
1 空间机械臂关节故障检测
检测关节故障是否发生的思路是将空间机械臂实时运行状态与期望的状态进行对比,若两者间的差异超出了阈值,则可判定发生了故障。同时,采集系统各运行状态的故障残差信息可作为识别故障模式的依据。本节在描述关节故障数学模型的基础上建立关节故障空间机械臂动力学模型,进而结合滑模变结构理论设计滑模状态观测器,通过跟踪空间机械臂运行轨迹,实现对关节故障的检测并生成故障残差信息。
1.1 关节故障空间机械臂数学模型
关节故障空间机械臂数学模型是设计状态观测器的基础。在给出关节故障数学描述的基础上,结合常态下n自由度空间机械臂动力学模型,建立关节故障空间机械臂动力学模型。
1.1.1 关节故障数学描述
按照分类方式的不同,关节故障类型可分为加性故障和乘性故障[18-19]。对于加性关节故障,其故障信号可表示为
uf=us
(1)
式中:us为关节发生加性故障后的偏移输出。
对于乘性关节故障,其故障信号可表示为
uf=(λ-I)uθ
(2)
式中:uθ为期望关节输出;λ=diag(λ1,λ2, …,λn)为关节有效输出因子矩阵,其取值范围为0≤λk≤1(k=1, 2, …,n);I为单位矩阵。
当关节同时存在加性故障与乘性故障时,关节故障信号表示为
uf=(λ-I)uθ+us
(3)
则关节的实际输出为
ua=uθ+uf=λuθ+us
(4)
1.1.2 关节故障空间机械臂动力学模型
对于n自由度自由漂浮空间机械臂,其动力学方程为[20]
(5)
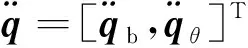
当发生关节故障时,结合关节故障模型式(3)~式(4),可得关节故障空间机械臂动力学方程为
(6)
1.2 滑模观测器结构设计
状态观测器的思想是通过构造与被控系统数学模型相似的观测器模型,将系统实际输出与观测器输出对比产生输出误差(即残差),进而反馈至观测器模型,使得正常状态下观测器残差趋于零。本节基于空间机械臂动力学模型,利用滑模变结构控制理论[21]设计滑模状态观测器,用以生成空间机械臂各运行状态的残差。
(7)
利用空间机械臂状态方程,设计滑模观测器:
(8)
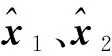

(9)
然而,符号函数极易导致观测器输出抖振[22],为消除抖振带来的高频干扰,本文采用以下双曲正切函数[23]来代替式(9)符号函数:
(10)
定义观测器残差为
(11)
将式(7)与式(8)代入式(11),可得残差方程:
(12)
选取状态观测器的滑模面为s=e1=0,根据滑模面存在条件[21]:
(13)
(14)
此时滑模观测器满足吸引性条件,即
(15)
则e2=-η2tanh(e1)-k2e1也将收敛至零,满足渐进稳定的判定条件。
1.3 故障检测及故障残差生成
当空间机械臂正常工作时,随着运行时间的增加,滑模观测器将逐渐跟踪机械臂运行轨迹,此时残差只受外界扰动的影响,其值较小,会在零值附近波动。当关节故障发生后,机械臂关节输入由uθ+ud变为λuθ+ud+us,此时式(7)的空间机械臂状态方程转化为
(16)
由式(11)可知,观测器滑模面被破坏,状态观测器将不再跟踪实际运行轨迹,即残差将不收敛于零,进而将残差与阈值相比较即可实现故障的检测。
选取系统运行状态的角度残差作为待比较的对象信息。首先选取角度残差阈值rth=(rth_1,rth_2,…,rth_n+6),其中rth_j(j=1,2,…,n+6)表示空间机械臂第j个运行状态的角度残差阈值。当无故障时,残差阈值的选择取决于系统外界扰动τd的边界,设计为
rth=f(τd)
(17)
式中:f(·)为外界扰动与残差间的函数关系,其解析式由关节故障空间机械臂数学模型确定。
残差阈值的选取依赖于设计人员的经验,选取过大时会使得系统对故障的反应迟钝,导致故障检测漏报或者延迟,选取过小又会使得系统对故障过于敏感而导致误报。为此,本文通过采集大量机械臂正常工作时的历史运行数据,确定外界随机扰动(范数有界)作用下机械臂各运行状态残差的极值,从而将该值设定为阈值。阈值选取的具体流程为
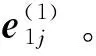
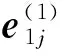


(18)

(19)
由式(7)与式(8),此时有:
f(ud+uf)>rth
(20)
式(20)物理意义即为当故障信号与外界扰动共同作用所造成的系统运行状态残差大于设定的阈值时,关节故障可被检测。
即使系统存在故障,若故障信号与外界扰动的共同作用使得残差仍保持在阈值以内,此时诊断系统依然视机械臂工作正常,而将故障信号视为扰动的一种,只表现为可能引发故障的潜在因素。当故障信号与外界扰动共同造成的残差超过阈值时,则故障可被诊断系统检测。
2 基于残差分析的关节故障模式识别
在完成故障检测并获得空间机械臂运行状态的故障残差信息后,通过分析残差特征可实现故障模式的识别。通过模拟不同故障模式下空间机械臂运行状况,采集各故障模式对应的系统运行状态故障残差信息,建立包含多类故障模式的故障数据库;利用相似度算法,判断实际故障导致的机械臂故障残差信息与故障数据库中各类别的近似程度,筛选出与实际故障残差相似度最大的一类,完成故障发生位置及故障程度的诊断。
2.1 故障数据库建立
通过在仿真平台上于故障时刻引入不同故障模式,学习各类故障模式下空间机械臂运行状态,进而采集这些运行状态数据作为故障样本,用以构建故障数据库,数学描述为
定义故障位置集为P={Jk|k=1,2,…,n},Jk表示关节编号;故障程度集为D={φl|φ=(λ,us),l=1,2,…,m},m表示故障程度总个数。取该两个集合的元素,俩俩组合构成不同的故障模式,可表示为
S={(P1,D1),(P1,D2),…,(Pi,Dj)}
(21)
式中:Pi、Dj分别表示故障位置集P的第i个元素和故障程度集D的第j个元素,则故障模式有n×m个类别。
对于故障模式(Jk,φl),由滑模观测器获得该模式下空间机械臂关节与基座的角度残差:
k_le1=[Δk_lqb,Δk_lqθ]= [Δk_lxb,Δk_lyb,
Δk_lzb,Δk_lαb,Δk_lβb,Δk_lγb, Δk_lqθ1,
Δk_lqθ2,…,Δk_lqθn]
(22)
而每个状态分量是运行时间t的函数,即在关节故障发生后在每个运行时刻ti的采样数据:
k_le1j=[k_le1j_t1,k_le1j_t2, …,k_le1j_tN]
(23)
其中i满足:
(24)
式中:tf、te分别表示故障发生时刻和仿真平台上停止数据采集的时刻;Δt表示机械臂运动规划步长;N代表故障数据库数据的长度。
通过遍历故障模式集S中的每一组元素,模拟不同模式下空间机械臂运行状况,由滑模观测器获得对应的空间机械臂状态运行状态角度残差,即可建立包含故障发生位置和故障程度信息的空间机械臂运行状态故障数据库。
2.2 基于残差相似度的故障模式识别
故障数据库包含的故障模式有多类,当实际的空间机械臂运行状态故障残差与其中某一类故障模式所对应的残差最为相似,即可识别出实际的故障模式。
设空间机械臂运行状态实际故障残差为
kd_lde1j=[kd_lde1j_t1,kd_lde1j_t2, …,kd_lde1j_tM]
(25)
式中:kd、ld表示待识别的实际故障发生位置和故障程度。残差序列维度M(即数据长度)与数据采集的时间有关。在实际工程应用中,需使机械臂在发生关节故障后继续运行一段时间,以便采集一定大小的故障信息,此时实际故障残差的数据长度M与机械臂实际运行终止时间有关,即
(26)
式中:ts为故障后空间机械臂停止运行的时刻。一般地,实际故障残差的数据长度较故障数据库的短,即M≤N。M越大,代表采集的数据所包含的故障信息越丰富,更有利于实现故障模式的识别。
式(25)所显示的残差序列是一种特殊的既有大小又有方向的高维向量,在评估其与故障数据库各故障模式间的相似程度时,需同时考虑这两方面的特点进行计算近似度。为此,利用向量夹角的余弦值和欧式距离来评估实际故障残差与故障数据库各故障模式间的相似度,实现kd、ld的识别。
余弦相似度表征了对象在方向上的相似度,对于向量a、b,定义其间的余弦相似度为[16]
(27)
欧式距离相似度表征了对象在绝对数值上的相似度,定义其间的欧式距离相似度为[17]

(28)
dist(a,b)的值越小,表示a、b的相似度越高。
由于机械臂各运行状态的残差具有不同数量级的大小,需对数据进行归一化处理以便在同一数量级下分析残差特征。对于序列k_le1j、kd_lde1j,按式(29)进行归一化:
(29)
利用归一化处理后的残差信息,基于余弦相似度和欧式距离相似度,定义实际故障残差与故障数据库各类故障模式间的相似度为
(30)

式(30)是基于机械臂所有运行状态的角度残差所构建的相似度指标,由此即可获得维度为n×m的相似度矩阵Φ。通过寻找相似度矩阵Φ中最大的元素,将对应的行列序号k与l作为实际故障发生的位置和故障程度信息,完成故障模式的识别。
3 仿真研究
以7自由度空间机械臂为研究对象,验证基于状态观测器的空间机械臂关节故障诊断方法。7自由度空间机械臂结构如图1所示,其D-H参数和动力学参数分别如表1和表2所示。实验仿真中,机械臂运动规划步长为Δt=0.05 s。

图1 7自由度空间机械臂结构Fig.1 Structure of 7-DOF space manipulator

表1 空间机械臂D-H参数Table 1 D-H parameters of space manipulator

表2 空间机械臂动力学参数Table 2 Dynamics parameters of space manipulator
3.1 关节故障检测及故障残差生成
利用随机数法在0~1之间产生随机值作为随机变量,设外界随机扰动力矩为
τd=(-1.5+3rand(·))sin(rand(·)Δt)
(31)
式中:rand(·)表示在[0,1)范围内取值的随机函数。
根据观测器的收敛条件,可令所设计的滑模观测器增益矩阵为
(32)
设空间机械臂初始状态为[0 m, 0 m, 0 m, 0°, 0°, 0°, -50°, -170°, 150°, -60°, 130°, 170°, 0°],而滑模观测器初始观测值为[0 m, 0 m, 0 m, 0°, 0°, 0°, -45°, -165°, 155°, -55°, 15°, 175°, 5°],利用滑模观测器跟踪空间机械臂运行轨迹。仿真结果如图2所示。

图2 基于滑模观测器的空间机械臂轨迹跟踪Fig.2 Trajectory tracking of space manipulator based on sliding-mode observer
从图2可以看出,空间机械臂开始运行时,由于机械臂初始状态与观测器初始观测值不一致,两者的轨迹不重合,但随着运行时间的增加,观测器逐渐跟踪上空间机械臂运行轨迹,残差逐渐趋于零,结果如图3所示。
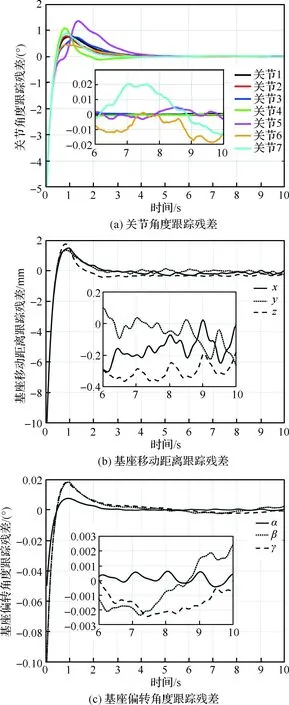
图3 空间机械臂正常运行时滑模观测器观测残差Fig.3 Residuals of sliding-mode observer with manipulator being at normal state
从图3可以看出,约从6 s开始,空间机械臂各状态故障残差二范数的数量级保持在10-2(单位:m或(°)),表明此时状态观测器已稳定跟踪空间机械臂运行轨迹。
通过多次模拟仿真空间机械臂正常运行状况,可以获得观测器稳定跟踪空间机械臂运行轨迹后(6 s后)各状态观测残差信息。设置仿真实验次数为K=50,依据式(18)选取故障残差阈值为:
rth=[0.014 0 m, 0.011 4 m, 0.013 9 m, 0.000 2°,
0.002 2°, 0.002 1°, 0.003 9°, 0.001 1°,
0.006 0°, 0.006 4°, 0.027 6°, 0.046 0°,
0.040 2°]
(33)
假设在8 s时空间机械臂关节2发生故障,不考虑发生加性故障的情况,设其故障程度为φ=[0.003,0]。则空间机械臂各运行状态故障残差如图4所示。

图4 关节2故障时滑模观测器残差Fig.4 Residuals of sliding-mode observer with failure occurring at joint 2
从图4可以看出,在8 s之前,基于滑模观测器的空间机械臂轨迹跟踪曲线与图2基本一致。而从8 s开始,随着时间的积累,空间机械臂实际运行轨迹逐渐偏离观测器所观测的轨迹,各运行状态的残差不再收敛。在8.15 s时,有
(34)
关节1与关节2的角度残差超出了设定的阈值,表明空间机械臂在8.15 s发生了关节故障。所检测的故障发生时刻与实验所设置的故障时刻大体一致,说明故障检测方法是有效的。然而,此时仍无法识别故障位置及故障程度。3.2节可通过在8.15 s引入不同故障程度的不同关节故障,构建对应的空间机械臂运行状态故障数据库,基于此实现故障模式识别。
3.2 关节故障模式识别
当关节3在8.15 s发生故障时,空间机械臂运行状态的故障残差如图5所示。与图4对比,关节故障后的机械臂各状态有很大的差异,说明不同故障模式所造成的机械臂运行状态是不同的。从这个角度出发,若能够建立包含不同故障模式对应的空间机械臂运行状态故障数据库,则当实际发生某种故障时,将实际故障数据与故障数据库对比,即可识别故障发生位置与故障程度。

图5 关节3故障时滑模观测器残差Fig.5 Residuals of sliding-mode observer with failure occurring at joint 3
不考虑发生加性故障的情况,即故障程度的偏移分量us为零,选取发生乘性故障的有效因子λ范围为[0.001,0.005],在建立故障数据库时,设置故障程度有[0.001,0],[0.002,0],[0.003,0], [0.004,0],[0.005,0]5种可能。而故障关节发生位置均有可能发生在各关节上,即有7种可能,因此故障数据库的故障模式有35(=5×7)类,且故障数据库每一类模式下由13(=6+7)个运行状态的残差组成。取故障残差库的数据长度为
考虑外界扰动的影响,在构建故障数据库每类故障模式对应的运行状态残差时,设置模拟实验次数为100次,然后在每个时刻取100次模拟实验的各运行状态故障残差的平均值,作为对应运行状态最终的故障残差,进而通过遍历各类故障模式,完成故障数据库的建立。
设3.1节中空间机械臂在关节2发生故障后1 s停止运动,则采集的实际故障残差的数据长度为
令权值系数ρ=0.8,将长度为20的实际故障残差与故障数据库对比,根据式(30)求解其间的相似度矩阵为
Φ=

(35)
矩阵Φ中,第2行第3列的元素值最大,说明与故障数据库中关节2发生故障程度为[0.003,0]的这一故障模式最为相似,同本文仿真实验的初始设置一致,验证了本文所提诊断算法的正确性。
根据式(30),不同的权值系数ρ将会影响实际故障残差与故障数据库各类故障模式间的相似度,从而影响诊断的结果。为探究故障诊断正确率与所选的ρ间的关系,计算不同的权值系数ρ∈[0,1]下相似度矩阵。设置每个不同的ρ对应的实验次数为50次,实验结果如图6所示。

图6 故障诊断正确率与权值系数ρ间的关系Fig.6 Relationship between accuracy of fault diagnosis and weight coefficient ρ
结合图6与式(30)可以看出,当侧重于使用余弦相似度进行故障诊断时,诊断正确率比较高;当侧重于使用欧式距离相似度进行故障诊断时,则诊断正确率比较低。
仿真实验在建立故障数据库时只考虑了乘性故障,但并不影响故障诊断方法的有效性,即实际应用过程可以利用本文方法建立同时考虑乘性故障和加性故障的故障数据库,以实现相关故障信息的诊断。
4 结 论
1) 在建立关节故障空间机械臂数学模型的基础上,设计状态滑模观测器实现对空间机械臂运行轨迹的跟踪,以获得系统各运行状态的残差信息。
2) 通过多次模拟空间机械臂正常工作状况选取残差阈值,进而比较系统运行状态残差与阈值,实现了关节故障的检测。
3) 通过在故障时刻引入不同故障模式,构建故障数据库,并将实际关节故障残差与故障数据库进行对比,实现了故障发生位置及其故障程度的识别,完成空间机械臂关节故障诊断。

