空间多机器人协同的多视线仅测角相对导航
韩飞,刘付成,王兆龙,杜宣,刘珊珊,刘超镇
1. 上海航天控制技术研究所,上海 201109 2. 上海市空间智能控制技术重点实验室,上海 201109 3. 上海航天技术研究院,上海 201109
近年来,随着空间碎片环境的急剧恶化[1-2],面向主动碎片清除、在轨服务等任务的空间机器人[3]成为国际上的研究热点。多个微纳型空间机器人相互协同,能够灵活实现大型碎片的自主逼近捕获,具备研制周期短、清除成本低等优势,相比大卫星,更适合数量巨大、轨道分散的失效卫星等大型碎片清除任务。
自主相对导航是空间碎片逼近捕获的前提。考察当前可用的典型空间碎片远程相对导航敏感器,如表1所示。其中,激光雷达、微波雷达可以通过主动测量获得目标的相对距离和视线方向信息,重量、功耗与量程直接相关;可见光/红外相机则只能通过被动测量获得视线方向信息,但是具备重量轻、功耗低的明显优势。
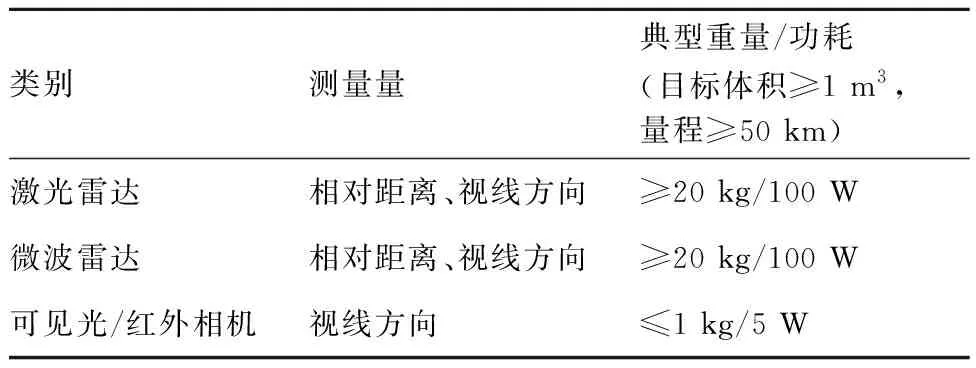
表1 典型空间碎片远程相对导航敏感器
由于微纳空间机器人承载能力有限,无法安装远程主动测量设备,不具备远程测距能力,如何仅利用光学相机测得的视线角信息实现目标准确定位,是决定自主交会和后续任务能力的关键问题,受到广泛关注。
Geller等[4-5]先后证明了单个空间机器人对非合作目标仅测角导航的可观性,并提出了可观性判据。欧空局PRISMA计划在2011和2012年先后开展两次飞行试验,初步验证了仅测角导航的可行性[6]。德国宇航中心主导完成了AVANTI任务,进一步验证了在轨自主状态下的仅测角相对导航技术[7]。但是,由于观测量中距离信息的缺失,仅测角导航系统中相对距离状态的可观测度严重下降,估计误差较大,甚至容易出现滤波发散的情况。
国内外学者针对该问题开展了大量研究,提出的方法可以概括为4类:机动法、相机偏置法、复杂动力学法和多视线协同法。
在空间机器人对非合作目标的轨道交会过程中,通过增加或优化轨道机动路径可以改善状态的可观测性[8-10],但是机动路径规划往往面临任务约束与可观测性之间的矛盾。通过偏置安装相机,可以在距离较近时获得较好的距离可观测度,文献[11-13]分别提出了相机偏置安装的方案,并推导了可观测度与偏置安装参数之间的关系,但是这种方式只适用于较近距离,不适用于更为关键的远距离情况。通过引入J2地球非球形摄动、大气阻力摄动等因素,构建非线性相对动力学模型,理论上可以使线性模型中不完全可观的距离状态完全可观,Gaias等[14]提出了基于相对轨道根数的非线性动力学模型,本文作者[15]建立了球坐标系下的非线性状态方程和线性观测方程,使视线角直接成为系统状态量,加强测量量对动力学预测的修正效果,进而采用无迹滤波(UKF)算法,提升了目标未知机动下的仅测角导航性能;多种考虑引力高阶项和摄动的动力学模型被应用到仅测角导航中[16-17],Li等[18]应用平方根无迹滤波(SRUKF)算法提升了仅测角相对导航性能,但是,复杂动力学模型求解困难,且收敛慢、受滤波器参数影响明显,实际性能提升并不明显。
通过2个及以上空间机器人,同时测量同一目标的视线方向,融合双或多视线角信息,可以使得系统状态完全可观,从而大幅提升估计性能[19-23]。李松等[19]提出了导弹集群对同一目标多视线协同仅测角相对定位方法,但是并不适用于空间机器人的动力学环境。高学海等[20]针对高轨非合作目标,提出了基于双空间机器人的多视线分布式相对导航方法,并设计了分布式求解策略;王楷[21-22]和陈统[23]等提出了双视线相对导航的方法和模型,为避免双追踪航天器和目标视线共线,提出了编队构型设计方法,但是编队构型局限在中心星加一颗伴星的形式,未考虑双伴星、多伴星下的可观度与构型优化问题,且构型优化仅考虑避免双视线共线,优化因素和方法并不明确。
上述研究均充分证明了多视线协同可显著提高仅测角导航的可观测度,但是仍有大量新的问题等待研究解决。一方面,大部分为中心机器人加一个伴飞机器人的模式,对于多伴飞机器人多视线协同模式研究较少;另一方面,均未深入研究多视线融合策略、多机器人相对运动构型等因素对可观测度的影响。
为通过空间多机器人的多视线协同提升仅测角导航估计性能,本文首先构建了一种多伴飞机器人的多视线协同仅测角相对导航系统,基于二阶CW方程构建了中心机器人与目标间的相对动力学模型和状态方程;考虑仅由伴飞机器人测量目标视线角,构建了适应视线数量可变的观测方程,结合扩展卡尔曼滤波(EKF)算法,形成了多视线仅测角导航方法;然后通过系统矢量几何关系,分析了系统的可观测性,并得出了系统可观度最优的视线间夹角条件;基于该条件,结合空间相对运动的J2能量匹配条件,给出了兼顾可观测度和长期自然维持的多伴飞机器人构型优化规则;最后,典型场景下的数学仿真结果表明,本文提出的多视线仅测角导航方法、可观度优化条件和观测构型优化规则,能够显著提高距离状态的可观测度和估计精度。
1 多视线仅测角相对导航系统
传统的双视线仅测角相对导航,一般采用一个中心机器人和一个伴飞机器人的模式,两者同时测量同一目标视线角,中心机器人同时测量伴飞机器人相对位置,最终由中心机器人完成测量量采集和滤波估计。
与双视线系统不同,本文首先构建一种多空间机器人多视线协同的仅测角相对导航系统:多个伴飞机器人对一个中心机器人稳定绕飞,并测量同一目标的视线角;中心机器人并不直接测量目标视线角,通过差分GNSS相对导航获得每个伴飞机器人的高精度相对位置,并采集伴飞机器人测量得到的目标视线角信息,通过滤波估计,得到目标相对于自身的相对位置与速度。2个伴飞机器人系统主要坐标系与矢量关系如图1所示。Op-xpypzp、Oc1-xc1yc1zc1、Oc2-xc2yc2zc2、Ot-xtytzt分别为中心机器人、伴飞机器人c1、伴飞机器人c2和目标碎片的第二轨道坐标系;ρ1、ρ2、ρpt分别为伴飞机器人c1、伴飞机器人c2、中心机器人与目标间相对矢量,d1、d2分别为对应单位矢量方向;ρp1、ρp2分别为伴飞机器人c1、伴飞机器人c2与中心机器人间的相对矢量;(α1,β1)、(α2,β2)分别为伴飞机器人、伴飞机器人测量得到的目标视线角。

考察如上几何关系,每个伴飞机器人ci都可以获得目标T相对自身的视线角(αi,βi)(i为伴飞机器人编号),具体定义:
αi为目标视线方向在ci轨道坐标系中的高低角,定义为目标相对视线方向矢量与其在轨道平面(XOZ平面)内投影之间的夹角;βi为目标视线方向在轨道坐标系中的方位角,定义为目标相对视线方向在轨道平面(XOZ平面)的投影与X轴正向之间的夹角。

1.1 系统状态方程

(1)
式中:ωip为中心机器人的轨道角速度大小;ap为中心机器人的轨道半长轴,中心机器人三轴控制加速度矢量Up=[upx,upy,upz]T。
进一步将式(1)写成状态方程形式:
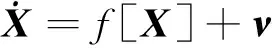
(2)
f[X]=
(3)
式中:v为模型误差向量。
上述模型为非线性模型,为适应滤波算法,需要首先对其进行离散化和线性化处理。运用成熟的方法,以采样时间T对模型离散化,得到
Xk+1=Xk+f(Xk)T+νk
(4)
式中:Xk+1、Xk、νk分别为k+1和k时刻的状态量和模型误差。
定义

(5)
(6)

(7)
式(6)可化为
(8)
式(8)中括号项可定义为外加控制项Uk,即
(9)
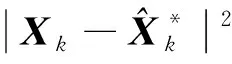
中心机器人自身控制加速度可由加速度计实时测量,将其加入动力学方程中,即
Uk=FUp(k)T
(10)
式中:F=-[03×3,I3×3]T;Up(k)为实时测量得到的控制加速度,Up(k)=[upx(k),upy(k),upz(k)]T。
这样,式(8)就可以表示为如下卡尔曼滤波方程中的动力学模型:
Xk+1=ΦXk+Uk+νk
(11)
1.2 系统观测方程
系统观测量为伴飞机器人测量得到的各自轨道系下目标视线角(αi,βi)。目标在伴飞机器人ci轨道系下的相对状态定义为Xi=[xi,yi,zi,

(12)
由矢量关系不难得到ρi=ρpt-ρpi。考虑伴飞机器人和中心机器人轨道坐标系近似平行,忽略ρpt等矢量在2个坐标系下的坐标偏差,可知
(13)
伴飞机器人和中心机器人之间通过差分GNSS确定相对位置,因此矢量ρpi可作为带有误差的已知量,现有技术能够达到较高的精度(数米到数十米)。观测量(αi,βi)的测量误差除跟瞄设备自身测量的误差之外,还包含了跟瞄设备的安装误差和伴飞机器人姿态确定误差。
采用上述观测量的观测模型为
Z(t)=[α1,β1,α2,β2,…,…,αN,βN]T=
h(X)+ψ
(14)
(15)
式中:Z(t)为实测值;h(X)为计算值;ψ为测量误差;N为纳入视线角测量的伴飞机器人个数。
对其进行离散化和线性化处理,得到适用于卡尔曼滤波算法的观测方程为
Hk+1Xk+1+ψk+1
(16)
式中:
(17)

(18)
1.3 滤波算法
本文采用如下扩展卡尔曼滤波(EKF)算法进行滤波求解。
(19)
(20)
Kk+1=Pk+1,kH(Xk+1,k)T[H(Xk+1,k)Pk+1,k·
H(Xk+1,k)T+Rk+1]-1
(21)
(22)
Pk+1=(I-Kk+1H(Xk+1,k))Pk+1,k
(23)
式中:Qk为系统模型噪声协方差阵;Rk为测量噪声协方差阵;Pk为状态转移协方差阵。与常规EKF不同之处在于,状态一步预测值是对状态方程进行数值积分求解得到的,数值积分算法采用四阶龙格-库塔方法。
2 考虑可观测度的观测构型优化
2.1 可观测度分析

进一步,根据正弦定理,可以获得目标相对于伴飞机器人的相对距离为
(24)
式中:θ1t为矢量ρ21与ρ2的方向夹角;θ12为矢量ρ1与ρ2的方向夹角。ρ1与ρ2单位矢量方向d1和d2均可由伴飞机器人测量得到的视线角求解得到
(25)

式中:Apoi、Ai1o、Ai2o分别为中心机器人和2个伴飞机器人自身轨道系与惯性系间转换矩阵,可以由各自轨道数据计算得到。

可见,上述测量量实际上已经对中心机器人与目标之间的相对位置矢量构成了完整约束,因此能够保证系统状态完全可观。
(26)

2.2 多视线观测构型优化
根据前述分析,为提高多视线仅测角导航系统的可观测度,需要使视线夹角尽量接近90°,可依此设计伴飞机器人相对中心机器人的伴飞构型。同时,考虑到微纳机器人轨道控制能力受限,构型设计还需考虑在尽量长的时间内自然保持对中心机器人的稳定伴飞,且避免碰撞。为此,文献[24]提出的基于J2能量匹配的星群构型设计方法,结合可观测度,优化伴飞构型。
综合增大视线夹角和长期自然维持两方面需求,提出机器人集群伴飞构型的设计规则:
1) 成对布置,任意时刻每一对伴飞机器人对中心机器人对称分布。
2) 各伴飞机器人相对中心机器人的绕飞轨迹为封闭椭圆,且与中心机器人轨道系YOZ面的交点分布在一个半径为Rop的交点圆上。
3) 以交点圆上的交点作为伴飞机器人相对于中心机器人的初始相对位置,基于文献[24]中提出的J2能量匹配条件,计算得到初始相对速度,如此构成初始相对运动状态,进而在无控下形成相对运动轨迹,作为期望运动构型。
按照上述原则,通过设计Rop大小和交点数量与相位分布,即可确定伴飞空间机器人相对中心机器人的绕飞构型。
以6个伴飞机器人为例,符合上述构型设计规则的机器人间几何关系如图3所示。

当目标位于中心机器人同轨道前方或后方时,Rop大小决定了相位对称伴飞机器人过交点圆时对应的视线夹角θij大小,且满足:
Rop≈ρpttan(θij/2)
(27)
因此,在目标距离粗略已知时,可根据期望的视线夹角,设计交点圆半径Rop。
除了通过构型设计优化视线夹角,还需要考虑相对运动导致的视线夹角随时间的变化,将在后面通过数学仿真进一步说明。
2.3 导航估计性能评估
Fisher信息矩阵(Fisher Information Matrix, FIM)和克拉美劳下界可以作为状态估计性能的评估工具[25],也可用来定量描述和对比系统状态可观测度。
对于观测与导航步长确定,且无轨道机动时,FIM阵的离散递归公式为
(28)
(29)
k时刻的克拉美劳下界由对应FIM阵求解
(30)
该下界表征了对应时刻导航估计的均方差下限,其值越小,则导航估计能够达到越高的精度。
3 数学仿真分析
3.1 伴飞机器人集群观测构型设计
不失一般性,假设目标和中心机器人的初始轨道根数如表2,中心机器人初始位于目标同轨道后方约50 km处。
假设伴飞机器人数量6颗,设定交点圆半径Rop=5 km,各伴飞机器人对应交点相位均匀分布,按照上述规则设计得到的伴飞机器人集群相对于中心机器人的绕飞构型、相对于目标的运动轨迹分别如图4和图5所示。

表2 目标和中心机器人的初始轨道根数Table 2 Orbital elements of two satellites at initial time


可见,三对相位对称伴飞机器人相对于中心机器人形成3条空间椭圆绕飞轨迹,且在无控的3个轨道周期内的漂移量极小,满足长期自然维持要求;各伴飞机器人相对于目标运动轨迹则存在明显漂移,主要是由于耦合了中心机器人相对于目标的漂移运动。
考察图6所示的多机器人于目标间视线夹角的变化曲线,分别对应伴飞机器人sat6与中心机器人视线夹角(sitap6),以及sat1与sat4、sat2与sat5、sat3与sat6三对相位对称伴飞机器人的视线夹角(sita14、sita25、sita36),均呈现周期变化。

伴飞机器人经过交点圆时,相应对称伴飞机器人之间的视线夹角大小约为11.4°,是伴飞机器人与中心机器人之间视线夹角的2倍。基于前面分析,采用相位对称伴飞机器人的视线角测量量,理论上能够获得更优的仅测角相对导航性能。
3.2 多视线仅测角相对导航数学仿真分析
3.2.1 仿真参数
仿真步长为0.4 s;仿真时长为18 000 s(约3个轨道周期);跟瞄设备测量精度:高低角和方位角均为0.05°(3σ)。按照前面设计的6机器人伴飞构型,结合中心机器人初始轨道根数,解算得到每颗伴飞机器人的初始轨道。设定滤波初值的相对位置误差三轴均为300 m(3σ),相对速度误差三轴均为0.3 m/s(3σ)。
3.2.2 仿真结果
1) 双视线仅测角导航
在相同场景下,分别对单视线模式、中心机器人加一个伴飞机器人的传统模式、相位对称双伴飞机器人模式,进行100次蒙特卡罗数学仿真,经过统计分析,对比导航精度、克拉美劳下界。
传统模式选择sat6的视线角测量量,双伴飞机器人模式选择相位对称的sat2和sat5视线角测量量。仿真得到3种模式对应的相对位置误差曲线分别如图7~图9所示。图中蓝色实线为各状态估计误差均值,红色点线为各状态估计误差统计分布范围(3σ),紫红色点虚线为各状态估计误差对应的克拉美劳下界。



可见,相对于单视线仅测角导航,中心机器人加一个伴飞机器人的双视线仅测角导航在距离方向(X轴)导航精度从650.72 m大幅提升到83.94 m,说明系统具备较好的可观测度;本文提出的相位对称双伴飞机器人模式的X轴导航精度进一步改善到43.10 m,说明通过本文提出的伴飞构型优化方法,增大了两颗观测机器人之间的视线夹角,从而提升了系统可观测度,证明了可观度分析结论和构型优化方法的有效性。
2) 四视线仅测角导航
联合考察图6和图9,图9中X轴误差显示,系统可观测度和导航噪声呈现周期变化,且周期特性与图6中sat25视线夹角周期特性一致,说明主要是由于双伴飞机器人视线夹角大小直接影响导航精度。为此,考虑进一步增加周期特性相互补偿的视线角测量量,从而获得全时段更优的视线夹角分布。
根据视线夹角大小,选择sat2和sat5、sat3和sat6两对对称伴飞机器人,同时设定相互相位差为0.25轨道周期,以保证综合视线夹角最优。这一设定可以通过伴飞轨迹控制实现。其他仿真参数与前面相同,进行100次蒙特卡罗数学仿真,经过统计分析,获得四视线仅测角导航的位置误差曲线如图10所示。

可见,通过增加视线角测量量,并优化视线夹角分布,距离方向X轴相对位置导航精度进一步提高到31.19 m,且导航噪声和系统可观测度的周期变化基本消失,说明稳定性明显提升。汇总各种模式下的相对导航精度如表3所示。

表3 相对导航误差Table 3 Relative navigation errors
4 结 论
本文研究了空间多机器人协同的多视线仅测角相对导航问题。构建了仅由多伴飞机器人测量视线角的多视线仅测角相对导航系统;分析了可观测度最优的视线间夹角条件,提出了兼顾可观测度和长期维持的多伴飞机器人观测构型优化规则,数学仿真证明了观测构型优化后多视线仅测角相对导航性能的显著提升,主要结论如下:
1) 多视线仅测角相对导航系统状态是完全可观的,且距离状态的可观测度与视线间夹角相关,接近90°时能够达到最优可观测度。
2) 由相对对称的两个伴飞机器人进行视线测量,能够比中心机器人加伴飞机器人的传统模式获得更接近90°的视线夹角,使得距离状态可观度更优。
3) 通过优化设计2对伴飞机器人的绕飞构型,相互补偿视线夹角的周期变化,可以明显提升导航精度和系统可观测度的稳定性。
4) 通过优化多个伴飞机器人相对中心机器人的绕飞构型,可以在增大视线夹角,改善距离状态可观度的同时,满足长期自然维持需求,具有较强的应用价值。
综上,本文提出了多视线仅测角相对导航系统、可观测度最优条件、观测构型优化方法,能够有效提升多视线仅测角相对导航系统性能,可为通过多视线融合提升仅测角相对导航性能提供有效途径,对于空间多机器人协同下的大型碎片自主交会等任务具有较好的参考和应用价值。

