基于多智能体强化学习的空间机械臂轨迹规划
赵毓,管公顺,郭继峰,于晓强,颜鹏
哈尔滨工业大学 航天学院,哈尔滨 150001
近年来,人类对太空探索和开发活动愈发频繁,对空间机械臂的能力提出了更高要求[1]。空间飞行器在轨运行过程中,易发生空间碎片近距离碰撞或表面结构脱离等突发情况,可以通过空间机械臂的有效抓捕动作使得飞行器避免主体结构受到损坏[2]。受限于任务场景的动态性和偶发性,传统空间机械臂轨迹规划方法难以满足实时性需求,为了保证能够高效完成相关动作,亟需开展空间机械臂快速自主在轨捕捉操作的轨迹规划算法研究[3]。
本文研究的空间自由漂浮机械臂系统轨迹规划问题与地面机械臂相比,有很大不同:① 空间机器人基座不固定,系统存在非完整约束,无法使用地面机械臂路径规划方法求解;② 空间机械臂Jacobi矩阵受载具平台动力学影响,其动力学奇异比地面机械臂复杂很多;③ 当前通讯条件下很难实现对空间机械臂的地面实时遥操作,因此对其轨迹规划自主性要求远高于地面系统。
空间机械臂轨迹规划目的是,在动力学和运动学约束条件下设计一条以时间为参数的连续曲线,使机械臂末端执行机构在一定时间内达到特定姿态和位置[4]。考虑到空间机械臂在运动过程中会对基座状态产生扰动,其轨迹规划问题需要在动量守恒前提下求解,整个系统存在非完整性约束[5]。针对以上特性,传统方法采用Jacobi矩阵和Lyapunov函数等算法进行系统动力学耦合分析,并以此为基础进行轨迹规划。Yoshida等采用广义Jacobi逆矩阵方式求取可执行轨迹[6]。徐文福采用求解参数方程方法进行轨迹规划,其中将关节角函数进行参数分解,然后通过牛顿迭代法取得最优解[7]。崔浩和戈新生使用多项式插值结合序列二次规划方法改进了参数方程求解算法[8]。刘宏等应用控制理论,基于Lyapunov函数对机械臂轨迹进行设计,该方法充分考虑了空间机械臂非完整约束特点[9]。随着群体智能算法兴起,王明等提出了基于群智能粒子群算法的机械臂轨迹规划方法,并以此实现了最小扰动规划轨迹[10]。上述基于数值求解和优化的空间机械臂轨迹规划算法虽然能够得到较为准确和理想的结果,但始终限制于计算量庞大和局部最优难以跳出的困境,无法应用在实时捕捉系统中。
随后机械臂运动规划算法逐渐向全局规划方向发展,常见机械臂全局轨迹规划方法包括人工势场法[11]、随机采样法[12]和智能优化方法[13]。早期有学者提出适用于不确定动态环境的基于随机采样机械臂运动规划算法,研究主要围绕快速扩展随机树(Rapidly-exploring Random Trees, RRT)方法开展[14-15]。基于RRT的算法虽然在一定程度上解决了奇点问题和不确定环境问题,但运算效率仍然是其瓶颈。本文采用文献[16]中改进RRT算法作为对比方法,应用在所研究场景中。
伴随人工智能技术研究的热潮[17-18],以强化学习[19-20]和深度学习[21-22]为代表的自学习算法被广泛应用于机械臂运动规划工程问题中。基于机器学习算法进行空间机械臂轨迹规划的优点为其适用性较强,对非完整约束可以进行有效求解,也可以在无模型的条件下进行训练仿真,甚至可以实现规划行为的预测和提前分解。2017年OpenAI研究组发表了一种基于多智能体的Actor-Critic研究方法,该方法用于训练智能体在特定环境中进行协同决策[23]。本文提出的自学习训练方法灵感即来源于此文,空间机械臂系统可以视为由多个独立的机械刚体关节杆件组成,其中每个关节杆件都可以看成一个智能体。由此,空间机械臂对运动目标捕捉的规划问题,可以看作是多个智能体连续动作协同决策问题。
本文针对某型六自由度空间机械臂建立了多关节杆件的标准DH(Denavit-Hartenberg)参数模型。对空间机械臂系统的一般运动方程进行研究,引入多刚体力学耦合特性分析,进一步推导出机械臂与基座的组合体运动学与动力学模型。结合多智能体深度确定性策略梯度学习理论,建立空间机械臂对匀速直线运动目标捕捉的强化学习训练系统。通过集中训练与分布式执行方式,对捕捉问题进行智能化自主轨迹规划。将每个机械臂关节视为一个决策智能体,训练过程中使用观察全局的Critic指导训练,进而实现多智能体的协作行为,提升强化学习稳定性。使用深度强化学习方法进行空间机械臂轨迹规划的优点在于:避免了复杂系统无法精确建模问题;解决了陷入局部最优解问题;有效降低了实时计算复杂度,提高规划效率;实现了在线自主轨迹规划。
本文所述方法是一种即时决策方法,可以进行快速连续决策,不像传统控制方法需要对控制律进行求解。随着“数字孪生”等技术的发展,通过计算机仿真模拟即可实现规划决策神经网络训练,离线训练好的规划系统移植到实物系统中经过少量在线训练就能够达到应用要求。国内很多机构已经实现了地面模拟空间机械臂的实物实验系统,可以进行地面模拟训练[24]。基于以上分析,如果未来有应用需求,本文算法可应用于实物验证和使用环境。
本文所述自学习训练方法采用Python的TensorFlow工具包进行开发,为了直观展示所得仿真结果,使用MATLAB的Robotics工具箱进行验证和绘图。用于对比分析的改进型RRT算法在MATLAB环境下实现。将两种方法的仿真结果进行对比分析,可得本文提出的算法得到轨迹规划时间更短,所得轨迹平滑度更高,对环境参数不确定情况具有较好的鲁棒性。
1 问题描述与系统建模
1.1 空间捕捉问题简化
本文研究对象为在轨运行的自由漂浮小型六自由度机械臂系统,机械臂基座安装在自由漂浮平台一端,展开结构如图1所示。由于空间环境特殊性,仅通过仿真分析验证算法,并未进行实物实验。
为了关注轨迹规划问题本身,对研究环境进行如下假设:
1) 将目标物体理想化为均质小球,球体在机械臂近距离空间内做匀速直线运动,仿真初始时刻一定时间内不会飞出机械臂工作空间。
2) 不考虑末端执行机构对小球的抓捕动作,为机械臂末端位置与球体质心位置重合即为捕捉成功。
3) 将机械臂基座平台抽象为零控均质刚体,在目标捕捉过程中忽略平台-机械臂系统整体受到的一切外力和外力矩。
仿真所用机械臂对象的DH参数如表1所示。
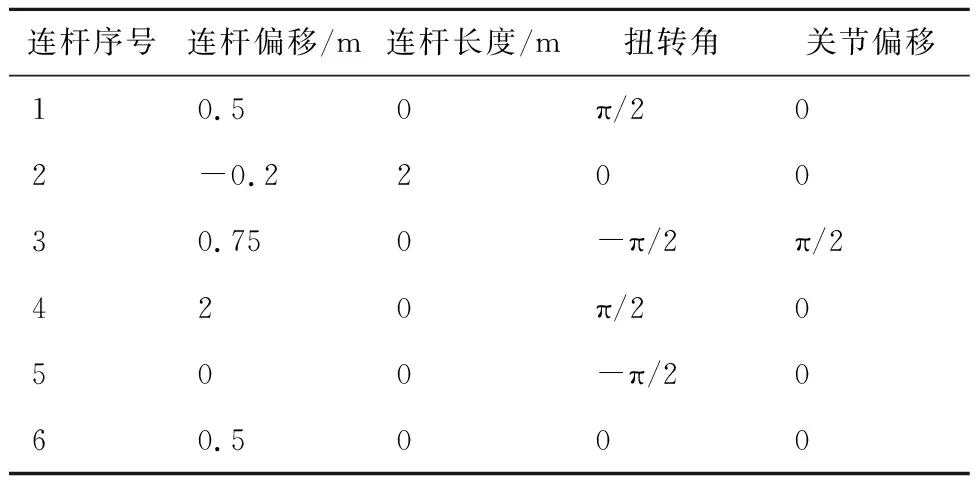
表1 空间机械臂DH参数Table 1 DH parameters of space manipulator
机械臂在非工作状态下采取收拢姿态,本文研究以此姿态作为空间机械臂初始状态,如图2所示。由图2可以看出,除了关节2有硬性幅度限制外,其余关节均无幅度限制。不失一般性地,设定关节2转角取值范围为[0,π],其余关节转角范围均为[-π,π]。机械臂动力学参数如表2所示,表中Ix、Iy、Iz分别为转动惯量在各轴的分量,Tc为关节转矩。
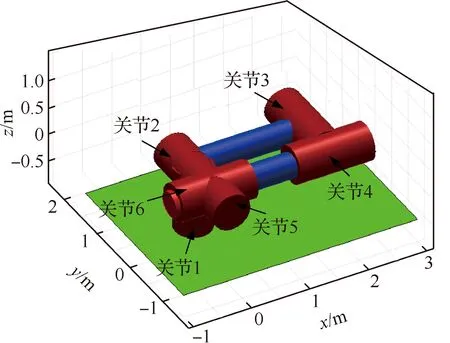
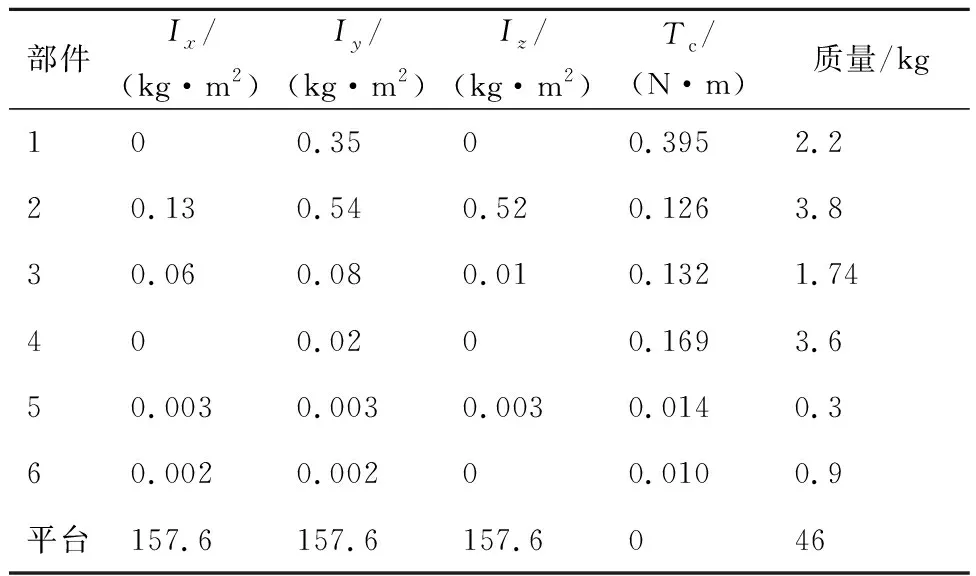
表2 空间机械臂动力学参数Table 2 Dynamic parameters of space manipulator
1.2 空间机械臂运动学模型
对本文研究的空间自由漂浮机械臂系统建立运动学模型,因为机械臂基座固定连接在航天器平台上,其在捕捉操作期间无控且不受重力影响,所以在机械臂执行动作期间会与平台产生动力学耦合情况。
由于推导过程较为基础,在此仅给出重要环节公式,具体的推导过程可参考文献[25]。针对文中机械臂,根据一般力学原理可得机械臂末端在惯性坐标系下的位置矢量re、速度矢量ve和角速度矢量ωe,具体表达式为
(1)
式中:r0为空间飞行器质心在惯性系中的位置矢量;b0为关节1相对于平台质心的位置矢量;ai为杆件i相对于关节i的位置矢量;bi为关节i+1相对于杆件i的位置矢量;v0、ω0分别为平台在惯性系中的速度矢量和角速度矢量;ki为关节i旋转单位矢量;ri为连杆i的位置矢量;qi为关节i的旋转角度;“·”表示求导。由于本文研究的机械臂末端关节有位置偏移,所以不能将关节质心作为末端位置进行捕捉结果判断。
对自由漂浮机械臂应用动量守恒分析,设定初始时刻线动量和角动量均为0,则得到以下多刚体系统约束:
(2)
式中:m0为平台质量;mLi和mJi分别为连杆i和关节i的质量;pi为关节i的位置矢量;I0、ILi、IJi分别为平台、连杆i和关节i的转动惯量矩阵;ωLi、ωJi分别为连杆i和关节i的角速度矢量。
本文为小型机械臂系统,关节质量较轻,在学习训练过程中可以将同一序号的关节和连杆视为整体,进而降低计算复杂度。由此得到自由漂浮机器人的动量守恒方程为
(3)

(4)
式中:rL0i表示杆件i指向平台质心的位置矢量;JTLi、JRLi分别为机械臂切向和径向转动惯量。
由式(3)和式(4)进一步推导求解,可得自由漂浮空间机械臂系统的运动学方程为
(5)
式中:Js为平台Jacobi矩阵;Jm为定基座机械臂Jacobi矩阵,此处不予赘述;re0为末端相对平台的位置矢量。
1.3 空间机械臂系统动力学模型
本文以拉格朗日法为基础推导动力学模型。机械臂系统的总动能为各部件动能之和,每个杆件和关节动能可由其质心线速度动能和转动角速度动能组成,则自由漂浮空间机械臂系统的总动能为
(6)
式中:mi为部件质量;vi为部件惯性系下速度矢量;Ii为部件转动惯量;ωi为部件角速度矢量。将1.2节中运动学方程代入可得:
(7)
其中:Hφ为定基座机械臂惯性张量矩阵,其表达式为
(8)
则有整个系统的拉格朗日动力学方程为
(9)
式中:cb为平台本体牵连速度的非线性项,本研究中设定为常值;cm为机械臂牵连速度的非线性项,本研究中设为常值;Fb为基体所受外力及外力矩,前文中已假设为0;τm为机械臂关节力矩。
2 多智能体深度强化学习轨迹规划
2.1 改进深度确定性策略梯度算法分析
因为载具平台处于自由漂浮状态,数学模型无法完全描述系统的非完整性约束。机械臂从收拢状姿态到捕捉姿态的轨迹规划可以看作其运动过程中一系列的动作决策行为,每个关节可视为一个决策智能体,最终的轨迹即为所有关节序列决策的集合。为了解决机械臂与环境交互无法精确建模和决策序列集合生成的问题,本文采用深度神经网络对捕捉轨迹规划策略进行逼近。
由于机械臂展开抓捕动作为连续动作,其用于评价的Q值函数不易精确设计,因此采用了策略梯度方法解决该问题。策略梯度算法可以通过最大化期望累积奖励来直接优化策略[26]。考虑到目标移动和环境的随机性,使用评价器拟合累积奖励,此评价器被称为Critic。针对机械臂关节运动取值连续,搜索空间较大的问题,为了缩小随机策略训练过程的样本空间,本文采用了确定性策略梯度方法。确定性策略梯度算法训练过程中同时学习Q函数和策略,对Q函数的学习是为了实现对环境适度探索。本文算法中执行器(Actor)和评价器(Critic)均采用双网络结构,分别称为决策网络和估计网络。在训练过程中直接对各自估计网络进行训练。决策网络由对应估计网络每隔一段时间进行优选后保存;评价器的决策网络同时输入所有智能体的联合动作和外部观测值,对自身某一动作对环境产生的影响进行评价。
下面将给出本文所用多智能体深度强化学习理论公式。深度强化学习过程中,智能体与环境进行交互,期间智能体的决策过程可以用马尔科夫决策过程(Markov Decision Process, MDP)进行描述。MDP模型是一个五元组(S,A,Ptrans,R,γ),分别对应于状态空间、动作空间、转移函数、奖励函数和折扣因子。对于第i个智能体的执行器Pi和评价器Qi的定义分别为
(10)
训练过程评价器策略优化的目标函数为
(11)
式中:E为贝尔曼方程;y代表当前累计奖励,由迭代而来,为区别于当前动作,累计奖励相关变量使用“′”表示。然后通过梯度下降法更新网络参数,对应的梯度计算函数为
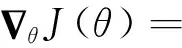
(12)
从式(12)可以看出策略损失的梯度即为策略函数梯度与评价函数梯度的近似数学期望。
为了提高训练效率,学习过程中设置了经验池机制,决策网络定期抽取经验池信息进行训练,考虑到经验池中案例质量分布不均,本文设计了一种优先抽取高质量经验的方法。设计如下经验案例抽取优先级Pr(k)公式:
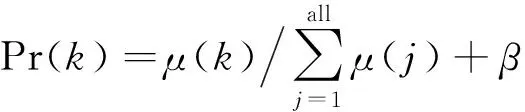
(13)
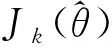
2.2 在线捕捉自学习系统设计
本文的主要工作聚焦于建立自学习系统,通过训练使漂浮机械臂具备自主捕捉轨迹规划能力。在2.1节中已经提到,对于每个智能体都将建立4个双隐层全连接神经网络:执行器的估计网络(ActorE)用于策略迭代更新;执行器决策网络(ActorD)用于经验池采样交互,其网络参数定期从ActorE处更新;评价器估计网络(CriticE)负责价值函数迭代更新,为当前ActorE的行为更新Q值;评价器决策网络(CriticD)负责计算全局奖励,其网络参数定期从CriticE处更新。训练系统架构示意图如图3所示,其中r1,r2,…,rn为各智能体的回报值。

本文采用集中训练分布执行的方式进行仿真,由于训练过程中评价器决策网络的输入为环境状态和所有智能体的联合动作,所以其输出的评价值函数已经包含了对多智能体协同的指导信息。分布式执行过程中各智能体执行器决策网络无需沟通,在训练回合数足够大的情况下,完全可以通过训练实现全部协同,而不需要再单独建立相关机制。但在未来算法改进中可以加入智能体交流机制,使得协同性进一步提升。
为了进一步提高算法执行效率,本文设计了以机械臂末端位置与目标相对距离dT和总操作时间t为参数的奖励函数:
(14)
式中:ep为动力学参数评价项。由式(14)可以看出,当目标距离越远则回报值越小,当操作用时越长则回报值越小,如果捕捉成功则获得固定回报值。对于任意智能体,环境交互得到的奖励值是相同的。评价器输入了联合动作信息,得到评价值不是只受单独关节动作影响。为了提高算法速度,超过关节运动限制的问题在运动学中处理,不计入奖励函数。
本文所述多智能体深度强化学习轨迹规划训练算法流程如算法1所示。

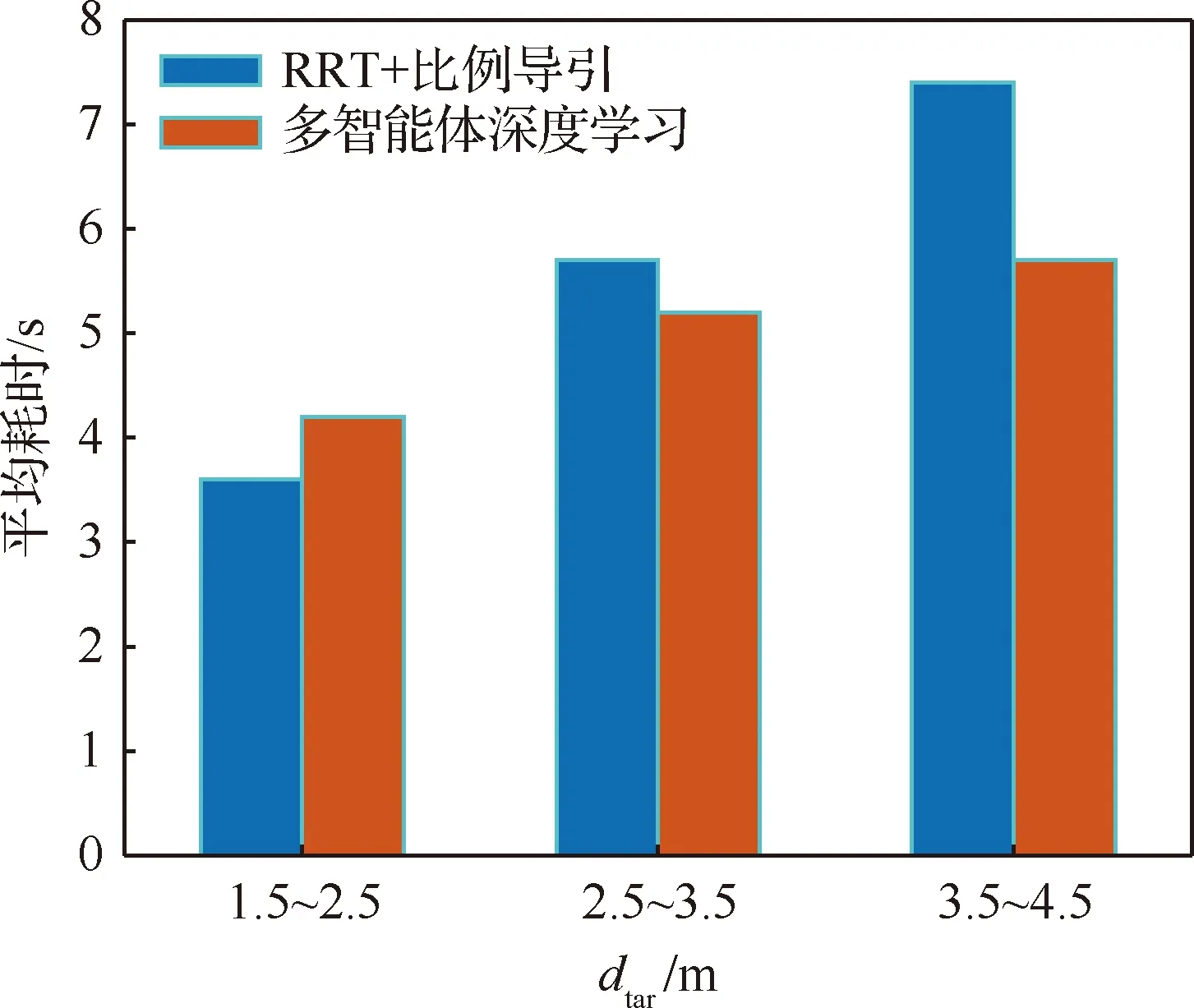
算法1 改进确定性策略梯度算法1.初始化各Agent的ActorE网络参数θpe、ActorD网络参数θpd、CriticE网络参数θQe、CriticD网络参数θQd2.初始化经验池ψ,设定各超参数3.for episode = 1 to Max_epi do4. 初始化环境S和各智能体网络参数5. 设定仿真步长step和最长仿真总时间Tsim6. 随机生成初始联合动作集合a=[a1 a2 … an]7. 更新状态S',得到初始奖励R0,将案例存储到经验池8. do while time i 从以上步骤可以看出,在每个回合中,评价器的决策网络能够接收全局信息,进而指导执行器更新网络,集中训练的协同性由此体现。规划算法通过环境、智能体执行器、智能体评价器三者交互来迭代训练策略网络。最终形成的智能体执行器决策网络θpd即为空间漂浮机械臂捕捉行为轨迹规划器。 操作系统环境为Windows10 x64,使用软件工具包版本为TensorFlow 2.1.0。硬件信息为Intel i5-9600K、GTX1060、DDR4 16 GB、240 GB SSD。网络训练环境是基于Python 3.7修改Open AI开源代码搭建的。仿真验证和数据处理均在MATLAB 2018b环境下实现。 在训练过程中,动力学模型计算后如果机械臂达到平台边界,则案例会被直接放弃,重新选择动作。空间匀速直线运动小球的初始位置随机选择在以基座质心为球心,半径为5 m的半球形包络内,速度vtar取值不超过0.4 m/s,速度方向矢量与小球位置矢量ptar有如下关系: (15) 式中:dtar为球心与基座间距离;p0为基座位置矢量。 仿真中每个智能体4个神经网络均采用双隐层32节点全连接网络。各神经网络的输入输出信息参见表3,其中关节末端位置由机械臂正运动学解算得出。 表中的联合动作指所有智能体的动作合集,联合动作奖励值即为环境反馈的动作奖励值,仅是为了区分输入给对应网络。从表3中可以看出,执行器和评价器的神经网络均为高维输入低维输出。执行器神经网络要完成空间坐标向角度映射,所以激活函数采用tanh函数。评价器网络仅为数值求解,本文采用常见的sigmoid函数作为激活函数。 本文采用文献[16]中滚动RRT+比例导引算法作为对比算法,该算法将目标捕捉过程分为2个多约束阶段,在初始阶段使用滚动RRT算法提高搜索能力,在捕捉阶段使用比例导引算法提高接近速度。该方法技术细节可参照文献[16],不予赘述。 表3 各神经网络输入输出参数Table 3 Input and output parameters of neural networks 由于本文中算法没有完整数据集可以用作对比分析,评价算法优劣的方法主要有2个方面:① 奖励值曲线变化趋势,最终奖励值越高则算法越好,奖励值曲线收敛速度越快则算法收敛性越好;② 算法所得决策网络在环境下的表现,动作执行情况越好,则算法性能越好。因为没有类似自学习规划算法可以进行比较,所以在后文仿真中,重点对比了决策网络在实际场景中的表现情况,作为算法主要评价依据。 本文算法可以用平均回报值方差或结果误差值方差判断作为终止条件。但设定此条件后,总训练回合数随机性过大,无法进行对比展示。所以采用人为确定回合数。仿真实验首先对经验案例有无优先抽取机制进行了仿真,经过20万回合训练后,得到平均奖励随训练回合数增长曲线如图4所示。图中绿色曲线训练时采用了优先级抽取机制,蓝色曲线训练过程中未使用优先级机制。由图可知当采取案例优先抽取机制时,平均奖励曲线收敛速度得到了较大提高。 通过增大仿真回合数检验算法收敛趋势。经过25万回合的仿真训练后,得到如图5所示的平均奖励曲线,图中蓝色曲线为15万回合自学习训练过程平均奖励值曲线,红色曲线为25万回合训练平均奖励值曲线。 因为使用了相同的多智能体强化学习算法,可以看到两个曲线趋势大体相似。但红色曲线在21万回合附近训练后期,出现了严重的过拟合现象。分析该现象产生原因,因为机械臂系统具有完整的约束模型,且训练过程中不存在外部扰动或噪声,所以分析认为是空间小球目标的初始位置随机性波动也被学习系统训练学习了。 多智能体强化学习系统训练结束后,执行器的决策网络训练成型。设定空间小球的初始位置为ptar=[-1,-0.5,5.8] m,运动目标的初始速度为vtar=[-0.082,-0.037,0.042] m/s,分别使用该规划决策器和滚动RRT算法对该场景进行机械臂轨迹规划仿真,得到仿真曲线。图6为多智能体规划决策器规划生成的捕捉过程各关节转角曲线,图7为对比算法生成的关节转角曲线。 对比图6和图7可以看出:在同一场景下,本文提出的算法用时约为5.6 s,而对比算法规划耗时约为7.4 s,可见本文算法规划效率更高。文中所提出的算法规划所得曲线较为平滑,而对比算法规划所得关节转角曲线相对较粗糙。相比之下,本文算法鲁棒性更强。 2种算法在规划前期曲线都存在抖动。本文所述算法前期抖动的原因是无法直接跟踪移动目标,且机械臂展开初始阶段存在多种可能构型,所以产生了曲线抖动现象,随着捕捉过程的推进,曲线逐渐变得平滑。而对比算法前期抖动较为明显,因为该算法规划前期使用RRT方法,该方法具有随机搜索特性,在初始阶段就产生了非必要的探索行为,中期算法交替时又耗费时间进行轨迹误差补偿,这是影响算法效率的因素之一。对比算法规划后期因为使用比例导引方法,规划效率明显提高,且关节角曲线趋于平滑。 图8为本文算法在该仿真场景中规划所得轨迹对应的平台姿态扰动角曲线图,扰动角曲线并非在决策器规划过程中决定,而是规划轨迹生成后由动力学模型解算得到。从图8中可以看出,机械臂捕捉动作对漂浮平台的扰动较小,各向扰动角度均不超过10°,由此也可看出本文算法的有效性和可行性。 为了进一步揭示空间目标与机械臂基座距离和捕捉轨迹规划耗时的关系,分别对2种算法进行了1 000组不同初始状态的规划仿真,对仿真结果进行统计分析,在1.5 m≤dtar<2.5 m时本文算法捕捉规划平均耗时4.2 s,对比算法平均耗时3.6 s;在2.5 m≤dtar<3.5 m时本文算法平均耗时5.2 s,对比算法平均耗时5.7 s;在3.5 m≤dtar<4.5 m时本文算法平均耗时5.7 s,对比算法平均耗时7.4 s。于是得到如图9所示柱状图。从图中可以看出,在目标距离较近时本文算法规划轨迹较慢,此时RRT+比例导引方法规划效率更高。随着距离增加,本文方法规划效率有所提高。分析其中原因,RRT的随机搜索方法在短距离规划中具有一定优势,其在长距离规划中必然会消耗更多时间来探索执行空间,所以长距离规划中效率不如本文算法。 对上述1 000次仿真中2种算法耗时情况进行统计,本文所述算法得到平均捕捉完成耗时为5.4 s,对比算法平均耗时为6.3 s,由此可见本文算法规划效率更高。 1) 本文在机械臂运动学和动力学分析基础上,提出了基于多智能体系统的强化学习机械臂轨迹规划方法。 2) 应用本文算法可以快速对空间捕捉问题进行规划和处理,平均捕捉动作完成耗时5.4 s,相比前人算法规划效率更高。 3) 仿真结果表明,本文算法规划所得轨迹曲线更平滑,相比前人算法鲁棒性更强,具有很强的实际工程应用价值。3 仿真数据与分析
3.1 仿真条件
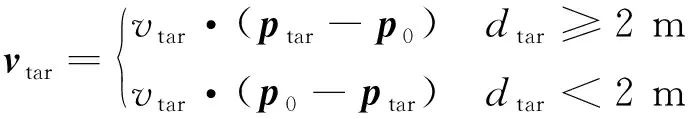
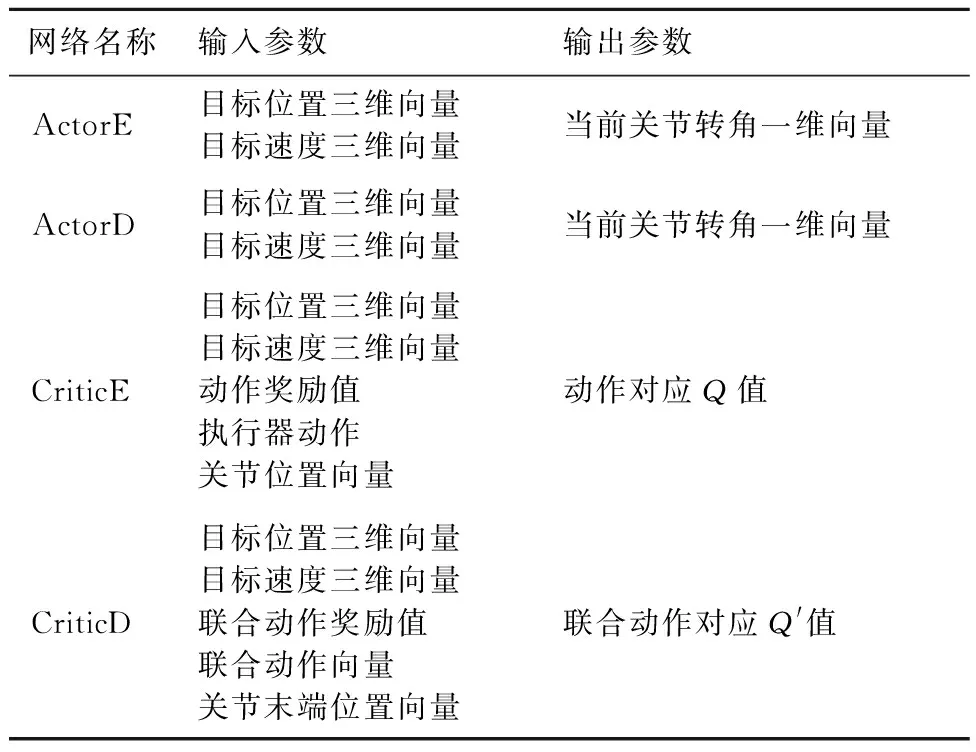
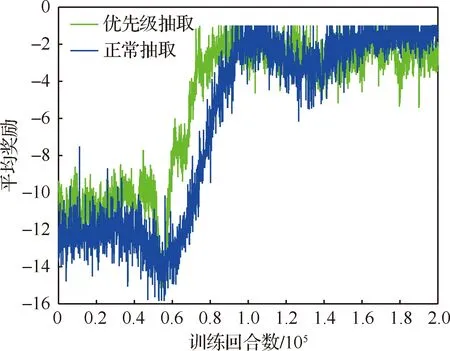
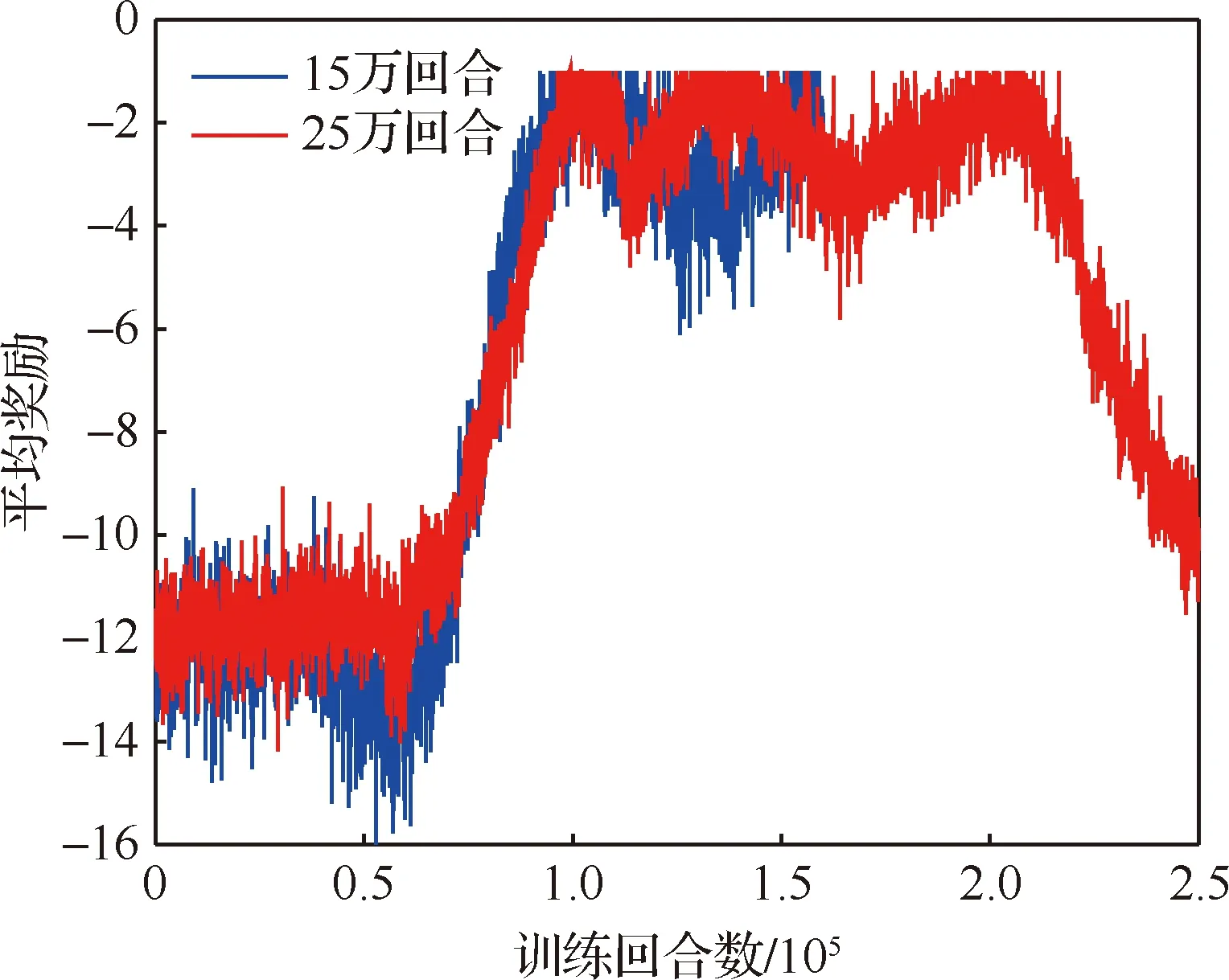
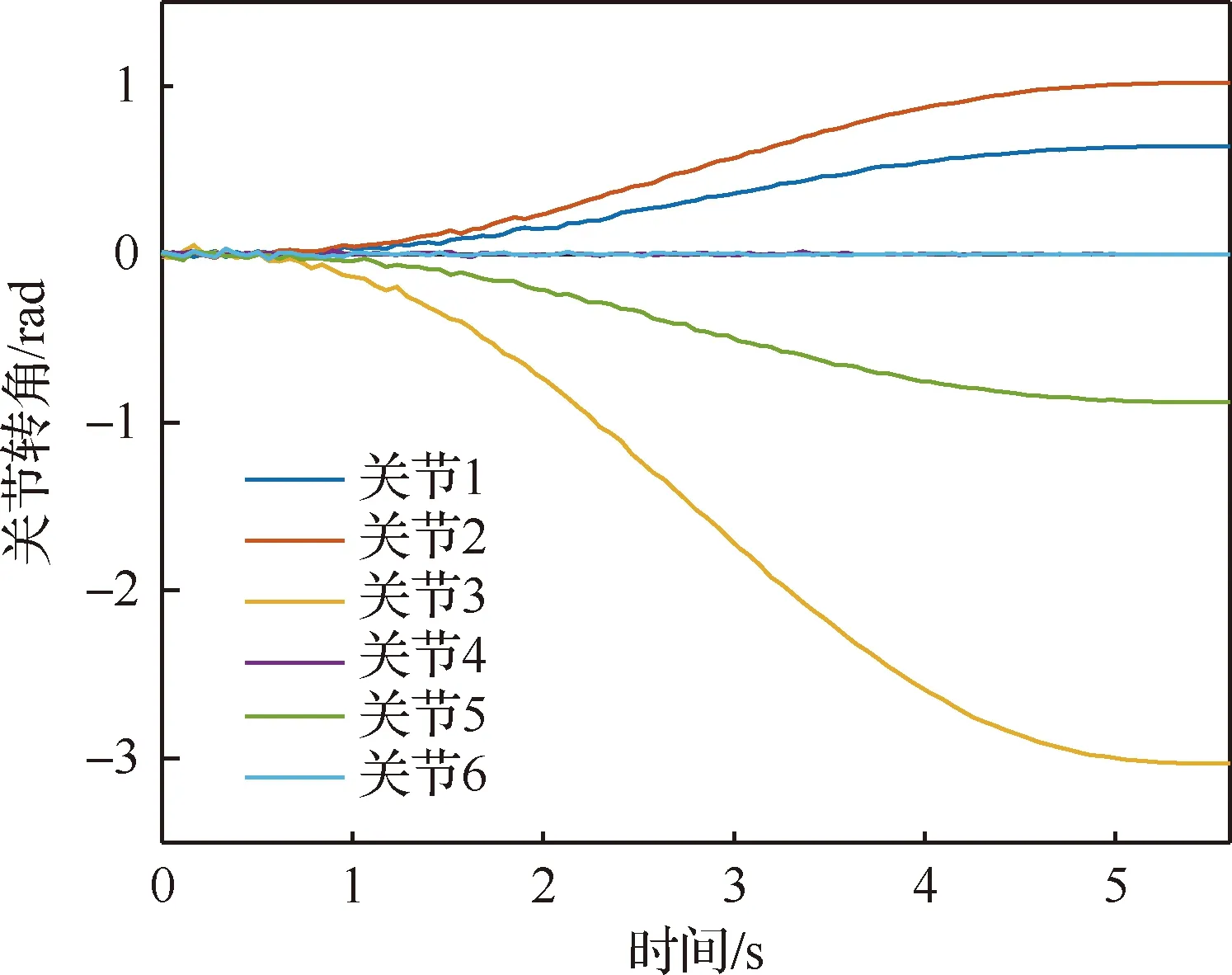
3.2 仿真结果与数据分析

4 结 论

