超声导波正轨动态检测信号畸变矫正算法研究

张鹏飞 赵 波 唐志峰

（1.浙江大学制造技术及装备自动化研究所，杭州310027；2.北京铁科英迈技术有限公司，北京100081；3.浙江大学生物医学工程与仪器科学学院，杭州310027）

0 引 言

随着中国铁路设施建设的日趋完善，针对铁路轨道的结构完整性检测愈受重视。传统的钢轨检测采用超声探伤小车，但探伤小车上安装的组合式超声探头难以检测钢轨中存在的垂直于钢轨走向的横截面损伤以及钢轨轨头踏面的鱼鳞纹。作为传统超声探伤的盲点，这些种类的伤损导致的断轨事故却时有发生。超声导波检测利用了超声导波传播距离远，覆盖范围大的优点，在钢轨探伤中能够完整覆盖钢轨横截面并且对横截面损伤尤为敏感，克服了传统超声探伤的缺点，因而在钢轨无损检测领域具有非常广阔的应用前景［1］。

针对钢轨缺陷的导波检测，国内外学者已经开展了相关的研究。Rose 等研究了超声导波针对钢轨轨头的缺陷的检测的可行性，并利用半解析有限元技术分析了导波在轨头传播的频散曲线，探索适合在轨头传播的超声导波模态和频率［2］。王彭等提出了一种利用钢轨裂缝反射系数和波幅分解的方法，检测断轨并能实现精确定位，在2.8 m长的含有裂缝的实验钢轨上，取得了较好的效果［3］。胡剑虹等针对钢轨轨底的缺陷检测，提出了基于磁致伸缩原理的超声导波换能器的设计方案，通过实验验证了该方案的可行性，并通过有限元分析确定了适合于检测钢轨轨底缺陷的超声导波频率［4］。G.Konstantinidis 等在板状结构的监测中，提出一种基于最优基准信号的差值算法，以克服温度对监测的影响［5-6］。Chang Liu等针对变化的环境，提出一种通过奇异值分解的差值运算，实现缺陷精确定位的算法［7］，而在钢轨导波检测信号的畸变矫正处理算法研究方面还鲜有报道。

本文针对钢轨超声导波动态检测信号的特点，提出了一种钢轨超声导波动态检测回波畸变矫正算法。算法以噪声概率分布为依据，结合了希尔伯特变换、线性插值、局部最大相关性、波幅调整等多种处理方法，能有效克服温度变化、电压不稳定等多种影响因素导致的回波信号畸变，为准确判断钢轨的结构完整性状况提供了保证。经实验验证了该算法的有效性。

1 钢轨超声导波动态检测系统

1.1 系统组成

钢轨超声导波动态检测系统主要包括钢轨导波探伤轮、检测主机和上位机。钢轨导波探伤轮基于压电原理，用于激励和接收导波；检测主机由激励单元、功率放大单元、前置放大单元、信号处理单元和计数器组成，主要负责激励探伤轮、采集钢轨回波并上传至上位机；上位机下发控制参数并接收检测信号并进行后续信号处理、储存和展示。系统拓扑结构如图1 所示。系统可在钢轨上运行，在运动过程中进行导波检测，由计数器确认检测位置，典型检测信号如图2和图3所示。

1.2 导波探伤轮和导波信号激励

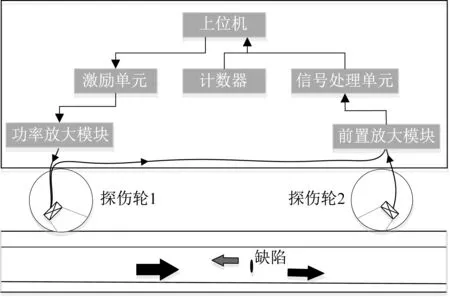
图1 钢轨超声导波动态检测系统Fig.1 The rail guided wave dynamic detection system

图2 现场测试照片Fig.2 Field test

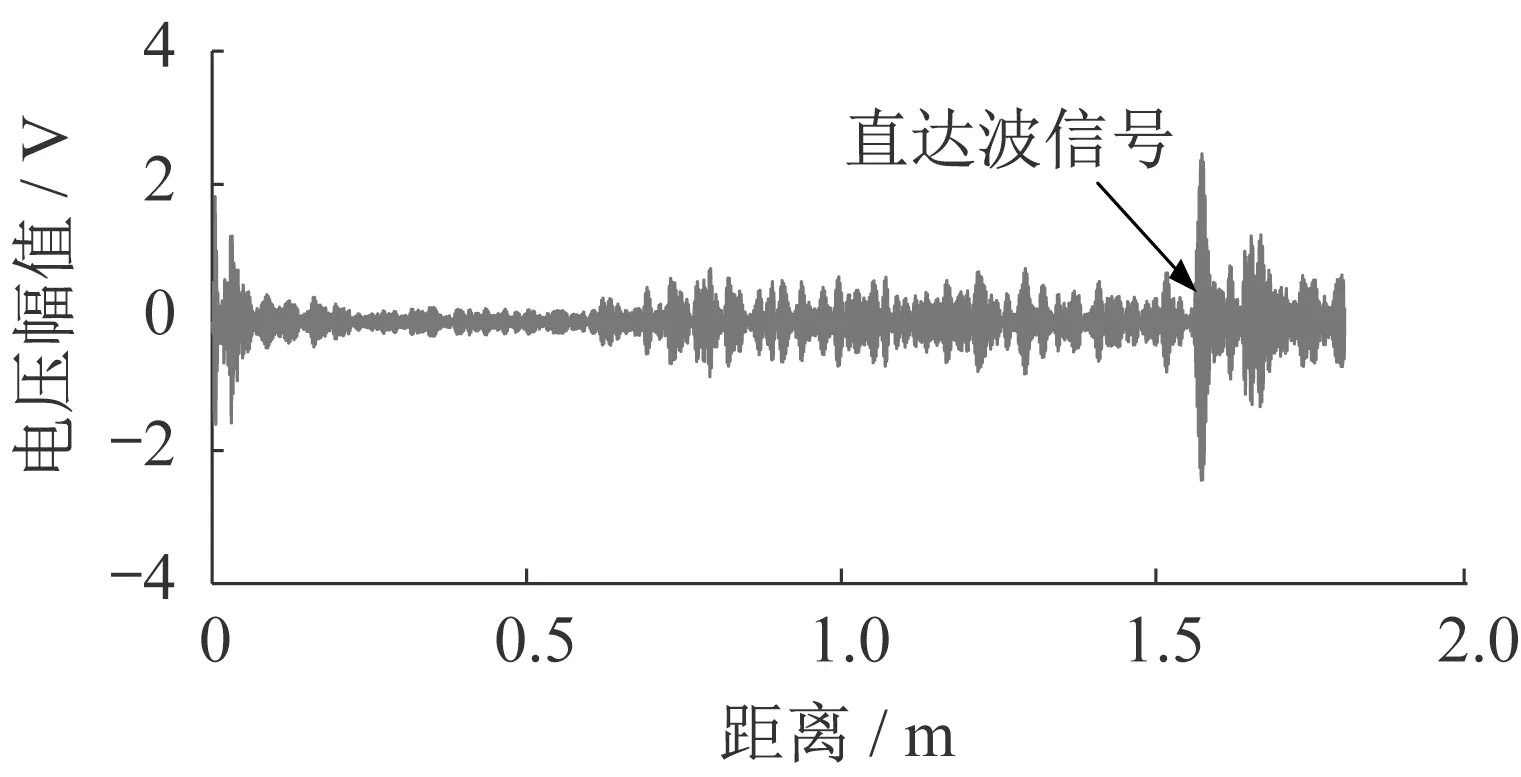
图3 实测信号Fig.3 Measured signal

导波探伤轮由压电式换能器、内部夹具和外部探伤轮组成。探伤轮采用动密封结构，保障轮子在运动过程中的内部密封性，压电式换能器由低频电脉冲信号激励产生振动通过耦合液和透射橡胶再经过水耦合进入到钢轨中从而激励出导波，导波沿着钢轨传播被另一个探伤轮接收到，如果传播路径上存在损伤，则直达波信号会出现幅值下降，通过有无损伤情况下接收信号的对比可确认是否存在伤损。经ABAQUS 仿真研究和实验，认为诸如64 K 的中低频超声导波在保证检测灵敏度的同时，更适合于钢轨的缺陷检测，因脉冲回波式检测中受到探轮内部和钢轨轨底的导波反射的影响，信号较为复杂，因此本文中采用单发单收的形式进行检测。

2 信号处理

2.1 基础算法模型

超声导波信号噪声分布实验表明，检测系统中的噪声是近似于均值为0 的随机噪声，噪声概率密度谱如图4所示。

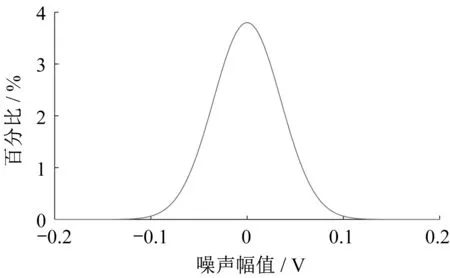
图4 检测系统中随机噪声的概率密度Fig.4 The probability density of random noise in the detection system

对于特定功率和增益下的回波信号，可以简单表示为

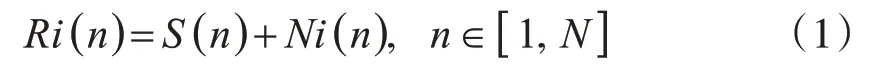
式中：Ri(n)表示第i 次测量接收到的回波信号；S(n)是钢轨的真实回波信号；Ni(n)是第i 次测量中的随机噪声；N是总的采样点数。

若在相同的条件下，对连续M 次测量做平均运算，根据随机噪声均值为0的性质，在M 足够大的情况下，可以得到S(n)的近似表示，即有

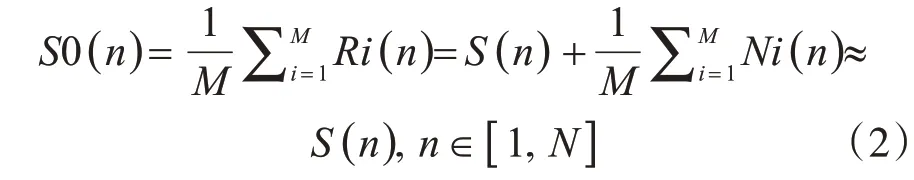
式中，S0(n)表示相同条件下M 次测量结果的平均。

因此，若以S0(n)作为参考信号，对于任意一次的测量结果Ri(n)，做差值运算：

实际测量中，式（3）成立的条件是苛刻的，温度、检测系统的电压漂移、加载导波的条件、边界条件等都是差值运算中需要考虑的影响因素［1］。参考信号S0(n)与Ri(n) 任意位置处的瞬时相位保持一致，是差值运算Ri(n)-S0(n)≈Ni(n)成立的必要条件。但由于温度等影响因素的存在，测量信号和参考信号中的瞬时相位不可能总是保持一致，这就导致差值运算的结果不再近似于随机噪声的分布。

利用希尔伯特变换后的幅值序列代替原时间序列，不仅同样能反映信号瞬时能量分布，而且在差值运算过程中，一定程度上减小了瞬时相位的偏差引起的运算误差。通过希尔伯特变换求解解析信号并取模，即得到幅值序列。令H表示希尔伯特变换，并返回变换序列的解析信号，令||表示取模运算，根据希尔伯特变换的线性时不变性质，有

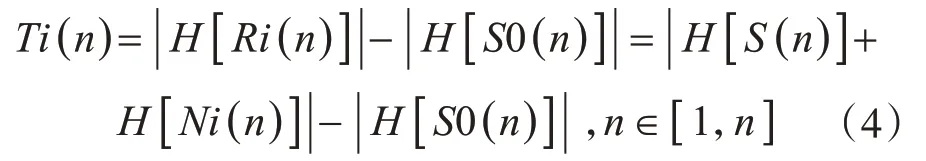
另，根据式（2）有

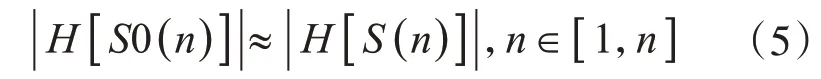
根据矢量的加减运算性质，结合式（5），对式（4）求取值范围，则有

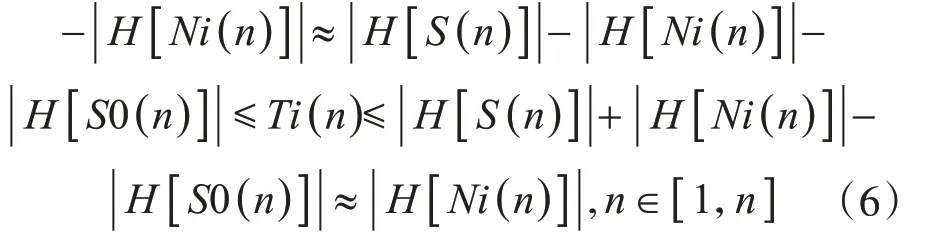
式（6）表明，用希尔伯特幅值序列做差值运算时，差值近似且小于随机噪声的希尔伯特幅值序列（图5）。因此，记随机噪声的希尔伯特幅值序列的概率分布函数为F(x)，表示噪声的希尔伯特幅值序列中幅值不大于x 的概率。显然，F(x) ≤1。若合理设置阈值Threshold，使得p=F(Threshold)接近于1，则如果在连续K 次测量中，都存在采样点n0，满足：

则可以1-(1-p)K的概率认为，钢轨在该采样信号对应位置存在缺陷。

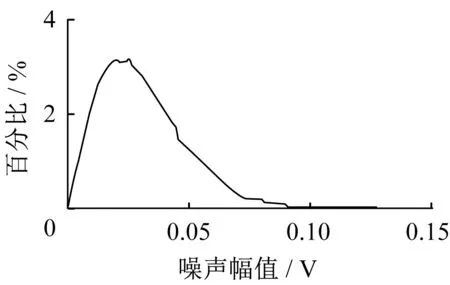
图5 噪声经希尔伯特变换后的幅值序列Fig.5 The amplitude sequence of the noise through Hilbert transform

2.2 温度补偿

引入希尔伯特变换和取模运算并不能从根本上解决瞬时相位的偏差带来的运算误差。实际测量中，温度作为差值运算最重要的影响因素所产生的误差，需要通过进一步的处理予以补偿。

2.2.1 温度变化的影响

在温度变化对超声导波传播的影响的研究中，Weaver 和Lobkis 认为温度变化对超声导波信号产生一个在时域上拉伸或压缩的作用［8］。轨温升高声速变大，近似于在时域上对波形拉伸；轨温降低声速变小，近似于在时域上对波形压缩。Tindaro Cicero 针对不同温度下，相同距离处的回波的时移进行分析［1］。考虑温度变化δT，其他条件相同的情况下，距离发射位置d处的回波的时移δt，对式t=求偏微分得：

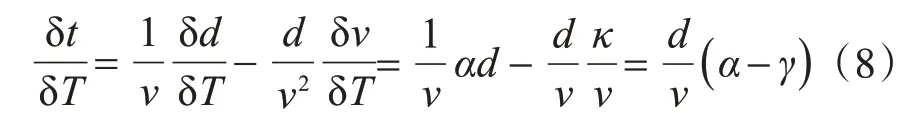
式（8）表明，温度变化导致钢轨中导波的声速的变化是引起回波时移的主要原因。且时移的大小与传播的距离成正比。距离发射端越远，在相同温度变化的情况下，回波的时移越大。而回波的时移即意味着测量信号与参考信号之间会产生瞬时相位的偏差。

2.2.2 温度补偿策略

单发单收的模式下，初始脉冲峰值点常作为参考点，来估计声速变化对波形整体伸缩变化的影响［6-7］。通过参考点计算出声速对整体波形的伸缩变化的影响的情况下，以线性插值运算拉伸或压缩波形，使得测量信号直达波与参考信号直达波对齐，以保证测量信号与参考信号的瞬时相位在整体上保持一致（图6（a））。

由于温度变化对不同距离处产生的时移效果不同，为保证测量信号与参考信号在局部位置上瞬时相位均保持一致，需要针对局部位置精确计算时移，以保证差值运算得到最小误差。

针对上述的情况，给出下述的基于极小值分段和基于局部最大相关系数求时移的处理算法：

步骤1：给定最小段长MinLen，对差值运算后的信号，以极小值点分段，且保证每段不小于MinLen，记 第i段 信 号 为Meas(i)，总 段 数M，Meas(i)的最左值位置为left。

步骤2：对于每段信号Meas(i)，求取参考信号对应位置附近等长的最佳匹配Ref(i)，使得Meas(i)和Ref(i)相关系数最大，此时left相对于Ref(i)的最左值位置的偏移量offset(i)即为局部信号的时移。

步骤3：差值运算求取每段信号的差值：Diff(i)=Meas(i)-Ref(i)，i∈[1，M]。以 极 小 值点分段，相比于以固定值分段，可以避免完整的信号包络被分割至两个不同信号段的现象发生，从而减少对后续基于局部相关系数确定时移的影响。考虑发射脉冲的频率f、周期数cycles和采样率fs，可以估算出发射脉冲包含的采样点数count=round(fs×cycles÷f)，因而一个完整的回波包络包含的采样点数应不小于count。这对最小段长MinLen的选择有一定的指导意义。

实际应用中，为进一步补偿温度变化的影响，还可以在不同轨温下获取多组测量信号，分别作均值运算，得到不同轨温下的参考信号集。对于任意的测量信号，从参考信号集中选取与测量信号的简单差值的均方根最小的信号为最佳匹配参考信号。并以该最佳匹配参考信号与测量信号做温度补偿处理，差值运算后得到真实的运算结果（图6（b））。

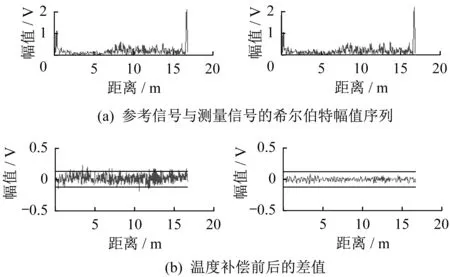
图6 温度补偿前后的差值运算效果比较Fig.6 Comparison of difference operation before and after temperature compensation

2.3 能量补偿

通常情况下，检测系统电源等的不稳定性，会导致不同测量信号能量的略微差异。此外，压电式换能器的压电晶片在长期工作条件下的老化作用，从而导致测量信号能量的减小。

考虑上述两种情况，若初始监测时，钢轨的真实直达波信号为S(n)，引入能量因子∂，改进式（1），则任意一次测量的回波信号可表示为

初始检测时，能量的变化主要是系统电源等的不稳定性引起，此时有∂≈1.0。经过相当长的时间后，能量的变化主要由晶片长期工作引起，此时∂逐渐减小。通过测量信号与参考信号的直达波峰值比较，或整体波形的幅值比较，可以很方便地计算出能量因子∂，记

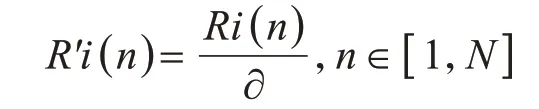
则式（3）变为

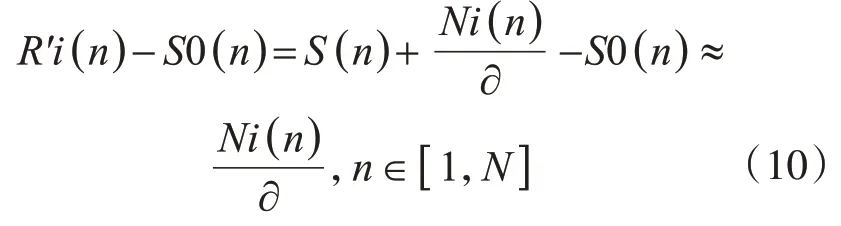
且式（6）变为

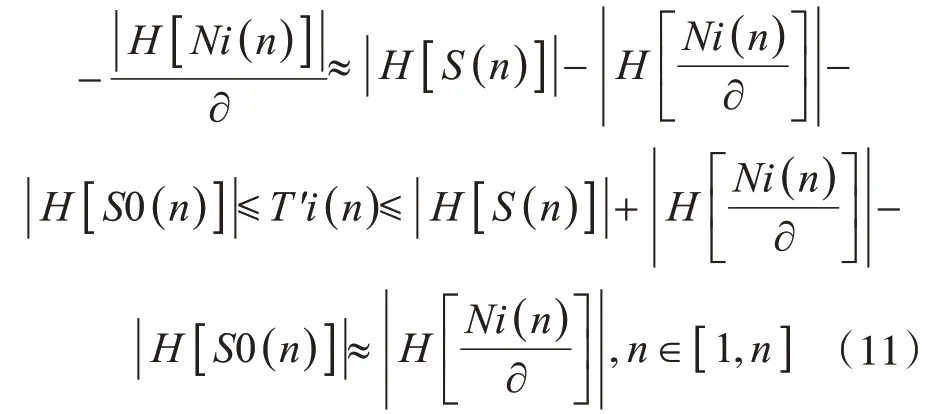
上两式表明，能量因子的引入，虽然补偿了晶片连续性工作引起的信号能量减弱，但同时也导致差值运算后的差值误差增大。不过，可以认为在∂足够大接近于1.0 的情况下，使用式（11）的方法检测缺陷，增大的误差带来的影响可以忽略不计。

2.4 无关信号

检测时旁边轨道有列车通过时，电磁干扰会对采集系统产生很大的影响，此时接收到的检测信号，不能作为有效的检测信号，应予以排除。实验表明，对于有效的测量信号，其与参考信号的相关系数|ρ|≥0.9（图7）。通过对回波信号和参考信号的希尔伯特幅值序列求相关系数，能有效地区分列车通过时候的信号。

图7 列车通过时的信号，其相关系数|ρ|=0.0966Fig.7 The signal when the train is coming，correlation coefficient|ρ|=0.0966

3 结 论

基于超声导波的钢轨动态检测系统为钢轨的结构完整性和安全性检测提供了一个有效的补充手段。必须指出的是，导波信号是对环境变化极其敏感的，对导波信号影响的最主要因素就是环境温度的变化。除了温度以外，检测系统的电压漂移、加载导波的条件、列车通过时的电磁干扰等都是不可忽视的影响因素。稳定有效的检测信号是保证良好检测效果的前提，本文提出的信号矫正算法能有效克服这些因素对检测信号稳定性和可靠性的影响。