波形钢腹板组合桥梁夹层梁模型

陈夏春 白植舟 姜瑞娟 区达光 陈德伟

（1.深圳市尚智工程技术咨询有限公司，深圳518000；2.同济大学桥梁工程系，上海200092；3.山东大学土木工程系，济南50061；4.深圳市市政设计研究院有限公司，深圳518029；5.香港大学土木工程系，香港）

0 引 言

波形钢腹板组合箱梁是一种新型桥梁结构（图1和图2），由混凝土顶底板与波形钢腹板连接构成，通常设置横隔板，以及体内与体外两种预应力束。波形钢腹板较传统平钢腹板有更高的抗屈曲能力，因此可以减小腹板的厚度，同时可以有效减少加劲肋的使用和相关焊接工作量，避免疲劳破坏，且有利于后期维护。波形钢腹板厚度较传统的平钢腹板和混凝土腹板小，因此梁自重更小，从而使得桥梁跨度可以更大。由于显著的“褶皱效应”，波形钢腹板的轴向刚度很小，因此预应力可以更有效地施加在混凝土顶底板上，防止其开裂，提高了预应力效率。传统组合桥梁在负弯矩区较容易出现混凝土受拉开裂的问题［1-2］，采用轴向刚度忽略不计的波形钢腹板可很大程度上解决这个问题。近三十余年，波形钢腹板组合桥梁在法国、日本、德国、韩国、中国等国家得到广泛地推广和应用。

图1 波形钢腹板组合桥梁构造Fig.1 A prestressed concrete bridge with corrugated steel webs

国内外众多学者已经对波形钢腹板组合桥梁的受弯性能开展了较广泛的理论与试验研究，取得了许多有价值的研究成果。

由于波形钢腹板剪切刚度小及轴向刚度可以忽略不计的特点，平截面假定对于该类桥梁不适用。因此，传统的欧拉梁和铁木辛柯梁理论可能不适用于该类桥梁［3-5］。为了模拟该类桥梁的弯曲与剪切性能，Kato等［6］假设所有的剪力由波形钢腹板承担，弯矩全部由混凝土顶底板承担，将挠度和腹板转角作为独立的位移变量，但低估了顶底板承担的剪力。应用变分原理，Machimdamrong等［3-4］推导出了一种梁理论（称为G3 理论），将挠度、顶底板转角、腹板转角作为三个独立的位移变量。吴文清等［7］提出“拟平截面假定”，简化计算，以便进行设计。聂建国等［5］未采用平截面假定，而是将弯曲行为分解为桁架作用和弯曲作用进行分析计算。国内的其他学者也做了大量的弯曲及剪切研究工作，例如苏俭［8］、李立峰［9］、贺君［10］、冀伟［11］、张鸿［12］、武海鹏［13］等学者。

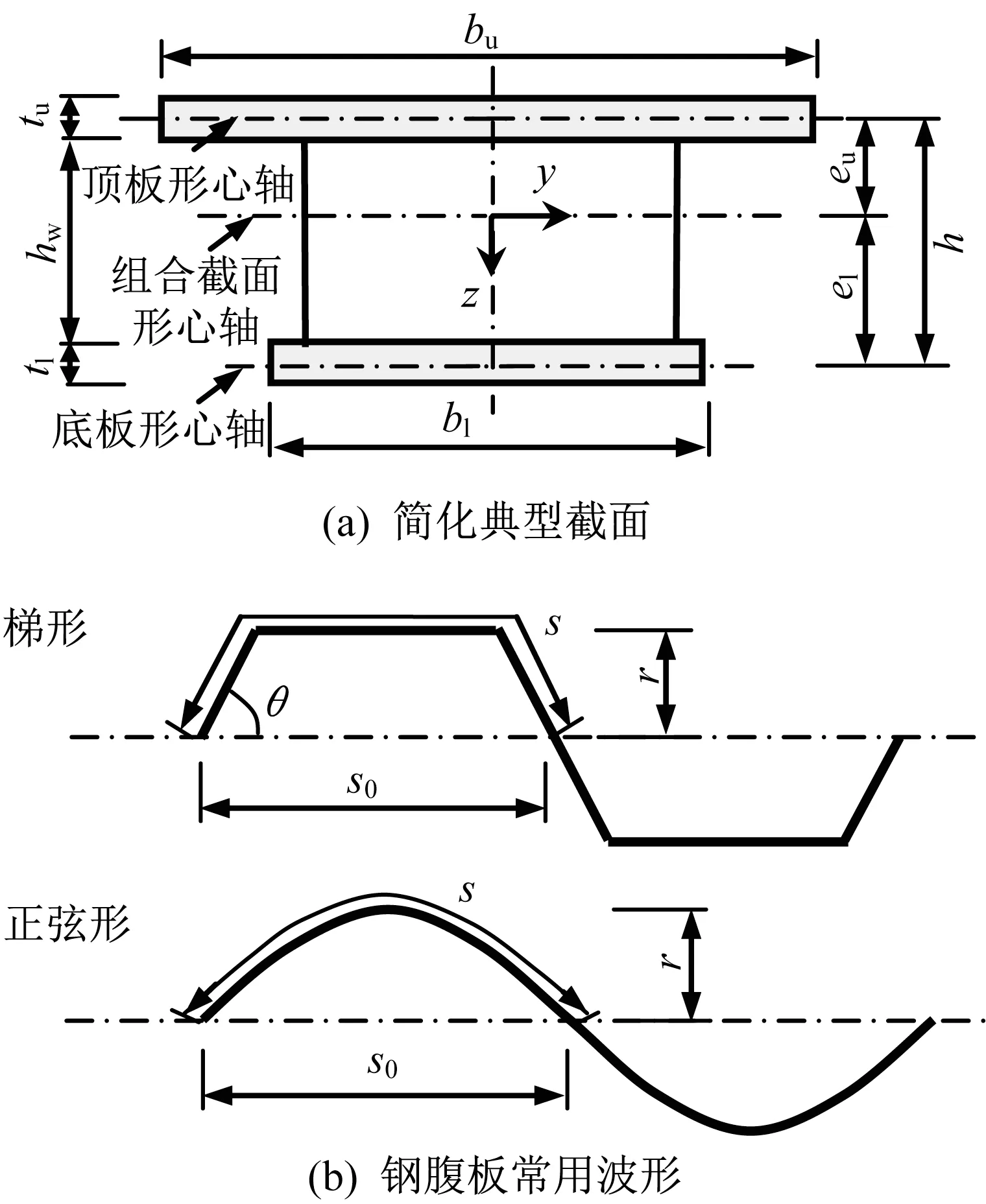
图2 波形钢腹板组合桥梁截面与腹板波形Fig.2 Cross section configuration of bridge

在设计中，通常假设所有的剪力仅由波形钢腹板承担［14］。但是，该假设仍然存在争议。基于对波形钢腹板组合桥梁缩尺模型的试验和有限元分析，Shiratani 等［15］发现悬臂梁波形钢腹板承担的剪力在梁体支撑端附近明显减小，但是悬臂梁截面和作用在组合截面的总剪力沿梁长是不变的。试验结果表明支撑端波形钢腹板承担的剪力比率在混凝土顶底板开裂前约为35%。随着荷载增加和裂缝的发展，在波形腹板屈服前该比率也只增加至约45%。但是试件在离支撑端2 m 位置处，波形钢腹板承担的剪力比率在混凝土顶底板开裂前约为72%，并随着荷载增加和裂缝发展，在波形腹板屈服前该比率增加至约88%。Kadotani等［16］通过试验研究了组合截面混凝土顶底板与波形钢腹板之间剪力承担比率沿梁长方向的分布。一个简支梁试件静载的试验结果表明，整体上来说波形钢腹板承担的剪力比率约为65%，然而在跨中集中荷载附近这一比率降低至仅约35%。

虽然国内外众多学者对波形钢腹板梁的弯曲和剪切性能已取得丰硕的成果，但对于剪力在组合截面混凝土顶底板与波形钢腹板之间的分配比例的研究还不足，仍存在明显分歧。其原因是目前尚缺乏完整的梁理论模型分析混凝土顶底板局部弯曲与波形钢腹板耦合作用的影响，以及横隔板的作用。因此，本文考虑混凝土顶底板的局部弯曲，以及该局部弯曲与波形钢腹板剪切变形的耦合作用，建立了一个适用于该类桥梁的夹层梁理论模型。该模型亦同时考虑横隔板的作用；并基于提出的夹层梁模型，进一步提出了一种有限元梁单元，方便进行实际工程设计计算；最后通过试验的方法对建立的夹层梁理论模型进行了验证。

1 夹层梁模型

传统夹层梁模型（sandwich beam model）很早应用在航空航天和船舶领域［17］。波形钢腹板组合桥梁与这些领域的夹层梁（图3）受力特征非常类似。夹层梁主要由刚性上面层、刚性下面层及中间轻质芯材层构成。该类桥梁的波形腹板和夹层梁中间轻质芯材层的轴向刚度都可忽略不计，主要承受剪力；该类桥梁的混凝土顶底板和夹层梁上下面层主要承受弯矩。不过，两者仍存在一些小的差别。该类桥梁的腹板很薄，然而夹层梁的中间轻质芯材层沿宽度方向均匀分布。另外，该类桥梁会设置一定数量的横隔板。因此，需要对航空航天和船舶领域的传统夹层梁理论模型进行一些修改，以应用到该类桥梁。

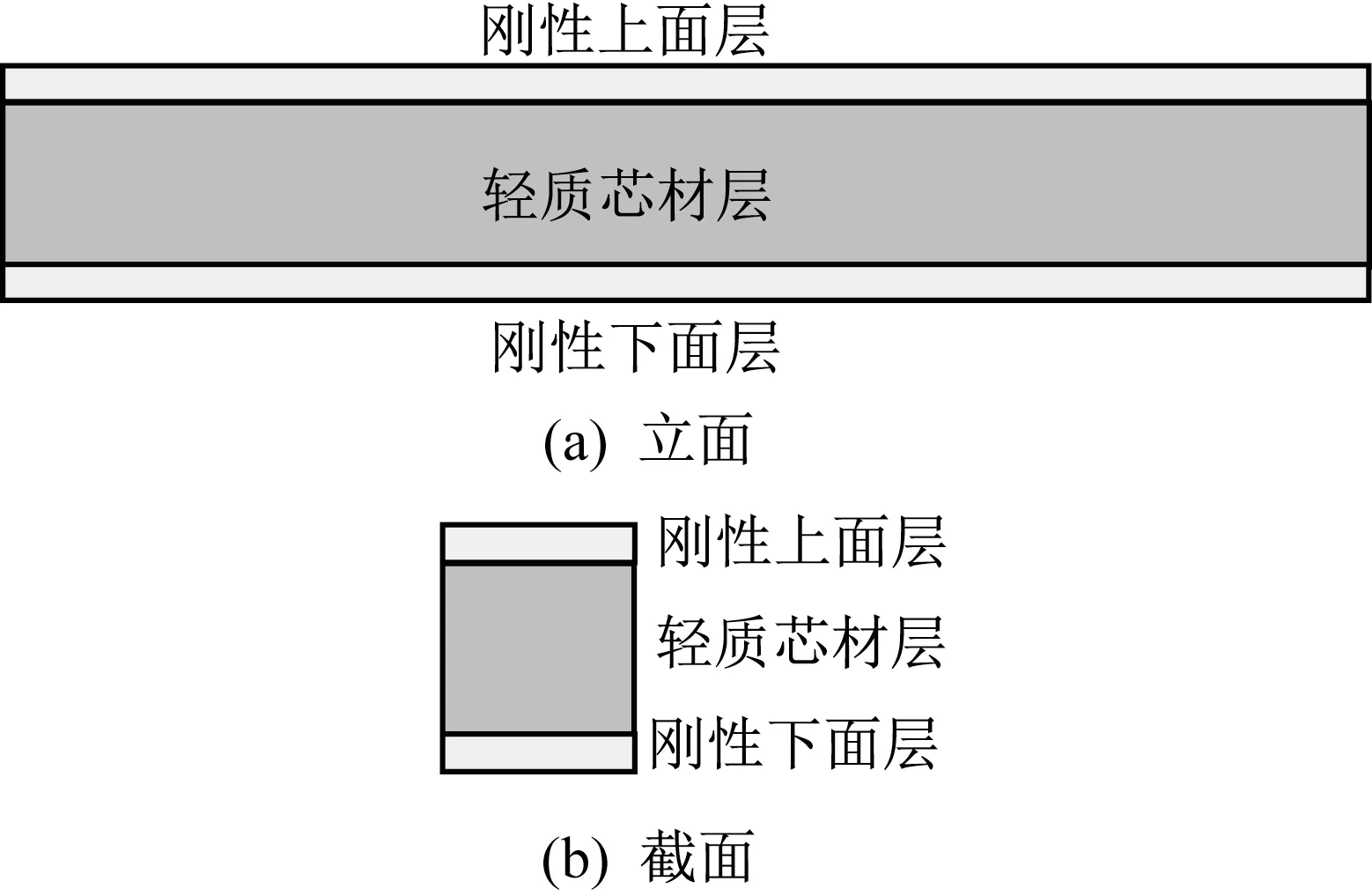
图3 传统夹层梁结构Fig.3 A simple sandwich beam structure

1.1 梁段控制方程

波形钢腹板组合梁的梁段变形如图4 所示，混凝土顶底板的纵向应变εf为

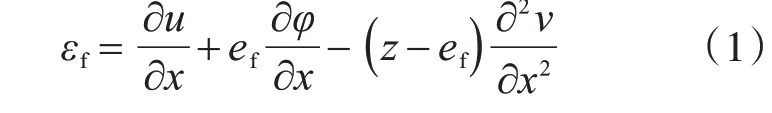
式中：u 为梁截面形心轴的纵向位移；ef为顶板或底板自身形心轴的z轴坐标值；φ为截面转角；v为梁挠度值。

由图4 可知，波形钢腹板剪应变γw可以表示为

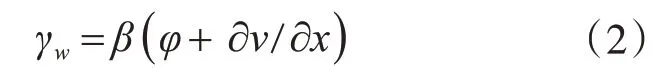
式中：β=h/hw；h 为顶底板自身形心轴之间的距离；hw为腹板高度（图2）。

根据竖向力平衡可以得到

式中：V为截面上的总剪力；q为竖向分布力。

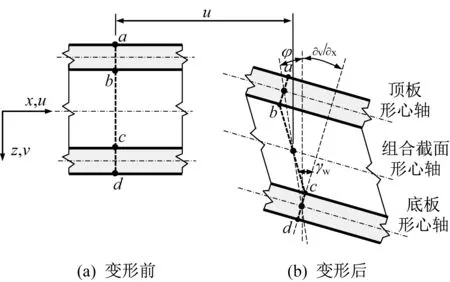
图4 梁节段变形Fig.4 Deformation of a beam segment

作用在截面上的总剪力由两部分构成：①顶底板承担的与顶底板绕各自形心轴局部弯曲相对应的剪力，即式（4）右侧第一项；②组合截面承担的与绕组合截面形心轴整体弯曲相对应的剪力，此时假设顶底板不发生绕各自形心轴的局部弯曲，即式（4）右侧第二项。

式中：Bf为顶底板相对于自身形心轴的局部弯曲刚度；为波形钢腹板的剪切刚度；Gw为腹板钢材剪切模量；bw为腹板总厚度；s及s0分别为波形腹板半波范围的实际与投影长度（图2（b））。

根据弯矩平衡条件，可以得到

作用在截面上的总弯矩M 可以通过对截面上的正应力进行积分得到，即

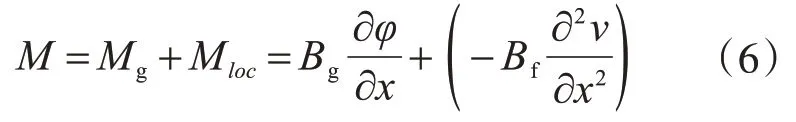
式中，Bg为围绕组合截面形心的整体弯曲刚度，此时假设顶底板不发生绕各自形心轴的局部弯曲（即应变沿顶底板厚度方向不变）。

式（6）右侧第一项为绕整个截面形心的整体弯矩，即Mg=Bg(∂φ/∂x)；第二项为顶底板围绕各自形心轴的局部弯矩之和Mloc，即Mloc=-Bf(∂2v/∂x2)。

将式（4）及式（6）代入式（3）及式（5），并进行重新整理后可得到

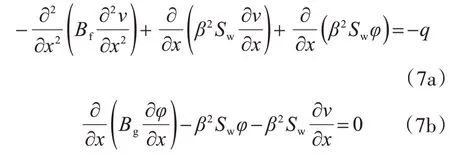
由上述两式消去参数φ 及其导数，可以得到由挠度v及其导数表达的梁段微分控制方程

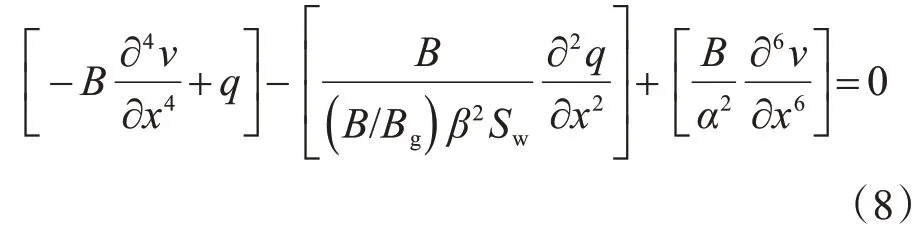
式中，α2=

以上控制方程与学者Mead 和Markus［18］推导的传统夹层梁模型基本一致，但是截面特性的表达式不同。式（8）左侧第一个方括号内的项为不考虑剪切变形的梁体弯曲最基本情况，即欧拉梁理论。其第二个括号内的项由剪切变形引起。当腹板剪切刚度很大时，该项就可忽略不计。联合第一个与第二个方括号内的项即为铁木辛柯梁理论。第三个方括号内的项由混凝土顶底板局部弯曲与腹板剪切变形的耦合作用引起。当腹板剪切刚度无穷大时，该项也可忽略不计。参数α 为衡量上述耦合作用的关键参数，其为组合截面等效剪切刚度（B/Bg）β2Sw与顶底板局部弯曲刚度Bf比值的平方根。参数α越小，该耦合作用越显著。

以一个波形钢腹板组合简支梁为例，在跨中集中力作用下其剪切变形如图5 所示。假设忽略混凝土顶底板的局部弯曲，在集中力附近出现变形不协调，如图5（a）所示。实际上，在集中力作用处，混凝土顶底板不可能出现无穷大的曲率，而是发生连续光滑的局部弯曲，如图5（a）的粗虚线所示，从而引起混凝土局部弯曲与波形钢腹板剪切变形的耦合，最终的整体剪切变形如图5（b）所示。

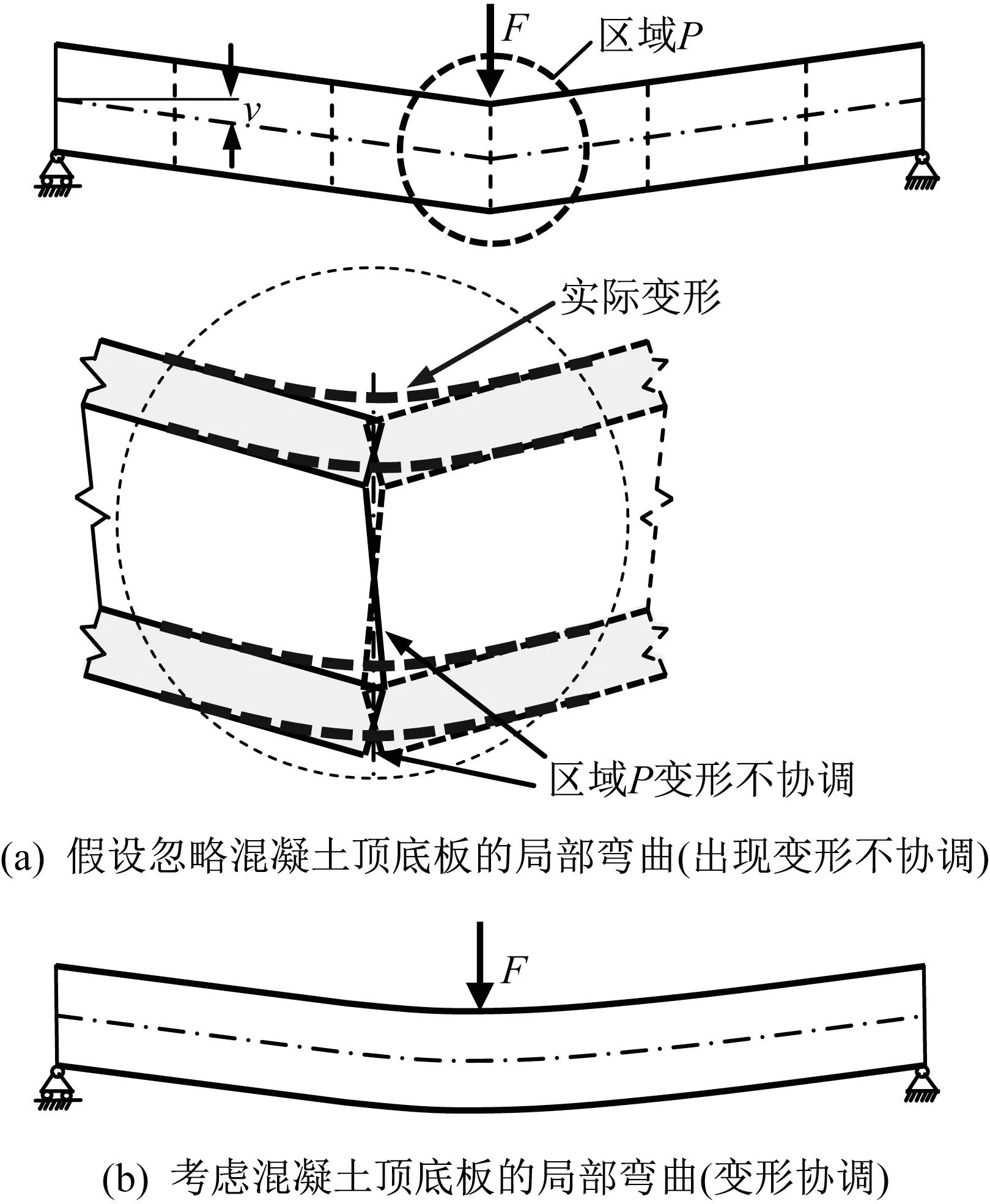
图5 波形钢腹板组合简支梁在跨中集中力作用下的剪切变形Fig.5 Shear deflection of a simply supported bridge under a point load at mid span

实际上，当剪力沿跨径方向变化时，都会发生上述耦合作用，例如均布荷载作用工况。但是，在均布荷载作用下，剪力变化连续，耦合作用不显著。

1.2 横隔板作用

该类桥梁通常设置横隔板。因为波形钢腹板的轴向刚度很小，同时其剪切变形又比较显著，因此横隔板会通过约束波形腹板的剪切变形及顶底板的相对位移对结构的受力性能产生显著的影响，如图6所示。

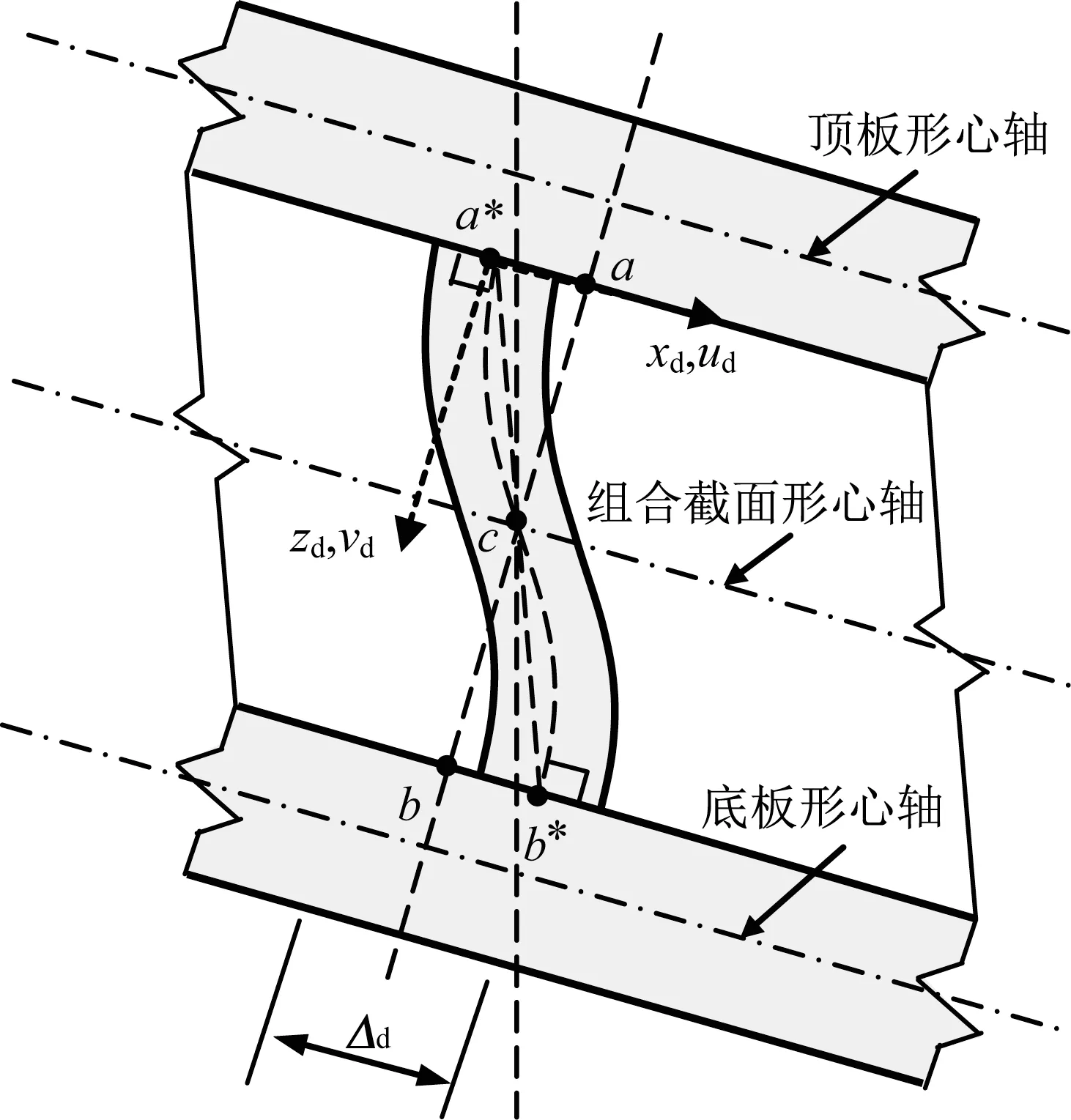
图6 横隔板附近剪切变形Fig.6 Shear deformation in the vicinity of a diaphragm

横隔板将梁分成一个个梁段。在每个横隔板位置处，梁段都必须满足力的平衡和变形协调条件。假设横隔板与顶底板和腹板均连接。由于横隔板的作用，在横隔板邻近区域波形钢腹板发生扭曲，剪切变形沿腹板高度不再一致。原来位于同一平面上的腹板截面a-c-b 扭曲成曲面a*-c-b*。同时与横隔板相连接的顶底板位置发生相对位移Δd。在横隔板位置处的变形协调条件可以表示为

在横隔板位置处的力的平衡条件可以表示为

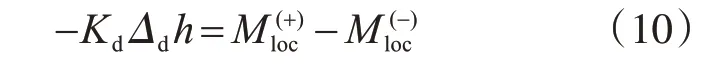
或

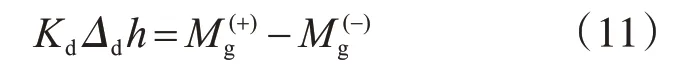
式中，Kd为横隔板约束顶底板相对位移的刚度。

联立变形协调条件方程式（9）与力的平衡方程（11），得到横隔板位移需要满足的附加条件为

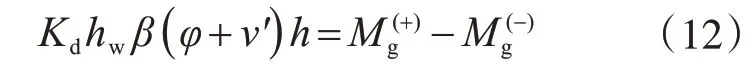
如果横隔板与腹板不连接，式（12）也同样适用。

如果横隔板很厚，可以将横隔板当作一个沿桥跨径方向的梁段。

在本质上，横隔板的作用是顶底板局部弯曲与腹板剪切变形耦合作用的一种特例。

2 有限元梁单元

为了方便进行实际工程设计计算，本文基于建立的夹层梁模型，提出一种有限元梁单元。

2.1 梁单元

提出的三节点梁单元（C1阶连续）如图7所示。

该三节点梁单元的位移向量d 由梁轴心纵向位移u、挠度v 以及转角φ 组成，分别采用线性、三次Hermite以及二次多项式插值函数，即

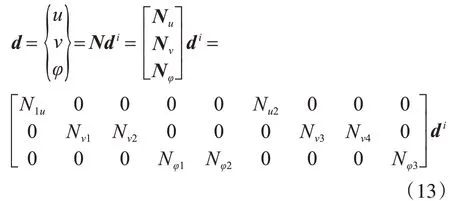
式中：梁单元节点位移向量

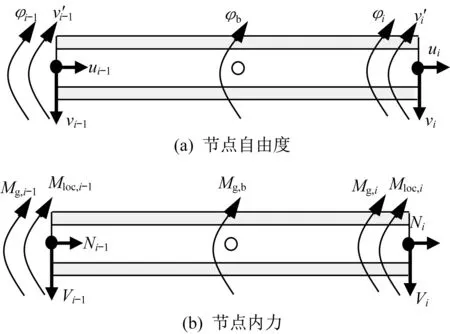
图7 三节点C1梁单元Fig.7 A C1 three-node beam finite element

di={ui-1vi-1v′i-1φi-1φibuiviv′iφi}T；形函数矩阵N包含子形函数矩阵Nu、Nv及Nφ；Nu1=1-ξ；Nu2=ξ；Nv1=1-3ξ2+2ξ3；Nv2=(ξ-2ξ2+ξ3)Li；Nv3=3ξ2-2ξ3；Nv4=(-ξ2+ξ3)Li；Nφ1=1-3ξ+2ξ2；Nφ2=4ξ-4ξ2；Nφ3=-ξ+2ξ2；(0≤ξ ≤1)；以及Li为第i 个单元的长度。

第i个单元的应变能Uib为

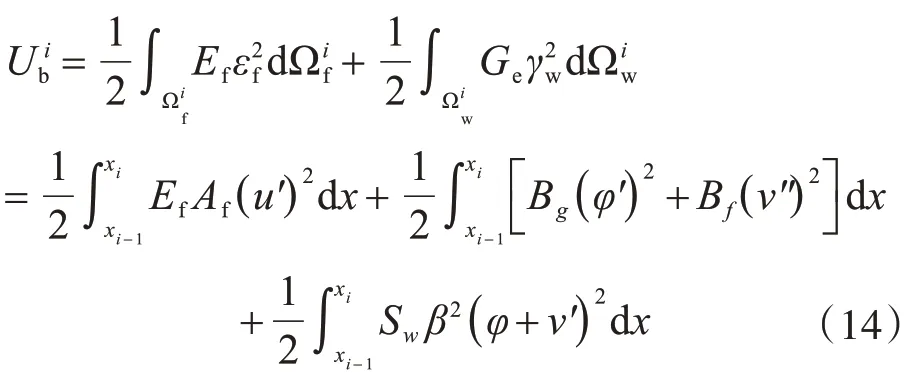
将式（13）中各变量的表达式代入式（14）可以得到

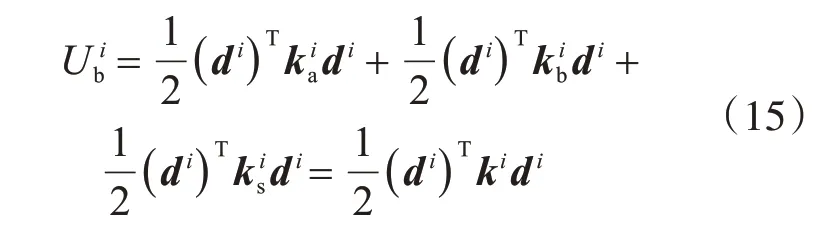
式中：kia为单元的轴向刚度矩阵；kib为单元的弯曲刚度矩阵；kis为单元的剪切刚度矩阵；ki为单元的总刚度矩阵，即ki=kia+kib+kis。

这些刚度矩阵的表达式为

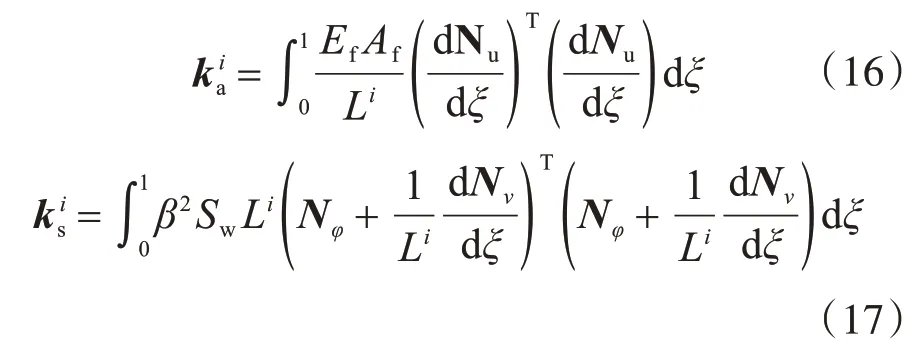
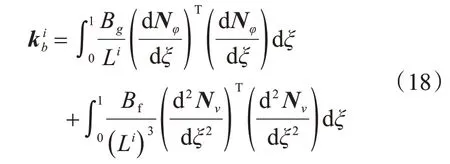
2.2 横隔板作用的模拟

在划分梁单元时，在横隔板位置布置为端节点。第k 个横隔板的作用可以用一对值为Kdhwβ(φ+v′)h的内力偶（见式（12））模拟，其引起的应变能Udia，k为

式中，xk为第k 个横隔板位于x 轴方向的位置；dk为端节点的位移向量；kdia，k为由第k个横隔板提供的附加刚度，其可以表示为

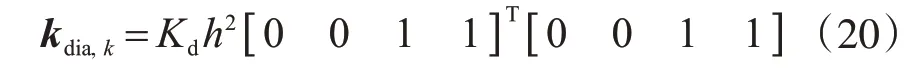
如果横隔板较厚，也可以将横隔板当作沿桥纵向的梁单元，并将实心截面划分成虚拟的顶底板与腹板，并计算它们的弯曲及剪切刚度等截面特性，以保证与夹层梁单元连接时的协调相容。

2.3 结构体系的模拟

由梁体与横隔板组成的整个结构体系的总势能为

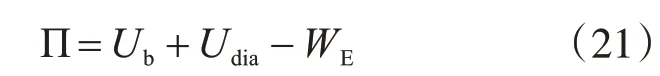
式中：Ub为梁体的总应变能；Udia为横隔板引起的总应变能；WE为外力作用f的势能，其表达式为

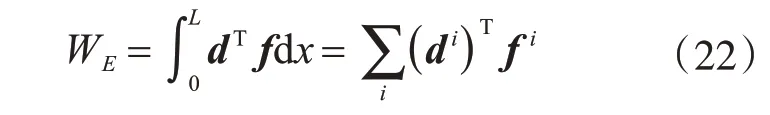
式中，外力作用f包含轴向分布力p 以及横向分布力q，即f =[p q 0]T以及

根据最小势能原理，可以得到

根据常规的有限元方法推导步骤，可以得到有限元的公式为

3 试验验证

本部分通过试验对所提出的夹层梁理论进行验证。其中的3 个试件A-1、B-1 及B-2 分别如图8-图10 所示。试件A-1 总长4 700 mm，跨径4 500 mm，高300mm，波形钢腹板厚5 mm。试件B-1及B-2总长3 800 mm，跨径3 600 mm，高360 mm，波形钢腹板厚5 mm。波形钢腹板与混凝土顶底板之间采用埋入式连接件。

每个试件均施加两根直径12.7 mm 的体外预应力钢绞线。试件A-1 预应力筋采用折线形布置，钢绞线锚固于端横隔板中心线位置，在中横隔板位置的转向孔距梁底70 mm。试件B-1 预应力筋采用直线形布置，预应力钢绞线锚固于端横隔板距梁底110 mm 处。试件B-2 预应力筋采用折线形布置，钢绞线锚固于端横隔板中心线位置，在中横隔板位置的转向孔距梁底100 mm。施加在试件A-1、B-1及B-2的有效总预应力分别为191 kN、268 kN及252 kN。

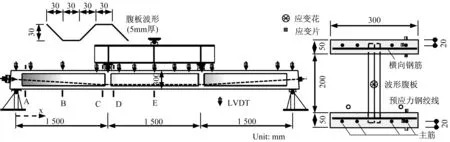
图8 试件A-1Fig.8 Configuration of Specimen A-1

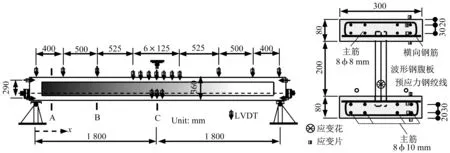
图9 试件B-1Fig.9 Configuration of Specimen B-1

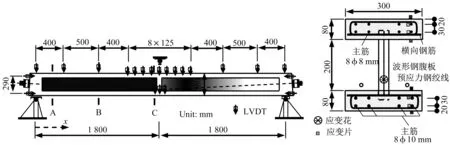
图10 试件B-2Fig.10 Configuration of Specimen B-2

试件的材料特性如表1、表2所示。

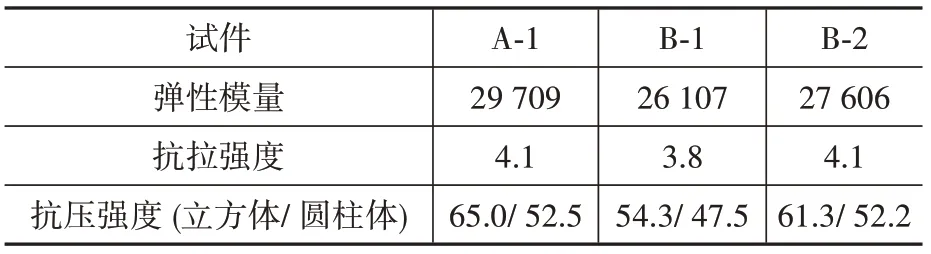
表1 试件混凝土材料性能Table 1 Material properties of concrete from tests（MPa）

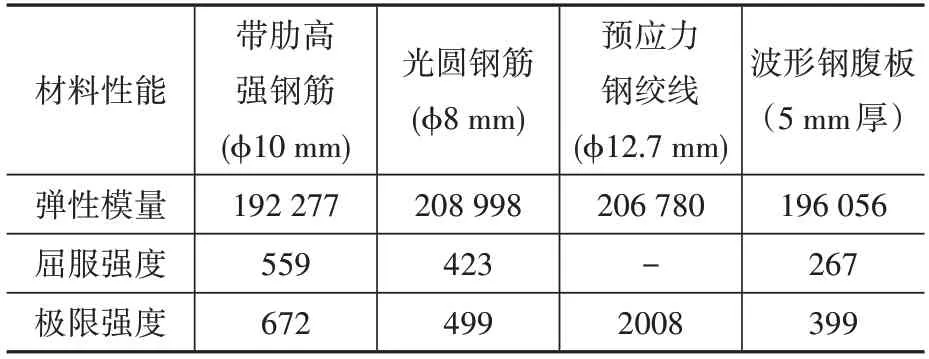
表2 试件钢筋、预应力筋及波形腹板材料性能Table 2 Material properties of steel reinforcing bar，prestresing steel，and steel web from tests (MPa)

分别对试件A-1、B-1、B-2 进行静力加载试验，如图11所示。

图11 静力加载Fig.11 Static loading test

试验结果如图12—图16所示，并与建立的夹层（Sandwich）梁理论、传统的铁木辛柯（Timoshenko）梁理论、及欧拉（Euler）梁理论结果进行比较。如图12 所示，应用铁木辛柯梁理论得到的挠度大于试验值，因为该理论未考虑顶底板局部弯曲与腹板剪切变形的耦合作用以及横隔板作用；应用欧拉梁理论得到的挠度小于试验值，因为其未考虑剪切变形。如图13 所示，由于上述耦合和横隔板作用，波形钢腹板的剪应力在横隔板与集中力位置附近急剧地减小，相对应的混凝土顶底板承担的剪力在这些位置急剧地增加。如图14—图16 所示，在横隔板及集中力附近正应力沿截面高度线性分布的假定不适用，例如试件A-1的截面A 与C，试件B-1 与B-2 的截面A 与C。而在远离横隔板及集中力的位置，正应力沿截面高度线性分布的假定是适用的，例如试件A-1 的截面B 与E，试件B-1 与B-2 的截面B。夹层梁理论结果与试验结果基本吻合，验证了所提出的夹层梁理论模型的可靠性。

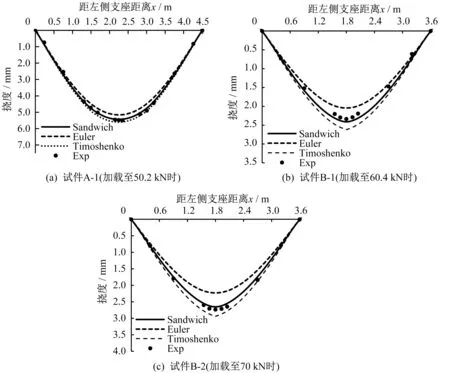
图12 试件挠度Fig.12 Deflection of specimens tested

理论与试验结果存在细微差异的主要原因可能是理论推导过程中采用了以下假设：①混凝土顶底板与波形腹板的连接是理想的，无滑移；②混凝土顶底板的剪切变形可忽略不计；③波形钢腹板沿桥纵向的轴向刚度可忽略不计。因此，在使用该理论进行分析计算时，需要注意以下对应的应用条件：①若结构可能发生明显剪切滑移，则须根据剪力连接件的类型引入合适的剪切-滑移关系；②梁跨径与混凝土翼板厚度的比值宜大于10；③实际工程中，波形钢腹板沿桥纵向的轴向刚度通常可忽略不计。如果波形钢腹板的波形参数比较特殊，须核算其轴向刚度是否可以忽略（小于相同厚度平钢腹板轴向刚度的1%可忽略不计）［19-20］。

当结构处于弹性阶段，夹层梁理论的假设都基本成立，引起的误差可以忽略。在实际工程设计时，可以应用该理论验算结构正常使用极限状态的应力与变形。该理论也可以清晰地计算出组合截面的混凝土翼板与波形钢腹板各自承担的剪力比例，以便进行承载能力极限状态下抗剪强度的验算。当结构处于塑性状态，为了准确计算该类桥梁的抗弯承载力，还需要基于推导的夹层梁理论，进一步引入材料非线性本构关系、剪切-滑移关系、几何非线性方程、体外预应力与梁体耦合作用方程等。

4 结 论

图13 腹板中间高度位置剪应力Fig.13 Shear stresses at mid-height of the web

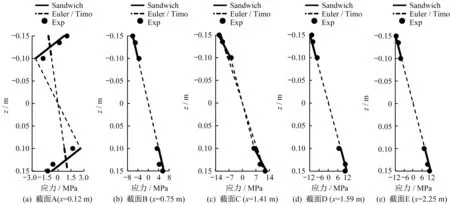
图14 试件A-1截面正应力（加载至50.2 kN时）Fig.14 Normal stress distribution of Specimen A-1（loading 50.2 kN）

本文提出了一种适用于波形钢腹板组合桥梁的夹层梁理论模型，以分析该类桥梁的弯曲与剪切性能。该模型考虑了混凝土顶底板局部弯曲与波形腹板剪切变形的耦合作用以及横隔板作用。应用试验验证了该理论模型的可靠性。研究表明总体上正应力沿截面高度线性分布的假设对于该类桥梁是成立的，但是由于顶底板局部弯曲与波形腹板剪切变形的耦合及横隔板作用，在集中力与横隔板附近的混凝土顶底板会出现显著的剪应力与正应力集中，并导致正应力沿截面高度线性分布的假设局部不成立。由于上述耦合和横隔板作用，波形钢腹板承担剪力的比例在集中力与横隔板附近急剧地减小，相对应地混凝土顶底板承担剪力的比例在这些位置急剧地增加。

在设计该类桥梁时，需要注意在集中力位置（例如支撑位置）及横隔板位置附近的混凝土顶底板内应力集中的问题，建议通过设置加腋减轻上述应力集中。

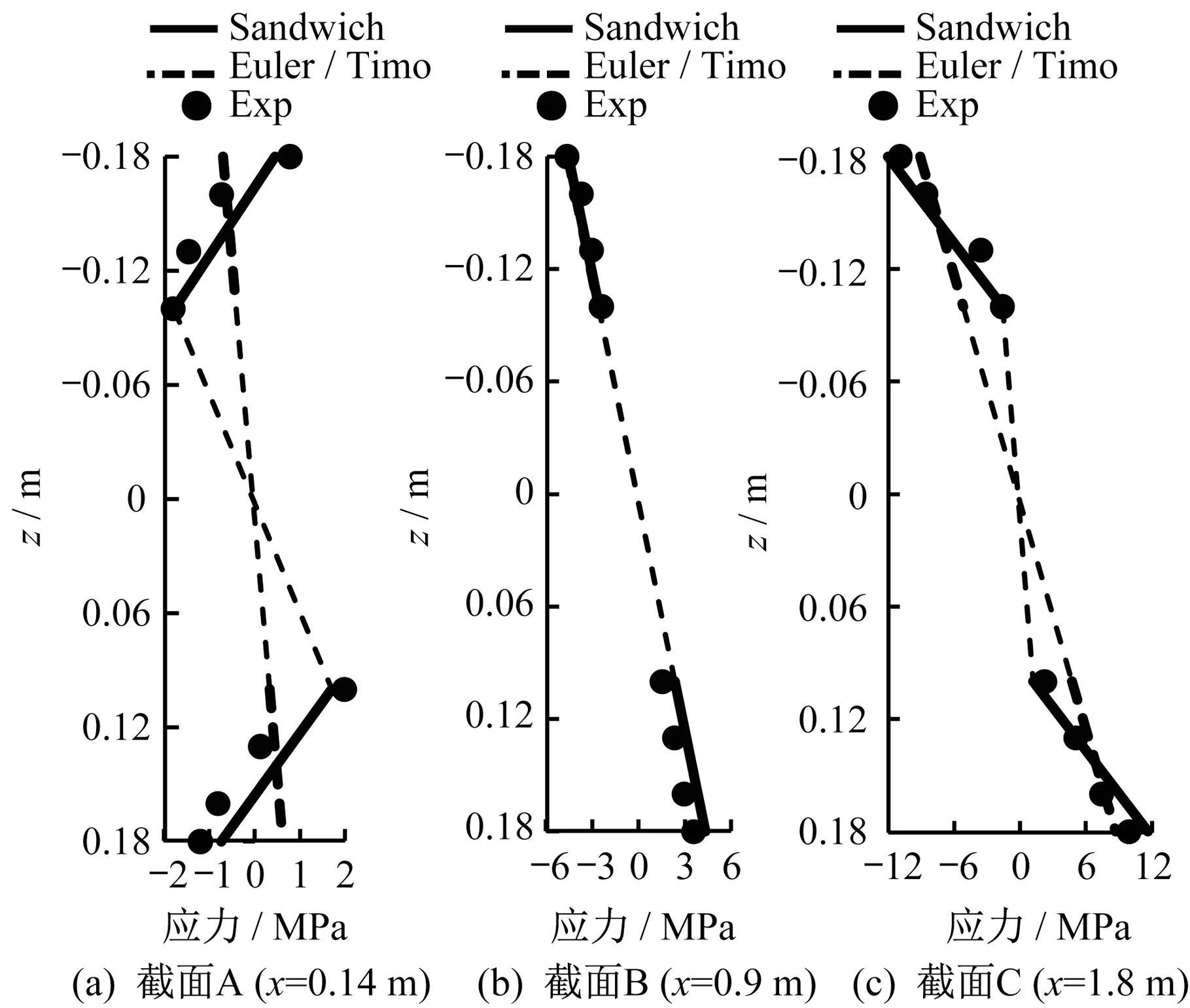
图15 试件B-1截面正应力（加载至60.4 kN时）Fig.15 Normal stress distribution of Specimen B-1（loading 60.4 kN）

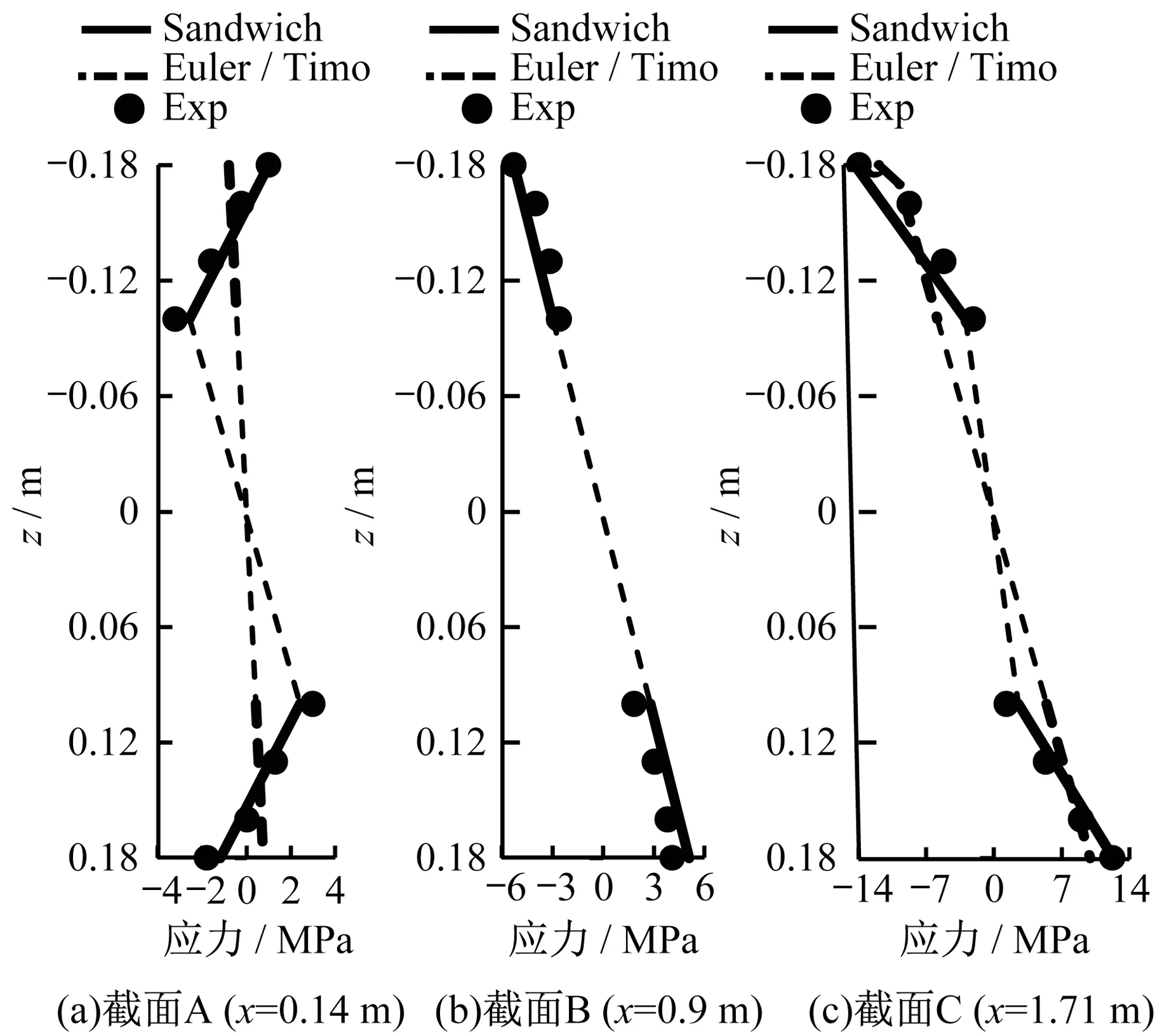
图16 试件B-2截面正应力（加载至70 kN时）Fig.16 Normal stress distribution of Specimen B-2（loading to 70 kN）