某体育馆张弦梁结构屋盖设计

朱 奇 姚开明 戚向明

（浙江绿城建筑设计有限公司，杭州310007）

0 引 言

张弦梁结构是一种半刚性结构，其通过在下弦杆施加初张力让上弦杆产生反拱，从而减小荷载作用下结构的挠度；同时上下弦杆之间的撑杆相当于上弦杆的弹性支撑，使得上弦杆的弯矩较小。此外上弦与下弦杆的轴力是一对平衡的力，不会对支座产生额外的水平推力，整个结构形成了一个自平衡体系［1］。张弦梁面外的稳定性通过屋面檩条和纵向支撑构件来保证［2］。

图1 张弦梁结构Fig.1 Beam string structure

1 工程概况

某学校体育馆上方屋盖采用张弦梁结构，主体钢结构共包括7 榀张弦梁，跨度32.8 m，柱距8.4 m，为提高屋面整体稳定性，上弦平面设置水平系杆。张弦梁为双钢管梁单索体系，上弦为φ245 mm×18 mm 的弧形双钢管梁，下弦设置一根LS-ZnAl-1670-7.0-55 的平行钢丝束，撑杆尺寸102×6，除拉索外，其他钢构件均采用Q355B 级钢。张弦梁结构平面和立面如图2 所示，计算模型如图3所示。

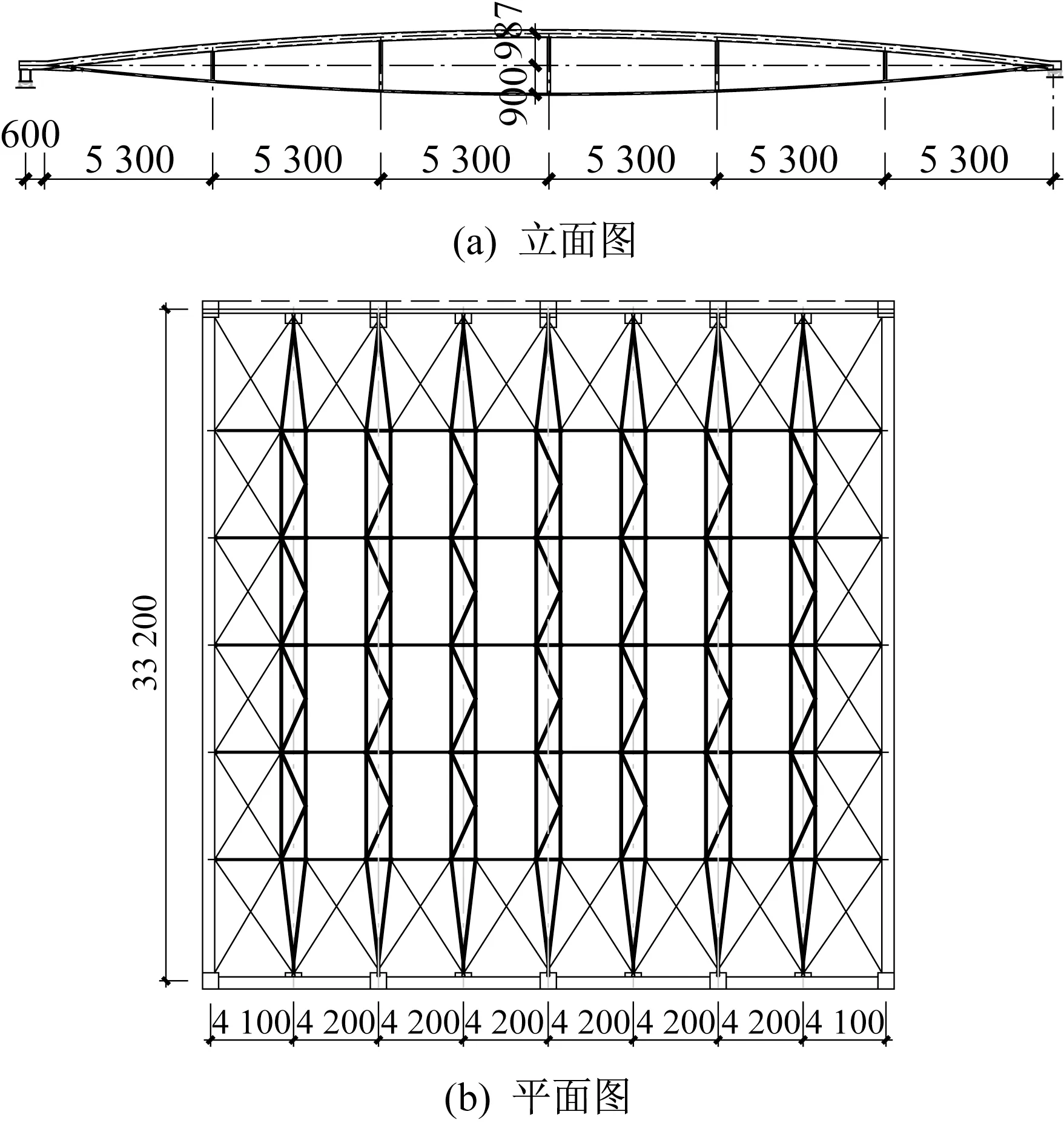
图2 张弦梁结构布置图（单位：mm）Fig.2 Layout of beam string structure（Unit：mm）

图3 计算模型Fig.3 Calculation model

2 理论分析

2.1 张弦梁曲线确定

确定合理的张弦梁曲线是结构建模计算的第一步，国内许多工程均采用迭代法进行预应力张弦梁结构的形态分析及张拉力的确定［3-5］。本文通过理论推导得到张弦梁的曲线形状和初张力。

屋面结构在自重和屋面恒载作用下结构会下挠，通过在下弦中施加预应力，使得上弦杆产生反拱，合理的张弦梁曲线可以使得二者变形正好抵消让结构张拉完成后，恒载作用下基本没有变形。

截取半边张弦梁结构进行分析，如图4 所示。张弦梁跨中矢高为h3+ h5，张弦梁的跨度L为2（L1+L2+L3），下弦杆的初张力为T。

图4 半跨张弦梁分析示意图Fig.4 Schematic diagram of half-span beam string structure

上下弦杆采用折线，在转折点位置左右弦杆内力的合力均会产生向上的分力，该分力提供上弦杆的支承力。为使得上弦杆在撑杆位置竖向位移为0，该支承力需等于等效多跨连续梁（受均布荷载，上下弦杆承担的均布荷载为q2、q1）在此处的支座反力。选取撑杆1位置进行分析。

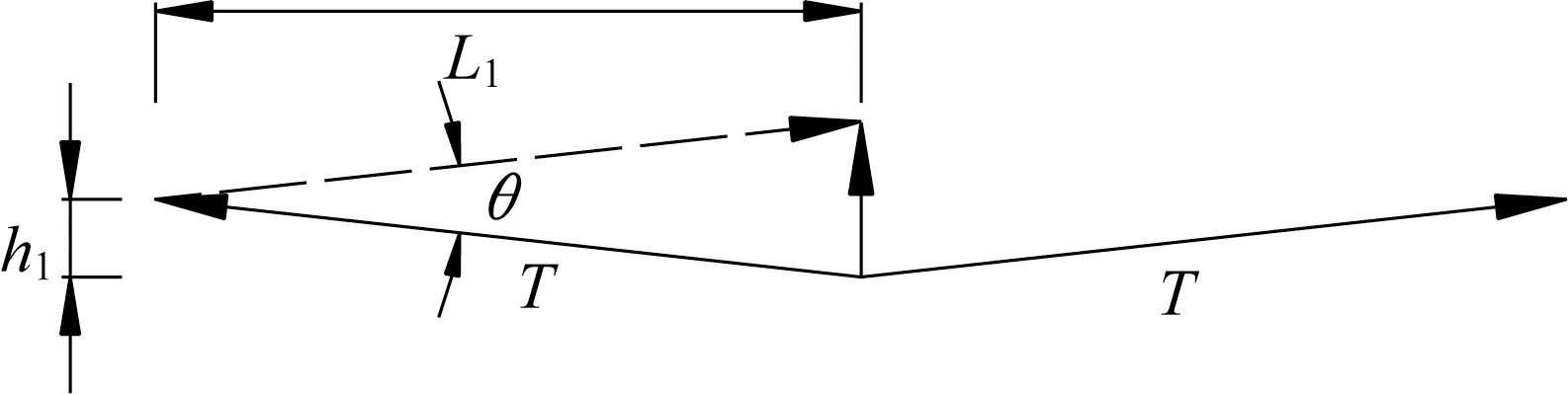
图5 撑杆1位置受力分析Fig.5 Force analysis at position of bracing 1

对于一般情况，张弦梁的跨度远大于张弦梁跨中的矢高，则h1＜＜L1，因而可以近似的认为：

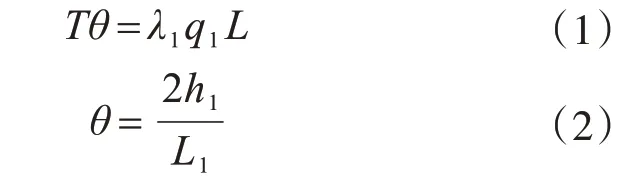
式中，λ1为等效多跨连续梁相应支座的反力系数。

根据式（1）、式（2）可得：

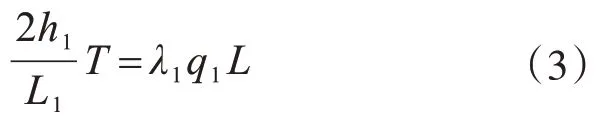
同理对于撑杆2、撑杆3位置进行分析可得：

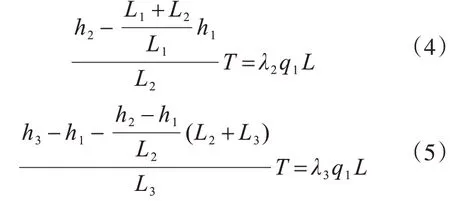
式中，λ2、λ3含义与λ1类似。

结合式（3）、式（4）、式（5）可得：

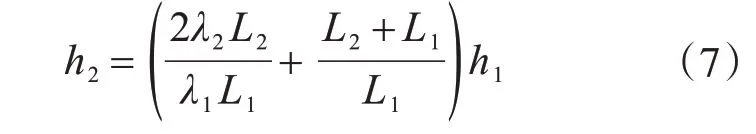
根据式（6）、式（7）即可得到下弦杆的曲线形状，同理对上弦杆进行类似分析得到上弦杆的曲线形状。对于其他跨数分布的张弦梁亦可类似分析得到合理的张弦梁曲线形状。

2.2 初张力确定

对撑杆1位置上弦杆进行类似分析可得：

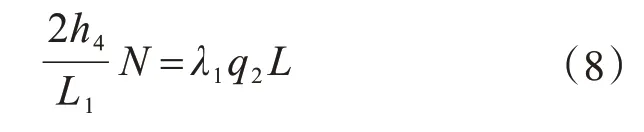
由于上下弦杆的轴力是一对平衡，则有N=T，结合式（3）可得：

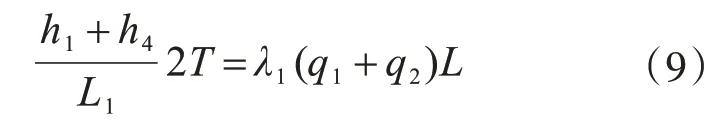
令Q=q2+q1（等效连续梁的均布荷载），可得：

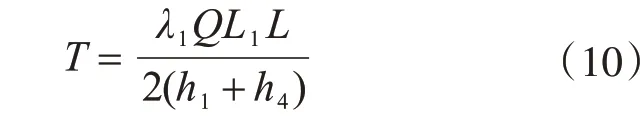
根据式（10）可以得到下弦杆的初张力。表1给出了几种常见腹杆分布情况下的h1、h2、λ1的数值，根据表1 即可得出相应的张弦梁曲线和预张力。

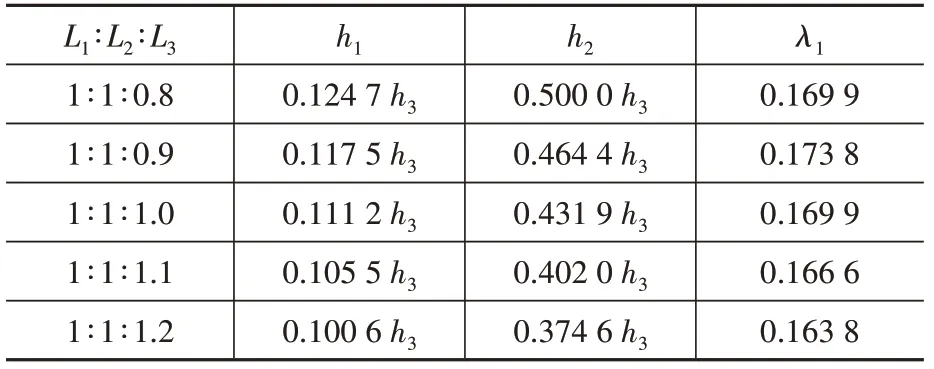
表1 常见腹杆分布的h1、h2、λ1Table 1 h1，h2，λ1 Values for common distributions of web members

2.3 误差分析

进一步验证理论分析结果，采用SAP2000 进行模型分析。模型中上弦杆、腹杆采用Q345的钢管。对下弦杆采用降温法进行张拉，张拉完成后腹杆1 位置竖向位移为0，腹杆2、腹杆3 位置竖向位移Δ2、Δ3，软件计算得到初张力为T1，根据式（10）理论计算得到初张力为T0，结果对比如表2所示。

表2 SAP2000计算结果与理论解对比Table 2 Comparison between SAP2000 results and theoretical solutions

根据表3 可知，不同跨度的张弦梁SAP2000的计算结果与根据式（10）求出的初张力结果相比误差在5%以内，且腹杆处的位移很小，说明上述理论推导求解得出的结果是符合真实情况的，能够满足一般工程的需要。

3 计算结果分析

根据上述理论分析得到的张弦梁的曲线建立整体分析模型，进行结构计算设计。根据上述公式（10）计算得到该张弦梁的预张力为385 kN，经SAP2000 计算得到的预张力为392.7 kN，二者相差1.85%。

3.1 屈曲分析

由于本屋盖较轻，在风吸荷载作用下，张弦梁的下弦拉杆可能会受压而退出工作，经计算得到结构在满跨均布风吸荷载标准值作用下的弹性屈曲因子为1.93，屈曲模态为下弦杆的压曲，如图6所示。结构在半跨均布风吸荷载标准值作用下的弹性屈曲因子为3.54，屈曲模态为下弦杆的压曲，如图7 所示，该结构对于半跨风吸荷载作用不敏感。

图6 满跨均布风吸荷载作用下的弹性屈曲Fig.6 Elastic buckling under full-span uniform wind suction load

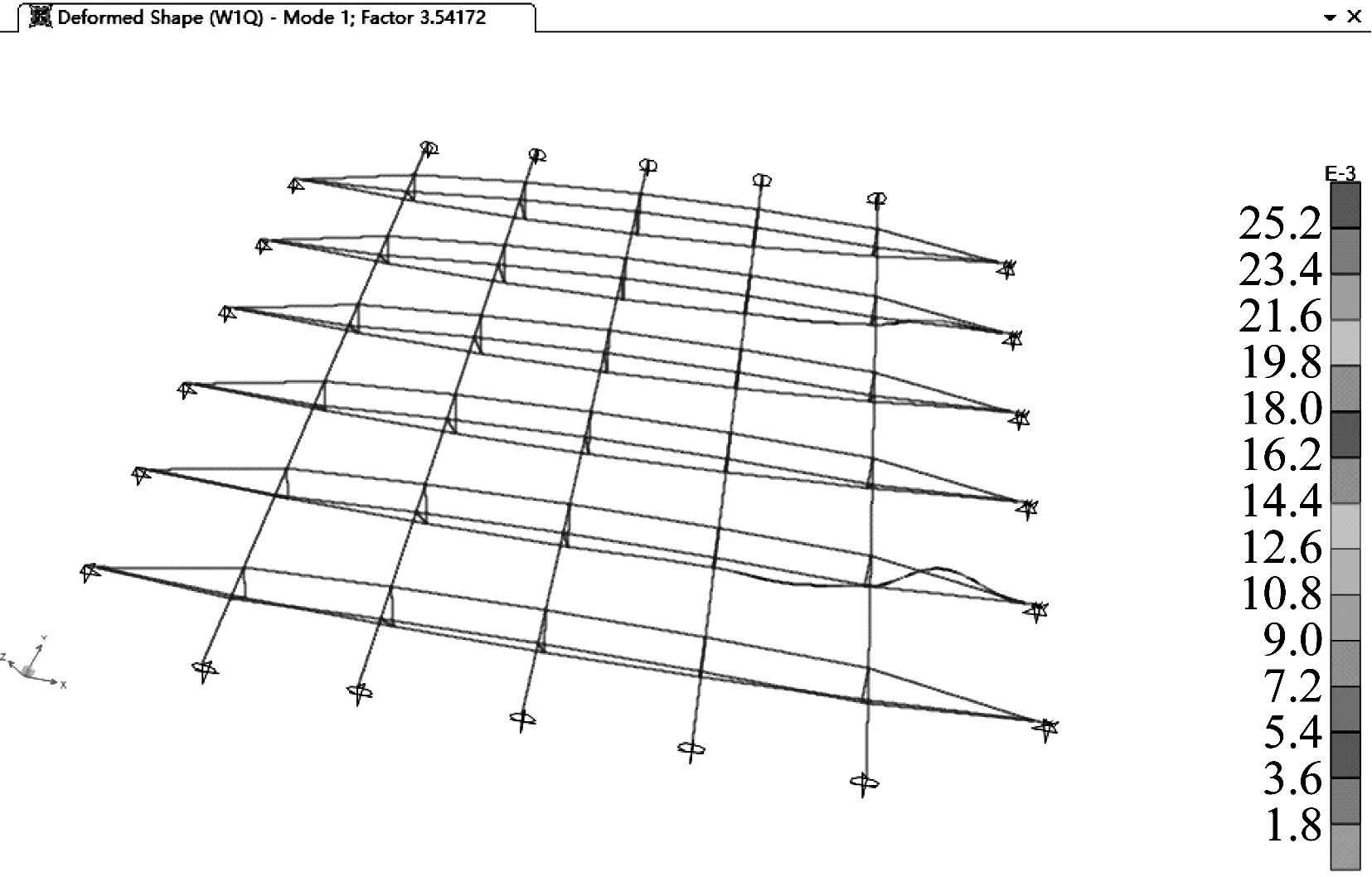
图7 半跨均布风吸荷载作用下的弹性屈曲Fig.7 Elastic buckling under half-span uniform wind suction load

上弦杆在平面内由腹杆提供支撑，平面外由横向系杆提供支撑，屋面为不上人屋面活荷载较小。因此上弦杆在活荷载作用下弹性屈曲因子较大，经过计算得到上弦杆在满跨均布活载作用下的弹性屈曲因子为61.8，屈曲模态为上弦杆的压曲，屈曲模态如图8 所示。上弦杆在半跨均布活载作用下的弹性屈曲因子为69.3，屈曲模态为上弦杆的侧向压曲，屈曲模态如图9所示。

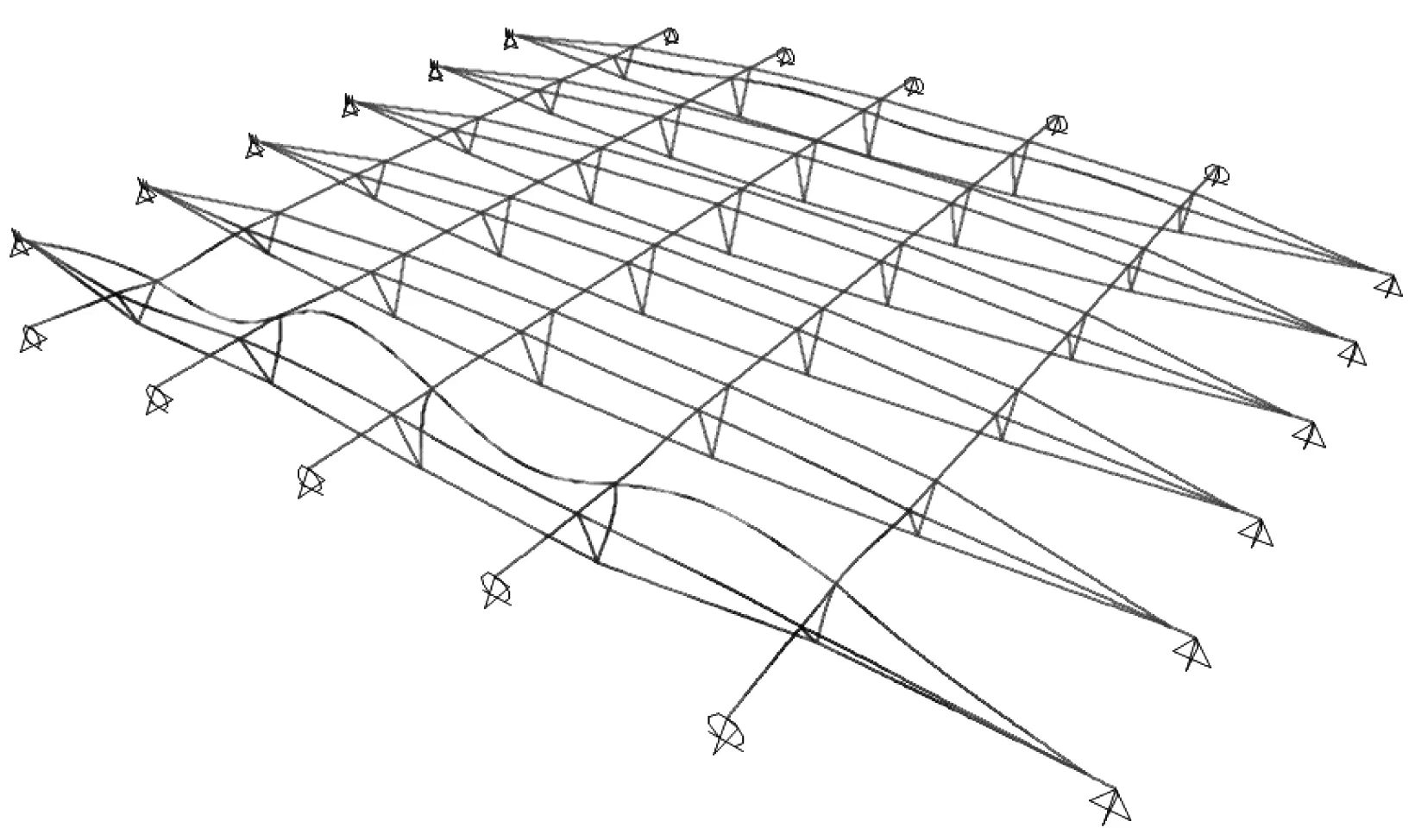
图8 满布活荷载作用下的弹性屈曲Fig.8 Elastic buckling under full-span uniform live load

3.2 极限承载力分析

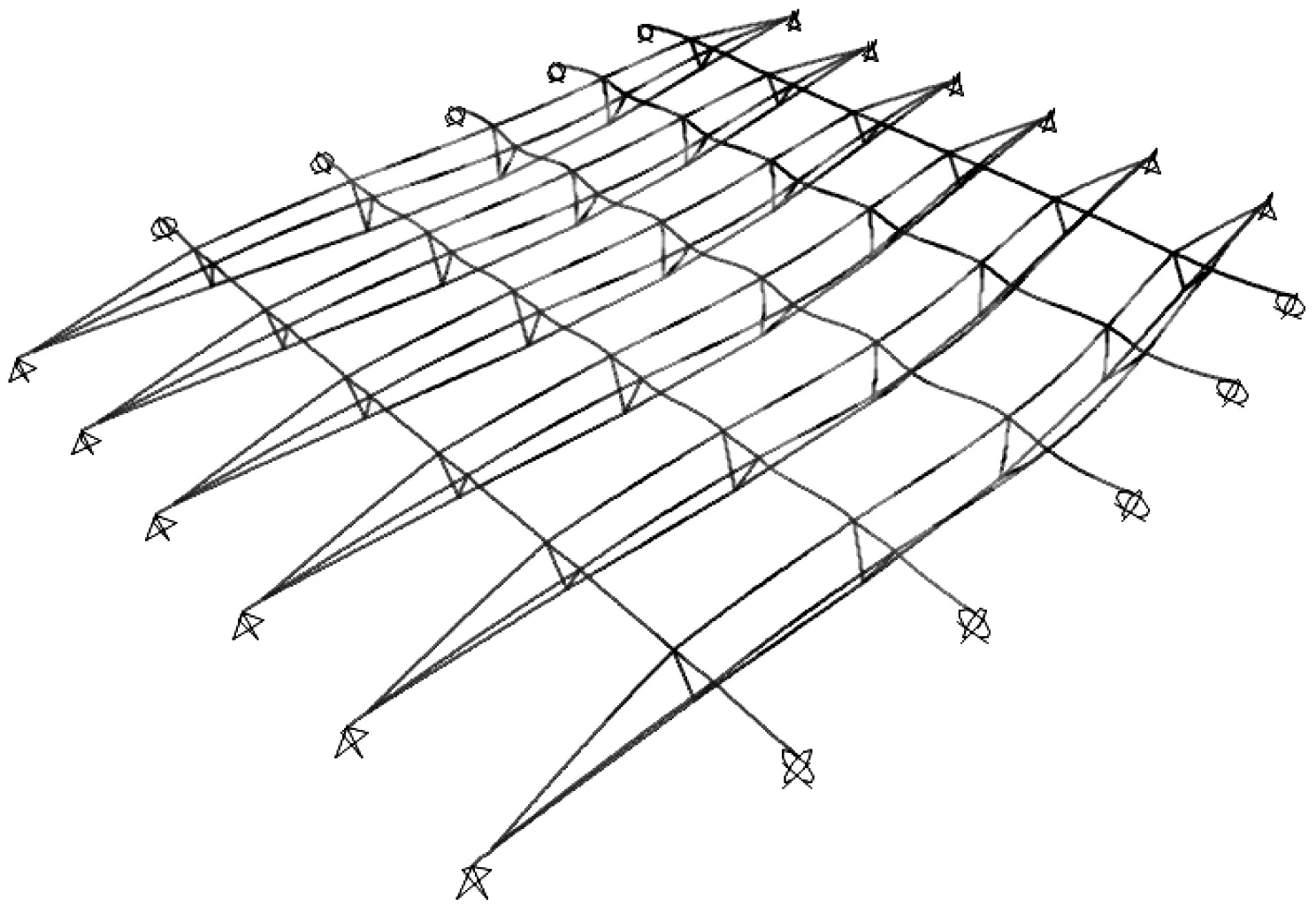
图9 半跨活荷载作用下的弹性屈曲Fig.9 Elastic buckling under half-span uniform live load

本工程张弦梁两端采用球形钢支座与主体结构相连，一端为固定支座，一端为滑动支座。为了防止张弦梁跌落需要对滑动端的位移进行限制。分析表明结构在初始状态进行初张拉后，张弦梁上弦杆中弯矩较小（如图10 所示，最大弯矩43 kN·m），张弦梁滑动端的水平位移仅为-2 mm。结构在恒载+1.5倍满布风吸荷载标准值作用下滑动端水平位移为-17 mm。结构在1.3 倍恒载+1.5倍满布活载作用下，支座的水平位移为13 mm。综合考虑滑动端水平位移限值为±50 mm。

图10 初张拉后上弦杆弯矩图Fig.10 Bending moment of top chord after initial stretching

为了研究整个结构的极限承载力，需要对结构进行荷载-位移全过程跟踪分析。对于支座的模拟采用SAP2000 中的hook 连接单元，该单元的非线性力-变形关系如下：

式中：k为弹簧常数；open为初始缝宽。

张弦梁结构在风吸荷载作用下，各弦杆的轴力-荷载曲线如图11所示，张弦梁滑动端的荷载-位移曲线如图12 所示，支座水平反力如图13 所示，上弦杆中弯矩如图14所示。

结合图11、图12 可知，在0-A 阶段，滑动端支座的水平位移逐渐增大，两根上弦杆合力逐渐减小，下弦杆拉力减小，三者成线性关系。在1.6 倍风吸荷载标准值作用下，下弦杆拉力减为0 而退出工作，此时竖向的恒载正好与风吸荷载抵消。在1.0倍风吸荷载标准值作用下，张弦梁的跨中竖向向上位移为0.070 m（1/460）。

在A-B 阶段，滑动端的位移逐渐增加至其限制位移50mm，此过程上弦杆的合轴力变化不大，主要靠上弦杆受弯来承受增加的风荷载，如图14所示。

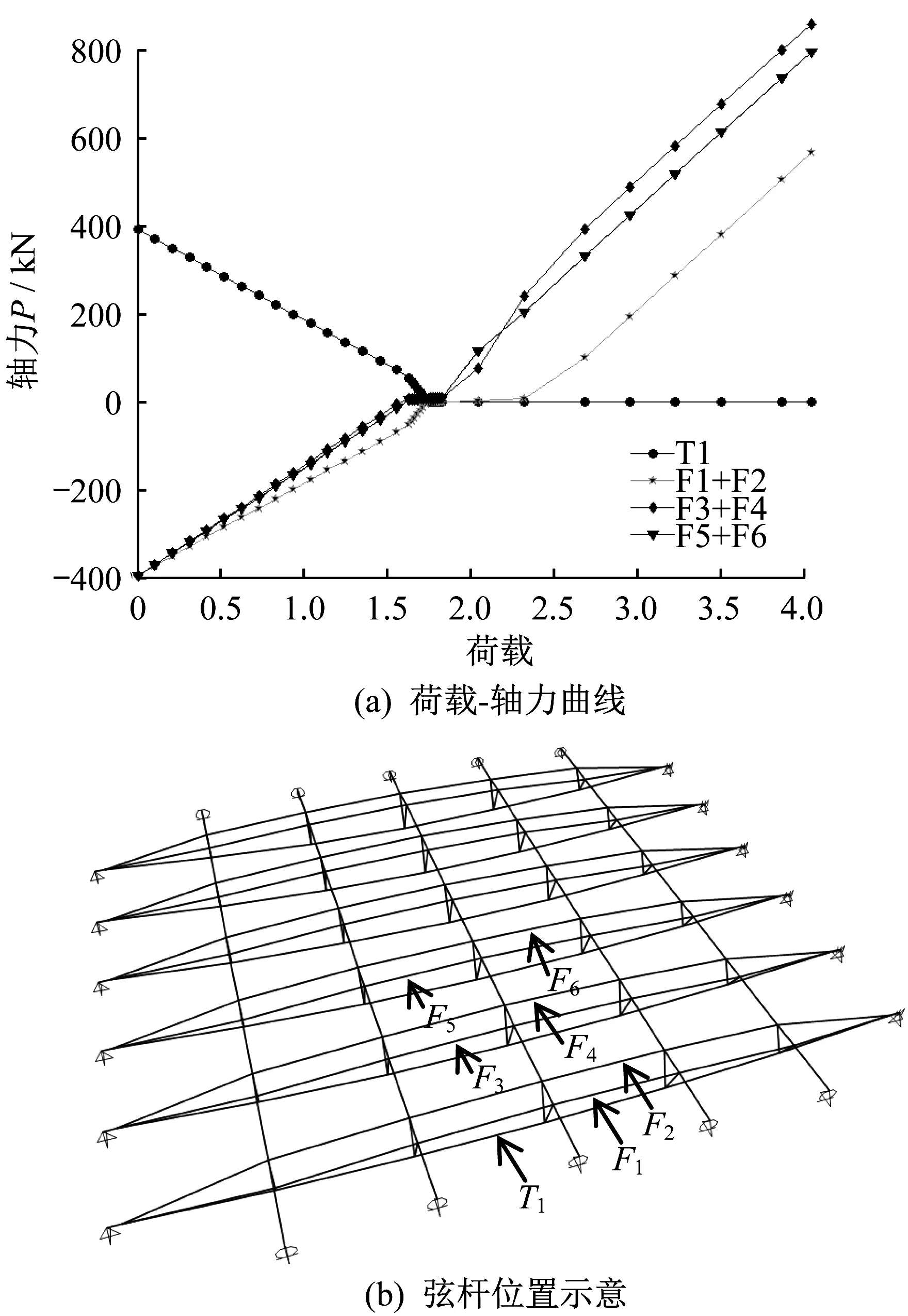
图11 风吸荷载作用下荷载-轴力曲线Fig.11 Load-axial force curve under wind suction load

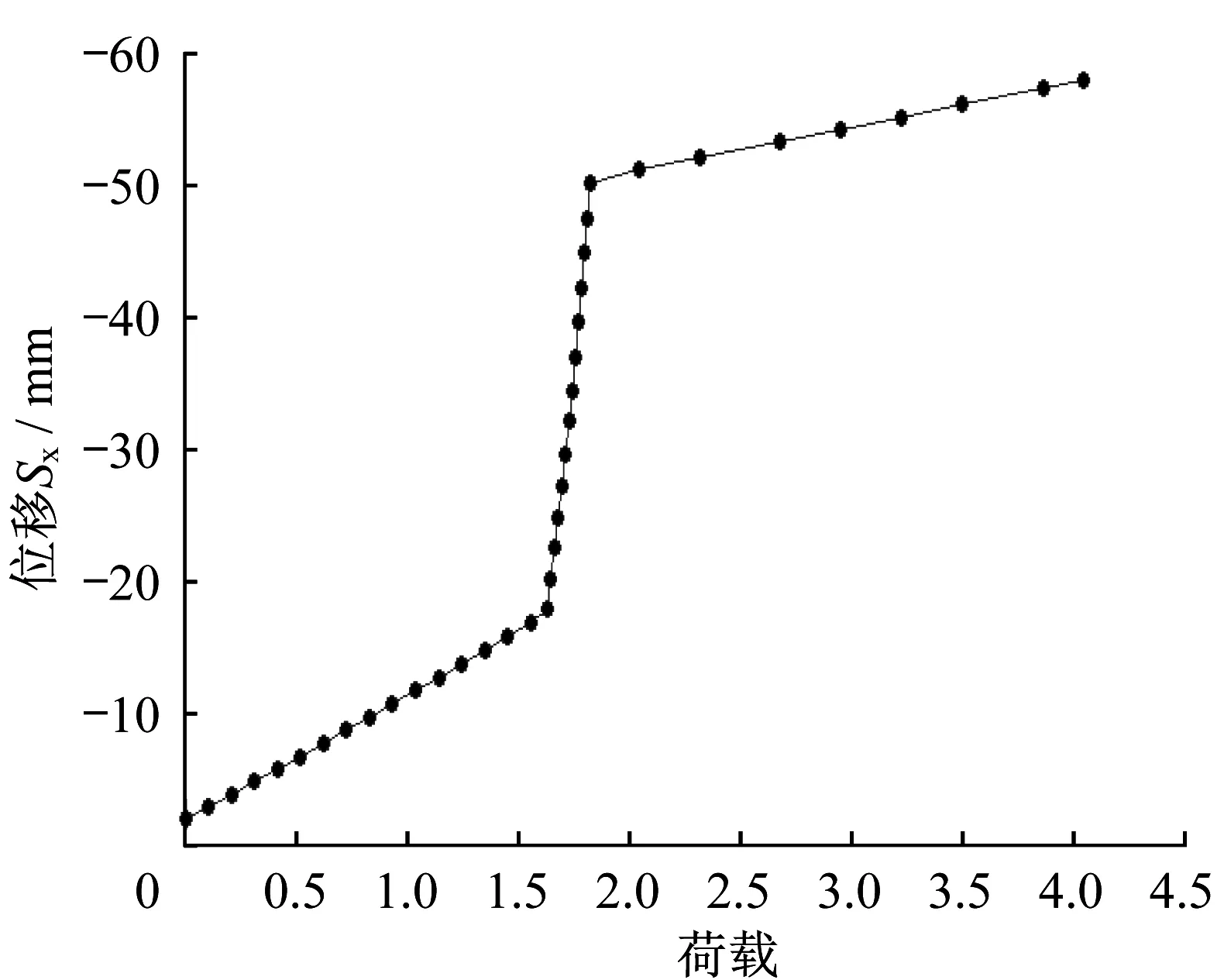
图12 风吸荷载作用下滑动端荷载—位移曲线Fig.12 Load-displacement curve for sliding end under wind suction load

在B-C 阶段，滑动端的位移达到其限值，使得上弦杆的轴向位移受限制，因而上弦杆的轴拉力迅速增大，此时上弦杆靠轴拉力的水平分力来抵抗增加的风荷载，此过程弯矩变化不大。从B点开始，支座的水平变形受限，支座出现水平拉力，此时对应1.8倍风荷载标准值。此外支座设计水平力限值为200 kN，由图13可知，对应2.3倍风吸荷载标准值，因此可认为，该结构最大能承受2.3倍风吸荷载标准值，此时张弦梁跨中的竖向位移为0.306 m（1/100）。

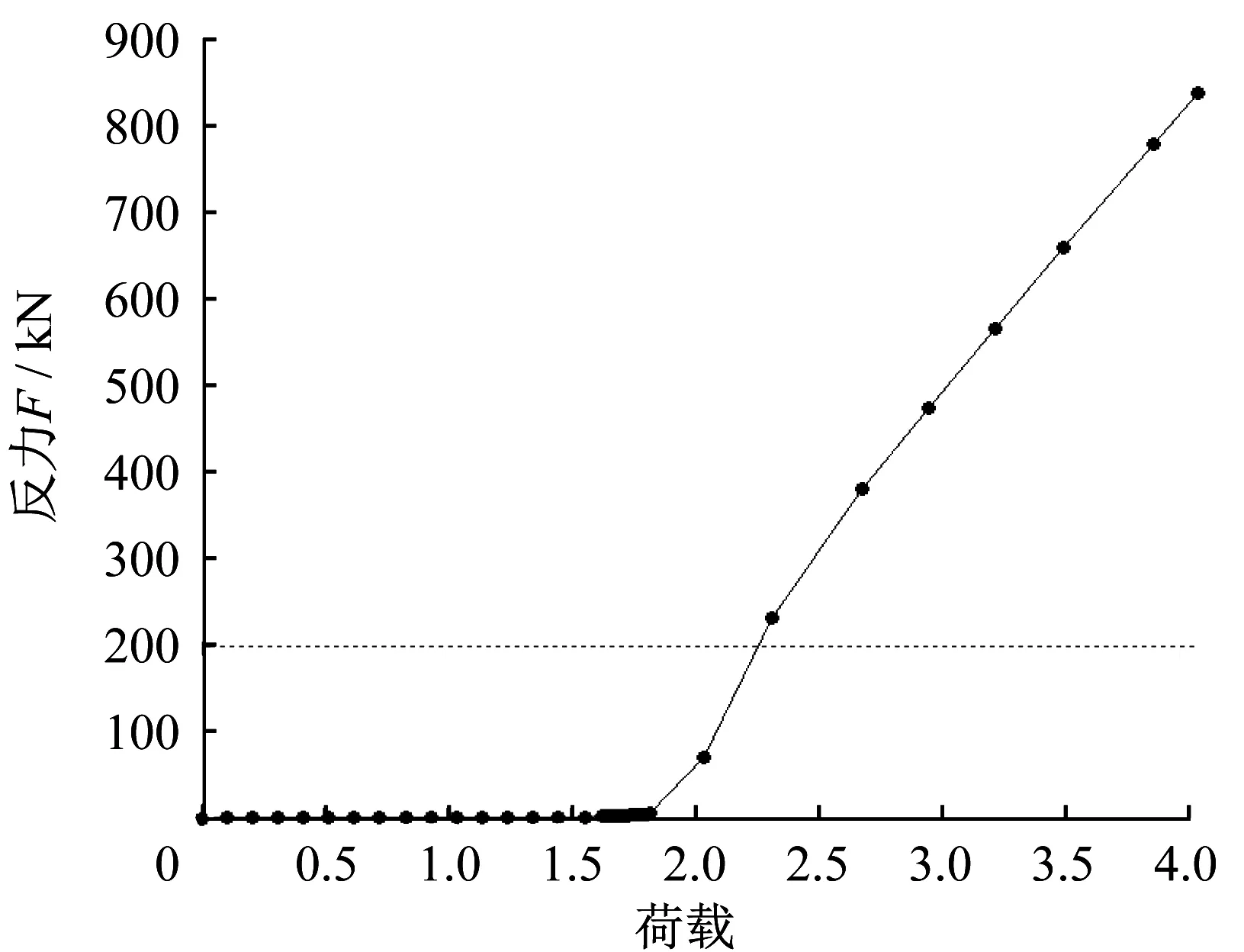
图13 风吸荷载作用下荷载-支座反力曲线Fig.13 Load-support reaction curve under wind suction load

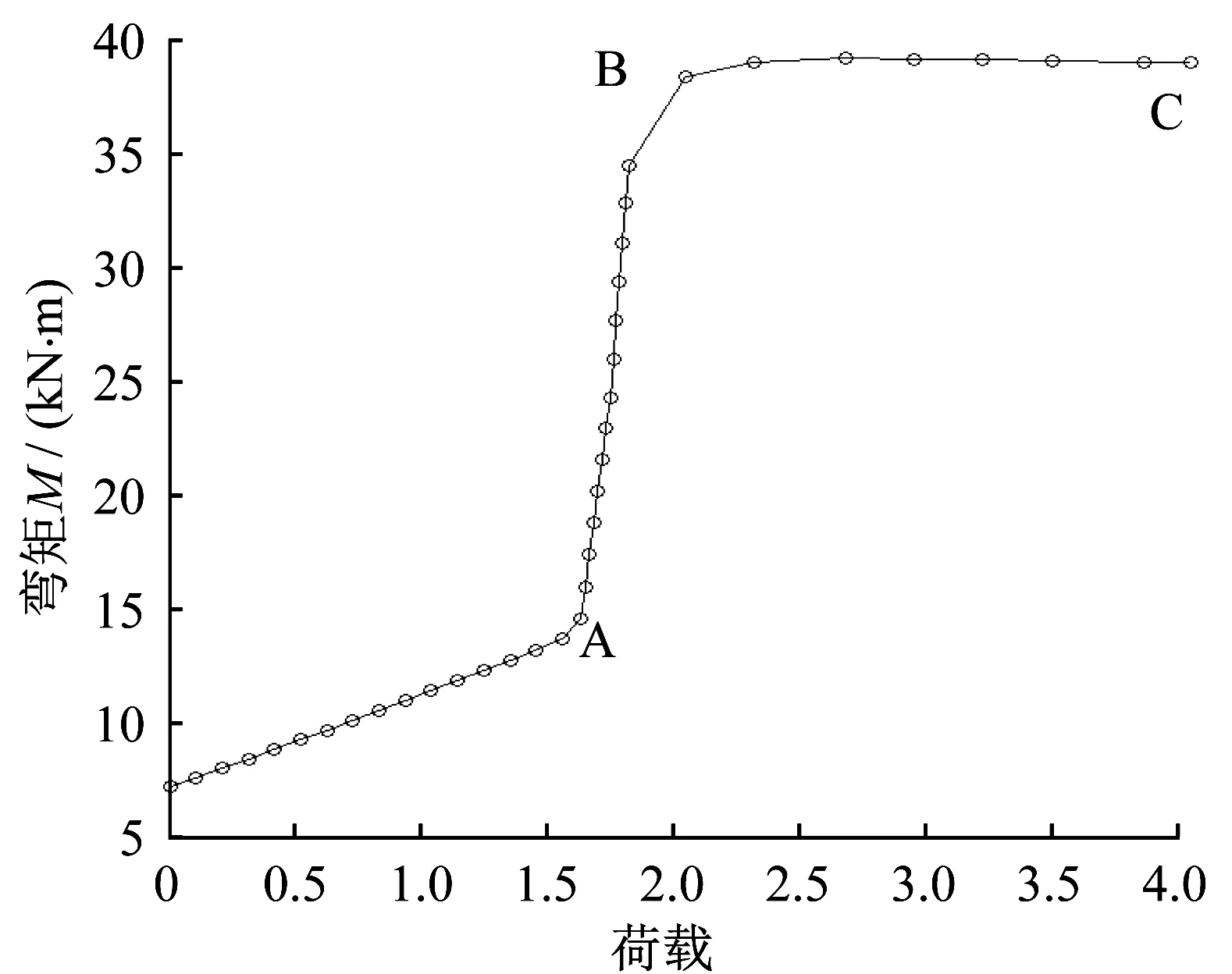
图14 风吸荷载作用下上弦杆荷载-弯矩曲线Fig.14 Load-bending moment curve for top chord under wind suction load

张弦梁结构在1.3 倍恒载+n 活荷载作用下，各弦杆的轴力—荷载曲线如图15 所示，张弦梁滑动端的荷载—位移曲线如图16所示。

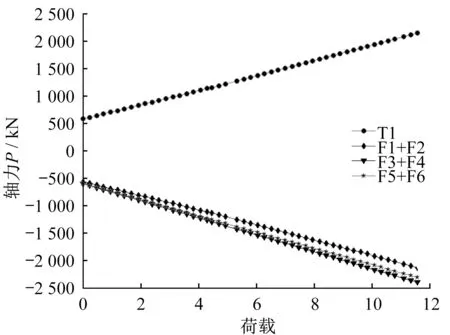
图15 活荷载作用下荷载-轴力曲线Fig.15 Load-axial force curve under live load

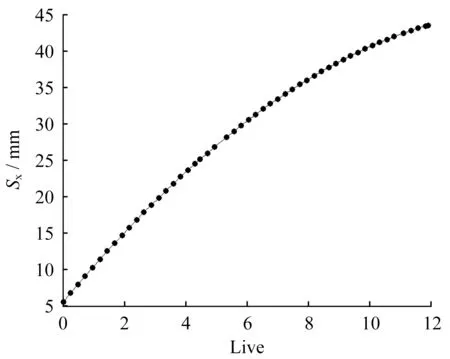
图16 活荷载作用下滑动端荷载-位移曲线Fig.16 Load-displacement curve for sliding end under live load

根据图15 可知随着活荷载增大上弦杆合力逐渐增大，下弦杆拉力逐渐增大，三者接近线性关系。根据图16，滑动端支座的水平位移随着活荷载增加而增大，二者为非线性关系。作用12 倍活载标准值时张弦梁跨中竖向位移为22 mm（1/1490），滑动端水平位移为45 mm，亦未达到支座位移限值50 mm，此时张弦梁上弦杆未进入塑性，张弦梁之间的水平系杆部分进入塑性，塑性铰分布如图17所示。

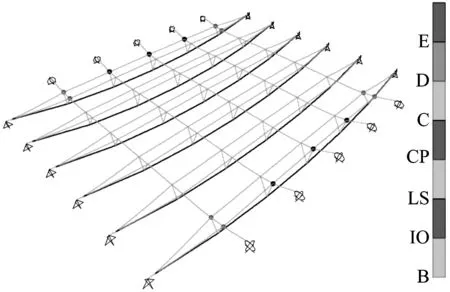
图17 1.3恒+12活荷载作用下塑性铰分布图Fig.17 Distribution of plastic hinges under 1.3 dead load+12 live load combination

3.3 节点分析

上弦杆与下弦杆相交处，由于受力复杂，需要进行节点分析，采用有限元软件建立分析模型。模型采用4 结点壳单元，材料选用理想弹塑性模型，弹性模量取为2.06×105MPa，屈服强度取为335 MPa，一般部位单元划分网格的尺寸为0.02/m，构件的约束条件如图18 所示。两上弦杆远端约束，下弦杆销轴孔处施加1.3恒载+1.5活载工况下下弦杆的拉力，支座端位置施加向上的支座反力。

图18 节点有限元分析模型Fig.18 Finite element analysis model of joint

对节点进行屈曲分析得到其一阶弹性屈曲因子为16.7，屈曲模态如图19 所示，为平面内屈曲。

图19 节点一阶屈曲模态Fig.19 1st buckling mode of joint

对节点进行极限承载力分析，在设计荷载作用下，节点的Mises应力分布如图20所示。

根据图20 可知，在设计荷载作用下，节点区最大应力为150 MPa，节点区处于弹性状态，节点区应力最大处为下弦杆销轴孔位置。节点满足设计荷载作用下的承载能力要求。

4 结 论

本文通过理论推导，得到张弦梁结构的曲线形状及下弦杆的初张力大小，这种曲线形状可以使得张弦梁在初张拉后，恒载作用下的竖向位移接近零。

对张弦梁屋盖进行了屈曲分析及极限承载力分析表明：结构在恒载+满布1.6 倍风吸荷载标准值作用下，下弦杆压曲；结构在恒载+满布2.3 倍风吸荷载标准值作用下支座水平力达到设计限值；结构在1.3 恒载+12 活载作用下，张弦梁之间的水平系杆部分进入塑性。

节点分析表明，在设计荷载作用下，节点区最大应力为150 MPa，节点区处于弹性状态，节点区应力最大处为下弦杆销轴孔位置。