差值扩展算法嵌入容量的研究与改进
郭彦鹏,胡文龙
(上海理工大学 光电信息与计算机工程学院,上海 200093)
图像隐写分为不可逆隐写和可逆隐写(又称无损数据隐藏)。对一幅图像嵌入信息一定会造成原始图像的改变,不可逆隐写中这种改变在提取秘密信息后仍然存在。可逆隐写除了关心秘密信息的隐写和提取外,还要求提取信息后载密图像能够恢复到原始载体图像。可逆隐写在一些对图像质量高敏感的许多特殊应用背景下有良好的应用前景,例如在军事图像和医学图像诊断等[1]。
已有众多文献介绍可逆隐写算法[2-8]。Tian 首先利用Haar 小波变换提出了基于差值扩展的可逆隐写算法[3](Difference Expansion,DE),该算法有较高的嵌入容量和较好的输出图像质量。之后众多学者针对DE算法又提出了一些变形延伸算法[4-9],Tai 等[4]通过直方图修改和移位来改善容量和输出图像质量,Lee 等[5]提出基于预测差值提高嵌入容量的算法,Chang 和Kieu[6]提出通过减少奇数像素值增加偶数像素值在一个像素对里垂直和水平嵌入秘密比特,Liu 等[7]提出采用双线性插值优化位置图提高嵌入容量,文献[8]提出通过直方图平移减小位置图大小,文献[9 ~10]提出基于直方图移位和预测误差的嵌入算法。这些算法都没有讨论利用像素对差值的相关性提高位置图的压缩效率。
1 DE 隐写
1.1 DE 算法原理
文献[4]根据图像的冗余空间提出差值扩展可逆隐写算法,冗余空间为相邻像素对可扩展差值的集合。
本文以8 位灰度图像为例介绍冗余空间。任取一个相邻像素对(x,y),x,y∈Z,0≤x,y≤255。定义像素对的平均值l 和差值h 为


式(1)和式(2)建立了相邻像素对(x,y)和(l,h)一一对应的变换关系。
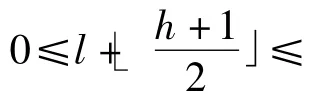
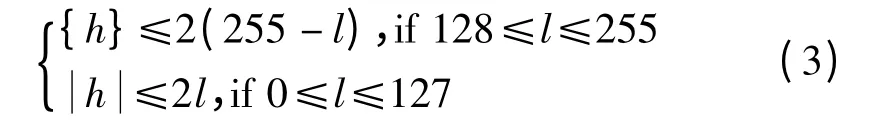
根据差值h 满足的条件,可将差值h 分为可扩展差值、可变换差值和不可变换差值。可扩展差值是可利用的冗余空间。
可扩展差值:将差值乘以2(左移1 位),末位嵌入一个秘密信息比特,嵌入后的差值hb=2×h+b,b 为0或1。嵌入后的像素对的灰度值一个变大一个变小,幅度约为为满足嵌入后像素灰度值不溢出,根据式(3)可扩展差值h 应满足(255-l),2l+1)。
放风时,定植后棚外温度还不是太稳定,相对较低,所以要放腰风,不能放底风。进入6月份以后,外界温度逐渐升高,可以加大放风量。进入7~8月份高温季节,可以把风一放到底,同时可以昼夜放风。下雨时要及时关风,防止雨水进入棚内。温度计要挂在棚的中央,高度在作物生长点以上10厘米。随着作物生长温度计不断提升,最后定位在1.2米左右。
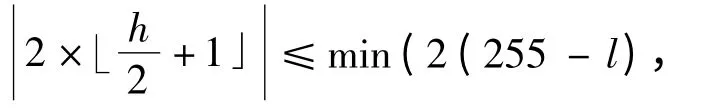
可扩展差值属于可变换差值,且经过差值扩展后仍属于可变换差值。可变换差值经过LSB 替换后还未可变换差值,不可变换差值在DE 算法嵌入前后不变。
1.2 DE 算法关键技术
位置图是DE 算法及其变形延伸算法的关键技术。对载体图像嵌入秘密信息时,对可扩展差值中满足阈值条件的差值,采用扩展差值算法添加1 bit。对可变换差值采用LSB 替换的方法嵌入1 bit。译码器从载密图像提取秘密信息和恢复原始图像时,需要知道载秘图像中像素对差值采用哪种嵌入方法,还需了解从哪开始解密。因此,需要产生一个位置图。
位置图是一个比特流,每个比特值标识一个像素对差值在嵌入时是作为可扩展差值(比特值为1)还是可变换差值(比特值为0),位置图的比特个数等于载体图像像素对个数,每个像素对最多只能嵌入1 bit,所以对位置图的压缩效率直接决定了嵌入容量的大小和输出载密图像的质量。
由前面讨论可知,经DE 算法隐写前后,载体图像和载密图像的像素对差值有表1 所示的变化。

表1 差值隐写前后属性
可扩展差值经扩展嵌入后是可变换差值,可变换差值经过替换LSB 嵌入后仍是可变换差值。所以,译码器可首先提取载密图像中所有的可变换差值得到一维数组,提取差值数组的LSB 得到一维比特流,对一维比特流根据位置图和原始LSB 流解析提取出秘密信息并恢复载密图像到原始状态。
2 算法改进和分析
2.1 扫描顺序对位置图的影响
首先定义一个衡量不同阈值下用于恢复载体图像的压缩位置图大小的定义

其中,Ne是压缩位置图比特数;pix 是载体图像差值的总数;k 为阈值大小。
压缩位置图的大小受不同扫描配对方法的影响较大。表2 是对灰度图像Lena、Barbara、Baboon、Peppers和Goldhill 采用DE 算法,在阈值50 下分别采用水平(Horizon,H)、垂直(Vertical,V)和Zigzag 扫描配对顺序求得的压缩位置图的大小,实验使用游程编码(Run-Length Coding,RLC)压缩位置图。
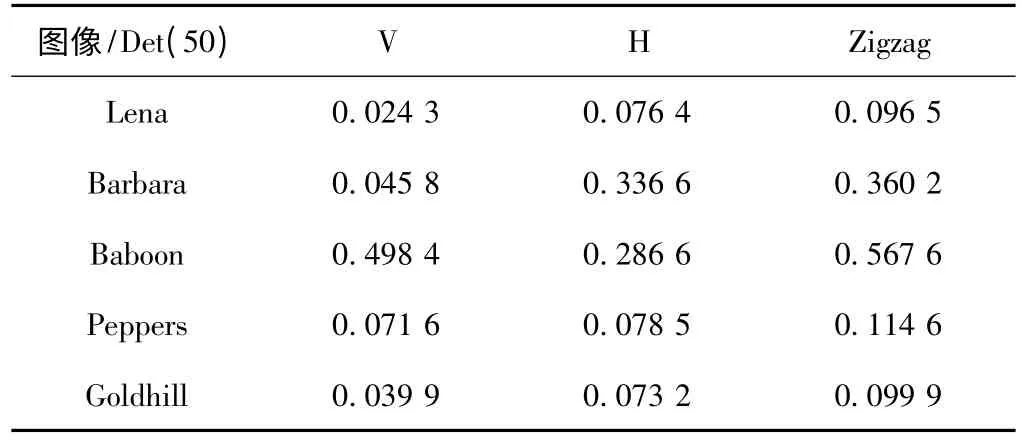
表2 DE 算法压缩位置图大小
由表2 可得出,在相同阈值下同一副图像采用不同的配对顺序对压缩位置图大小影响较大,由于Zigzag扫描路径比水平和垂直扫描路径更长,通常情况下Zigzag 压缩位置图效果较差。为获取更有效的压缩位置图,得到更大的隐写容量和提高嵌入后图像的质量,需根据图像像素的局部相关性选择最优的配对顺序。
2.2 差值矩阵的相关性分析
载体图像像素的局部相关性对选择扫描顺序的影响,启发本文对像素对差值相关性影响的研究。DE 算法对Lena 使用垂直或水平扫描顺序求像素对差值得到一维差值数组,再对该一维差值数组按照阈值生成位置图后压缩为比特流,这种算法忽略了利用差值的相关性提高位置图的压缩效率。如图1 所示,任取Lena图像一个的像素块,按垂直扫描求差值,明显对差值矩阵按水平扫描得到差值数组的相关性比按垂直扫描更好。
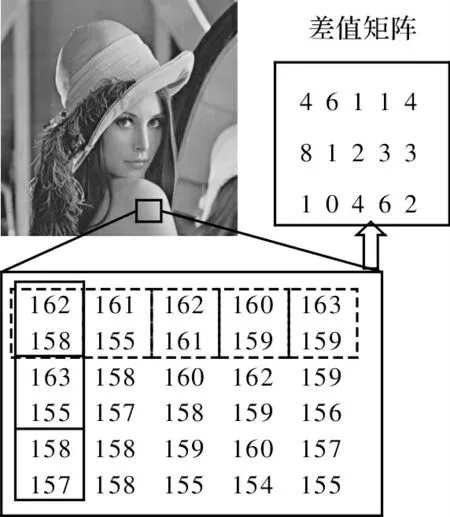
图1 Lena 像素对差值
对上节使用的5 幅图像,使用垂直扫描求差值后将得到的一维差值数组变换为与载体图像对应的256×512 差值矩阵,然后水平扫描差值矩阵为一维数组,根据阈值生成位置图后使用RLC 压缩位置图,求垂直扫描转水平扫描方法(Vertical to Horizon,VtoH)压缩位置图的大小。同理求水平扫描转垂直扫描方法(Horizon to Vertical,HtoV)压缩位置图大小。由于已讨论过Zigzag 扫描像素的相关性较差,后续不再针对Zigzag 扫描讨论差值数组的相关性。实验结果如表3所示。

表3 利用相关性求压缩位置图大小
对比表2 和表3 所示,Lena、Baboon、Peppers 和Goldhill 利用差值矩阵的相关性显著提高了位置图的压缩率,Goldhill 压缩效果最明显,HtoV 扫描的压缩位置图大小较原算法的H 扫描压缩了46%,可利用差值的相关性进一步压缩位置图。
2.3 算法改进
根据以上讨论,提出针对DE 算法利用差值相关性提高压缩位置图压缩率的改进算法如下:
嵌入信息。首先按最优顺序对载体图像每两个相邻像素配成一对,按式(1)求差值得到一维数组{h1,h2,…,hn}。不同载体图像的最优顺序不同,需要从水平、垂直路径扫描顺序中选择。将差值数组转换为与载体像素对位置对应的矩阵,转置差值矩阵后按照最优顺序扫描为一维数组,按照文献[4]方法生成压缩位置图比特流和嵌入秘密信息获得载密图像。
提取信息。首先按最优顺序扫描载体图像所有可变换像素对差值得到一维比特流。根据头文件分别提取出压缩位置图比特流、原始LSB 比特流和秘密信息波特率。解压压缩位置图为一维比特流,根据位置图比特流的标识信息恢复载密图像到原始载体图像。
3 实验结果
实验首先对比改进算法与DE 算法在不同阈值下压缩位置图的比特数,载体图像采用上节使用的5 幅512×512 灰度图片。改进算法和DE 算法均采用Matlab 实现,采用RLC 压缩位置图。
Lena 嵌入容量大小随阈值的变化关系如图2 所示。图2(a)是DE 算法水平扫描配对和改进算法的比较,在阈值20 ~35 之间改进算法的压缩位置图大小比DE 算法减小近20%,约25 000 bit;图2(b)为DE 算法垂直扫描和改进算法的比较,在阈值10 ~22 之间改进算法的压缩位置图大小同样比DE 算法约减小15%,多提供近20 000 个比特的嵌入空间。图2(a)和图2(b)均显示在阈值>80 后改进算法失去作用,这是因为随着阈值增大,差值数组中可变换差值迅速增多,最终只剩下不可变换差值影响压缩位置图的大小。
表4 是对Lena 采用两种算法嵌入秘密信息时PSNR 随嵌入率变化的数据,秘密信息采用Matlab 的rand()函数生成的0、1 均匀分布数组。表4 数据表明,由于改进算法提高了对位置图的压缩效率获得了更大的嵌入空间,输出图像质量在嵌入率0.1 ~0.35之间改进算法比DE 算法平均提高了1 PSNR,最高提高了1.5 PSNR。
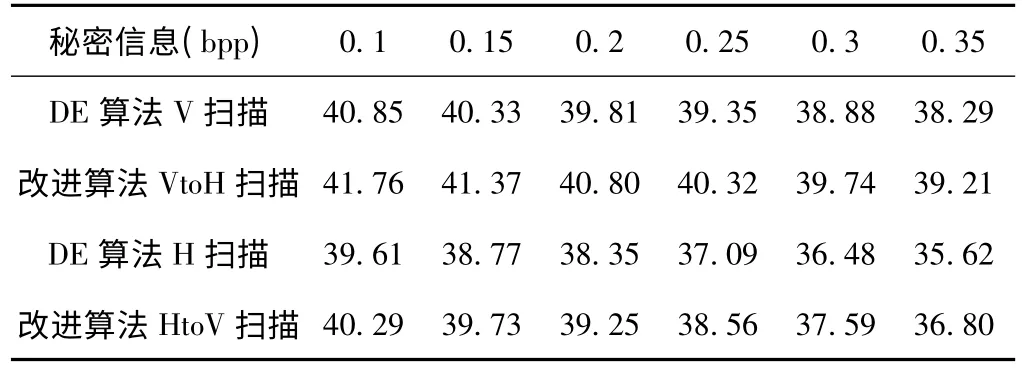
表4 Lena 改进算法与DE 算法PSNR
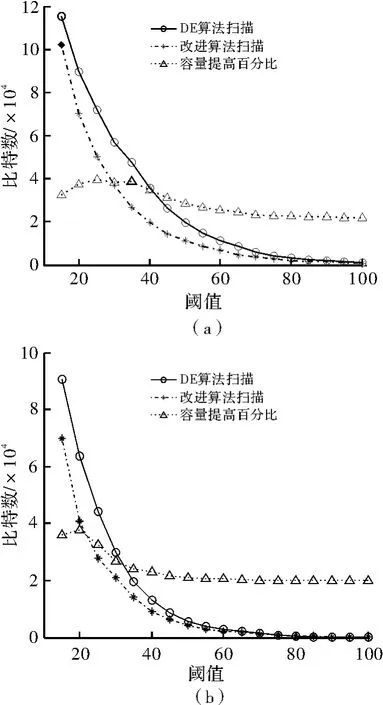
图2 Lena 嵌入容量随阈值的变化
4 结束语
本文对差值扩展算法的关键技术压缩位图压的缩效率进行研究,提出利用差值矩阵转置后扫描生成的位置图相关性比原算法更好来提高位置图的压缩效率,进而提高嵌入容量和输出图像质量。实验结果表明该算法在阈值较小时可显著提高嵌入容量,输出图像在0.1 ~0.3 bpp 嵌入率下平均提高了1 PSNR。
[1] Fridrich J,Goljan M,Du R.Lossless data embedding-new paradigm in digital watermarking[J].EURASIP Journal on Advances in Signal Processing,2002,2002(2):185-196.
[2] Celik M U,Sharma G,Tekalp A M.Lossless generalized-LSB data embedding[J].IEEE Transactions on Image Processing,2005,14(2):253-266.
[3] Tian Jun.Reversible data embedding using a difference expansion[J].IEEE Transactions on Circuits and Systems for Video Technology,2003,13(8):890-896.
[4] Tai W L,Yeh C M,Chang C C.Reversible data hiding based on histogram modification of pixel differences[J].IEEE Transactions on Circuits and Systems for Video Technology,2009,19(6):904-908.
[5] Lee Chinfeng,Chen Hsingling,Tso Haokuan.Embedding capacity raising in reversible data hiding based on prediction of difference expansion[J].Journal of Systems and Software,2010,83(10):1864-1872.
[6] Chang Chinchen,Duc Kieu.A reversible data hiding scheme using complementary embedding strategy[J].Information Sciences,2010,180(16):3045-3058.
[7] Liu Y C,Wu H C,Yu S S.Adaptive DE-based reversible steganographic technique using bilinear interpolation and simplified location map[J].Multimedia Tools and Applications,2011(52):263-276.
[8] 陈康康,王建军.一种基于差值扩展大容量可逆信息隐藏新算法[J].信息与电子工程,2010,8(1):58-62.
[9] 李建伟,胡永健,陈开英.利用预测误差直方图平移的可逆数据隐藏技术[J].中国图象图形学报,2008,14(6):1088-1095.
[10]Lee C F,Chen H L.Reversible data hiding based on histogram modification of prediction-error[J].Imaging Science Journal,2011(59):278-292.

