钢桥面板顶板-纵肋双面焊的焊接残余应力分析与统一分布模型
王 喆 丁幼亮,* 钟 雯 耿方方
(1.东南大学混凝土及预应力混凝土结构教育部重点实验室,南京210096;2.南京工程学院建筑工程学院,南京211167)
0 引 言
单面焊焊接的正交异性钢桥存在一定的初始缺陷,在车辆荷载的往复作用下容易发生疲劳开裂,而双面焊焊接可以在一定程度上改善焊接节点的疲劳性能。目前,板件厚度的增加对单面焊钢桥疲劳稳定性能的影响已较为明朗,但是钢桥面板的双面焊焊接残余应力分布及其随板件厚度的变化尚不明确。
国内外学者对于单面焊下焊接残余应力的计算模拟结果已进行了大量的研究,且对双面焊的焊接模拟有了初步的研究。卫星等[1]采用了有限元可以有效模拟焊接节点的温度场、应力场;赵秋等[2]研究了钢桥面板顶板纵肋纵向焊接残余应力在某一板件厚度下的分布;邵珂夫[3]给出了在不同接头形式下,焊接残余应力在钢桥焊接节点的分布情况;瞿伟杰等[4]对钢桥整体节点焊接过程中的温度场和应力场进行了模拟分析;曹宝雅等[5]研究了不同板件厚度下钢桥面板单面焊焊接残余应力分布情况,并给出了单面焊焊接残余应力统一分布模型;Cui Chuang 等[6]做了顶板纵肋双面焊焊接残余应力试验,并给出了相应点的焊接残余应力试验值。以上研究大多针对单面焊的焊接残余应力分布情况,或仅粗略分析了某一特定板件厚度下的双面焊焊接残余应力试验值,关于板件厚度变化对钢桥面板双面焊焊接残余应力分布影响仍缺乏规律的讨论。
基于以上情况,本文建立了钢桥面板双面焊顶板纵肋模型并改变其板件厚度,给出了双面焊纵向及横向焊接残余应力分布图,研究了不同板件厚度对双面焊焊接残余应力的影响,并建立了双面焊焊接残余应力统一分布模型。
1 双面焊焊接残余应力数值模拟
1.1 双面焊有限元模型
1.1.1 模型参数
根据目前工程中正交异性钢桥面板常用板件厚度,此节中建立的有限元模型顶板初始厚度为16 mm,肋板初始厚度为6mm,在U 肋上开坡口,采用双面焊焊接形式。焊件截面及焊缝尺寸如图1所示。
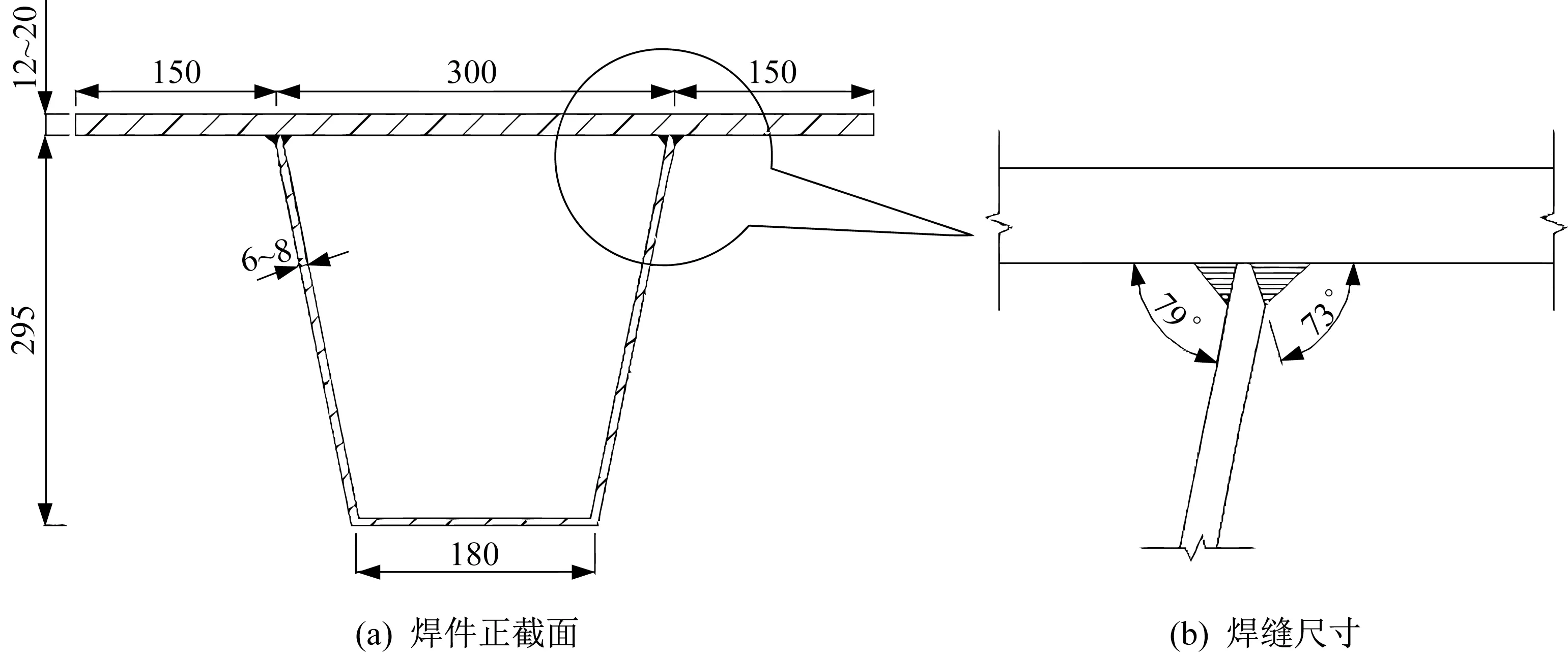
图1 焊件截面及焊缝尺寸图(单位:mm)Fig.1 Weldment section and weld size(Unit:mm)
图2为模型网格划分及边界条件,并提供了模型的坐标系方向:坐标原点位于顶板一侧横截面底边中心上方1 mm 处,X 方向为垂直于焊缝方向(横向),Y 方向为纵肋高度方向(竖向),Z 方向为沿焊缝方向(纵向)。由于焊件具有对称性,模型仅取半结构进行建立,因此模型的位移边界条件如图2(b)所示:对称约束施加于顶板-纵肋对称截面处,Y 方向约束施加于顶板左右两侧,Z 方向约束施加于顶板横截面一侧。
模型采用Solid70 单元,因焊缝附近应力改变较为明显,网格最小尺寸设为2 mm;焊缝远离区网格最大尺寸设为8 mm,仅进行粗略划分。
1.1.2 材料热物理与力学参数
在建立有限元模型时,将顶板、纵肋材料设置为Q345 钢,焊条选用E50 型,其热物理与力学参数均引用文献[5]中的数值。
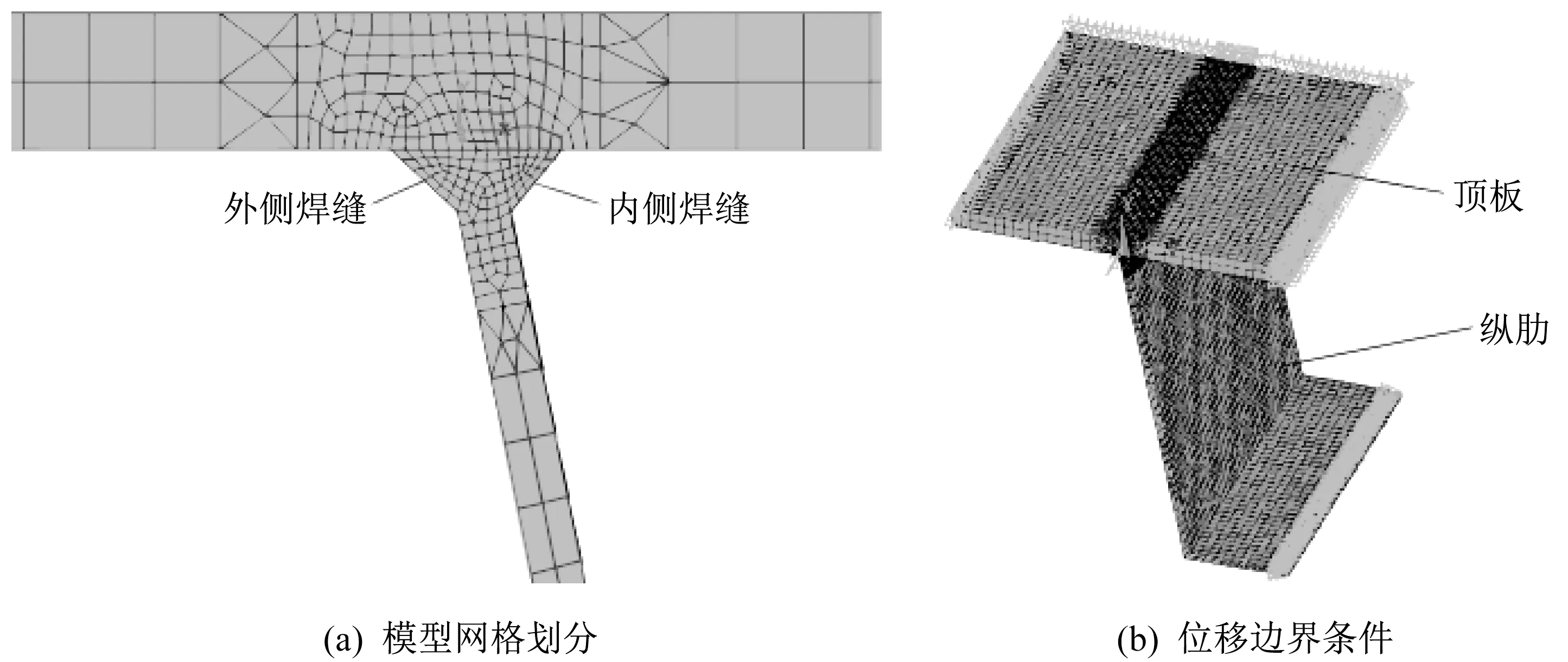
图2 模型网格划分及边界条件Fig.2 Model meshing and boundary conditions
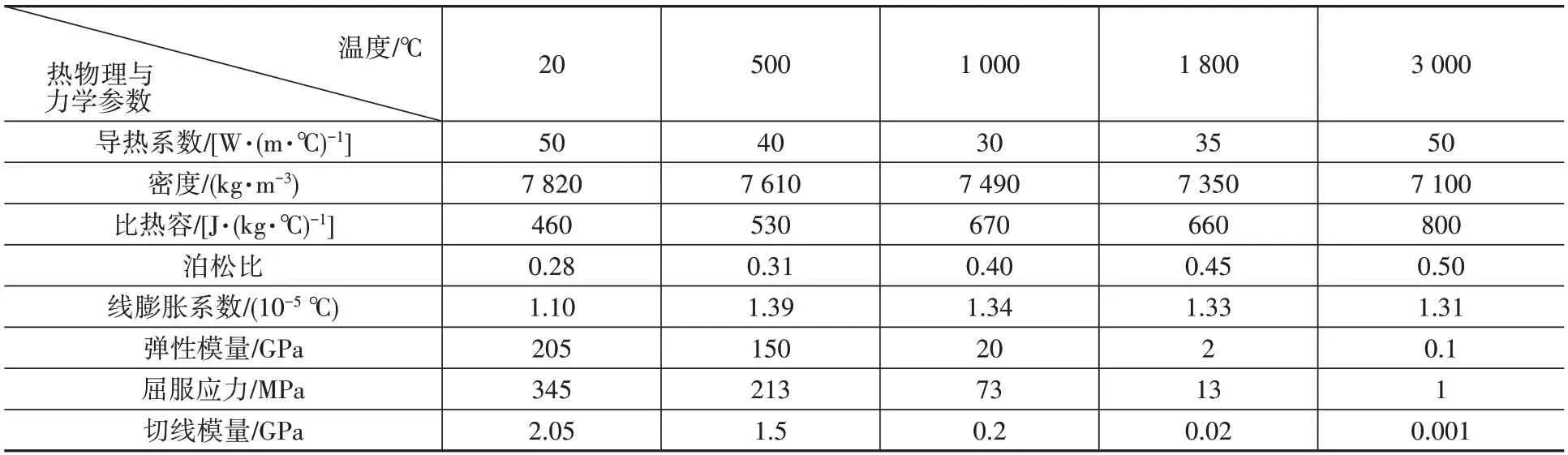
表1 不同温度下Q345钢的热物理与力学参数Table 1 Thermophysical and mechanical parameters of Q345 steel at different temperatures
1.1.3 材料本构关系
在数值模拟中,将材料定义为理想弹塑性材料,其本构关系如图3所示。
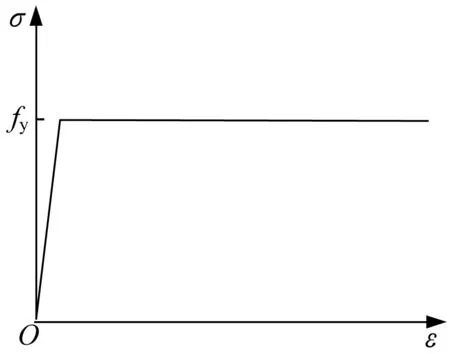
图3 理想弹塑性材料本构关系Fig.3 Constitutive relation of ideal elastoplastic material
1.1.4 温度场与应力场模拟
顶板纵肋焊接属于典型的非线性问题,故在温度场和应力场模拟中采用Solid185 单元。结构分析的应力场大致由焊接温度场决定,因此数值模拟先通过生热率和生死单元的方法模拟焊接过程。本文模型为双面焊,外侧焊缝焊接时间为30 s,冷却300 s后进行内侧焊缝焊接,然后逐渐冷却至室温。温度场计算完成后得到热分析结果,将其以体荷载的形式施加在节点上,进行结构总体分析,即采用热-应力耦合法。
1.2 双面焊焊接残余应力分析
1.2.1 纵向分布
沿纵向分布的顶板-纵肋双面焊焊接残余应力分布图如图4 所示。图中,路径1-6 分别为外侧焊缝靠顶板焊趾、外侧焊缝焊根、外侧焊缝靠肋板焊趾、内侧焊缝焊根、内侧焊缝靠顶板焊趾、内侧焊缝靠肋板焊趾处沿Z方向的应力分布;z为节点的Z方向坐标值。由图可知:①纵向和横向残余应力分布曲线在中间一长段数值较大且基本呈水平发展,在离焊缝两端约0.03 m 处迅速下降,两者变化规律相同,可知双面焊焊接残余应力不随焊缝实际长度变化。在实际工程中,一段纵肋长度远大于有限元模型中的焊缝长度,因此在考察沿横向分布的双面焊焊接残余应力时,取沿焊缝方向靠中间段截面的残余应力进行研究(本文所取横截面Z方向坐标值为0.15 m)。②横向残余应力在外侧焊缝靠顶板焊趾处达到最大值220 MPa;纵向残余应力在内侧焊缝焊根处达到最大值400 MPa,纵向残余应力最大值约为横向残余应力的1.8倍。
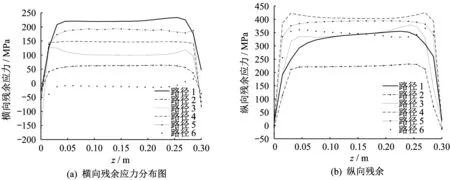
图4 沿纵向双面焊焊接残余应力分布Fig.4 Residual stress distribution along the longitudinal direction of double-sided welding
1.2.2 横向分布
图5 为沿横向分布的焊接残余应力在焊缝侧顶板表面、焊缝外侧顶板表面和顶板中线处分布图。图中,横坐标z 值为相应节点相对于顶板外侧边界的X方向坐标差值。
由图5(a)可知:①横向残余应力在顶板三条路径均呈现为离焊缝越近,应力值越大。②在靠近焊缝区,顶板中线处的焊接残余应力为压应力,顶板上下表面的焊接残余应力为拉应力。③横向残余应力在焊缝侧顶板表面的外侧焊缝焊趾处达到最大值250 MPa,曲线另有两个峰值位于焊缝侧顶板表面的内侧焊缝中心和焊趾处,约为最大值的80%。
由图5(b)可知:①纵向残余应力在顶板三条路径处均呈现为离焊缝越近,应力值越大。②在靠近焊缝区,同横向残余应力一致,顶板上下表面的焊接残余应力为拉应力,顶板中线处的焊接残余应力为压应力。③纵向残余应力在焊缝侧顶板表面的内侧焊缝焊根处达到最大值,约为445 MPa,曲线另有2 个峰值位于外侧焊缝中心和焊根处,三个峰值点应力值均已超过材料的屈服强度。

图5 沿横向双面焊焊接残余应力分布Fig.5 Residual stress distribution along the transverse direction of double-sided welding
1.2.3 试验验证
图6 为文献[6]中钢桥面板顶板纵肋双面焊焊接残余应力的试验结果与上文数值模拟结果的对比图。为使对比结果更为可靠,数值模拟模型与试验采用相同的板件厚度,均为顶板厚16 mm,纵肋厚8 mm。故图中数值模拟曲线采用的是后文有限元模拟中得到的焊缝侧顶板表面的横向残余应力,试验值采用的是文献[4]中沿path2 的横向残余应力。
由图6可知:①数值模拟与试验中的横向残余应力沿顶板均为拉应力,且具有相同变化规律,即横向残余应力离焊缝越远数值越小,在靠近焊缝处突然增大。②由于试验模型的边界条件没有准确交代,试验结果在模型外边界稍大于数值模拟结果,但在焊缝处和模型对称边处数值模拟结果与试验结果相吻合,说明本文数值模拟结果可靠。

图6 横向残余应力理论计算值与实测值的比较Fig.6 Comparison of theoretical calculated values and measured values of transverse residual stress
2 板件厚度变化对双面焊焊接残余应力的影响
通过1.2节分析可知,横向分布的焊接残余应力值和纵向分布的焊接残余应力值均在焊缝侧顶板表面达到最大,分析时最不利,因此取焊缝侧顶板表面的残余应力作为本节的分析对象。为方便表达,本文引用文献[3]中对板件厚度的描述方法,将顶板和肋板分别简记为D和L。
2.1 顶板厚度变化的影响
当考察顶板厚度变化对双面焊焊接残余应力的影响时,将肋板厚度设置为6 mm,沿横向分布的焊接残余应力曲线如图7 所示。由图7(a)可知:①横向残余应力在焊缝侧表面均表现为拉应力,且在不同顶板厚度下变化规律相同,曲线有3个峰值点,分别位于外侧焊缝焊趾处、内侧焊缝中心处和内侧焊缝焊趾处,峰值应力为290 MPa,约为材料屈服应力的85%。②不同顶板厚度下的横向残余应力最大值相差较大,顶板厚度12 mm 时横向残余应力最大值为210 MPa,顶板厚度20 mm时横向残余应力最大值为290 MPa,后者比前者大40%左右。③两道焊缝中间的横向残余应力较小,均在25~50 MPa,远小于焊缝处的应力。④在焊缝区,应力值随板件厚度的增加而增大;在远离焊缝区,应力值大致随板件厚度的增加而减小。
由图7(b)可知:①纵向残余应力在不同顶板厚度下变化规律相同,曲线包含3 个峰值点,分别位于外侧焊缝中心处、外侧焊缝焊根处和内侧焊缝焊根处,在内侧焊缝焊根处达到最大值,约为445 MPa,三处峰值应力均已超过材料的屈服强度。②不同顶板厚度的纵向残余应力最大值相差不大,顶板厚度12 mm 的纵向残余应力最大值为445 MPa,顶板厚度20 mm的纵向残余应力最大值为450 MPa,相差5 MPa。③纵向残余应力在焊缝区随顶板厚度的增加而增大。在远离焊缝区表现为压应力,随板件厚度的增加而减小。

图7 随顶板厚度变化的焊接残余应力分布曲线Fig.7 Welding residual stress distribution curve with thickness variation of top plate
2.2 纵肋厚度变化的影响
当考察肋板厚度变化对双面焊焊接残余应力的影响时,将顶板厚度设置为16mm,沿横向分布的焊接残余应力曲线如图8所示。
由图8(a)可知:①横向残余应力在不同肋板厚度下变化规律相同。②肋板厚度6 mm 时横向应力最大值为255 MPa,肋板厚度8 mm 时横向应力最大值246 MPa,峰值应力仅相差9 MPa。③在外侧焊缝处,横向残余应力值随肋板厚度的增加而减小;在内侧焊缝和远离焊缝处,横向残余应力值随肋板厚度的增加而增大。
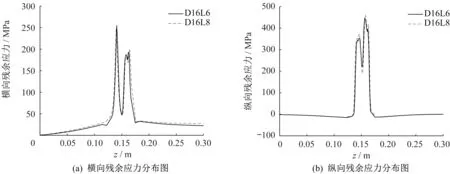
图8 随肋板厚度变化的焊接残余应力分布曲线Fig.8 Welding residual stress distribution curve with thickness variation of rib
由图8(b)可知:①纵向残余应力在不同肋板厚度下变化规律相同。②肋板厚度6 mm 的纵向应力最大值为445 MPa,肋板厚度8 mm 的纵向应力最大值462 MPa,峰值应力相差17 MPa。③沿靠焊缝侧顶板表面,应力值随肋板厚度的增加而增大。
3 焊接残余应力统一分布模型
双面焊下焊接残余应力最大值随顶板厚度变化的拟合曲线见图9,图中肋板厚度取为6 mm。拟合方程如下:
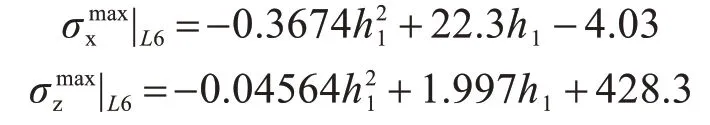
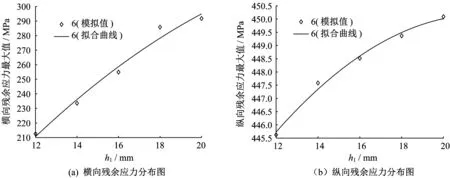
图9 焊接残余应力随顶板厚度变化时最大值拟合曲线Fig.9 Fitting curve of maximum welding residual stress with thickness variation of top plate
由图9(a)可知:①肋板厚度固定时,顶板厚度的增加会使双面焊横向残余应力值增大;顶板厚度12 mm 时横向残余应力最大值为210 MPa,顶板厚度20 mm时横向残余应力最大值为290 MPa,后者比前者大40%左右。②顶板厚度增加时焊缝附近的横向残余应力会显著增大,但增加顶板厚度有助于降低车辆荷载下构件的应力,因此需要进一步研究疲劳性能随顶板厚度增加的变化规律。
由图9(b)可知:①肋板厚度固定时,顶板厚度的增加会使纵向残余应力增大,顶板厚度20 mm 时纵向残余应力最大值比顶板厚度12 mm时大5 MPa。②顶板厚度的增加对焊缝附近的纵向残余应力影响较小,且车辆荷载作用下的应力会随板件厚度的增加而减小,因此分析得知,在工程中可通过增加板件厚度来提高桥梁稳定承载力。
顶板纵肋横向、纵向双面焊焊接残余应力统一分布模型如图10 和图11 所示。图中,p 为两道焊缝间未熔透长度;B 为顶板宽度;bw1为顶板外侧焊缝宽度;bw2为顶板内侧焊缝宽度;σmaxx为横向残余应力在顶板处最大值;σxt1为横向残余应力在顶板两道焊缝中间处取值,取σxt1=0.2σmaxx;σxt2为横向残余应力在顶板远离焊缝区处取值,取σxt2=0.15σmaxx;σmaxz为纵向残余拉应力在顶板处最大值;σzt1为纵向残余拉应力在顶板两道焊缝中间处取值,取σzt1=0.5σmaxz;σzt2为纵向残余压应力在顶板远离焊缝区取值,取σzt1=16 MPa。除σzt2外其余应力均为拉应力。
由图10、图11 可知,双面焊焊接残余应力统一分布模型具有以下特点:①横向残余应力曲线包含3 个峰值点,分别位于外侧焊缝焊趾、内侧焊缝中心和内侧焊缝焊趾附近2~3 mm范围内,模型近似认为位于外侧焊缝焊趾处、内侧焊缝中心处和内侧焊缝焊趾处;其中内侧焊缝中心和焊趾处的两个峰值相差不大,均为外侧焊缝焊趾处的80%或略小于80%,所以模型近似认为外侧焊缝焊趾处为应力最大值,内侧焊缝中心和焊趾处为应力最大值的80%。②纵向残余应力曲线包含3个峰值点,分别位于外侧焊缝中心、外侧焊缝焊根和内侧焊缝焊根的附近2~3 mm范围内,模型近似认为位于外侧焊缝中心处、外侧焊缝焊根处和内侧焊缝焊根处;其中外侧焊缝中心和焊根处的两个峰值相差不大,均为内侧焊缝焊根处的85%左右,所以模型近似认为内侧焊缝焊根处为应力最大值,外侧焊缝中心和焊根处为应力最大值的85%。③双面焊焊接残余应力在远离焊缝区数值较小,仅给出了近似分布规律。④本文给出的统一分布模型适用于顶板厚度为12~20 mm、肋板厚度为6 mm、材料为Q345 钢的钢桥面板顶板-纵肋双面焊焊接残余应力计算。

图10 沿顶板双面焊横向焊接残余应力统一分布模型Fig.10 Uniform distribution model of transverse residual stress of double-sided welding along top plate

图11 沿顶板双面焊纵向焊接残余应力统一分布模型Fig.11 Uniform distribution model of longitudinal residual stress of double-sided welding along top plate
4 结 论
(1)横向残余应力在焊缝侧顶板表面的外侧焊缝焊趾处达到最大值250 MPa,约为材料屈服强度的3/4。横向残余应力另有两个峰值位于焊缝侧顶板表面的内侧焊缝中心和焊趾处,约为最大值的80%。因此,进行顶板纵肋双面焊焊接节点疲劳分析时,顶板表面外侧焊缝焊趾、内侧焊缝中心和焊趾处的疲劳分析应被重点关注。
(2)纵向残余应力在焊缝侧顶板表面的内侧焊缝焊根处达到最大值,约为445 MPa。纵向残余应力另有两个峰值位于焊缝侧顶板表面的外侧焊缝中心和焊根处,约为最大值的85%,三处应力值均已超过材料屈服点,构件稳定极限承载力可能会因此降低。
(3)肋板厚度固定时,顶板厚度的增加会显著增大双面焊横向残余应力值。顶板厚度为12 mm时横向残余应力最大值比顶板厚度为20 mm时小40%左右。顶板厚度固定时,肋板厚度的增加对横向残余应力值的影响不明显;肋板厚度为6 mm时横向残余应力最大值比肋板厚度为8 mm 时大4%。因此,双面焊焊接节点的横向残余应力随顶板厚度的增加显著增大,但现阶段工程中为降低车辆荷载下构件的应力,常常增加顶板厚度,因此需要进一步研究钢桥面板疲劳性能随顶板厚度增加的变化规律。
(4)肋板厚度固定时,纵向残余应力最大值随顶板厚度的增加仅增大约1%。顶板厚度固定时,纵向残余应力最大值随肋板厚度的增加仅增大约2%。可知纵向残余应力几乎不随顶板和纵肋厚度的改变而变化,且车辆荷载下构件的应力会随板件厚度的增加而降低,因此增加板件厚度有利于后续钢桥面板疲劳分析。
(5)本文给出的统一分布模型适用于顶板厚度为12~20 mm、肋板厚度为6 mm、材料为Q345钢的钢桥面板顶板-纵肋双面焊焊接残余应力计算,为双面焊下顶板-纵肋焊接残余应力的进一步研究提供参考。

