双向张弦梁结构振动模态特性分析
徐蒙越 张 莉
(上海大学土木工程系,上海200444)
0 引 言
张弦梁结构在近20 年内发展迅速,是一类由上弦受压弯刚性构件,下弦受拉的柔性钢索,中间连以受压撑杆形成的混合结构体系。该结构受力合理,结构效率高,因而受到了建筑师的青睐,在很多工程中得到了应用,例如上海浦东国际机场候机楼[1]、广州国际会展中心[2]、哈尔滨国际体育会展中心[3]等。这些结构多采用多榀结构尺寸相同的张弦梁平行布置成屋面结构。
平面张弦梁结构受力合理,在初始态与受荷态几乎没有水平支反力,是一种比较理想的结构体系。该结构目前应用较多,富秋实提出了优化后的分段平面张弦梁结构[4],性能更优。但平面张弦梁结构平面外刚度较差,为改善这一缺点,发展了双向和多向张弦梁结构[5-6]。
张志宏等[7]基于计算参考构形,对平面张弦梁的计算分析理论等问题进行了讨论。刘开国[8]针对双向张弦梁结构提出了一种基于连续化假定的简化算法。目前双向张弦梁结构的动力特性分析仍然缺乏较为精确的计算方法。而模态分析作为结构动力特性研究的基础,本文结合有限元算例对张弦梁结构的自振模态特性进行参数分析,研究了张弦梁结构的基本模态特性。
1 结构自振特性计算假定及步骤
1.1 计算假定
双向张弦梁结构的模态特性计算采用以下基本假定:
(1)上弦所有节点均为刚接,梁单元为两节点三维弹性梁;下弦所有节点均为铰接,索单元为两节点三维杆单元。
(2)结构边界为铰接边界,一端节点约束三个方向的位移,另一端则仅约束竖向位移。
(3)结构始终处于弹性状态。
(4)荷载作用简化为等效节点质量,具体采用质量单元法。
1.2 计算步骤
双向张弦梁结构的模态特性有限元分析步骤如下:
(1)设定结构零状态坐标,对双向张弦梁结构进行参数化建模,采用初应变法将预应力施加在下弦拉索上。
(2)打开大变形效应与非线性效应,进行非线性有限元分析,求解结构初始态。
(3)采用质量单元法编制宏文件将面荷载转化为等效节点质量,并施加在初始态的模型相应节点上。
(4)采用Block Lanczos 法对结构进行模态分析,输出结构自振频率及振型参与系数等结果。
2 张弦梁结构自振特性
2.1 工程算例
算例为矩形双向张弦梁结构,模型如图1 所示,平面为边长40 m的正方形,上下弦曲面均为抛物面,矢跨比与垂跨比分别为1/25与1/20。上弦梁为300×600×8×15 的 方 钢 管,弹 性 模 量E=2.1×1011N/m2;中间撑杆为φ120× 6 圆钢管,弹性模量E=2.1×1011N/m2;下弦拉索均为φ5×55 钢丝束,弹性模量E=1.9×1011N/m2。计算考虑自重作用,钢材密度为7 850 kg/m3。上弦梁与撑杆选用Q345 钢材;下弦索材料极限抗拉强度为1 770 N/mm2,设计安全系数为3,应力限值[σ]=590 N/mm2。图1 中边界x=0与y=0节点约束三个方向的位移,另一端仅约束竖向位移,用以模拟实际工程中一端固定铰支座另一端滑动铰支座[10]。采用初应变法施加在全体下弦索单元上,预拉力P取值为300 kN,初应变具体计算如下:

屋面恒荷载为0.5 kN/m2,活荷载为1.0 kN/m2,设计工况为1.2×全跨恒荷载+1.4×全跨活荷载。

图1 模型简图Fig.1 Model sketch
2.2 分析结果
表1 为频率与模态参与系数。表中小于10-4的量均认为约等于零,rx,ry,rz依次为x,y,z 方向振型贡献率,MFx,MFy,MFz依次为x,y,z方向累计质量分数,ri为第i阶振型贡献率。
表1 结果表明,双向张弦梁结构的自振特性有以下特点:
(1)双向张弦梁结构以曲面水平方向振动为主,观察算例模型的前20 阶振型,x 与y 方向模态质量参与比例达70 %以上,z 向模态质量参与比例仅11.13%。本文认为算例模型的自振特性表现是受边界条件影响的结果,即在双向张弦梁结构的一端仅约束竖向位移,导致水平方向的模态质量参与比率远高于z向的模态质量参与比率。
(2)如表1 所示,双向张弦梁结构基频较高,说明该结构具有较好的结构刚度。振型分布较为稀疏,在一定范围呈较小的台阶型分布,算例中第1 阶与第2 阶自振频率差值为0.092 9 Hz,第9 阶与10 阶自振频率差值为0.174 4 Hz,第15 阶与第16 阶自振频率差值为0.086 9 Hz,第18 阶与第19阶自振频率差值为0.075 Hz。同时算例的基本周期为0.044 s,也表明该结构具有良好的结构刚度。
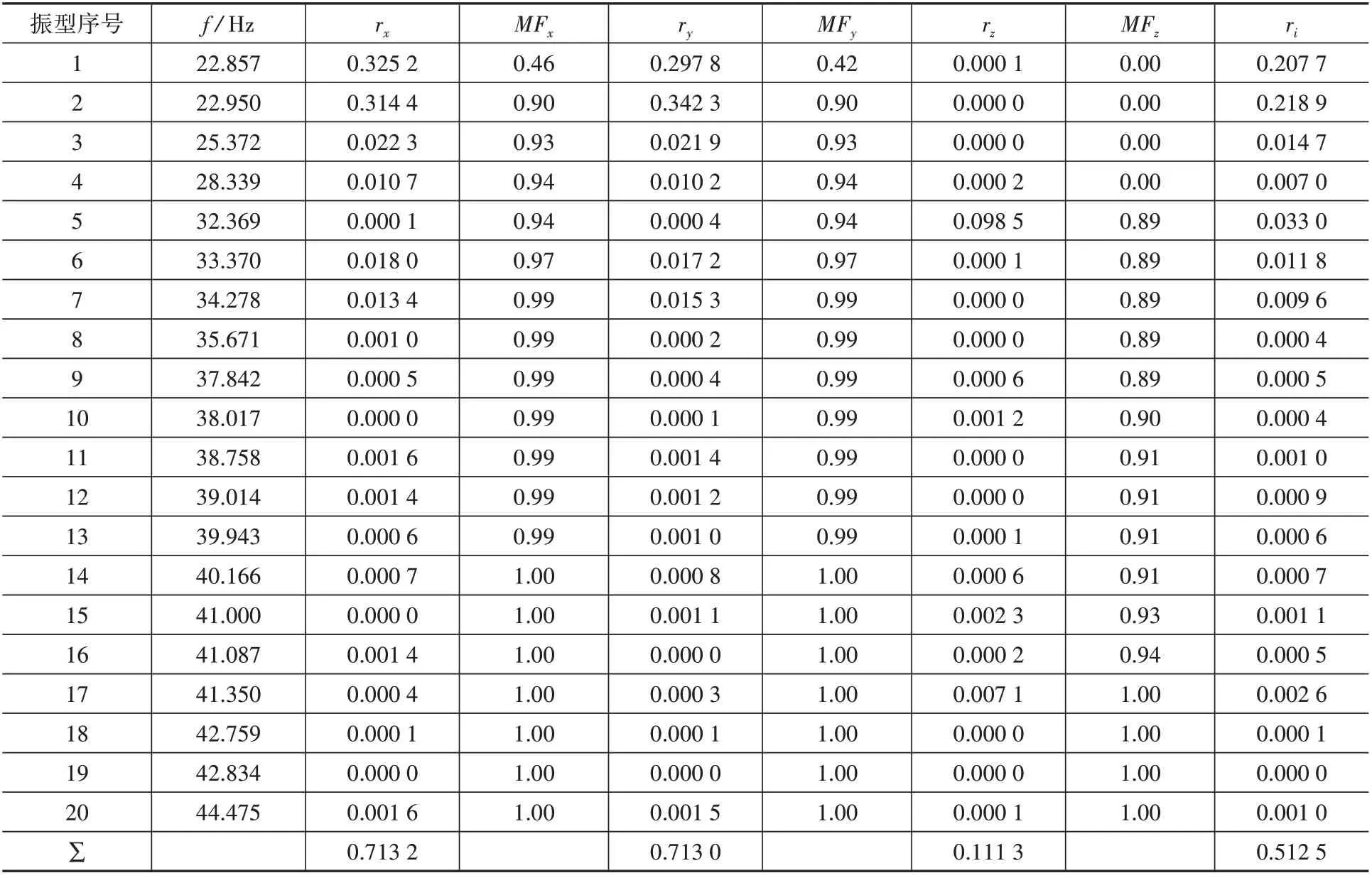
表1 频率与模态参与系数Table 1 Frequency and modal participation ratio
(3)由于边界条件的缘故,振型表现沿y=x轴线呈正对称与反对称。前6 阶振型中1、3、6 阶振型呈反对称,2、4、5 阶振型呈正对称,其中第5 阶振型较为特殊,水平振型贡献几乎为0。同时也可以看出,模态扩展阶次的确定是一个重要环节。前20 阶累计振型贡献率为0.512 5,且x、y 与z 方向累计质量分数均达到了99%以上。因此本文建议,利用反应谱分析双向张弦梁结构抗震能力时,至少应采用前17阶振型。
为直观计,图2给出了算例模型前6阶振型。
3 结构振动模态参数分析
由无阻尼结构自由振动方程可得,结构模态特性由结构质量和刚度共同决定。而影响双向张弦梁结构刚度的因素主要有下弦拉索预应力、上弦曲面矢跨比和下弦曲面垂跨比等。由于双向张弦梁结构是由三种不同受力性质构件组合而成的混合结构,其刚度受到多种因素影响,结构响应对不同参数变化的敏感性也不尽相同。

图2 1~6阶振型图Fig.2 The first 6 vibration modes
表2-表5给出了考虑大变形效应双向张弦梁结构模态特性随各参数变化的计算结果。

表2 预应力变化下的自振频率Table 2 Natural frequency in the case of the variation of prestress
由表2 可见双向张弦梁结构的低阶自振频率(1-5 阶)随预应力的增大,略微增大,但增长的幅度很小;高阶频率(6-15 阶)随预应力增大而明显增大,但增大幅度随预应力增大而略有下降。表2 中所表示的预应力为零状态时施加的预应力,经过初始形态分析计算,此预应力值明显大于初始态下弦索的轴力。考虑充分利用结构的性能与初始形态上弦曲面位移限值,双向张弦梁结构上弦一般选择刚度大截面小的构件,这也导致预应力对双向张弦梁结构自振频率影响较小。

表3 矢跨比参数变化下的自振频率Table 3 Natural frequency in the case of the variation of rise-span ratio
表3 与表4 分别为矢跨比与垂跨比参数变化下双向张弦梁结构自振频率数据。随着矢跨比与垂跨比的增大,结构自振频率随之减小,结构刚度降低。表3 中矢跨比变化范围为0/40~2/40,垂跨比变化范围为1/40~3/40,相应的自振频率变化最大差值均出现在9 阶,分别为1.652 与2.640,前15阶平均值分别为0.864与1.148。数据表明相比于矢跨比参数变化,双向张弦梁结构自振频率对垂跨比参数变化更为敏感。

表4 垂跨比参数变化下的自振频率Table 4 Natural frequency in the case of the variation of sag-span ratio
表5 表明,双向张弦梁结构自振频率随节点质量的增大而减小,其中高阶频率的减小幅度明显大于低阶频率的减小幅度。但对于相同阶数的自振频率,随质量增大,自振频率减小幅度减小。
总体而言,节点质量通过对双向张弦梁结构质量矩阵的改变进而对结构自振频率产生影响,且敏感性最高。预应力、矢跨比与垂跨比通过对结构的刚度矩阵的改变进而对结构自振频率产生影响,其中矢跨比与垂跨比参数影响较为显著,预应力参数的影响较弱。
4 结 论
通过本文中的上述分析,可以对双向张弦梁结构的自振特性得出以下结论:

表5 节点质量变化下的自振频率Table 5 Natural frequency in the case of the variation of structure mass
(1)双向张弦梁结构自振频率分布较为稀疏,存在部分阶数的自振频率十分接近的情况,基频较高,自振周期较短,结构具有良好的刚性。
(2)同时受到边界条件的影响,振型以水平方向振动为主,水平方向的模态质量参与比率远高于竖向的模态质量参与比率。
(3)参数敏感性方面,双向张弦梁结构自振频率对于节点质量参数敏感性最高,对于矢跨比与垂跨比参数敏感性一般,对于预应力参数敏感性较低。

