在小学数学教学中发展学生的提问能力

占周胜

随着课程改革的层层推进，学生的问题意识不断增强，独立思考、自主探究、合作学习、质疑反思能力不断提升。问题是打开思维的金钥匙，有了问题，学习才有方向。学生自主发现问题、提出问题更能促使他们成为一个真正的学习者，学习中会迸发出更大的创造力。在小学数学教学中发展学生的提问能力，需要转变视角，提炼核心问题;需要预留空间，生成本质问题;需要化难为易，释放关键问题。

一、转变视角，提炼核心问题

提问能力不是与生俱来的，教师要做的事应该如教育家陶行知说的：“先生的责任不在教，而在教学生学。”问题的提炼需要扣紧教材中的教学情境、问题、提示语、插图等相关信息，要读懂素材传递的学习方向以及有待解决的相关数学问题。要根据探究知识本质的需要，优化提炼新的个性问题，为学生的深入学习提供依据。

在教学“认识长方体和正方体”一课时，教材中已提出：生活中还有哪些物体的形状也是长方体？长方体有几个面？长方体有几条棱和几个顶点？它的面和棱各有什么特点？正方体有几个面、几条棱和几个顶点？它的面和棱各有什么特点？正方体具有长方体的所有特征吗？这些显性问题为学生指明了学习的方向。直接利用上述问题让学生自主学习，对于他们习得知识和能力仍然是不够的，因为通过直观感知即可获得答案会导致他们缺乏探究的源动力和意义。数学知识的获取，需要学生积极思考，需要他们主动参与到体验、探索知识形成的过程中，真正理解、掌握所学知识。因此，教师要引导学生再次深入教材，认真解读呈现的提示语、结论和基本定义。

如从图1中可以读出：长方体的面是长方形（也可能有2个相对的面是正方形），相对的面完全相同，相对的棱长度相等。

从图2中可以读出：长方体相交于同一顶点的三条棱的长度，分别叫作它的长，宽、高。

从图3中可以读出：正方体是特殊的长方体。可以用图3表示正方体和长方体的关系。

要指导学生抓住隐藏在素材背后的数学知识，根据已有的提问经验和自主学习的需要，提炼出个性化的探究问题。

（一）反问设疑，激发探究热情

提出核心问题：教材中认为，长方体的每个面都是长方形，上面和下面完全相同，是这样的吗？你有新的发现吗？你用什么方法验证？

学生根据已有经验，即可感知教材中长方体相对面特征的准确性，只是缺乏深入理解“为什么是这样”的数学活动。因此，通过设计反问质疑的方式，能够激发好奇心，使学生为了证明结论的正确性，展开深入思考、自主探究、操作说理、合作辨析，从而验证“长方体的每个面都是长方形，上面和下面完全相同”。在此过程中，学生还能发现“长方体有两个相对面是正方形，以及相对的棱长度相等”的结论。这样，就能让自主探究学习真正发生。

（二）肯定结论，探寻论证过程

提出核心问题：教材中认为，长方体的棱有3组，每组的4条棱长度相等。你是怎么理解的？说说你的想法。

棱是“新生事物”，虽然学生认识长方形的长和宽，但对棱特征的理解、归纳比较困难。为了探究目标更加明确，设计问题时，在肯定“长方体的棱有3组，每组的4条棱长度相等”的前提下，还应寻求验证棱的特征的依据，使学生在“相对棱长度相等”的基础上，通过对比、推理、操作、反思、理清知识形成的来龙去脉。

（三）联系旧知，形成知识链条

提出核心问题：正方形是特殊的长方形，那么正方体是特殊的长方体吗？请说明理由。

这样的问题能够引导学生在原有知识的基础上，回顾“正方形是特殊长方形”的推导经验，建立与新探究知识之间的实质性联系，使他们应用迁移的办法寻求证据推论“正方体是特殊的长方体”，从而获取新知识。

然后，为了给学生留下空间还可以提出另外一个问题：在自学过程中还有哪些疑惑？请写下来。这样就能为自主探究，合作学习中产生的新困惑保留机会。

问题设置要立足学生的元认知和最近发展区，采用便于学生掌握的提问策略，以“为什么”“是这样吗”“还可以怎么理解”等作为提问方式，为他们更好地应用教材发现问题、提出问题奠定基础。

二、预留空间，生成本质问题

自主探究学習并不是闭门造车，而是以问题为导向，通过自主探究学习，在基本理解、掌握知识的本质特征的前提下，更好地与同伴共同交流、探讨、辨析，阐述自己的探究过程和发现，在思维的碰撞中发现数学背后的奥秘。同时，要引导学生在自主学习、实践操作、合作交流的过程中产生新的质疑，生成新的问题。

可以提出这样的本质问题：“教材中认为，长方体有可能有两个面是正方形。有没有可能四个面是正方形呢？”“教材中认为，长方体的棱有3组，每组的4条棱长度相等。为什么我的长方体有8条棱相等呢？”“教材中认为，长方体相交一个点的三条棱的长度，分别叫作它的长、宽、高。为什么呢？”“长方体有没有两个面是梯形呢？”这些富有思维含量的探究性问题，直击长方体的本质特征，使学生通过列举、观察、操作、思辨等活动，再次将合作学习推向深入。体验自我成功解决问题的喜悦，更有利于学生对知识的理解和掌握。

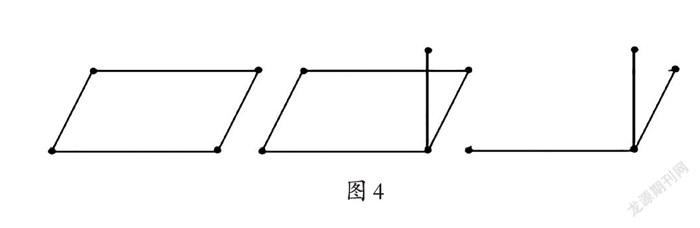
当然，当学生在学习中遇到困惑时，教师还应适当地以问题去引导他们探索知识背后的本质特征。如“为什么相交一个点的三条棱的长度，分别叫作它的长、宽、高？”可以利用活动的长方体框架，拆下一条棱启发学生思考：“你能想象出这个长方体原来的形状吗？”“再拆下两条呢？”“你觉得最少剩下几条棱还能想象出它的形状？”学生展示不同猜想，发挥空间想象能力，重构长方体原来的模型。经过生生争辩、说理、验证，最终确定：只要知道相交于一个点的三条棱的长度，即可想象出长方体原来的形状。因此，三条棱决定长方体的大小，分别叫作它的长、宽、高，从而揭示长方体长、宽、高的内在本质。（如图4）

数学学习应当是在教师的点拨下，经过学生的积极思考、合作探究、细心求证等活动理解数学知识的真正内涵。只有当学生通过自己的思考建立起数学理解力时，他们才能真正地学好数学。

三、化难为易，抓住问题关键点

在教材练习题后面，通常会根据新学知识结构和学生思维能力，搭配一道承前启后的思考题或思维拓展题。题型注重生活性、理论性、综合性，既能让学生系统地应用所学知识深入思考，又能让学生联系生活实际寻求解题思路，提升学生析题、解题能力，促进学生创新意识和创新思维能力的发展，为今后学习新知识奠定基础。虽然这类题目具有趣味性、灵活性、思想性，容易激发学生的学习兴趣和探究欲望，但是其难度系数较大，容易造成思维混乱，让学生望而却步。因此，要帮助学生分析题目，找准关键点，化难为易，搭建思维桥梁，让学生学会深入思考，探寻解题思路与方法。

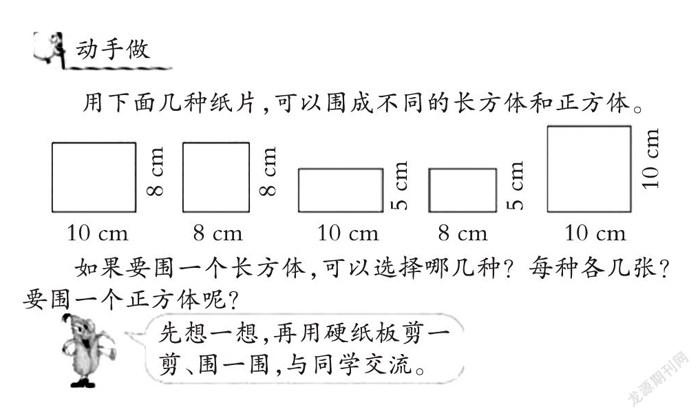
在“认识长方体和正方体”一课中的练习2后，有一道思考题是“动手做”。

题目中提供的素材和待解决的问题可选性较多，看似有很多种可能性，学生却无从下手，这也是典型的选择困难。因此，要引导学生在自主学习时善于抓住问题的关键点。例如，拼长方体的关键点在于确定底面，再根据底面的长和宽选择其它长方形进行拼接，由此对问题进行改编：

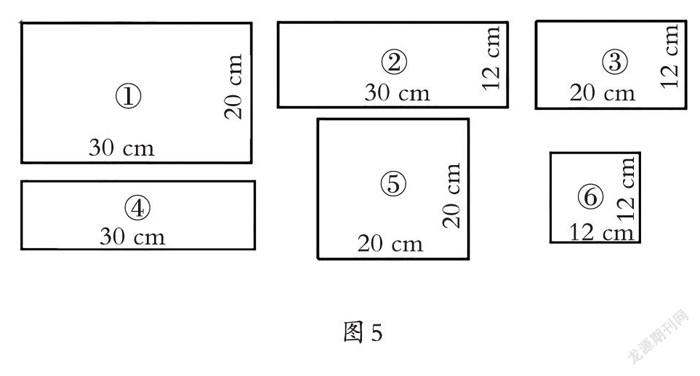
老师准备了以下几种长方形和正方形，“如果①号面为底，要围成一个长方体，你会选择几号面和它一起搭配？”（如图5）

这个问题的提出明确了學生思考的方向，剔除了干扰因素，降低了思维难度，学生的选项就显而易见了。多数学生选择①②③号面各两面或①号四面、⑤号两面，即可拼成长方体。在实践操作、解决问题中学生还会提出：“为什么不选择④号面呢？如果一定要选择④号面，可以配怎样的长方形面？”“如果任意围成一个长方体或正方体，你会怎么选择？”面对问题，他们应用长方体特征和操作经验进行推导说理就水到渠成了。

这样化难为易，再从易到难的思维过程，有利于学生在自主学习中遇到复杂问题时学会化繁为简，开启思维的匣门。随着探究的层层推进，学生的思维也会越来越逼近核心问题。这样，能使他们真正体验到“山重水复疑无路，柳暗花明又一村”的喜悦心情。

培养学生的提问能力，要在熟读教材的基础上，捕捉素材信息，变“教材”为“学材”，科学合理地设计适合自主探究的问题，引导学生深度学习。学生学到更多的提问方式和方法，能提升自主探究的学习能力，真正“会学”，为终身学习打下扎实的基础。

课题项目：本文系福建省“十三五”中小学名师名校长培养工程专项研究课题“以问题驱动小学数学深度学习的实践研究”研究成果之一。课题编号：2019XDSX046。

（责任编辑：杨强）