二维FM系统的有限频故障检测

吴小雪，刘贺平，吴慧明

（1. 北京科技大学 自动化学院，北京 100083；2. 辽宁工程技术大学 理学院，辽宁 阜新 123000）

0 引言

现代工程领域的许多问题都与二维系统密切相关，如图像处理[1]、多维信号处理[2]、多维数字滤波[3]、重复过程等[4]. 近几十年来，二维系统理论一直受到广泛关注，至今仍然是控制领域的研究热点[5-6]. 二维系统的故障检测问题更是受到广大学者的关注：文献[7]～文献[9]提出用全频方法处理二维系统的故障检测问题，然而，事实上故障一般都处在有限频域内[10]，在全频域内研究故障检测问题存在一定的保守性.近年来，有些学者考虑到这一特点研究了一系列二维系统有限频域内的故障检测问题[11-13].

由传感器掉电引起的“卡死型”故障是系统运行中常见的故障，但关于该问题的研究成果鲜见报端，且都集中在一维系统：文献[14]、文献[15]分别研究线性不确定系统和随机时滞系统的传感器故障检测问题，文献[16]研究带有传感器故障的同时故障检测与控制问题，而二维系统中具有代表意义的FM系统，其有限频域内的传感器故障检测问题并没有相关报道.

本文采用有限频H_指标和有限频H∞指标分别描述残差对故障的敏感性以及残差对扰动的鲁棒性.利用广义KYP引理，直接处理干扰和故障的有限频信息，将有限频性能指标转化为矩阵不等式条件.在处理有限频H_指标时，首先给定耦合项的上界，可以使目标变量的解集位于半径为常数的球的外部，再通过施加新的约束条件来解决该难题.本文将评估窗口定义为两个方向来反映二维向量，选择矩形区域内残差的平均值作为评价函数，可降低故障误报率.

1 系统模型

考虑如下二维离散FM模型[17]

式中，x(i,j)∈Rn为状态向量，d(i,j)∈Rnd为外部扰动输入，y(i,j)∈Rny为测量输出，A1，A2，Bd1，Bd2，C，Dd为已知的具有适当维数的常数矩阵.

考虑传感器故障中常见的“卡死型”故障, 本文定义为

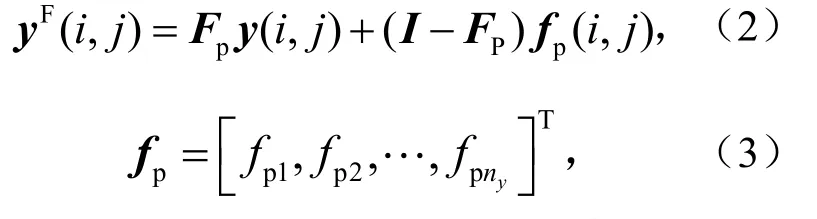
fpk(k=1,2,…,ny)可以是零或者某些未知的非零常数，表示第k个传感器的卡死值.定义

Fpk=0或者1(k=1,2,…,ny)，Fpk=0表示第k个传感器有故障，Fpk=1表示第k个传感器没有故障.

考虑式（4）中定义的传感器“卡死型”故障，可用下面模型描述系统未发生故障和系统发生故障两种情况

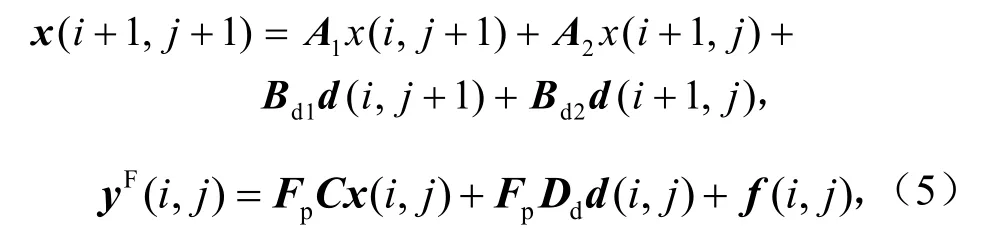
式中，f(i,j)=(I-Fp)fp(i,j).

本文目标是构造如下故障滤波器

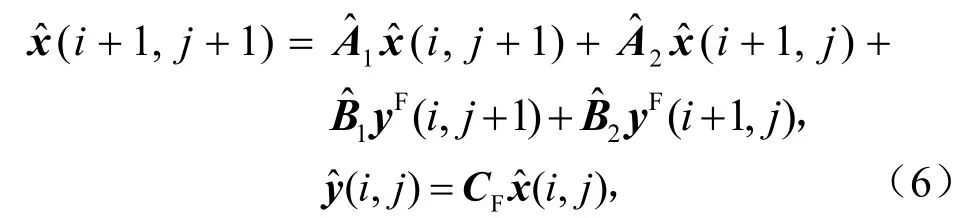
结合式（5）、式（6）可得增广系统

式中，

2 问题描述与预备知识

本文任务描述如下：对于式（1）中所表达的二维FM系统，设计式（6）的滤波器，在满足下面性能指标的情况下，且可使增广系统渐近稳定.

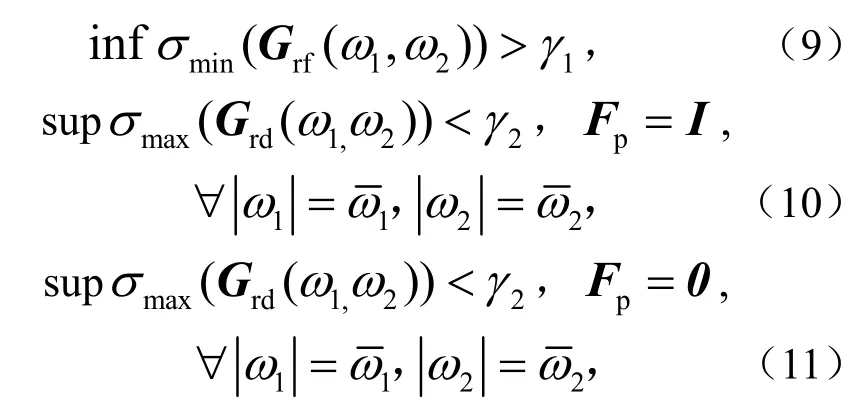
式中，1γ，2γ为给定的参数，为故障的有限频信息，增广系统从故障f(i,j)，干扰d(i,j)到残差r(i,j)的传递函数分别为

注1 为在干扰中准确地鉴别出故障，引入有限频性能指标式（9）使故障对残差的影响最大，即残差对故障敏感，参数β越大，残差对故障越敏感.同时引入性能指标式（10）和式（11），即残差对干扰有一定的鲁棒性.性能指标式（10）、式（11）分别为系统正常运行和发生故障时的鲁棒性能指标.

3 本文需用到的引理

引理1给定对称矩阵Ψ和两个矩阵Γ,Λ，存在矩阵X，满足Ψ+ΓXΛT+ΛXTΓ＜0，当且仅当以下两个等式成立

引理2假设

ξ∈Rn，P=PT∈Rn×n，H∈Rm×n，rank(H)=r＜n，则下面命题等价：

引理3对于系统1，假设对于所有(z1,z2)∈{(z1,z2)∈C×C:z1≥1,z2≥1}，都有

式中，

式中，

引理4若存在对称矩阵Ps＞0，使得

成立，则增广系统式（7）渐近稳定[21]，式中，

4 主要结果

4.1 故障敏感性条件

定理1给定标量γ1＞0，如果存在赫尔米特矩阵Pfk1、Pfk3、Qfk1、Qfk3，k=1,2，矩阵Pfk2、Qfk2、X1、X2、X3、Y1、Y2、Y3、Y4、Z1、Z2、AF1、AF2、BF1、BF2、CF满足以下各式，则增广系统式（7）满足性能指标式（9）.

式中，

证明考虑“卡死型”故障，即，取

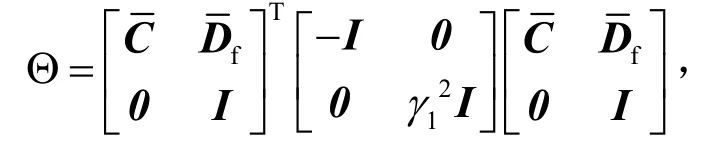
可知，若下式成立

式中，

由引理3，则

增广系统式（7）满足性能指标式（9），式（21）可改写为

式中，

令η=Λ1ξ，其中ξ为任意非零向量，则ηTΩ1η＜0，令，则有ΓTη=ΓTΛ1ξ=0.利用引理1，式（22）等价为

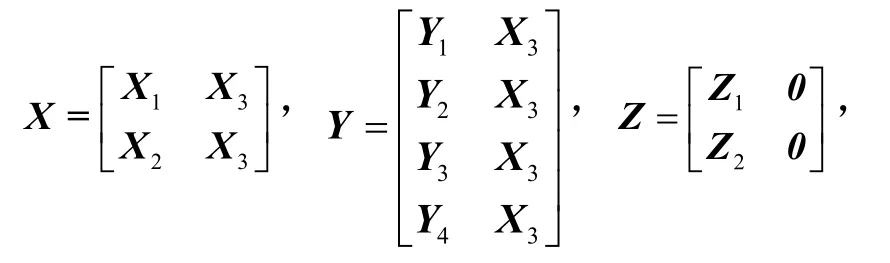
式中，

令

半径为α的球的一个切平面可由表示，则式（25）的解的凸子集可以通过式（18）求出.

4.2 干扰抑制条件

为使干扰对残差的影响最小，引入H∞性能指标式（10）、式（11）.下面给出满足性能指标式（10）、式（11）的充分条件.

定理2对于标量，假设不存在传感器故障，即Fp=1时，如果存在赫尔米特矩阵Pdk1，Pdk3，Qdk1,Qdk3，矩阵Pdk2，Qdk2，1F，2F，X3，AF1，AF2，BF1，BF2，CF满足以下各式成立，则增广系统（7）满足性能指标（10）.

式中，

Σ810=DdT.

证明由引理3，若下式成立

则增广系统式（7）满足性能指标式（10）.上式可写为

式中，

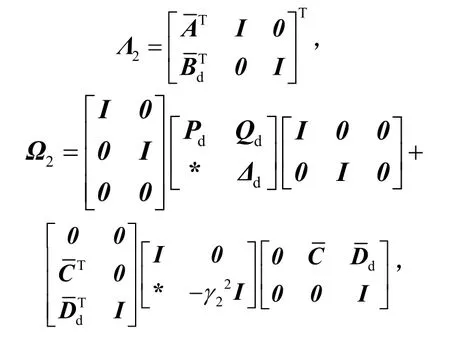
式中，

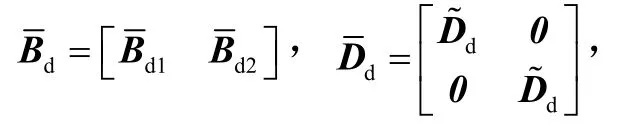
则式（28）成立.选择

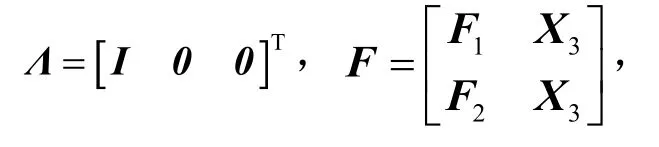
利用Schur补引理，取Fp=1，将相应矩阵代入，则为式（26）.

定理3对于标量γ2＞0，,假设存在传感器故障，即Fp=0时，如果存在赫尔米特矩阵Pmk1，Pmk3，Qmk1,Qmk3，矩阵Pmk2，Qmk2，M1，M2，X3，AF1，AF2，BF1，BF2，CF满足式（29）、式（30），则增广系统式（7）满足性能指标式（11）.

证明参考定理2证明过程.

由于广义KYP引理不包含系统的稳定性，下面分别给出当Fp=1和Fp=0时系统的稳定性条件：

定理4假设系统不存在传感器故障，即Fp=1时，如果存在对称矩阵Ps1，Ps2，矩阵Ps3，H1，H2，X3，AF1，AF2，BF1，BF2满足下式成立，则增广系统式（7）渐近稳定.

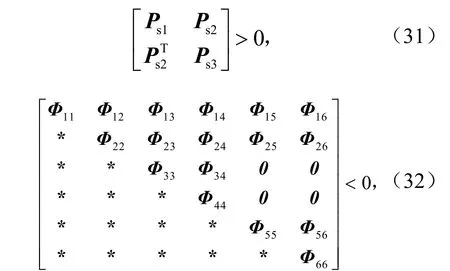
式中，

证明令，可得

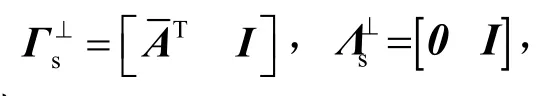
则引理4中

可以写为

又有

由引理1，可得式（33）、式（34）等价于

取

并将相关矩阵代入，可得定理：

定理5假设存在传感器故障，即Fp=0时，如果存在对称矩阵Pk1、Pk2，矩阵Pk3、K1、K2、X3、AF1、AF2、BF1、BF2满足下式成立，则增广系统式（7）渐近稳定.

证明参考定理4证明过程.

5 解决方案

下面给出求解滤波器的算法：给定实参数a，b，求解如下的优化问题

约束条件为式（17）、式（18）、式（19）、式（26）、式（27）、式（29）、式（30）、式（31）、式（32）、式（36）、式（37）.

采用文献[23]方法

式中，Jr(i,j)和Jth分别为残差函数及阈值，其中阈值的数值利用文献[24]算法求出.而对于是否发生故障，则依据如下的逻辑关系

J(i,j)＞Jth系统存在故障报警；

J(i,j)＜Jth系统无故障不报警.

6 数值仿真

考虑系统矩阵为

假设上述系统中发生了传感器“卡死型”故障，设计故障检测滤波器，在有干扰存在的状况下可有效检测系统故障.由第5节算法得到滤波器参数，

为了验证本文提出的故障检测方法的有效性，仿真结果见图1～图4，仿真中假设系统故障为

以及系统干扰

d(i,j)=0.15sin(0.5i)+0.15cos(0.5j).

系统初始状态为xi(k,1)=0，，xi(1,k)=0，，假设故障发生在低频域内，频率约束为，由文献[22]算法，可得阈值Jth=0.319 8，图1表示系统故障，图2表示系统的干扰，图3和图4分别给出了三维空间和二维空间的故障检测效果，当i等于16、24时，可以看出，J(i,j)＜Jth依据逻辑关系，系统没有发生故障，当i=34,40≤j≤150时，J(i,j)＞Jth，依据逻辑关系，系统没有发生故障.

图1 系统运行中发生的故障f(i,j)Fig.1 faults f(i,j) in system operation

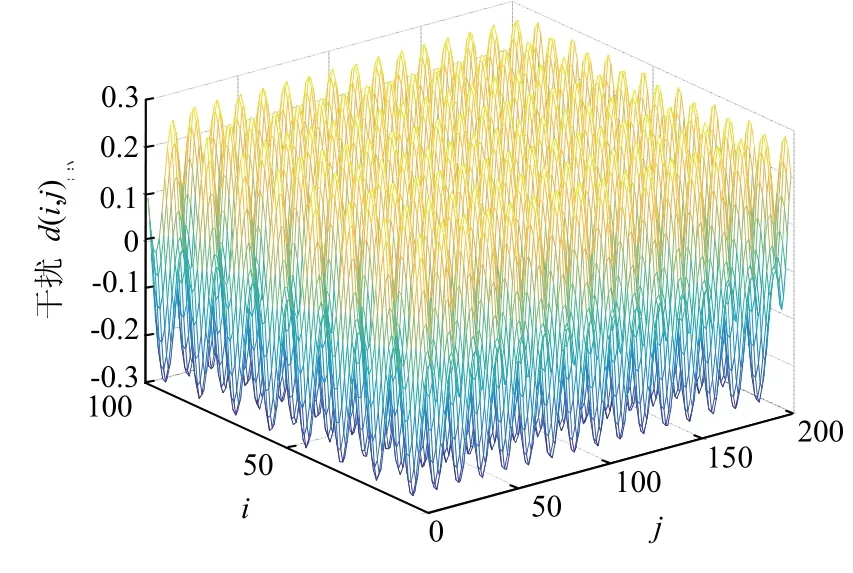
图2 系统运行中的干扰d(i,j)Fig.2 disturbance d(i,j) in system operation

图3 三维空间中的Jr(i,j)和JthFig.3 residual evalution function Jr(i,j) and threshold Jth in three-dimensional space

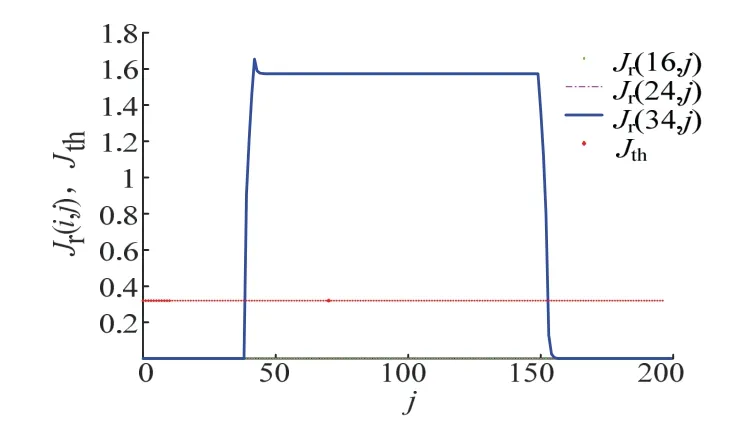
图4 二维空间中的Jr(i,j)和JthFig.4 residual evalution function Jr(i,j) and Jth in two-dimensional space

7 结论

研究具有传感器故障的二维FM系统的故障检测问题.

（1）对于系统需要满足的有限频性能指标，利用二维FM系统的广义KYP引理进行处理.

（2）该方法与频率加权方法相比，可减少运算的复杂性.

（3）利用线性矩阵不等式给出了滤波器的设计条件.

（4）数值仿真证明本文采用方法的有效性.