含水率和干湿循环对原状黄土变形特性的影响

宋 洋，刘思源，王晨炟

(1.辽宁工程技术大学 建筑与交通学院，辽宁 阜新 123000；2.辽宁工程技术大学 土木工程学院，辽宁 阜新 123000）

0 引言

黄土在中国的西北部地区广泛分布[1]，随着西部大开发战略的实施，大量铁路、公路等关乎国计民生的工程在西北黄土地区修建，由于黄土具有湿陷性的特殊变形性质，其独有的变形机理对相关工程有着不可忽视的影响，危及人身财产安全[2-4].因此，很多学者针对黄土变形的机理进行研究[5-7].武文举[8]利用英国GDS双向动态三轴试验系统对与自然沉积方向呈不同角度的原状黄土变形特征进行研究.陈开圣[9]用应变法来阐述受压变形的曲线结果，得出了一种黄土的加荷本构模型和增湿本构模型.李铮[10]通过对重塑饱和黄土分别进行静、动力三轴试验，探讨饱和黄土的静、动力特性，得出相关的经验公式.邵生俊[11]采用因子分析法，对黄土高原湿陷性黄土变形性质进行分析，研究黄土湿陷性参数和黄土地基湿陷变形精确评价的相关性.王永鑫[12]从黄土的浸水入渗特征出发，研究黄土压缩变形的特性，为相关研究提供可借鉴的方法.翁效林[13]通过对循环载荷作用下重塑黄土变形特性的研究，得出循环载荷作用下轴向和径向应变及环向和剪切应变变化幅值随主应力系数的增大先增大后减小的规律.王娇[14]利用室内试验分析了黄土的土体饱和度、土间基质吸力以及土体含水率之间的关系、得到屈服应力与基质吸力之间的变化规律.杨玉生[15]通过双线法增湿试验，对黄土在增湿条件下产生的压缩及增湿变形性质进行了研究.卢全中[16]利用三轴压缩试验，分析黄土在不同裂隙角以及不同含水量控制条件下的应力-应变关系模型，研究其变形破坏机制.

黄土具有湿陷性的特殊性质，湿陷性即黄土在一定压力下浸水后结构快速破坏引起显著地沉降变形的特性，因此黄土的含水率对黄土的性质有着重大的影响.由于天气和气候的变化，黄土土层总是受到干湿循环的影响，黄土土层的含水率始终在不断变化，随着干湿循环的作用，黄土自身的力学性质也发生了变化.大量研究表明经过干湿循环作用后的土体，呈现出土体强度减弱、土体变形变大的特点，对工程作业有着较大的影响.在针对黄土变形性质的以往的研究中，大多数学者在考虑干湿循环对黄土的影响这方面还不充分，因此本文通过原状黄土的固结试验对原状黄土在不同含水率和不同干湿循环次数条件下的应变量与割线模量之间的关系进行分析，进而研究含水率和干湿循环对原状黄土变形特性的影响.研究成果为黄土地区相关工程预测变形破坏提供科学依据，为相关研究提供借鉴.

1 原状黄土变形的试验研究

1.1 土样的获取和试验设备简介

本次室内试验所用土样皆取自宁夏回族自治区固原市西吉高速现场的原状Q3黄土，取土深度为5～6 m，土体颜色呈黄褐色，土样的获取方法如下：将包装好的原状土块平整放置，分清土样的上下层，切土方向要求与天然土层方向垂直；将切土环的内壁涂抹凡士林润滑，刀刃朝下，平整的放置在土样上.用切土刀沿着切土环向下切土，直径稍大于切土环，切成圆柱状土样，然后将切土环平整垂直的向下压，边压边削，直到土样上侧伸出切土环为止.然后将土柱根部切断，削去两端余土并沿环刀削平.擦净环刀外壁浮土，称量环刀和土样总质量，精确至 0.1 g.用削下的余土测量试样含水率.削下的试样要求与环刀紧密结合，同一组试样的干密度差值不得大于 0.03 g/cm，含水率差值不得大于 2%.将没用完的原状土密封保存，防止水分蒸发和扰动.

通过相关试验获得其各项基本物理性质指标，具体情况见表1（本文含水率指含水质量分数）.

表1 土样基本物理指标Tab.1 basic physical index of soil samples

试验采用的是直径为79.8 mm，高度为20 mm的圆柱体大环刀试样，利用三联式高压固结仪，进行固结试验，试验设备见图1.

图1 试验用三联式高压固结仪Fig.1 triple highpressure consolidation instrument for testing

1.2 不同含水率条件下的固结试验

设置5组含水率不同的试样，各组试样的含水率分别为12%、14%、16%、18%、20%，含水率相同的为一组，每组4个.

在试验开始前对试验仪器进行校准，相关操作与实际测试步骤相同，记录每级压力下的仪器误差，并在处理实际测试数据时进行调整.试验过程应确保试样受力方向与原始土层的受力方向相同.为保证同一组试验的可靠性，同一组试样之间含水率之差不应高于0.5%，密度之差不应大于0.03 g/cm3.为保证试验过程中土样中的含水量不发生变化，在放置试样后，用湿纱棉包裹压盘，避免土壤水分蒸发.

在开始试验之前，应仔细放置试件，并使其尽可能靠近仪器.然后在试件上施加一个小的预加载荷，使仪器和仪器之间紧密接触.施加第一阶段载荷后，立即移除预载.加载过程中，应注意尽量避免引起仪器振动，同时记录加载时间.载荷施加的顺序为50 kPa、100 kPa、200 kPa、300 kPa、400 kPa、600 kPa、800 kPa、1 000 kPa和1 600 kPa.根据规范的有关规定，施加相应载荷24 h之后，就可以认为黄土试样的固结变形已经稳定，可以认为是该阶段压力下试件的固结变形.通过试验，得到了不同含水率下土样的固结和压缩特性曲线.

1.3 干湿循环条件下的固结试验

考虑到实际情况，设置目标含水率接近于天然含水率（土样天然含水率平均值为16.00%，最小值为14.97%，最大值为17.02%）的3组试样，3组试样目标含水率分别设置为16%、18%、20%.每组6个试样.本试验拟采用下列方法增湿减湿.

增湿.对于有干湿循环要求的试样，需要对试样进行増湿.首先测量试样的质量及含水率，计算要达到预订含水率所需要加的水量，然后使用针管滴定试样进行加水，使试样达到预定含水率.之后，将试样放到保湿筒中静置24 h以上，使试样中水分均匀.

减湿.将静置24 h以上，试样中的水分均匀的试样自然风干，需要每隔一段时间对试样进行称量，当达到下限含水率要求的质量后，停止风干并放入保湿筒中保湿24 h以上，使试样中的水分均匀分布.

3组样品（16%、18%、20%）自然风干，每隔一段时间称重一次.当含水率达到2%时，停止风干，将样品放入保湿筒中24 h，使土样中的水分均匀分布；再滴水增湿至目标含水率，然后将试样放到保湿筒中静置24 h，保证土样中的水分均匀分布，此过程即为一次干湿循环.每组的6个试样分别循环0 次、1 次、2 次、3 次、4次和5 次.压盖板周围围上棉纱，防止水分蒸发.压力等级依次为100 kPa、200 kPa、400 kPa和600 kPa.在各压力等级下的变形速率不超过0.01 mm/h，即可认为变形达到稳定.

2 试验分析

为便于试验数据的整理和分析，对试样作出以下定义.

将试样的应变定义为

式中，Δh为试样在压应力作用下稳定后的变形量，m；h0为试样的原始高度，m.

试样的割线模量定义为

式中，ESo为垂直压应力P作用下的初始割线模量，MPa；ε为在垂直压应力P作用下的应变.

2.1 不同含水率条件下的固结试验分析

根据不同含水率试件高压固结试验获得的压缩变形数据依据式（1）和式（2），绘制不同含水率试件的垂直压缩应力应变曲线，见图2；得到了不同含水率试件的垂直压缩应力割线模量曲线，见图3.

从图2可以看出随着垂直压应力的增加，土样的应变量在逐渐增大，但增大的速率在逐渐放缓.曲线的整体形状十分接近于双曲线的形状.

从图2还能观察出，黄土试件的应变量随着含水率的提高而逐渐增加.

图2 不同含水率条件下的垂直压应力-应变关系Fig. 2 vertical compressive stress-strain relationship under different water content

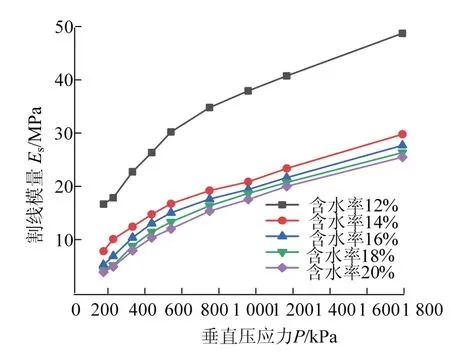
图3 不同含水率下的垂直压应力-割线模量Fig. 3 vertical compressive stress-secant modulus under different water content

从图3可以看出随着垂直压应力的增加，割线模量也呈现出增大的趋势，但增加的速度变缓，即曲线的斜率在减小.曲线还反映出在竖向载荷不大时，割线模量值变化的幅度较大，特别是在含水率较小的土样中，其值波动幅度尤为剧烈，在含水率为12%的试样中，垂直压应力从200 kPa变化到400 kPa时其割线模量Es从22.73 MPa增长到30.19 MPa，上升幅度为32.8%，垂直压应力从800 kPa增加到1 000 kPa，其割线模量从37.91 MPa增长到40.73 MPa，增长幅度仅为7.4%.这可能是因为黄土在含水率较低时，黄土土质较硬，强度相对较高，所以在含水率较低的黄土中，当竖向载荷较小时难以使土体发生压缩变形，只有当竖向载荷增加到一定程度后其压缩变形才能表现出一定的规律性.同时还可以在图3中看出曲线的整体形状与多次幂函数曲线相近从图3中还能观察出，割线模量随含水率的提高呈现下降趋势.

2.2 干湿循环条件下的固结试验分析

为研究黄土在干湿循环条件下变形的特性，对试验数据进行整理和分析，得到表2～表4.

由表2～表4可知，随着干湿循环次数的增加各级载荷下的土体割线模量均逐渐减小，以含水率为18%的试样为例：当垂直压应力为100 kPa时，土体经过各次干湿循环的作用后，其割线模量下降的幅度分别为13.8%、12.9%、11.4%、8.9%、8.3%.综合分析各组试样在不同垂直压力下经历不同干湿循环次数下的割线模量变化情况可知，各级载荷作用下土体的割线模量在1～3 次时变化幅度较大，平均下降幅度为18.2%，3～5 次之后减弱的幅度变化不大，平均降幅仅6.3%，基本趋于稳定，这表明黄土经过多次干湿循环后将达到稳定的平衡状态.

为研究含水率不同的土样经过干湿循环作用后土体割线模量的变化规律，根据表2～表4，得到了不同干湿循环次数条件下含水率—割线模量变化曲线，（以100 kPa条件下的试样为例）见图4.

表2 含水率16%试样在不同垂直压应力下各次干湿循环次数的割线模量Tab.2 secant modulus tables of 16% water content specimens under different vertical compressive stresses

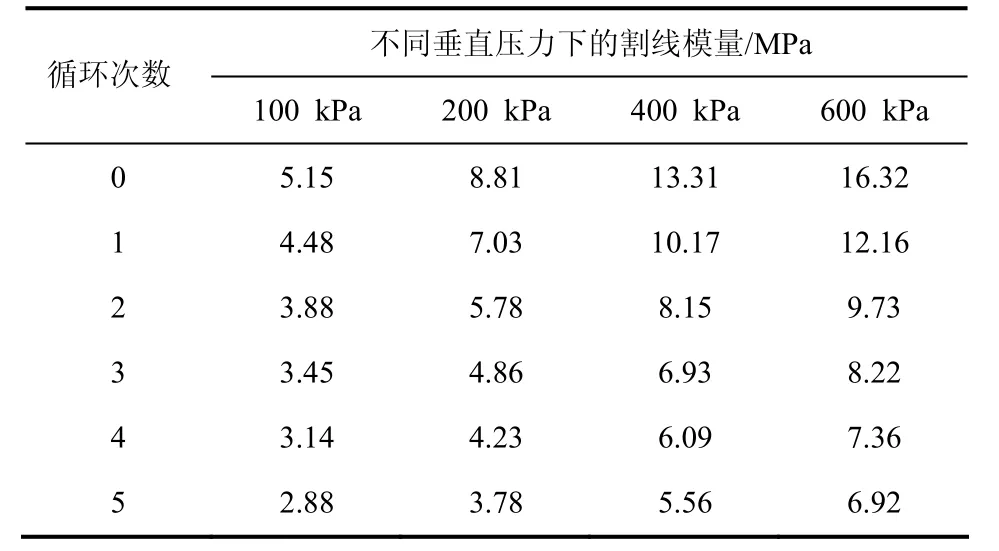
表3 含水率18%试样在不同垂直压应力下各次干湿循环次数的割线模量Tab.3 secant modulus tables of 18% water content specimens under different vertical compressive stresses

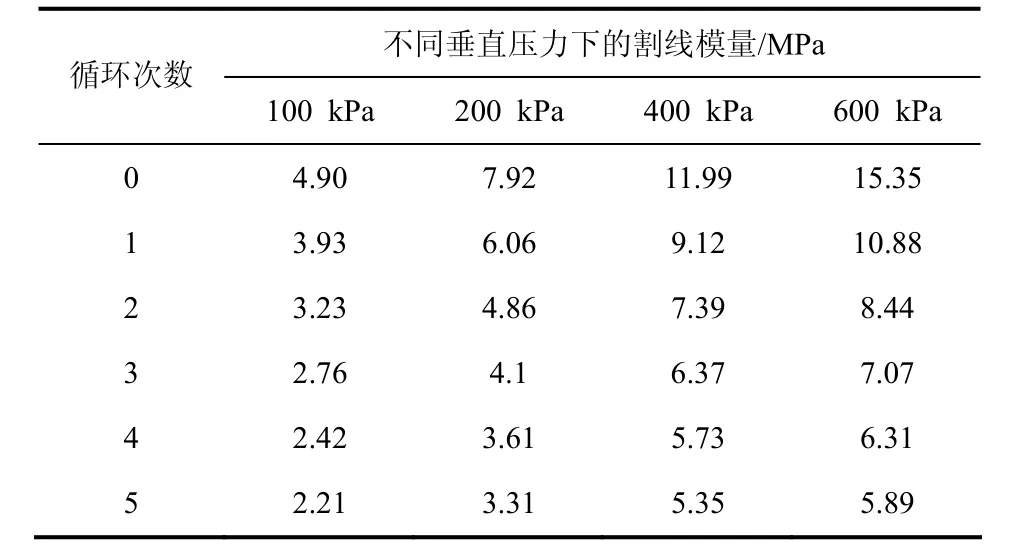
表4 含水率20%试样在不同垂直压应力下各次干湿循环次数的割线模量Tab.4 secant modulus tables of 20% water content specimens under different vertical compressive stresses

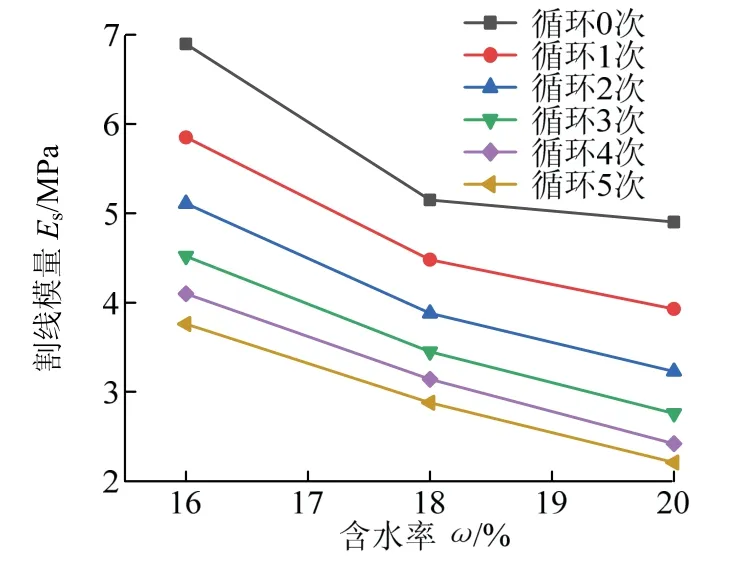
图4 不同干湿循环次数条件下含水率—割线模量Fig. 4 secant modulus change of samples with different moisture content under different drying and watering cycle index

由图4可知，土样在经历的干湿循环次数相同的条件下，仍呈现出随着含水率的升高，割线模量下降的特点，但是下降的速率随着干湿循环次数的增加逐渐趋于平缓；土样在经历3 次以上干湿循环作用后，土体的割线模量与含水率之间呈现近似于线性分布的关系，土体的割线模量几乎随含水率增加而线性地减小.

3 变形机理分析

3.1 含水率不同的黄土体的变形分析

刘保健[17]曾经对土体压缩变形研究，提出了一种割线模量分析法，该方法认为土体在外加载荷的作用下土体的割线模量与外载荷之间呈线性关系，用该法对ε-p曲线进行分析，然后通过坐标转换，将分析得出的ε-p曲线转换为P/ε-P关系曲线，即割线模量ESo与压应力P的关系曲线，其模型为

式中，P为土体所受垂直压力，kPa；Es为土体未经外力作用下的初始割线模量，MPa；B为相关模量系数，直接的斜率.

大量的试验表明，刘保健[17]利用割线模量法建立的相关模型不能完全理想的表示割线模量与垂直压应力的关系，综合考虑割线模量分析法模型的基础上，结合图2曲线的整体形状十分接近于双曲线的形状的特点及图3曲线与多次幂函数曲线的形状更为接近的特性，建立模型见式（5）、式（6），并根据式（5）对含水率不同的黄土试样其竖向压应力-应变关系曲线进行拟合分析.结果见图5.

式中，P为土体所受垂直压力，kPa；a、b、c为模量关系系数，由试验确定.

图5 不同含水率试样竖向应力-应变关系模型拟合Fig. 5 fitting of vertical stress-strain relationship model for samples with different water content

通过图5可以看出依据式（5）所建立的模型与试验数据间存在很高的契合度，现将在各曲线中拟合得到的a、b、c的数值以及相关系数等进行数整理，结果见表5.

表5 曲线拟合数据Tab.5 curve fitting data

根据表5分析得知，模量系数a、b、c与含水率ω之间存在如下关系

式中，ka、kb、kc、La、Lb、Lc为模量系数a、b、c与土体含水率ω之间的相关系数，通过试验确定.

将式（7）～式（9）分别代入式（5）和式（6），即可得到式（10）和式（11）的含水率不同的黄土的应力-应变关系模型

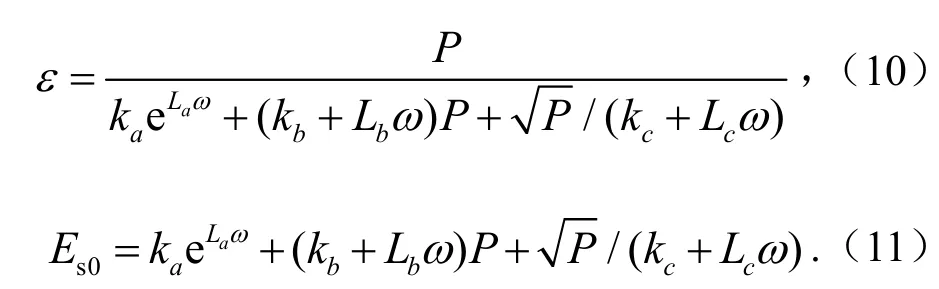
3.2 受干湿循环影响的黄土变形分析

通过对干湿循环条件下的固结试验的试验数据进行拟合分析发现，黄土试样所经历的干湿循环次数i与黄土试样的割线模量之间存在见式（1）、式（2）关系，拟合分析的结果见图6（以含水率20%的试样为例）

式中，α、β为常数；γ为负常数，α、β、γ通过试验来确定.

图6 不同垂直压应力下干湿循环次数-割线模量关系Fig.6 relation diagram of dry-wet cycle number-secant modulus under different vertical compressive stresses

3.3 干湿循环条件下确定含水率黄土的本构方程

当土体未经干湿循环即干湿循环次数i=0时，根据式（12）可得到

根据式（13）可知初始割线模量ESO=α+β，设经过i次干湿循环后的割线模量ESiO与初始割线模量ESO之间的比值为Ni，即

Ni≤1，反映了经过i次干湿循环后黄土结构的破坏程度，Ni越小黄土结构破坏的越严重.

当黄土的含水率为ω时，可根据式（10）、式（11）、式（13）、式（14）可以得到确定含水率为ω的原状黄土经过i次干湿循环的应变εi及其割线模量ESiO见式（15）、式（16）.

经过试验分析获取相应的模量系数后，即可通过式（15）求出不同垂直压应力下的应变量，进而对黄土的变形特性进行进一步研究，以含水率为20%的试样为例，将模型所求应变量与试验实测应变量进行对比，见图7.

图7 试验值与模型值的垂直压应力-应变关系对比Fig 7 comparison of vertical compressive stress-strain relation between test value and model value

由图7可知，由式（15）所得的数值解与试验所测的试验值十分接近，其最大误差仅4.9%，因此可以认为利用本文所得的本构方程模型来描述黄土试样的变形特性具有一定的可靠性.

4 结论

通过原状黄土的固结试验，系统地研究含水率、干湿循环次数以及垂直压应力对黄土变形的影响，得出以下结论：

（1）在同一垂直压应力作用下，原状黄土的应变量随着含水率的提高而逐渐增加，割线模量随含水率的提高呈现下降趋势；含水率相同的黄土随着垂直压应力的增大，其应变量和割线模量均稳定增加，但变化的速度逐渐减慢；

（2）黄土的割线模量随干湿循环次数的增多而减小，1～3次时变化的幅度较大，平均下降幅度为18.2%，3～5次之后减弱的幅度变化不大，平均下降幅度仅为6.3%，基本趋于稳定.这说明黄土经历多次干湿循环后将达到一个稳定的平衡状态；

（3）通过进行室内试验和理论分析，得出干湿循环次数i，应变εi与土体垂直压应力P和含水率ω之间的复合关系，得到干湿循环条件下确定含水率的黄土本构方程.