数控机床XY工作台单向运动二维阿贝误差分析与建模
吴天凤,李 莉,杨洪涛*
(1.安徽理工大学机械工程学院,安徽淮南232001;2.安徽理工大学矿山智能装备与技术安徽省重点实验室,安徽淮南232001)
1 引 言
直线导轨是实现高端数控机床进行平移运动的根本,精确地对直线导轨误差分析建模及补偿,是提高机床加工精度的前提[1]。数控机床XY工作台常用堆栈式结构工作台,每个方向依靠两根直线导轨共同支撑。XY工作台导轨系统误差是机床几何误差的重要组成部分,必须对其进行全面补偿才能提高机床加工精度[2-4]。
目前进行数控机床几何误差补偿考虑的由于导轨系统误差引起的工作台误差主要包括定位误差[5]、平动误差[6]和角度误差[7]等,并将这些误差代入多体系统误差补偿模型进行补偿,取得了一定效果。由于导轨系统误差不仅与导轨系统本身质量有关,而且受到运动速度、温度等参数的影响[8],X向导轨是安装在Y向导轨之上,因此在工作台导轨系统的运动过程中,Y方向导轨系统误差不仅会产生本方向上常见的线值误差和角度误差,而且还会传递至安装其上的X方向导轨系统,使其产生附加的线值和角度误差,从而产生附加阿贝误差[9],与X向导轨系统原始阿贝误差相互耦合,可见Y向导轨系统的误差影响是二维的,与工作台X向运动误差之间存在相关性和抵偿性。针对机床几何误差建模以及考虑到阿贝误差的影响,现有的国内外专家对此方向开展了许多研究。张恩忠等[10]利用激光干涉仪和温度传感器实际测量的数控机床定位误差和温度数据,建立了基于牛顿插值法和最小二乘法的几何与热复合误差建模,并根据复合模型进行了补偿实验。但利用激光干涉仪测量数据过程中,不符合阿贝原则,因此实际定位误差测量过程中会包含阿贝误差的存在,造成补偿结果不精确。赵状等[11]基于阿贝原则对齐次坐标转换矩阵的数控机床几何误差补偿模型进行了优化,并基于阿贝原则和布莱恩原则推导了阿贝误差对机床定位误差精度影响的理论计算公式,并实测机床体对角线误差进行实验验证,提高了几何误差补偿效果,但是理论推导过程中并未考虑到工作台下层导轨对上层导轨的附加影响,因此建立的阿贝定位误差模型不精确。LIU等[12]对数控机床的几何误差测量进行了研究,分析了阿贝误差的产生原理。建立了基于阿贝原理的误差模型,并通过软件补偿的方法对阿贝误差进行了补偿,从而提高数控机床的加工精度。CHEN[13]等人对传统两维工作台的定位误差补偿方法进行了研究,提出一种利用CO2激光加工的方法对机床定位误差预测和定位精度的校正。ZHONG等[14]提出一种五轴数控机床位置几何误差建模方法,建立了定位误差模型,通过使用基于递归软件的误差补偿方法对定位误差进行补偿,提高了机床定位精度。
上述学者关于基于阿贝原则的机床几何误差建模以及定位误差补偿的研究中,基本上只考虑单一方向的导轨系统引起的阿贝误差,造成机床误差补偿效果有限,因此本文对温度作用下的数控机床XY工作台单向运动二维阿贝误差的变化规律、传递机理和建模方法开展研究。
2 数控机床XY工作台导轨系统误差源及相关性分析
2.1 导轨系统误差源分析
数控机床目前经常采用的是堆栈式结构XY工作台,如图1所示。X方向导轨通过溜板安装在Y方向导轨之上,工作台则安装在X导轨溜板的上面,待加工的工件则放在工作台上[15]。每个方向导轨系统在运动过程中均存在六项几何误差,包括三项平动误差和三项转角误差[16]。当导轨沿X方向运动时,三项平动误差包括定位误差σxx和Y方向上的直线度误差σxy和Z方向上的直线度误差σxz。三项转角误差包括偏摆角误差εxz、俯仰角误差εxy、滚转角误差εxx(误差符号下标的第一个字母表示运动的方向,第二个字母表示误差产生的方向)如图2所示。在温度作用下,每项几何误差分量会产生附加热误差,包括偏摆角热误差俯仰角热误差和滚转角热误差因此每项误差分量分别是原始误差分量、附加热误差的叠加。
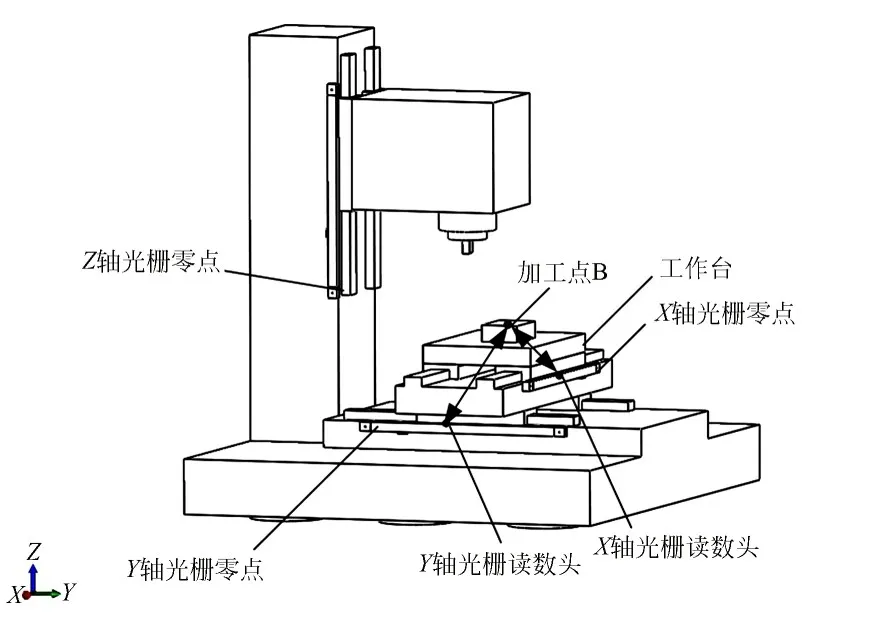
图1 数控机床工作台结构示意图Fig.1 Structure diagram of CNC machine tool table
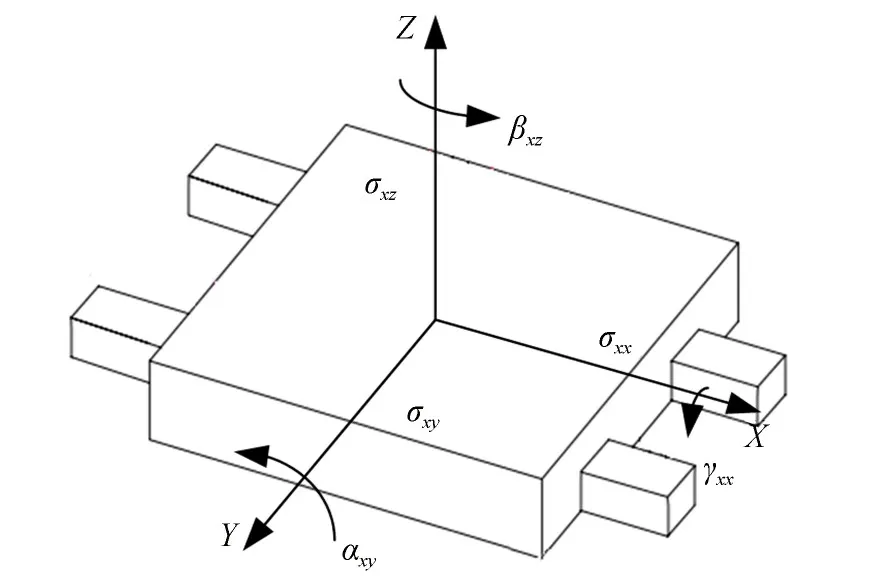
图2 三轴机床X向导轨移动副6项误差示意图Fig.2 Schematic diagram of the six errors of X axis
2.2 XY工作台导轨系统误差相关性分析
2.2.1Y轴导轨系统单向运动Y方向误差分析
设工件待加工点在XY工作台上的理想位置坐标为B(x,y),X和Y向导轨上的光栅安装位置如图1所示[17]。设X,Y轴光栅测量系统的读数头与零点之间的距离分别为x,y。当工作台沿着Y轴单向运动时,Y轴导轨存在由于机床制造精度等原因产生的几何误差,将相应的线值和角度误差分别用和俯仰角偏摆角滚转角表示。由于温度变化的影响[18-21],Y向导轨也存在了附加热误差:俯仰热误差偏摆热误差滚转热误差因此Y轴导轨系统单向运动时的各误差分量分别是上述原始误差、附加热误差的矢量和。
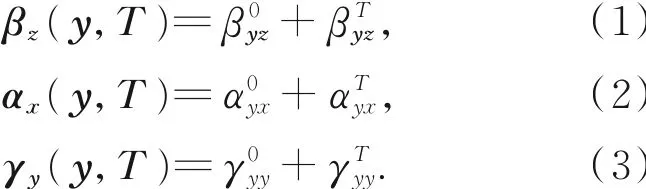
2.2.2Y轴导轨系统单向运动各误差分量对X轴导轨误差相关性分析
因为堆栈式XY工作台的特殊结构,X轴导轨系统安装在Y轴导轨系统上,所以在X轴导轨运动的过程中,Y轴导轨系统误差会通过溜板结构传递至上层结构,引起X方向导轨产生相应的各种附加误差,因此下面分析X轴导轨系统各项误差的特性和计算公式。
由上述分析可知,X轴导轨系统自身同样存在了Y轴导轨系统类似的三项线值误差σxx,σxy,σxz,和三项角度误差,俯仰角偏摆角滚转角包括由于温度影响引起的附加热误差X轴导轨系统三项线值误差不受Y轴导轨系统的影响,但是Y轴导轨系统角度误差会传递到X轴导轨系统,因此X轴导轨系统的综合偏摆角βz(x,y)等于X轴导轨系统自身偏摆角和Y轴导轨系统偏摆角的矢量和。
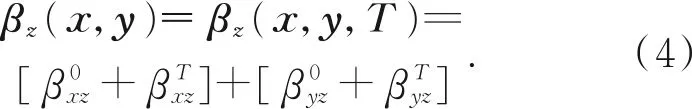
同理,X轴导轨系统的综合俯仰角αx(x,y)等于X轴导轨系统自身俯仰角和Y轴导轨系统滚转角的矢量和。
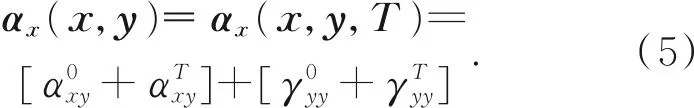
同理,X轴导轨系统的综合滚转角γx(x,y)等于X轴导轨系统自身滚转角和Y轴导轨系统俯仰角的矢量和。
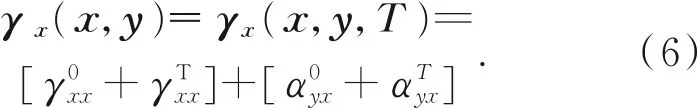
3 导轨系统误差引起的XY工作台阿贝误差建模
3.1 阿贝偏移分析
在以光栅尺为位置控制单元的机床上,运动轴的位置是靠光栅测量系统实时反馈得到的,光栅尺的位置作为基准测量轴线[11]。在XY工作台误差测量的过程中,从图1可知,Y轴光栅尺的基准线与待加工工件所在的测量线不在同一条直线上,不满足阿贝原理[22],因而存在阿贝误差[23-24]。待加工点B与Y向光栅测量系统之间的阿贝偏移关系如图3(a)所示,其中测量点B与光栅零点之间的直线距离为沿Y轴导轨运动时的阿贝偏移大小。设Ax为该阿贝偏移在X方向上的分量大小,由机床的结构分析可知,Ax与加工点B的X坐标相关。同理Az为其阿贝偏移在Z方向上的分量大小,其与加工点B的Z坐标相关。
同理,待加工点B与X光栅测量系统之间的阿贝偏移如图3(b)所示。By为该阿贝偏移在Y方向上的分量大小,与加工点B的Y坐标相关。BZ为其阿贝偏移在Z方向上的分量大小,其与加工点B的Z坐标相关。
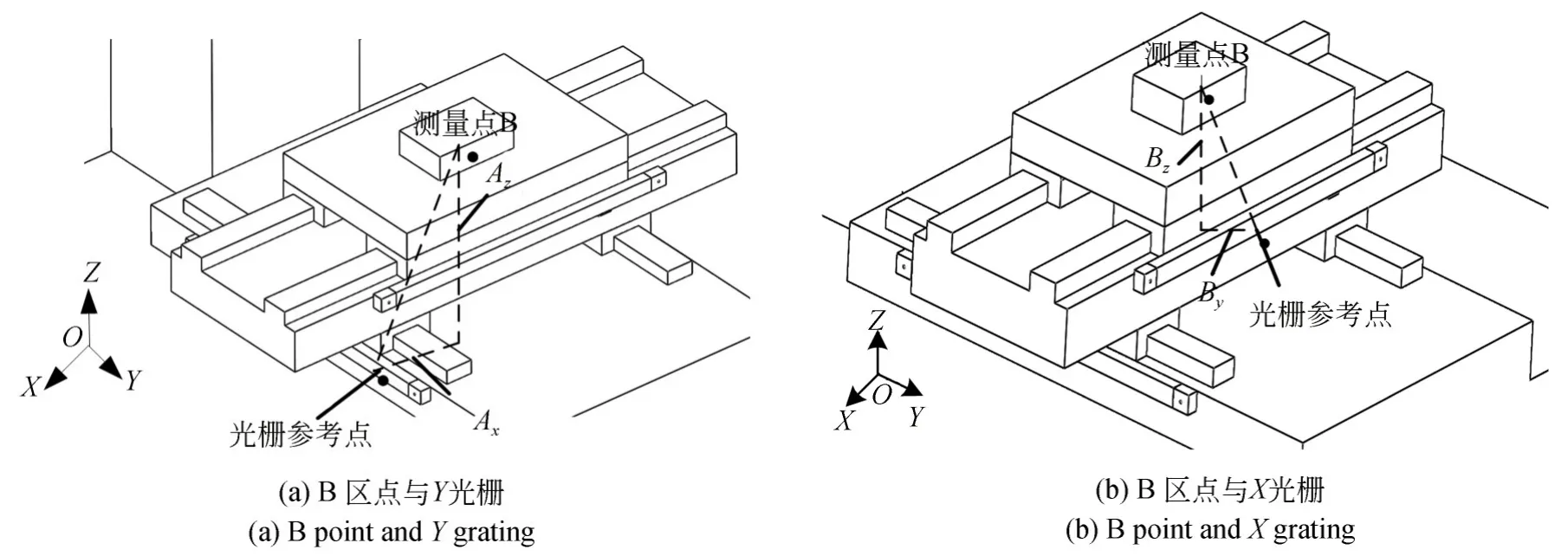
图3 B点和光栅测量系统之间阿贝偏移示意图Fig.3 Abbe offset diagram between point B and grating measuring system
3.2 阿贝误差计算
3.2.1Y轴导轨单向运动一维阿贝误差建模
在上述分析的Y向导轨系统俯仰和偏摆综合角度误差作用下,测量点B在Y向的阿贝误差包括两个分量δpy和δfy,其与对应的阿贝偏移与角度误差关系如图4所示。
从图4(a)可知,Y轴导轨系统原始偏摆角β0yz和B点X方向上的阿贝偏移Ax联合作用产生的偏摆阿贝误差δpy可利用式(7)计算:
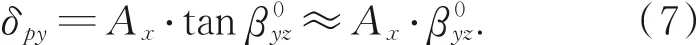
从图4(b)可知,Y轴导轨系统原始俯仰角和B点Z方向上的阿贝偏移Az联合作用下产生的俯仰阿贝误差δfy可利用式(8)计算:
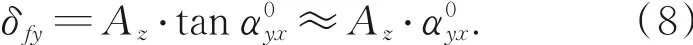
因此由偏摆阿贝误差δpy和俯仰阿贝误差δfy联合作用下的待加工点B在Y方向的阿贝误差δy1为:
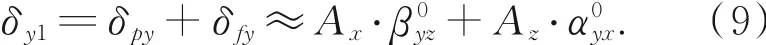
同理分析可知,在温度综合影响下的Y轴导轨单向运动一维阿贝误差模型为:
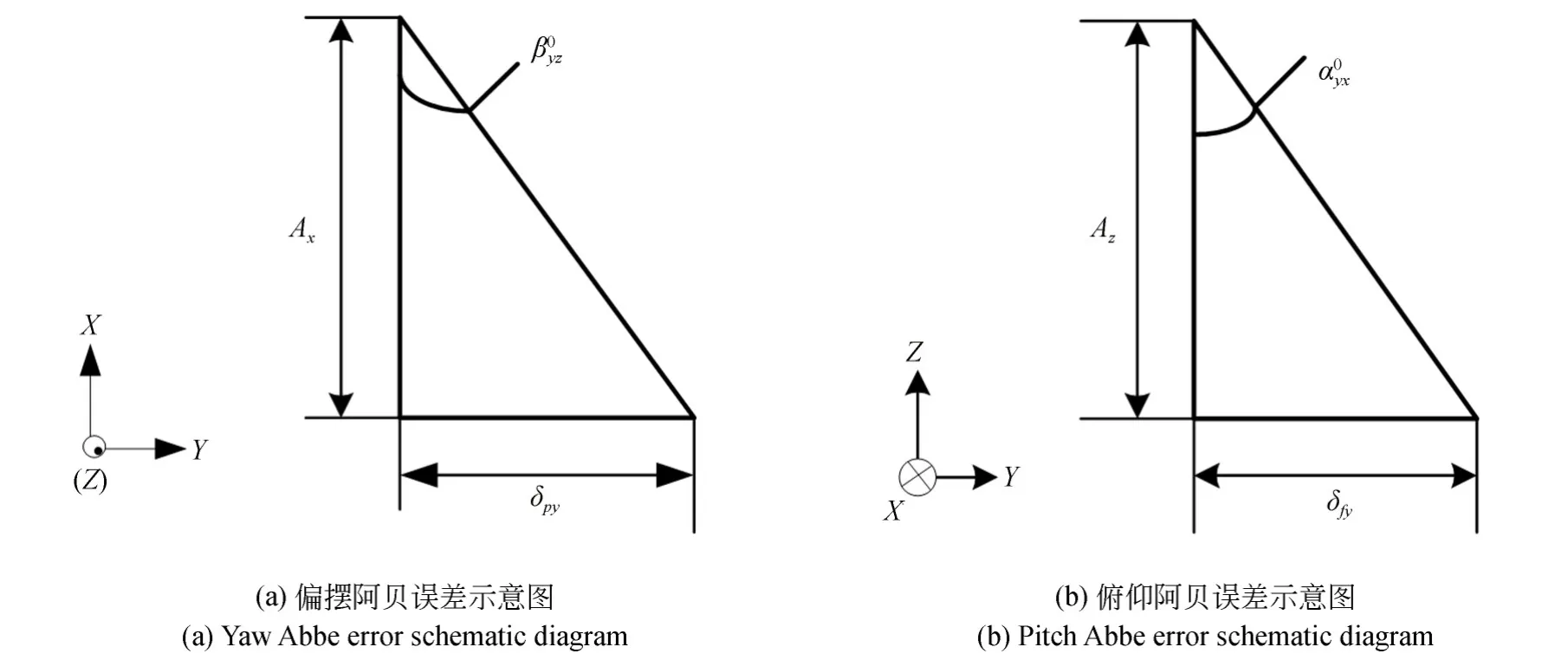
图4 待测量点B点沿Y导轨方向的阿贝误差示意图Fig.4 Abbe error diagram of point B to be measured along the Y guide rail
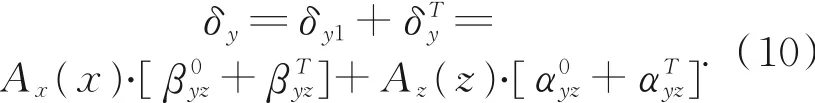
3.2.2X轴导轨系统二维阿贝误差建模
从图5(a)可知,X向偏摆阿贝误差δpx是由X轴导轨系统偏摆角βz(x,y)和加工点B在Y方向阿贝偏移联合作用的结果,如图5(b)所示X向俯仰阿贝误差δfx是X轴导轨系统俯仰角αy(x,y)和加工点在Z方向阿贝偏移联合作用结果。
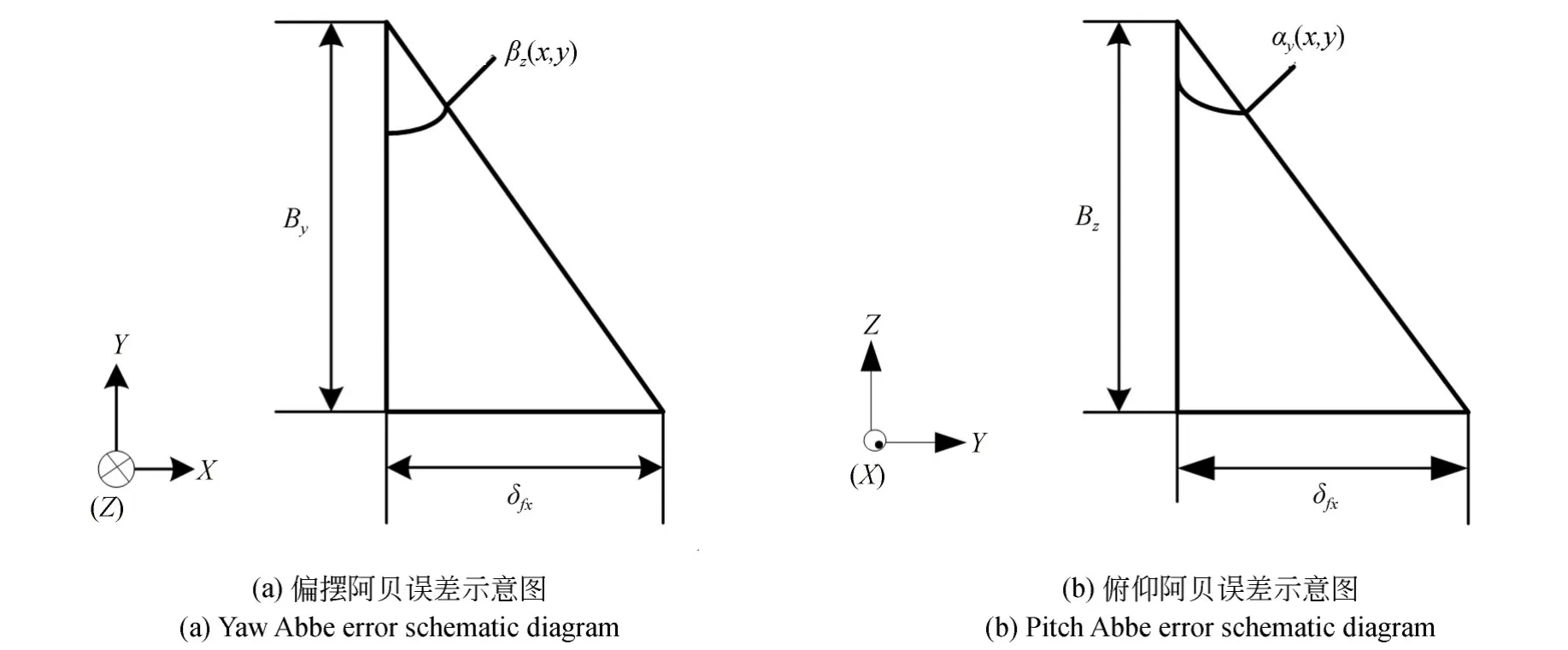
图5 B点沿X导轨方向阿贝误差示意图Fig.5 Abbe error diagram of point B to be measured along the X guide rail
在温度综合影响下的Y轴导轨系统误差对X轴导轨系统二维阿贝误差模型为:
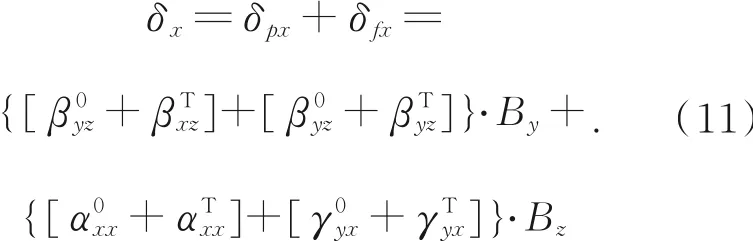
4 实验验证
4.1 XY工作台导轨系统角度误差相关性验证
从2.2节可知,XY工作台X轴导轨的角度误差不仅与X轴导轨自身的角度误差有关,而且与Y轴导轨角度误差相关。为了验证XY工作台沿X,Y轴导轨运动时角度误差的相关性,由于实验条件的限制,实际机床的控温操作难度较大,因此本文实验部分暂时未考虑温度作用下的导轨系统角度误差相关性影响,只着重于考虑在正常环境温度下的角度相关性分析。下面以X轴导轨系统偏摆角为例进行实验验证。

图6 误差测量实验装置图Fig.6 Experimental device for error measurement
本文以TONMAC数控铣床为实验对象,利用RenishawXL-80双频激光干涉仪[25]测量机床工作台沿X轴、Y轴导轨单独运动时和X,Y轴导轨系统45°对角线方向上联动时的X轴偏摆角度[26],所搭建的实验装置如图6所示。图6(b)显示的是工作台沿着X方向和Y方向同时运动时的偏摆角测量装置,即激光干涉仪的参考镜和反射镜安装在工作台运动的45°对角线方向上。根据所测量的机床工作台实际行程限制,设置工作台的测量行程为150 mm,采样的间距为5 mm,上述三种运动模式下每种行程重复测量三次,取三次平均值作为最终误差测量结果,误差曲线如图7所示。将测量得到的X轴导轨和Y轴导轨运动时的偏摆角按照式(4)进行矢量和,计算得到Y轴的相关性综合偏摆角误差曲线如图7所示,可以看出,Y轴导轨系统的综合偏摆角整体上与工作台X,Y轴联动测量的X轴偏摆角相比,误差呈下降趋势,且最大差值达到0.92弧秒(arc sec),可以证明公式(4)的准确性。同理可以证明X轴导轨的俯仰角和滚转角计算公式(5)和(6)的准确性。
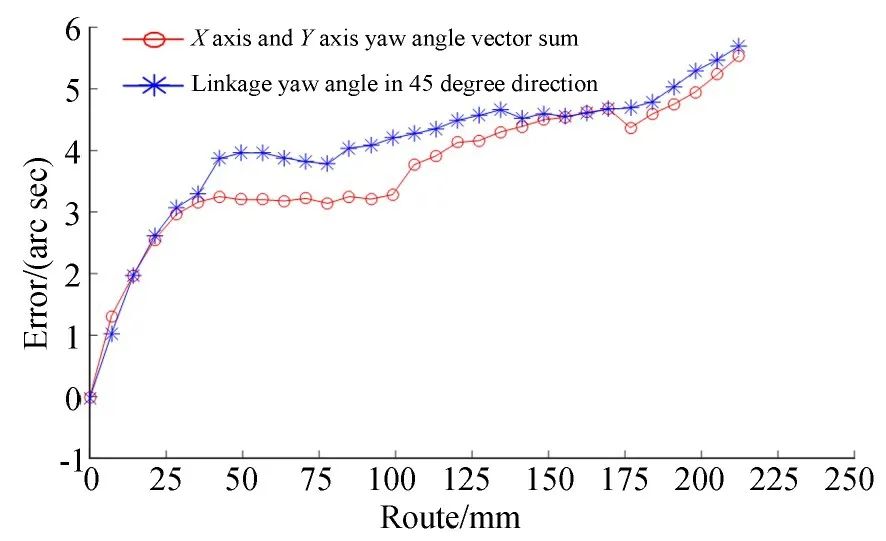
图7 X导轨偏摆角相关性验证图Fig.7 X guide rail yaw angle correlation verification diagram
4.2 工作台二维阿贝误差修正效果验证
为了比较由于工作台二维阿贝误差对工作台定位误差的影响,本文利用XL-80双频激光干涉仪测量XY工作台导轨沿对角线45°方向上联动的定位误差和联动偏摆角,再分别测量出X轴导轨的偏摆角、俯仰角和Y轴导轨的偏摆角和俯仰角,测量行程和采样间距与4.1节测量过程保持一致。
首先对测量得到的工作台定位误差进行传统的阿贝误差补偿,即在联动定位误差的基础上减去相应偏摆角、俯仰角与对应阿贝偏移的乘积,补偿结果记为补偿后定位误差1;同理,利用误差相关性和二维阿贝误差对定位误差进行阿贝误差补偿,即在联动定位误差的基础上减去联动偏摆角与阿贝偏移的乘积以及Y轴导轨偏摆角、俯仰角与其对应阿贝偏移的乘积(公式(11)),补偿结果记为补偿后定位误差2,结果如图8所示。
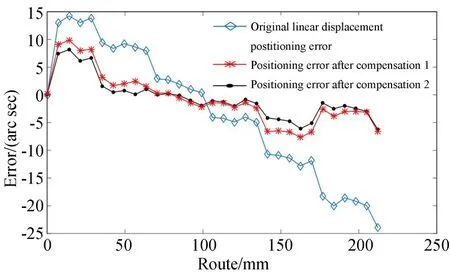
图8 导轨系统阿贝误差修正对比图Fig.8 Abbe error correction comparison diagram of guide rail system
从图8中可以看出,利用工作台二维阿贝误差补偿后的定位误差2整体误差呈减小趋势,且比用传统方法补偿后的定位误差1最大相差3 μm左右,占补偿后的工作台总误差的三分之一,补偿效果更好,因此本文建立的工作台二维阿贝误差补偿模型更符合工作台实际的误差分布特点和规律。
5 结 论
本文详细分析了数控机床XY工作台导轨系统误差源和Y轴导轨系统单向运动各误差分量对X轴导轨误差相关性,建立了XY工作台Y轴导轨系统误差和上层X轴导轨系统误差相关性模型,从中可以得出,X轴导轨系统综合偏摆角是X轴导轨自身偏摆角和Y轴导轨偏摆角的矢量和,X轴导轨综合俯仰角是X轴导轨自身俯仰角和Y轴导轨滚转角的矢量和,X轴导轨综合滚转角是X轴导轨自身滚转角和Y轴导轨俯仰角的矢量和。
建立了Y向导轨系统的阿贝误差和X向导轨系统二维阿贝误差计算模型,分别进行了X轴导轨和Y轴导轨角度误差相关性验证和导轨系统定位误差补偿效果对比实验。实验结果证明利用工作台二维阿贝误差补偿后的定位误差2整体误差呈减小趋势,且比用传统方法补偿后的定位误差1最大相差3μm左右,占补偿后的工作台总误差的三分之一。本文所建立的导轨系统二维阿贝误差模型更符合数控机床XY工作台误差的实际变化规律,利用该模型导轨进行的工作台联动定位误差补偿效果比传统补偿方法的修正效果更好,为提高机床加工精度和在机测量系统的测量精度打下理论基础。

