基于FPGA的EMD算法实现方法的研究
周 浩,段欣欣,闵康磊,蒋志胜,李 金
(上海航天电子技术研究所,上海201109)
在机械动态分析、设备状态检测与故障诊断过程中,存在着大量的非平稳信号。对于非平稳、非线性信号比较直观的分析方法是,使用具有局域性的基本量和基本函数,经验模态分解EMD 算法是由N.E.Huang 等人提出的一种将信号分解成特征模态的方法[1-2]。在结构动力分析、医学检测、地震检测以及设备故障诊断等工程领域,EMD 算法具有重要的意义。
随着FPGA 技术的成熟,越来越多的嵌入式设备选择围绕FPGA 为处理核心建立。在此,通过研究基于FPGA 平台EMD 算法的实现方法,有利于EMD 算法以及HHT 算法的平台移植,有利于故障检测等仪器设备向小型化、便携式方向发展。
1 EMD 原理及FPGA 技术
EMD 算法的优点是不会运用任何已经定义好的函数作为基底,而是根据所分析的信号来自适应生成固有模态函数,可以用于分析非线性、非平稳的信号序列,具有很高的信噪比和良好的时频聚焦性。因此基于EMD 方法的机械故障诊断方法广泛应用于各个工程领域。
EMD 信号分解方法是一种具备自适应能力的信号时频分析方法,能够根据信号本身的特性,抽取被处理信号的固有模态函数,是能够应用于非线性非平稳信号的分析方法[3]。该方法将原始待处理信号分解为多个窄带信号分量,该窄带分量被称为本征模态函数(IMF),本征模态函数为单分量信号,该信号能够描述具有实际物理意义的瞬时频率。
1.1 EMD 算法实现条件
IMF 函数必须符合2 个条件[4-5]:IMF 信号序列中,极值点的数量和零点数量相差不能大于1;整个信号函数任意点上,上下包络的均值必须为0。
对此,EMD 算法实现必须满足3 个条件[6]:①原始信号函数中至少需要包含2 个极值点(1 个最大值和1 个最小值);②信号序列的局部时域特性必须仅受极值点的时间尺度影响;③当信号序列只包含拐点时,可通过微分获得极值。
1.2 EMD 算法分解原理
EMD 方法分解流程如图1所示。
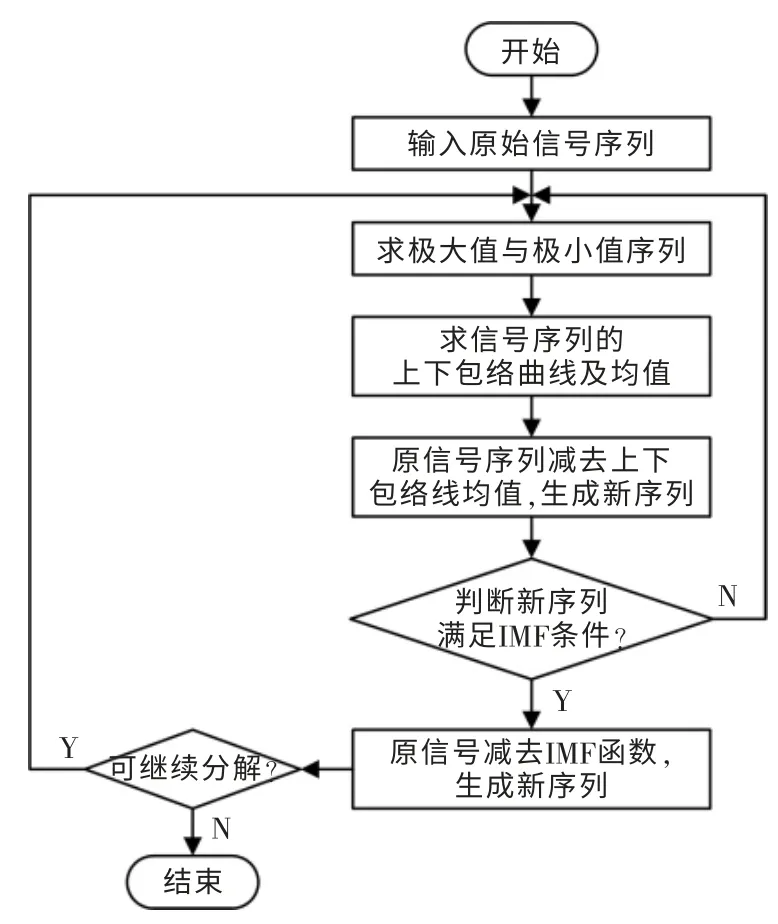
图1 EMD 分解流程Fig.1 EMD decomposition flow chart
步骤1确定原始信号序列x0(t)中的极大值与极小值;
步骤2利用三次样条插值方法,计算获得原信号函数包络线函数ysup(t),yinf(t),并计算上下包络线函数的均值y0(t)。即

式中:ysup(t)为上包络线;yinf(t)为下包络线。
步骤3由于信号序列中,上下包络线的均值为信号中的低频分量,利用原始信号序列减去上下包络线的均值序列,构建新的待分解信号序列。即
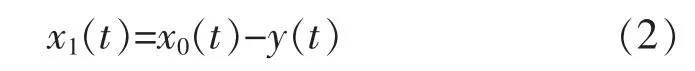
步骤4重复以上步骤,直至新的信号序列满足IMF 函数条件,获得IMF 函数,即为当前信号序列的最高频率分量:
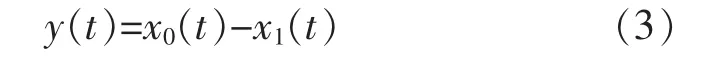
步骤5原信号函数x0(t)减去IMF 函数,得到新的信号函数x0(t),重复以上步骤,直至新的函数x0(t)不可分解为止。
1.3 FPGA 技术
现场可编程门阵列FPGA 使用预建的逻辑块和可重新编程布线资源,用户无需再使用电路试验板或烙铁,就能配置这些芯片来实现自定义硬件功能。用户在软件中开发数字计算任务,并将其编译成配置文件或比特流,其中包含元器件相互连接的信息。此外,FPGA 可完全可重配置,当用户在重新编译不同的电路配置时,能够当即呈现全新的特性。FPGA 运行处理快,同时具有丰富的逻辑资源以及专业IP 资源,基于FPGA 的嵌入式系统开发,便于功能拓展和设备模块自定义处理。
2 EMD 算法的FPGA 实现方法研究
通过分析EMD 算法原理,在FPGA 实现过程中,包括极值点计算和上下包络线序列计算,2 个核心步骤。
2.1 三次样条插值算法实现
在此,选择三弯矩算法求解上下包络线。根据定义,设待插值序列为
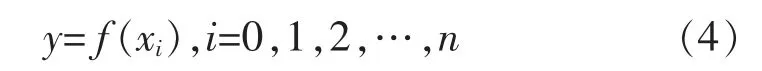
设三次样条函数S(x)为

设S(x)的二阶导数为
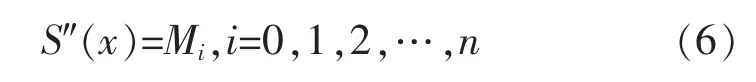
根据拉格朗日插值定理,可知

利用2 个定点xi和xi+1,可求得
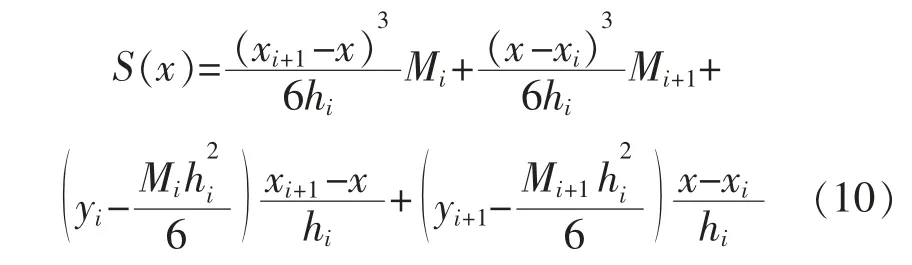
经过数学化解,并记作
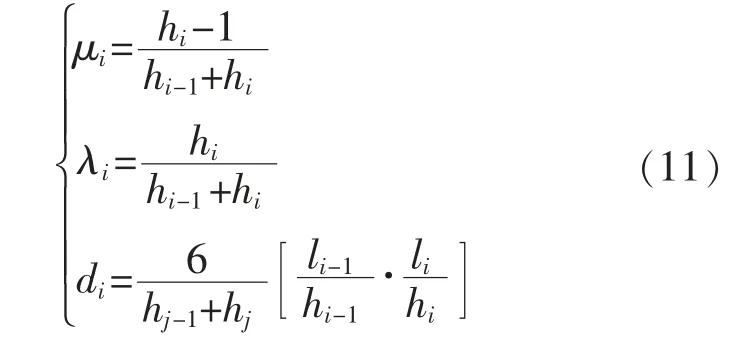
将方程(10)简化为
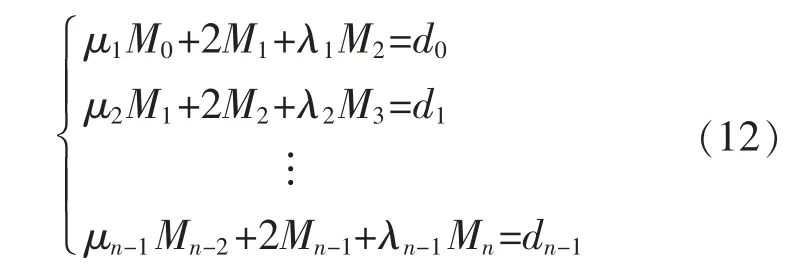
补充边界条件,令

得到矩阵:

由式(11)可知,μ 和λ0的值均<1,故矩阵满足:

矩阵(14)能够采用TDMA(the tridiagonal matrix algorithm)进行求解。具体如下:
其一,通过前向消元,将原矩阵转换为上三角矩阵。即

其中
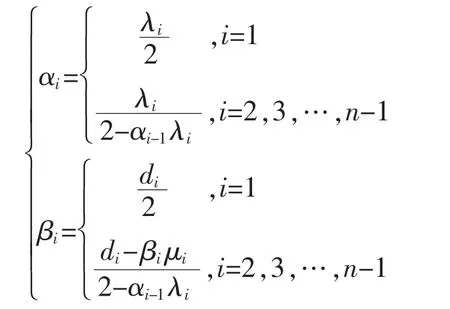
其二,逆向求解。即

其三,求解参数。即

2.2 FPGA 实现流程
EMD 信号FPGA 实现流程如图2所示。FPGA进行EMD 分解时,首先FPGA 器件将需要处理的数据由数据存储芯片读取到DDR2 芯片中,用于数据缓存。然后,将RAM 中的数据采用只读的方式读取到原始信号暂存模块。
极值求解模块实现流程 ①通过FPGA 将接收到的待处理原始信号序列放入RAM 中;②依次读取原始信号序列中的值,分别放入寄存器ABC 中;③数值比较模块读取寄存器中的值并进行比较,经过比对确定寄存器B 是否为极值,如果是则触发极值步进计数,并写入极值FIFO,识别极值属于极大值或极小值分别写入相应的缓存FIFO 中,在极值状态寄存器中标识极值类型,对寄存器B 的值进行零点判决,对零点进行识别并缓存标识;④一次数据比较完成(1 个时钟周期)后,寄存器中的值由寄存器C 传递至寄存器A,寄存器C 从原始信号缓存区(RAM)读取下一个值。
当原始信号序列缓存FIFO 变为“空”状态时,完成一次极值序列求解过程。极值序列求解完成后进入上下包络求解模块,开始进行执行三次样条插值程序。
三次样条插值模块 考虑到上下包络线序列计算方法相同,利用FPGA 器件并行处理的特性,同时执行上下包络线序列计算。由于上下包络线求解过程一致,同步进行上下包络线函数求解。三次样条插值模块遵循着尽量使用加法器进行运算,减少乘法器使用的规则。
该模块包括函数因子计算和插值点值计算两部分。函数因子计算部分 ①根据式(7)(8)(11),计算hi,li,μi,λi,di;②计算矩阵,获得二阶倒数因子Mi;③根据式(18),求解每个插值点的值。插值点值计算部分 求解插值点的过程中读取极值初始寄存器的值,如果寄存器值为高电平(第1 个极值为极大值),则读取步进FIFO 中数据偶数位(0,2,…)为极大值步进,奇数位(1,3,…)为极小值步进,反之,交换读取方式。
采用倒序读取的方式,设置步进计数器,获得2个极值点件插值点的数量,在上下包络FIFO 中写入极值点和插值点的数量。将单次使用的计算因子写入到FIFO 中,需要重复使用的因子写入FPGA例化的RAM 模块中。
将计算得到的函数序列进行IMF 函数条件验证。该过程有2 个步骤:①分别读取极值计数寄存器的值和零点计数寄存器中的值,判断是否满足IMF 函数条件1;②计算相对应极大值与极小值的差值,判断上下包络线均值是否为0,函数序列是否满足IMF 函数条件2。根据验证结果,如果生成序列满足IMF 条件,则输入到下一级,用于后期信号处理;否则,用原始函数序列减去相应值,重复执行之前的操作。
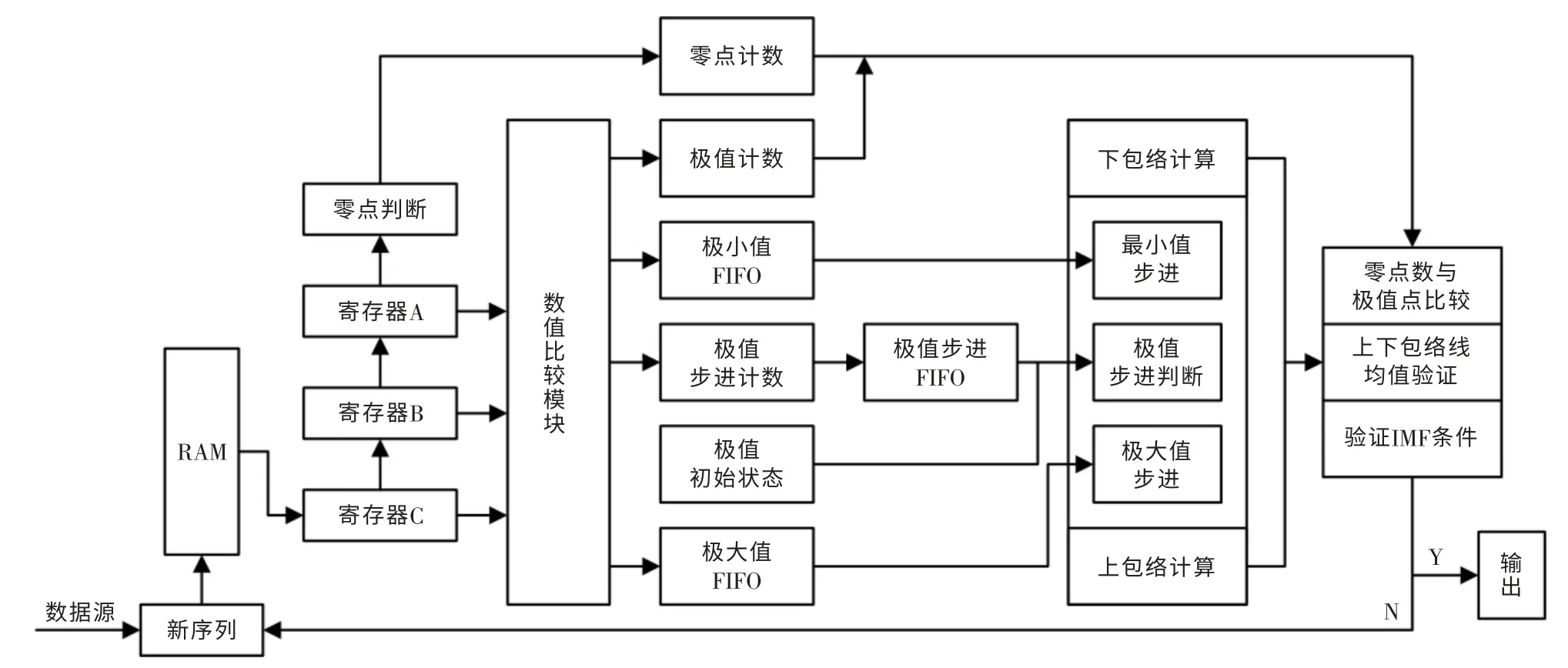
图2 EMD 信号FPGA 实现框图Fig.2 Block diagram of FPGA implementation of EMD signal
3 EMD 算法仿真验证
在此,利用FPGA 平台对高速列车行驶过程中车体前部横向加速度进行EMD 分解,以便于数据的后期分析,判断高速列车减震器的工作状态。
simpack 软件是一款用于机械/机电系统运动学/动力学仿真分析的多体动力学分析软件。利用该软件建立仿真模型,模拟高速列车运行过程中车体前部横向加速度。所用原始数据源于simpack 软件。
基于Xilinx FPGA 开发平台ISE 进行软件开发,并通过Modesim 仿真软件进行程序的仿真测试。Modesim 仿真结果的截图如图3所示。图中自上而下分别为IMF1—IMF8。分析仿真结果可知,随着IMF_cnt 由1 变为8,IMF 值变化频率逐渐变小,同时对比IMF_Y 的幅值可以清楚地判断出IMF4 和IMF5 的幅值最大,即信号能量最为集中。比对零点个数与极值点个数,符合EMD 分解原理。
4 结语
在微型化、高速化发展的大背景下,将EMD 方法移植到FPGA 平台,有利于分析检测设备小型化、通用化发展。同时,由于FPGA 器件的结构特点,通过并行化的处理方式能够提升EMD 算法的处理速度,可编程的特性能够增加系统开发的灵活性。将EMD 方法与希尔伯特变换结合,EMD 方法的应用领域将进一步扩大。

图3 IMF 仿真截图Fig.3 Screenshot of IMF simulation

