基于BP神经网络的极限传输容量预测方法
吴 锴,姚 方,王 生
(山西大学 电力与建筑学院,太原030024)
现代电力系统运行状态复杂多变,发生故障的风险增大,有效控制系统安全运行的难度增加。运行知识的发现是保证电网安全有效运行的必要手段[1]。传统离线模式下的关键断面选择和运行规则制定依赖于人类智能,难以满足智能安全分析的需求。随着人工智能技术的应用,结合电力系统实际运行数据、仿真计算数据[2-4],采用非线性模型分析电网运行状态,可以提高电网精细运行规则的制定效率,推动电网调控领域智能化发展。
传统的采用线性模型分析电网运行状态的方法很多,文献[5]提出一种适用于在线调度辅助决策的极限传输容量(total transfer capability,TTC)计算方法,考虑不同的发电负荷增长模式求出TTC 区间值,为后续研究精细规则提供了基础。文献[6-8]在分析离线规则弊端的基础上,解释了精细的电网运行规则,提高了运行知识发现的精确性能和实际应用性能。
如今,不少学者利用人工智能技术开展在电网调控领域的研究。文献[9]提出一种在改进向量机基础上的判断电网关键断面是否生效的方法,并采用层次聚类和K-means 聚类结合的技术分析断面运行知识,提高了训练效率。文献[10]从实际工程出发,采用智能网格法来计算暂态稳定约束下的TTC,但软件、硬件的需求较高,虽基本满足在线应用的要求,但计算过程复杂,成本高,实现难度大。总的来说,基于线性模型的TTC 计算过程复杂,经济性不高。因此,本文考虑采用人工神经网络训练的方法,运用机器学习相关技术,可以提高电网调度人员的工作效率,保障电网安全稳定供电,并且神经网络模型具有较强的可拓展性。
1 极限传输容量预测流程
基于BP 神经网络的电网关键断面TTC 预测流程如图1所示。主要分为基准运行数据获取、关键断面自动划分、仿真大数据模拟、特征属性选择、极限传输容量评估、人工神经网络训练6 个部分,具体功能描述如图1所示。
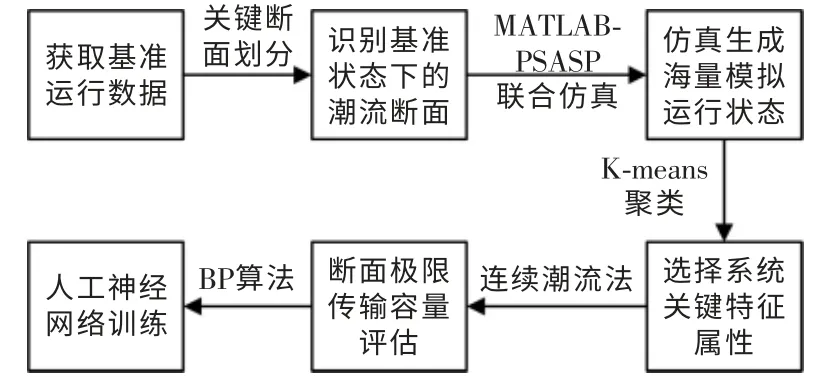
图1 基于BP 神经网络的断面TTC 预测流程Fig.1 Prediction process of TTC based on BP neural network
(1)运行数据获取
数据是进行自动学习的基础[11],运行数据主要考虑系统潮流量测数据,并将其作为获取仿真数据的基础,实际电网中主要从EMS 系统中获取实时运行数据,并忽略对系统运行影响较小的外部因素。
(2)关键断面划分
首先确定电网拓扑结构和潮流计算数据;然后,在电气分区的基础上,初步确立系统关键断面[12],在满足约束条件时选取潮流流向相同,传输功率偏高,安全裕度低的断面作为系统的关键断面。
(3)仿真大数据模拟
本文采用PSASP 和MATLAB 交互的方法生成仿真大数据[13-14]。实现MATLAB 控制PSASP 潮流计算模块,需构建MATLAB 与PSASP 交互接口,实现两者互联,并将仿真生成的数据库提供给后期神经网络训练使用。
(4)特征属性选择
特征选择是从大量初始特征中选择某些特征并要求所选特征包含描述整个系统的绝大部分信息。因此,特征选择是进行TTC 预测的关键步骤,合理的选取描述系统环境的属性与TTC 预测精度有着强相关性。
(5)TTC 评估
TTC 评估主要考虑断面划分、故障预设置、约束条件3 个关键要素。断面划分由前文提到的方法获取,约束条件主要包括静态安全、暂态稳定约束。静态约束条件主要考虑相关线路N-1 故障,暂态约束条件考虑线路发生首末两端三相短路故障。指定断面下的TTC 可表示为相关故障下断面所有联络线传输有功功率之和为最大值。
(6)人工神经网络训练
神经网络包含输入层,输出层,和一个或多个隐层[15],神经元作为连接各层的桥梁。神经元的权重和阈值的确立是实现神经网络的基础。本文中神经网络输入层向量为电力系统关键特征属性集合,输入层神经元数量由关键特征属性个数决定;输出层神经元仅有一个,表征系统关键断面的TTC 增量;隐层数量在重复训练中确定;各隐层神经元数量也具有不确定性,要根据实际训练效果确定。本文算例拟采用多层前馈神经网络训练机制,通过BP 算法反向求解。
2 关键细节
2.1 MATLAB 和PSASP 交互方法
电力系统分析软件PSASP 批量潮流计算时速度慢,基础数据修改麻烦,而MATLAB 可以弥补PSASP 计算能力上的缺陷。因此需要构建PSASPMATLAB 数据接口来实现PSASP 和MATLAB 混合仿真,接口结构如图2所示。
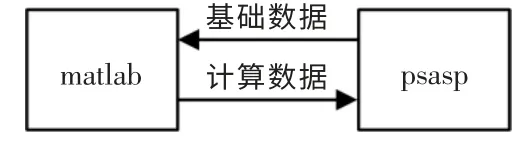
图2 PSASP-MATLAB 数据接口Fig.2 Data interface of PSASP-MATLAB
PSASP 提供的用户程序接口(UPI)是实现与MATLAB 混合仿真的前提。UPI 提供了程序编写的功能,同时MATLAB 可通过C 语言API 函数调用PSASP 的内部的潮流计算模块和暂稳计算模块进行仿真。PSASP 通过数据接口向MATLAB 提供计算基础数据,而MATLAB 计算完成后将数据信息更新至PSASP 软件中的mysql 数据库的指定位置。PSASPMATLAB 混合仿真实现了软件之间数据实时传输,提高了暂态仿真的批处理能力,其速度优于PSASP自带的批处理功能,可缩减仿真所耗费的时间。
2.2 仿真大数据模拟
选择系统某一典型运行状态作为获取仿真数据的基准潮流状态。影响系统潮流的因素包括网络拓扑结构、元件参数、不可控变量(系统负荷)、可控变量(节点电压、发电机有功出力等)。采用PSASPMATLAB 交互的方法生成海量仿真数据,在获取随机潮流状态时,保持系统拓扑结构、元件参数不变。小范围内改变可控变量如节点电压水平,调整发调机的有功出力,改变系统负荷,各节点负荷按等比例分配。而系统总发电量PG和系统总负荷PL总量基本相当,差额负荷通过平衡节点补充。最后计算各仿真运行方式下的潮流数据,在所得数据的基础上,分别计算所有的仿真断面对应的TTC。并统计特征属性包括系统总发电出力、各分区发电出力、负荷有功、发电厂的有功出力、各母线电压水平等与基准潮流对应值的偏差量,和目标属性即仿真潮流下断面TTC 与基准潮流下断面TTC 的偏差量。
2.3 特征属性选择
本文采用基于K-means 聚类的分组特征选择方法[16]。由于电网特征属性数量多而杂,避免聚类过程中出现偏差,首先将初始特征集合F 按照有功功率、电压等分组处理;然后根据具体要求完成各个组的特征属性选择;最后将各组所选特征组成整个系统的关键特征集合,获得最终的关键特征属性集合如式(1)所示:

式中:m 为所有特征属性的分组数量。
针对单一分组内关键特征属性选择,通过定义评价准则确定。首先,对于待选特征Xi和目标特征集合Y,定义关联程度系数Ri,Ri如式(2)所示:

由式(2)可知,Ri的大小反映了特征Xi和目标特征集合Y 的关联程度,其值越大,表示两者关联程度越大。然后,定义待选特征Xi和Xj之间的关联程度系数Rij,Rij如式(3)所示:

由式(3)可知,Rij的大小反映了特征Xi和Xj的关联程度,其值越小,表示两者冗余度越小。因此,在选择的过程中优先选择关联程度大但冗余度小的特征组成关键特征集合。
2.4 极限传输容量评估方法
单一断面TTC 目标函数表示为断面所有联络线路输出功率之和为最大值,如式(4)所示:
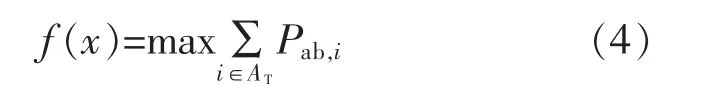
式中:AT为断面的联络线路集合;Pab为断面第i 条联络线路的有功潮流量;x 为TTC 预测问题中的决策向量。
针对多断面系统,单独计算满足某一断面的TTC值是不严谨的。因此,要考虑同时满足系统中所有断面TTC,对所有区域进行协调同步预测,经济分配和优化利用电力网络资源。故采用多目标优化对多断面系统进行TTC 预测。目标函数如式(5)所示:

式中:n 为参与TTC 预测的系统关键断面数目。
静态安全条件下考虑常规的电压幅值极限约束和功率极限约束,暂态稳定约束条件下考虑发电机功角约束。功角约束如式(6)所示:

式中:t∈[0,T];T为所研究的动态过程时间段(取5 s);δmax为故障状态下任意2 台发电机动态稳定允许的功角差上限(取180°);δi(t)、δj(t)为t 时刻故障时系统中任意2 台发电机i、j 的功角;G 为系统发电机集合。
2.5 基于BP 神经网络的TTC 预测训练
神经网络在信号前向传递过程中,输入层信号经过各隐层逐级传播直至输出层,下一层神经元受到上层神经元状态影响。训练过程中输出层结果与期望值误差较大时,则进入反向求解过程。重新调整参数权重和阈值,使得最终训练结果符合预期目标。神经元传播如式(7)所示:

式中:Wi,j为相邻层i 与j 之间的权重;Xi为神经网络中第i 层神经元;Bi为偏置量。BP 神经网络求解过程可由前向传播和权重迭代构成,误差值在前向传播过程中产生,表示实际值和期望值的差值。权重系数随着训练过程不断迭代,在权重迭代环节,将误差值对上一次训练权重的一阶导数作为迭代权重系数。迭代权重系数如式(8)所示:
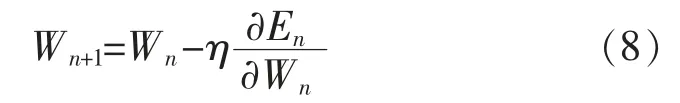
式中:Wn为第n 次迭代前的权重系数;η 为学习速率;En为第n 次迭代前的响应误差。
根据特征选择的数量确定输入层神经元的个数;输出层数量唯一,表征目标属性TTC 的增量;隐层层数以及各隐层神经元数量需要经过重复训练确定。利用BP 神经网络训练完成后得到关键特征属性和TTC 增量的非线性关系,如式(9)所示:

式中:ΔPTTC为仿真样本中各个关键断面的TTC 与基准状态下各个关键断面的TTC 的增量。
针对TTC 预测的BP 神经网络结构如图3所示。

图3 BP 神经网络结构图Fig.3 Structure diagram of BP neural network
3 仿真算例分析
为有效分析多断面系统下的TTC 评估,使用PSASP 搭建7 机36 节点系统模型,具体结构如图4所示,在此模型基础上进行基于BP 神经网络的TTC 预测方法验证。
首先将节点系统分区处理,便于理解断面选择。根据模拟潮流状态下的计算结果分析,该系统可以划分出3 个分区,分别标记为A、B、C,简化后系统分区如图5所示。同时分区A 与分区B、C 之间的联络线可以标记为关键断面一;分区C 与分区A、B 之间可以标记为关键断面二。

图4 7 机36 节点系统拓扑结构示意图Fig.4 Topological structure of 7-machine 36-node system

图5 7 机36 节点系统简化分区示意图Fig.5 Simplified partition diagram of 7-machine 36-node system
以关键断面一为例进行海量状态仿真,可以模拟系统不同时期运行状态。首先,分区A 作为发电区域,分区B、C 作为受电区域,然后,在某一基准潮流状态基础上通过微调发电区A 内发电机的有功出力或者微调机端电压,受电分区B、C 内微调负荷增长模式,各负荷节点可按比例增加或者减少,保持系统总发电量PG和总负荷量PL基本一致,不足部分由平衡节点补充,分别统计系统总发电出力,分区A、B、C 发电出力,系统中各发电机有功出力,负荷有功以及各母线电压水平作为仿真数据库基本组成。生成2500 份仿真样本,其中2000 份样本作为训练集,500 份样本用于测试集。最后采用基于K-means 聚类的分组特征选择方法进行降维处理,从样本原始输入属性中选择与目标属性相关性较强的属性作为关键特征,目标属性用ΔPTTC表示。样本原始输入属性为仿真样本中各个电网运行参数与基准状态下各个电网运行参数的增量。表1 仅列出仿真样本中部分统计数据,并以标幺值的增量形式记录。
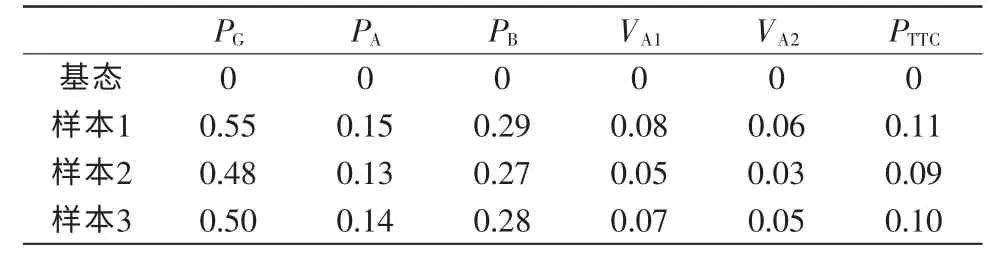
表1 仿真样本部分统计数据Tab.1 Some statistical data of simulation samples
表中:PG为系统中所有发电机有功出力;PA、PB分别为分区A、B 内发电机有功出力;VA1、VA2分别为节点A1、A2 侧电压;PTTC为断面传输有功功率。
经过降维处理后选择出3 个关键特征属性,分别记为VA2、VA3、VBC2,它们是影响关键断面一的TTC预测的关键特征属性,并将选择出的3 个特征属性作为BP 神经网络训练的输入层神经元,除特征属性外,再加上偏置量神经元共同组成输入层;输出层神经元仅为1 个,表示目标属性TTC 的增量;隐层一共有4 层,各隐层神经元个数分别为8、5、10、5,学习率设为0.8。经过训练后得到的TTC 预测模型如式(10)所示:
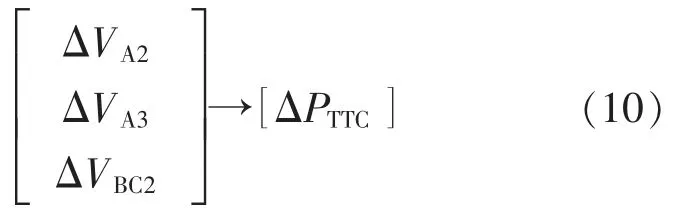
分析结果可知:①BP 神经网络训练平均时间约为10 s,平均预测准确率可达98.8%,训练时间略高于传统线性化模型,但也能保障电网安全运行的实时性要求。②由于BP 算法考虑了电力系统非线性的特点,该模型预测准确率相对于线性模型更高。如将非线性模型应用于实际电网,可有效提升电网调度人员的决策能力,保障电网安全有效运行。随着科学计算能力的提高,非线性模型预测时间较慢的瓶颈也将会有所突破。
4 结语
本文提出了基于BP 神经网络预测断面TTC 的实验方法,经过重复训练得出电网关键特征属性和TTC 增量间的非线性关系,可以有效提高电网调度人员工作效率,保障电网安全稳定运行及可靠供电。同时,运用机器学习相关技术,具有较强的可拓展性。

