基于激光雷达的叉车型自动导引小车定位研究

钱东海，陈 成，孙林林，赵 伟，刘 洋

（上海大学 机电工程与自动化学院，上海200444）

随着科学技术的不断发展与提高，机器人在许多领域都开始被广泛使用，移动机器人的定位是作为执行任务的最基本要求。即时定位与建图（simultaneous localization and mapping，SLAM）问题可以描述为机器人在未知环境中从一个未知位置开始移动，在移动过程中根据位置估计和地图进行自身定位，同时在自身定位的基础上建造增量式地图，实现机器人的自主定位和导航，可以使用激光雷达或者相机等传感器实现。激光雷达具备便利、快速以及准确等优势被广泛的作为定位传感器使用。目前激光SLAM 主要基于图优化的方法进行求解，激光SLAM 主要分为前端和后端两个部分，前端扫描匹配主要是针对帧与帧之间的激光点云数据进行处理，求解两帧相对位姿；后端则利用到扫描匹配来进行回环检测，在检测到回环时则进行全局的图优化，提高AGV 在整个路径中的定位精度。

1 扫描匹配

“扫描匹配” 这一概念主要出现在机器人学相关文献中，主要通过将激光扫描点云配准到同一坐标系下而得到相对位姿变化[1]。激光扫描匹配处理的是移动载体运动时雷达的扫描数据，点云较稀疏，且误差和噪声均较大，大多要求实时处理，力求在精度和效率之间寻求平衡。目前前端扫描匹配的方法主要分为3 类：①基于点的扫描匹配；②基于特征的扫描匹配；③基于数学特性的扫描匹配。基于点的扫描匹配是目前主流的方法，主要有以下几种方法。基于最近点迭代算法[2]（interactive closest points，ICP）进行逐点匹配，其缺点是需要在每次的迭代中进行大量的点对应搜索；极坐标扫描匹配[3]（polar scan matching，PSM）利用激光扫描的自然极坐标来估计它们之间的匹配，避免了对应搜索。但是扫描必须经过预处理才能在极性扫描匹配器中使用；实时相关扫描匹配[4]方法采用穷举抽样的方法进行扫描匹配，通过设计的几个优化，该方法能够实时应用；基于正态分布变换[5]（normal distribution transform，NDT）的扫描匹配，该方法将单次扫描中的离散2D 点变换为定义在2D 平面上的分段连续且可微的概率密度，概率密度由一组容易计算的正态分布构成，另一帧扫描与NDT 的匹配就定义为最大化其扫描点配准后在此密度上的得分，并进行优化求解；基于优化的扫描匹配[6]，通过障碍物概率的方式构建误差函数使用优化方法对最佳位姿进行求解，其主要采用的是高斯牛顿法。本文主要研究基于点的扫描匹配。在基于优化的扫描匹配的基础上，对地图插值时使用双三次插值，能够获取更优的插值精度，优化方法使用列文伯格-马夸尔特法，能有效避免高斯牛顿法的缺陷。

2 叉车型AGV 激光雷达定位中的位姿变换

本文是以叉车型AGV 为研究对象，在AGV 上安装激光雷达实现导航定位。激光雷达传出的点云数据需要进行处理后才可以使用，同时为了实现AGV 的定位要给出激光雷达与其的位姿变换关系。主要包含3 个坐标系： 全局地图坐标系、AGV 坐标系、激光雷达坐标系。

2.1 AGV 运动学模型

本文激光雷达主要是安装在叉车型自动导引小车上，该叉车型AGV 为单舵轮驱动，通过控制舵轮实现AGV 的转向功能以及驱动功能。AGV 主要的运动学模型如图1所示。

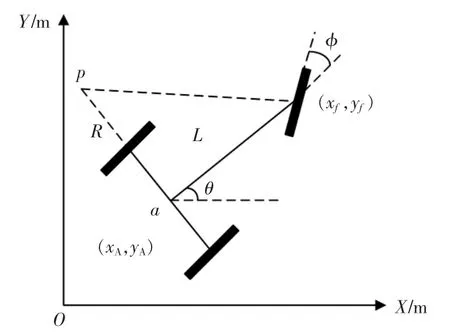
图1 AGV 运动学模型Fig.1 AGV kinematics model

选取图中从动轮的中心点a（xA，yA）为AGV 位姿的参考点，即AGV 在全局地图坐标系下的位置；（xf，yf）为舵轮在全局地图坐标系下坐标；L 为车体轴距；θ 为车体方位角；φ 为舵轮转向角；V 为舵轮运行线速度；R 为车体最小转弯半径。

由图可知AGV 角速度与线速度之间的关系，同时也可以得出AGV 舵轮中心点与从动轮中心点之间的位置关系。当AGV 从k 时刻运行到k+1 时刻，AGV 在全局地图坐标系下的坐标如下：

式中：xk′，yk′为AGV 在k 时刻时舵轮在全局坐标中的位置；φk，φk+1分别为AGV 在k，k+1 时刻的舵轮角度；xk+1，yk+1为k+1 时刻AGV 在全局坐标系下的位置；θk，θk+1分别为AGV 在k，k+1 时刻的车体角度；t 为两点之间的运动时间；ω 为舵轮角速度。

由于激光雷达是安装在AGV 上，因此通过激光雷达实现AGV 的定位时，需要用到激光雷达与AGV车体之间的相对位姿，该值通过测量即可得到。为便于描述，将上述AGV 在全局地图坐标系下k+1时刻的车体位姿表示，以表示激光雷达在全局地图坐标系下的位姿。为了计算激光雷达在全局坐标系下的位姿，需要先将激光雷达变换到AGV 坐标系下，在从AGV 坐标系变换到全局坐标系下，则其关系如下：

在AGV 运行过程中，根据舵轮在k 时刻角速度ω、转角φk以及车体的方位角θk，可以推算出AGV在k+1 时刻的位姿，利用激光雷达与AGV 车体之间的相对位姿变换矩阵，可计算出激光雷达的位姿，在点云匹配中可将该位姿作为激光雷达初始位姿进行迭代优化。

2.2 激光雷达测量数据

对于二维激光雷达通常采用三角测距原理或者飞行时间进行测距，每次测距时，激光雷达通过发射器发射红外激光信号，激光信号射到障碍物体后产生的反射光被接收器接收，然后经过内部处理器计算得到障碍物体到激光雷达的距离以及当前夹角。在电机的驱动下，实现360°测距，获得点云数据，包括角度θ=｛θi=（i-1）×360/n，i=1…n｝；距离d=｛di，i=1，…，n｝，其中n 为激光雷达每一圈扫描点个数；θi与di分别为第i 个扫描点的角度与距离。

对于激光雷达点云数据中第i 个扫描点，在激光雷达坐标系下，则有：

式中：（xi，yi）和（di，θi）分表示第i 个扫描点在激光雷达笛卡尔坐标系和极坐标系下的坐标值。激光点云数据（xi，yi）在全局地图坐标系下的坐标转换关系通过下式计算得到：

式中：（xi，yi）为第i 个数据点在激光雷达坐标系下的坐标值；（xi′，yi′）为第i 个数据点在全局地图坐标系下的坐标值，激光雷达位姿如式（8）所示。

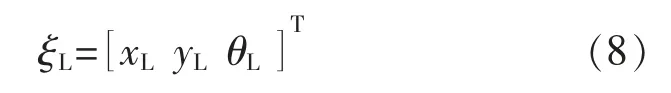
式中：xL，yL表示激光雷达在全局地图坐标系下的坐标值；θL表示激光雷达在全局地图坐标系下航向角。

3 栅格地图创建及栅格障碍物概率求取

本文进行点云匹配的策略是利用激光雷达在初始位姿处的激光点云构造栅格地图，并且在AGV运动过程中采集新的激光点云数据不断地更新栅格地图。栅格地图的创建与基于栅格地图的AGV导航是同步进行的。本文所要解决的是已知前后两帧激光点云数据，求得后一帧点云数据AGV 所在位姿相对于前一帧点云数据AGV 所在位姿的位姿变换。

地图的构建方法有很多种，通常会根据实际情况以及需要来决定使用何种类型的地图，本文选择使用栅格地图来作为扫描匹配的参照。栅格地图是将二维地图用一系列的网格单元来表示[7]，对于其中的每个网格，用“0”和“1”分别表示无障碍物和有障碍物两种状态。

上述栅格地图是离散分布，这在一定程度上限制了可达到的精度，本文使用栅格障碍物概率对栅格中各点是否存在障碍物进行描述，它是栅格中各点位置的连续函数，并且扫描匹配时需要求其偏导数。为使得障碍物概率函数连续且可导，本文选择双三次插值来求取每一个栅格的障碍物概率函数。

双三次插值是对插值点周边最近的16 个采样点进行加权平均。假设插值点位于Q0（x，y），其中x，y 为任一小数；i，j 表示其整数部分；u，v 表示其小数部分。该方法选取以点（i-1，j-1）到（i+2，j+2）构成的包含16 个采样点数据的矩形网格。

本文使用ROBERT G.KEYS[8]提出的基于BiCubic 基函数的双三次插值法，将其用于创建激光点云栅格地图中各栅格的障碍物概率，该方法利用三次多项式求取原函数的最佳逼近函数，BiCubic 基函数形式如下：

式中：a 取-0.5。当a=-0.5 时能产生相对于原始函数的采样间隔的三阶收敛；若a 为其他值时只能产生相对于原始函数的一阶收敛。

在激光点云栅格地图中，对于一给定的栅格，求取其栅格障碍物概率，需用到其邻近的16 个栅格，x 方向分别以i-1，i，i+1，i+2；y 方向分别以j-1，j，j+1，j+2 为下标表示16 个邻近的栅格。令函数f表示点对应位置的栅格障碍物概率，可以分别计算出函数f（Q0）和的值通过式（10）与式（11），式（12）。

其中A，B，C 分别为

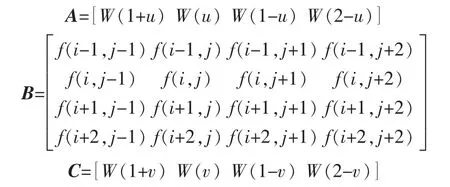
分别求X，Y 轴方向的偏导：

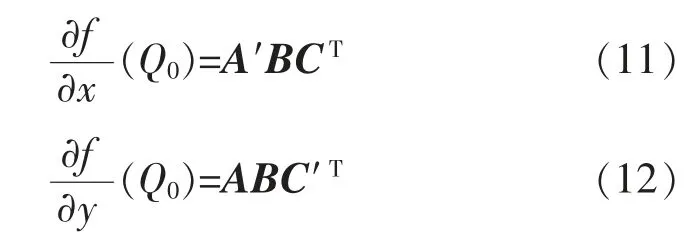
式中：A′，C′分别为

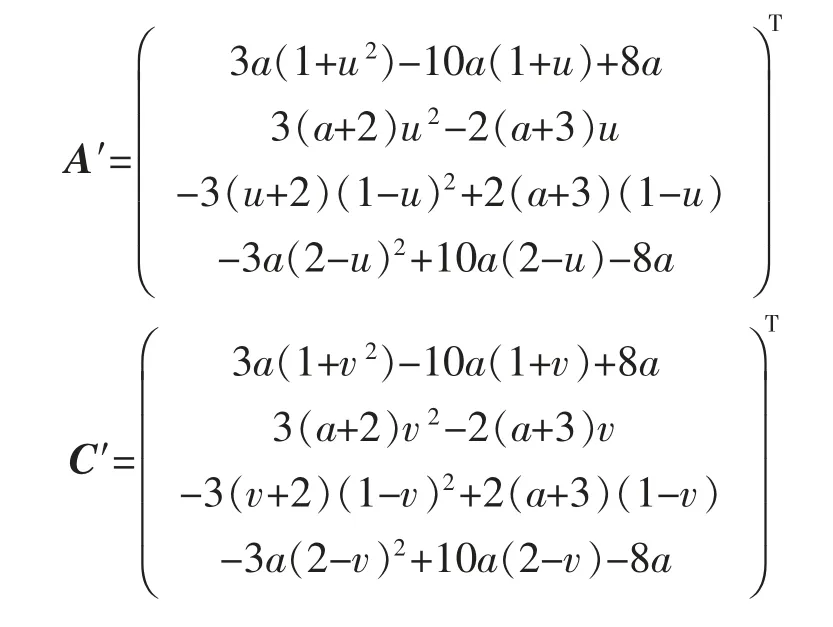
4 激光点云匹配的优化求解

激光点云匹配是将两帧激光点云彼此对齐，本文以前一帧激光点云数据构造一个栅格地图，然后根据式（5）求取第二帧激光点云所在时刻的理论位姿，并作为第二帧精确位姿迭代求解的初始位姿。

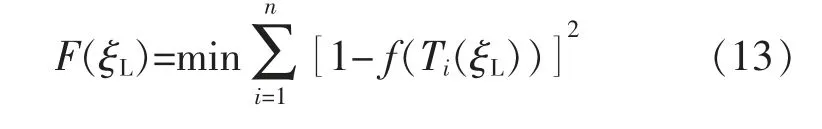
式中：函数Ti（ξL）表示将激光雷达坐标系下的点转换到全局地图坐标系下。

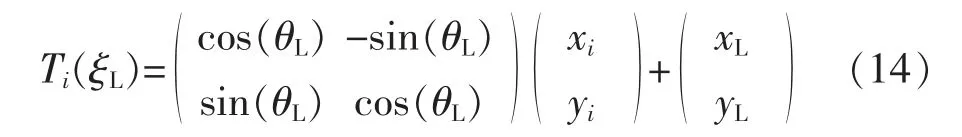
式（13）为一个非线性最小二乘问题，可将其转换成一系列的线性最小二乘问题，通过迭代计算来求解[9]。最常用的算法为高斯牛顿法[10]，该方法用JTJ 作为牛顿法中二阶Hessian 矩阵的近似，从而省略了计算Hessian 矩阵的过程。高斯牛顿法原则上要求近似Hessian 的矩阵JTJ 是可逆的，但实际中可能为奇异矩阵或者病态的，导致算法不收敛。列文伯格-马夸尔特算法可以避免高斯牛顿法出现的病态与非奇异问题，提供更加稳定的增量，该算法主要是在高斯牛顿法的基础上加上信赖区域以改进其问题。本文选择列文伯格-马夸尔特算法进行优化求解。

从AGV 运动学方程可以获得位姿估计的初始值，然后通过优化目标方程去估计增量。

对上式进行一阶泰勒线性展开[5]，并将展开后的方程对ΔξL求导并令其等于0，可得到下式：

式中：H，J 为

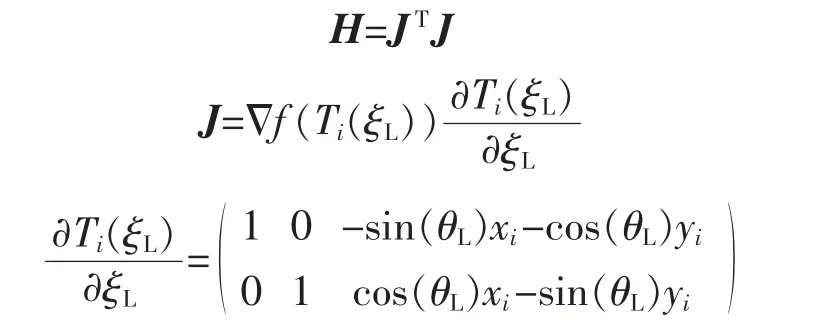
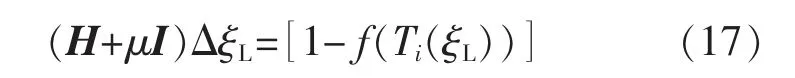
式中：I 为单位矩阵；μ 为一个正实数。当μ=0 时，该算法退化为高斯牛顿法；当μ 很大时，该算法退化成了最速下降法。μ 的值会根据优化进行的状态随时调整，这个参数即控制着优化前进的方向与步长。主要通过下述策略来对μ 值大小进行调整，需要引入2 个额外的参数：ρ，ν，其中ρ 由下式计算得出；ν的初始值给定为2。

其中ψ 为：

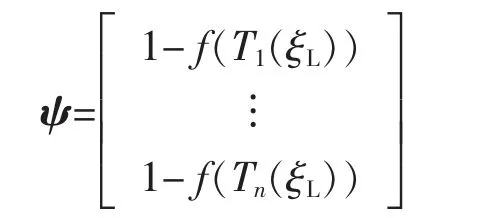
在每轮迭代过程中ρ 代表每次前进近似函数的变化量与F（ξL）变化量的差异。如果ρ>0，就意味着此次迭代前进的方向是正确的，继续进行下一轮迭代；反之，则迭代前进的方向不对，就需要利用另外一个参数υ 来调整，调整的策略是μ＝μ×ν。持续此迭代过程直至满足终止条件，即可获得前后两帧的相对位姿。

5 实验与分析

为验证本文所提出方法的准确性，需要通过激光雷达采集真实的数据进行实验。由于AGV 主要的运行环境为室内场景，因此选用2D 激光雷达。本文采用德国SICK 公司的NAV350 激光雷达为室内型2D 激光雷达传感器，包括反光板模式和环境轮廓检测模式，在环境轮廓检测模式下，能够输出周围轮廓的点云信息。该雷达测量距离为70 m，每帧数据有1440 个点。激光雷达安装在AGV 上进行工作，并且为了获得准确数据，在墙上安装反光板，该型号激光雷达可根据反光板计算出真实位姿，实验设备如图2所示。

图2 叉车型AGV 实物图Fig.2 Physical picture of forklift AGV

在反光板模式下，激光雷达可通过对反光板测量计算得到位姿，因此以反光板计算得到的位姿作为基准，分析本文算法求解位姿的误差。图3 给出了相邻两帧激光点云数据图，本文算法主要就是在环境轮廓检测模式下，根据两帧点云数据计算出两帧之间的相对位姿。

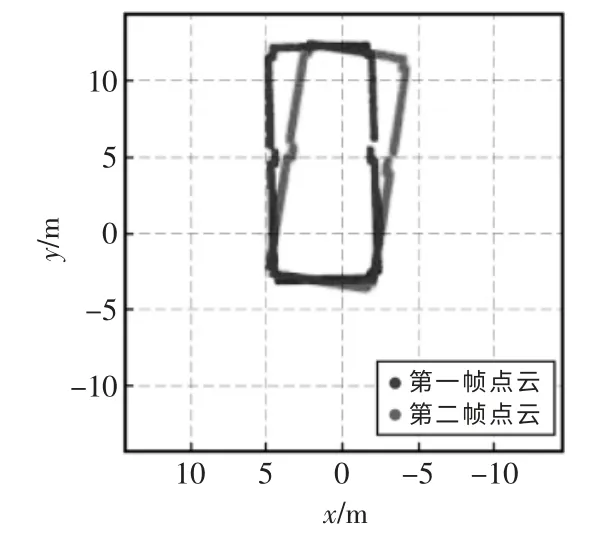
图3 相邻两帧激光点云分布图Fig.3 Distribution of laser point cloud of two adjacent frames

在反光板模式下，测出的位置为x=0.3432 m；y=0.2034 m；角度的弧度值为0.1854。使用本文算法计算出两帧之间的相对位姿为x=0.3435 m，y=0.2161 m；角度的弧度值为0.1841。因此在x 轴方向的误差为0.0003 m；y 轴方向上的误差为0.013 m，角度弧度值的误差为0.0013。通过上述实验验证了本文算法的有效性与稳定性。

6 结语

本文以叉车型AGV 为研究对象，基于激光雷达研究前后两帧激光点云匹配问题，从而求解两帧点云所对应的AGV 位姿变换关系，最终应用于AGV的定位与导航。算法对前后两帧激光点云数据进行处理，利用第一帧点云数据构造出一个栅格地图，使第二帧点云数据与前一帧构造的栅格地图对齐，以此来构建误差方程，并采用非线性最小二乘法求解误差函数的最小值，从而求得前后两帧的相对位姿。实验结果表明该算法能有效地计算出相邻两帧点云数据的相对位姿，因此解决了SLAM 前端点云匹配计算位姿的问题，同时SLAM 后端也可利用到点云匹配来进行回环检测，在检测到回环时则进行全局的图优化，提高AGV 在整个路径中的定位精度。