基于MVO算法针对风电SSCI抑制的参数智能优化
王 翔,苏玉香,沈晓群
(1.浙江海洋大学 海洋工程装备学院,舟山316022;2.西南交通大学 电气工程学院,成都611756)
风电作为新能源的代表在近年来发展迅猛。采用串补输电线路以提高远距离送电能力,是消纳风电的有效措施[1]。然而,风电机组控制器与固定串补之间的相互作用,极易引发次同步控制相互作用(SSCI),此种类型的次同步振荡有别于传统的机械轴系参与的振荡类型(SSR、SSTI),其振荡发散速度更快,危害更大[2]。美国德克萨斯州[3]和我国河北沽源[1,4]的风场发生的次同步振荡都是典型的SSCI 类型。随着电力系统的逐渐电力电子化,多变流器与电网之间的动态相互作用所导致的新型次同步振荡(SSCI)问题已成为研究热点[5]。
现有的抑制风电次同步振荡的方法可以分为两类:一类是增设FACTS 装置,如:静止同步补偿器、可控串补(TCSC)等,增设FACTS 装置的显著缺点是高昂的设备和维护成本;另一类是配置附加阻尼控制器(supplementary damping control,SDC),或优化控制参数,以增加系统软件阻尼。文献[6]基于特征值分析设计了一种直接作用于转子侧(RSC)电压的附加阻尼控制器(SDC),有效抑制了SSCI,但附加阻尼控制器及其参数的设计十分复杂。
大量研究表明,双馈风机SSCI 与风机变流器的控制参数有关[7-11],但没有给出具体参数的整定方法。近年来,基于智能算法优化风机控制参数已有不少研究[12-13],却很少有以抑制双馈风电场SSCI 为目标的变流器参数优化研究。
文献[14]基于单纯形算法(Simplex)优化了可控串联补偿装置(TCSC)参数,提高了对次同步振荡的抑制效果,但其并没有对机组本身的控制参数进行优化,忽略了机组自身抑制振荡的潜力。文献[15]采用特征值分析法,得出SSCI 主要与变流器的控制和发电机转速有关,并基于NSGA-III 算法,以最大化振荡模态阻尼比为目标函数,优化了变流器参数,有效抑制了系统振荡;但该方法以特征值分析法为基础,其系统各动态元件参数化模型很难精确建立,且求解高阶特征值矩阵会面临“维数灾”问题。
本文将抑制DFIG 次同步控制相互作用(SSCI)问题转化为PI 参数整定问题。以Simulink 时域仿真程序计算结果作为目标函数,基于多元宇宙优化算法(MVO)智能寻找最优参数组合,达到抑制SSCI的目的。然后与现有的配置附加阻尼控制器(SDC)和增设TCSC 装置的抑制方法对比,结果表明本文方法能够更加有效可靠地抑制SSCI。最后,将MVO算法与PSO-GSA、GWO 算法对比,体现了MVO 算法在多参数组合寻优问题上的优越性。
1 多元宇宙优化算法
多元宇宙优化算法(MVO)[16]基于多元宇宙理论中的黑洞、白洞、虫洞概念。每个宇宙都有膨胀率,膨胀率低易产生黑洞,反之易产生白洞。在MVO 算法中存在2 种物质交换机制: 一是白洞发出物体,黑洞接收;二是虫洞随机让物体在宇宙中(或跨宇宙)旅行。
类比于其他群体智能算法,在MVO 算法中,多元宇宙群体即是种群,其数学模型可用式(1)表示:

式中:n 表示宇宙(候选解)的数量;d 表示每个宇宙中物体(变量)的数量。
MVO 算法为每个宇宙分配一个膨胀率,该膨胀率与每个解的目标函数值成比例;采用轮盘赌机制,模拟黑洞-白洞间的物体交换。该机制保证了MVO 算法在解空间搜索的高效性。先根据膨胀率对宇宙排序,再通过轮盘赌机制选择物体作为白洞传送对象。其数学模型如式(2)所示:

式中:NI(Ui)表示第i 个宇宙的归一化膨胀率;r1是[0,1]范围内的随机数;表示经轮盘赌机制选择的第k 个宇宙的第j 个物体。
为了提高MVO 算法的开发性,模拟了虫洞可随机将各宇宙中的物体传送到当前最佳宇宙,而不考虑膨胀率大小的特性,其数学模型如式(3)、式(4)所示:
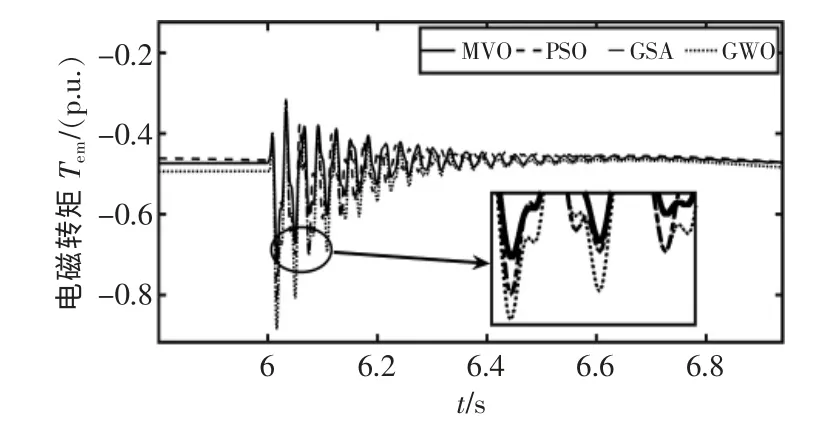
当r2 当r2≥WEP 时: 式中:Xj表示到目前为止形成的最佳宇宙的第j 个参数;ubj和lbj表示该变量的上、下界;表示第i 个宇宙的第j 个参数;r2,r3,r4是[0,1]中的随机数。 虫洞存在率WEP 越大,则解空间中元素随机交换概率越大,体现算法的开发性能;旅行距离率TDR 表示物体通过虫洞向最优宇宙移动的步长,体现算法的局部搜索能力。两个参数的自适应公式为 式中:l 为当前迭代次数;L 为最大迭代次数。本文取min=0.2,max=1,p=0.6。 根据上文对MVO 算法概念模型和数学模型的解释,MVO 算法与Simulink 时域仿真程序相结合的非线性优化方法流程如图1所示。 (1)定义重要参数值WEPmin、WEPmax、p、L,初始化多元宇宙种群; (2)在Simulink 中搭建详细的双馈风电场仿真模型,定义待优化的系统控制参数为d 维参数空间[x1,x2,…,xd],并设置取值范围[lb,ub]; (3)给Simulink 仿真参数赋值,由仿真结果计算各宇宙个体适应度值F(Ui),筛选出当前最优宇宙; (4)根据膨胀率对各宇宙个体排序,根据式(2)模拟黑洞-白洞隧道,执行轮盘赌机制; (5)根据式(3)、式(4)模拟虫洞隧道,更新宇宙种群,根据式(5)、式(6)更新WEP、TDR; (6)若达到最大迭代次数,则停止迭代,输出最优宇宙U′;否则重复(3)、(4)、(5)过程,直到满足终止判据。 图1 MVO 算法优化流程Fig.1 MVO algorithm optimization flow chart 本文采用单机等值模型来表示整个100 MW(66×1.5 MW)的双馈型风电场,在Matlab/Simulink中搭建如图2所示的双馈风机单机系统模型。图2中T 为升压变压器,RL、XL为输电线路的等值电阻和电感,XC为串补电容。 图2 双馈风力发电机模型框图Fig.2 Block diagram of doubly-fed wind turbine model 当系统发生由L-C 构成的电气自激振荡(IGE)时,这种振荡会因变流器的控制引入的负阻效应在滑差频率下大幅增强[17],导致SSCI。双馈风机转子侧(RSC)、定子侧(GSC)变流器控制结构如图3所示。 图3 DFIG 变流器控制框图Fig.3 Control block diagram of DFIG converter 文献[15]基于特征值分析法得出:双馈风机SSCI的振荡模式对Vdc和ωr高度敏感,主要受变流器的控制和发电机转速影响。为了减少参数维度,将d、q轴控制参数合并为一组,无功外环采用电压管理器(Voltage regular)取代PI 控制器;最后确定待优化的PI 参数为Kp1~4,Ki1~4。 为了直观有效地判断本文方法对双馈风机SSCI 的抑制效果,以电磁转矩瞬时值Tem(t)与稳态值Tem0的偏差的绝对值在[t1,t2]内的积分作为目标函数[14],如式(6)所示: 利用Matlab/Simulink 建立了图2所示的双馈风电系统模型,以验证MVO 算法与Simulink 时域仿真程序相结合的非线性优化方法的有效性。 当风速过低、系统固定串补较高,或因线路故障导致系统拓扑结构发生变化引起串补度突然升高等,都有可能引发SSCI。图4 显示了风速10 m/s时,系统线路固定串补度由0~6 s 的15%上升到6~10 s 的36%后,双馈风电机组有功功率P、无功功率Q、电磁转矩Tem发生的等幅振荡现象,并与MVO 算法优化变流器控制参数后的仿真波形对比,优化前后,变流器控制参数如表1所示。仿真结果表明,MVO算法智能优化后的变流器参数组合能够有效抑制双馈风机的SSCI,验证了本文所提方法的有效性。 图4 DFIG 系统在优化前与MVO 算法优化后的仿真图(风速10 m/s)Fig.4 Simulation diagram of DFIG system before optimization and MVO algorithm optimization(wind speed 10 m/s) 表1 优化前、MVO 优化后PI 参数对比Tab.1 Comparison of PI parameters before optimization and after MVO optimization 在仿真参数及串补度突变条件不变的情况下,在原仿真模型中分别加入了附加阻尼控制器(SDC)和TCSC 装置来抑制SSCI,三种方法的仿真结果与抑制效果对比如图5所示。仿真结果表明本文方法对DFIG 的SSCI 抑制效果的显著性。 图5 三种方法对双馈风机SSCI 抑制效果仿真图(风速10m/s)Fig.5 Simulation diagram of SSCI suppression effect of different methods on DFIG(wind speed 10 m/s) 从图5 的仿真结果可以看出,MVO 算法优化后的DFIG 系统,相比于配置附加阻尼控制器(SDC),显著降低了振荡幅值。从图5(a)有功功率的仿真结果可以看出,本文方法与增设TCSC 装置相比,抑制效果相当;但从图5(b)无功功率控制和图5(c)电磁转矩的振荡抑制上来看,本文方法更加可靠有效。 为了体现MVO 算法的优越性,使用了PSO-GSA、GWO 两种目前主流的算法与之对比,三种算法优化后的变流器控制参数组合对SSCI 的抑制表现如图6所示。显然,MVO 算法优化后的电磁转矩Tem的振荡幅值较其他两种算法优化的结果要更低。不同算法迭代过程如图7所示,MVO 算法较另外两种算法而言,其全局寻优能力更好。 图6 MVO、PSO-GSA、GWO 算法优化后的电磁转矩仿真图(风速10 m/s)Fig.6 Electromagnetic torque simulation diagram after optimization of MVO,PSO-GSA and GWO algorithms(wind speed 10 m/s) 图7 不同算法迭代寻优对比曲线Fig.7 Comparison curve of iterative optimization of different algorithms 本文将双馈风机次同步相互作用(SSCI)抑制问题,转化为控制参数整定问题,并将多元宇宙优化算法(MVO)与Simulink 仿真程序相结合的非线性参数优化方法引入到变流器的参数优化中。以最小化电磁转矩振荡为目标,对双馈风机变流器控制参数进行整定,能够有效抑制双馈风机的SSCI。在双馈风机SSCI 抑制的参数整定问题上,MVO 算法与现有的PSO-GSA、GWO 算法相比,能更快速的寻找到最优参数组合,且不易陷入局部最优。与现有的配置附加阻尼控制器(SDC)和增设TCSC 装置方法相比,基于MVO 算法优化变流器控制参数的方法对DFIG 的SSCI 有更好的抑制效果。


2 MVO 与Simulink 结合的优化方法

3 针对SSCI 抑制的参数优化算例
3.1 待优化风电场模型


3.2 待优化参数
3.3 目标函数
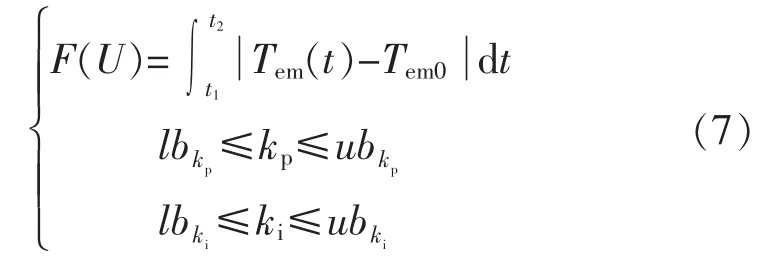
4 仿真验证与分析


4.1 与SDC 和TCSC 抑制效果对比

4.2 不同算法的比较

5 结语

