在初中数学教学中渗透与应用建模思想

陆颖

[摘 要]建模思想是初中数学的重要思想之一，它对学生体会与理解数学与其他事物之间的联系起着重要的作用.着重探究建模思想在初中数学教学中的渗透与应用，为提升初中数学教学的质量与效率提供良好条件.

[关键词]建模思想;初中数学;应用;渗透

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）05-0033-02

建模思想是初中数学的重要思想之一，它对学生体会与理解数学和其他事物之间的联系起着重要的作用，有助于学生解决各类数学问题.

一、初中数学教学渗透与应用建模思想的意义

数学课程标准明确指出，要注重发展学生的建模思想.建模思想的作用十分显著，可为学生解决问题提供条件与基础，帮助学生树立数学与生活紧密相关的意识，不断增强学生的数学实践应用能力.同时，在教师传授建模思想的过程中，还能激发学生学习数学的兴趣和好奇心，提高学生学习的自信心.在初中数学教学中渗透与应用建模思想很有意义.

二、初中数学建模的一般步骤

教师指导学生建模时，可按照如下步骤进行：

（1）认真审题，分析题意为建模做准备.

（2）从问题中简化情境，假设数学模型.

（3）选择合适工具建立数学模型.

（4）解决模型中的数学问题并找出所有答案.

（5）根据实际意义对答案进行取舍，选择正确答案.

三、初中数学常见模型

1.方程模型

在现实生活中有许多量与量相等关系的问题，可采用建立方程组的方法解决.

[例1]某社区为响应“绿色生活，美丽家园”的号召，计划种植A、B两类植物来美化小区环境，若种植A类植物3 m2，B类植物2 m2，共需420元;种植A类植物1 m2，B类植物3 m2，共需350元，求：该社区种植A类植物1 m2和种植B类植物1 m2各需多少钱？

解析：按照上述建模方法，分析题意，可设种植A类植物1 m2需x元，种植B类植物1 m2需y元.再由题目中的两个等量关系列方程组即可解决问题.

2.函数模型

现实生活中还会涉及不同变量之间制约性关系的问题，使用函数可以解决此类问题.

[例2]为迎接六一儿童节，某商场购进若干件单价为20元的童装，若规定销售单价不低于每件20元，不高于每件50元，销售一段时间后发现：当销售单价为40元时，平均每月销售量为70件;当销售单价每降低1元时，平均每月能多售出2件.设销售单价为x元，平均月销售量为y件.

（1）求y与x的函数解析式，并写出自变量x的取值范围;

（2）求月销售利润w与售价x之间的函数解析式;

（3）当销售单价为多少元时，销售这种童装每月获得利润最大？最大利润是多少？

解析：分析题意可得到销售模型，利用“月销售量=原销售量+降价后增加的销售量”即可列出对应的函数关系式;利用“月销售利润=（单件售价-单件进价）×销售数量”列出关系式;把每月利润最大问题转化为求二次函数的最值问题来解决.

本题的数学模型是二次函数[y=ax2+bx+c]与一次函数[y=kx+b]的函数模型.

3.几何模型

几何在日常生活中的应用十分广泛，如道路桥梁设计、建筑、航海等方面经常涉及一些图形的性质，需要用数学知识建立几何模型，再分析计算解决实际问题.

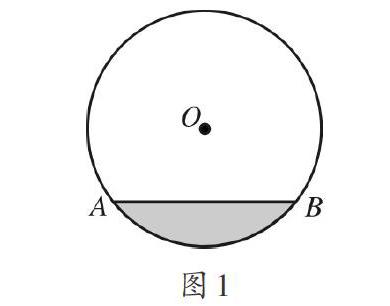
[例3]一下水管道的截面如图1所示.已知排水管的直径为100 cm，下雨前水面宽为60 cm.一场大雨过后，水面宽为80 cm，求水面上升多少？

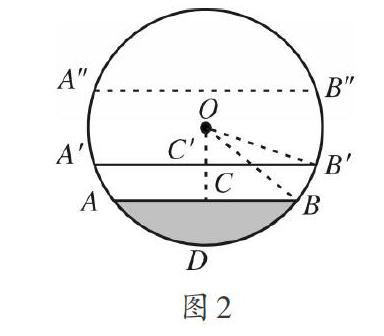
解析：如图2，可作半径[OD⊥AB]于C，连接OB，再用垂径定理和勾股定理进行相关计算.本题的分析过程就用到了“圆”这个几何模型.

4.不等式模型

[例4]某市为了提升菜篮子工程质量，计划用甲、乙种车辆共40辆调拨不超过305吨肉制品和325吨蔬菜补充当地市场.已知一辆甲型车可运肉制品8吨和蔬菜10吨;一辆乙型车可运肉制品7吨和蔬菜5吨.

（1）符合题意的运输方案有几种？请你帮助设计出来;

（2）若一辆甲型车的运费是1000元，一辆乙型车的运费为800元，试说明（1）中哪种运输方案费用最低？最低费用是多少？

解析：设安排甲型车x辆，乙型车（40-x）辆，再结合题目的不等量关系列出不等式组进行求解;由“总费用=甲型车的费用+乙型车的费用”建立一次函数模型，利用一次函数及其增减性可解决最低费用问题.本题就用到了不等式模型和一次函数的模型来解决实际问题.

四、建模思想在初中数学教学的渗透与应用

1.应用于概念教学

数学概念具有一定的抽象性，学生在理解数学概念时存在一定的难度.对此，教师可在概念教学中渗透建模思想，以促进学生更好地理解数学概念.

例如，在教学反比例函数概念时，教师可结合生活实例渗透建模思想为学生创设良好的理解情境.如小王在篮球场打完篮球准备回家，如果小王的家与篮球场距离2000米，那么小王回家花费的时间t与平均速度v之间的关系表达是怎样的？将学生分为若干小组，引导学生应用数学建模思想小组合作研究相关的关系式，进而理解反比例函数的概念.

2.应用于函数教学

在初中数学中，函数知识占据着较大的比重，它还是中考数学必考的知识点，最重要的是它与现实生活存在着紧密联系.发挥函数知识的作用来解决实际问题，是函数教学的重难点.函数与方程的应用非常相似.初中生在掌握函数具体问题所涉及的数量关系方面，缺乏建模意识，这对于他们有效解决函数相关问题具有不良影响.对此，教师要重视对学生建模思想的培育，在解决函数问题的过程中帮助学生明确建立函数模型的方式，引导学生利用数学模型有效解决现实生活中的相关问题，提高学生解决实际问题的能力.

例如，在教学二次函数应用的相关知识时，教师应告知学生函数模型与方程模型的一致性，及两者存在的显著差别是函数模型表示的是两个变量的关系，然后与学生共同探讨旅社客房的问题.如：有120间客房的旅社，一间客房的租金是160元，几乎天天满房.在进行市场调查之后发现，如果将每间客房的租金提升10元，那么客房的出租数量也会随之减少 6间.在不过多思考其他因素的前提下，将客房租金提升到多少客房的日租金可以实现最大化？要解决这一问题，建立函数模型是非常必要的.但并不是所有学生都具备建模的能力，这时需要教师发挥引导作用，引导学生对题目中的数量关系进行分析，建立正确的函数模型，进而解决问题.

通过以上几个例子可以发现，建立函数模型可有效解决函数实际问题，对于学生来说，只有具备了一定水平的建模能力，才能自主地解决与函数相关的问题.因此，教师需要发挥自身的引导作用，帮助学生逐渐形成建模思想与意识.

总之，在初中数学教学中，建模思想的作用是无可取代的，它不仅能极大地提高学生的学习兴趣与热情，提升学生的学习效率，还能培养学生的实践应用能力.

[   参   考   文   献   ]

[1]  雷秀梅. 初中数学新课教学中渗透数学思想的策略研究[D].成都：四川师范大学，2018.

[2]  翟远. 基于数学建模思想的初中数学应用题的教学研究[D].桂林：广西师范大学，2019.

[3]  李静. 初中数学教学中学生数学建模素养的培养策略[J]. 华夏教师，2019（17）：9-10.

[4]  岳本营. 例谈初中数学教学中建模思想的培养[J]. 数学学习与研究，2014（6）：26.

[5]  于虹. 初中数学建模教学研究[D]. 呼和浩特：内蒙古师范大学，2010.

（責任编辑 陈 昕）