扣紧“问题链”让数学思维拾级而上
张桃芳
[摘 要]教师利用“问题链”开展教学,能够激活学生数学思维.学生对“问题链”有主动探究的欲望,能够形成学习驱动力.数学教学中,教师可基于学情设计“引入式问题链”,根据教情设计“类比式问题链”,根据教学重点设计“逆向式问题链”,关注生活实际设计“反思式问题链”.“问题链”教学实践探索,有利于提高教学质量.
[关键词]数学思维;问题链;直线
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)05-0005-02
所谓“问题链”,是指一连串的问题链接.这些问题之间有密切的关联性.在数学课堂教学中,“问题链”的合理设计,能够有效激发学生探索思维,培养其良好的数学感知习惯.教师要做好“问题链”的设计,以发挥“问题链”的助学作用.“问题链”设计需要遵循一些原则,要体现梯度性、开放性、目的性等特征.下面以“直线平行的条件”教学为例,谈谈本人的一些做法.
一、基于学情设计“引入式问题链”
学生对同一平面内平行线的定义有一些了解,也能够掌握画平行线的一般方法,教师以此作为教学起点,从学生学习旧知出发,利用“问题链”形式引入,学生会自然进入推导环节.
在学习“直线平行的条件”时,学生对直線平行条件有一定了解,知道“在同一平面内两条没有交点的线组成了平行线”“利用移动三角尺和直尺方法画两条平行线”.为让学生快速进入课堂学习环节,教师可设计 “问题链”:
在利用三角板和直尺画两条平行线时,直尺和三角板都发挥了什么样的作用?用直尺和三角板,你还能够想出“过一点画一条直线的平行线”的新方法吗?如何验证过一点画出的直线平行已知直线呢?如何从角的对应方向展开推演呢?
学生开始思考和讨论,利用直尺和三角板进行操作实践.当学生逐渐梳理了问题,教师继续揭示“问题链”:在同一平面内,假如有两条直线都垂直于同一条直线,这两条直线平行吗?为什么?学生深入研究,学习思维顺利延伸开来.
从“问题链”设置情况能够看出,这几个问题有明显的梯度性、开放性等特征.学生在思考和实践操作中逐渐进入问题核心,对学习内容进行对接性思考,有效激活数学思维.
二、根据教情引入“类比式问题链”
教师应从启迪、引导、类比、综合等角度展开思考,及时揭示“问题链”,促使学生能够尽快进入发现问题、提出问题、分析问题和解决问题等学习环节.教师通过设问、追问、反问等“问题链”方式展开调度,自然引导学生展开“操作—观察—思考—归结—抽象—建模—内化”学习模式,在问题整合过程中内化认知.
要使“问题链”与教学内容形成高度切合,教师就要对教学操作路径进行细致规划.首先,对教学内容进行深度研读.“直线平行的条件”涉及的数学概念比较简单.“同位角相等,两直线平行”“内错角相等,两直线平行”“同旁内角互补,两直线平行”,这些都是教材内容范畴.教师在具体教学时,需要对这些内容进行推演性展示,让学生自然建构认知.其次,教材设置例题讲解、实践活动、训练任务等栏目,教师要在案例对接中揭示“问题链”.如,集中展示判断平行线的方法时,教师可设计“问题链”:
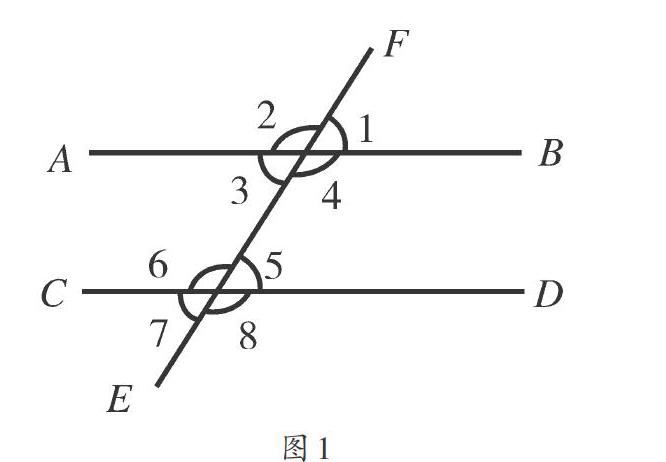
判断两直线是否平行,有哪些方法?你能够利用具体操作进行展示吗?如果给出具体的直观图示(如图1),你能够结合图示中的角的关系展开解读吗?
学生根据问题设计展开思考和操作,课堂学习进入探究环节.
教材分析是“问题链”设计的基础,学生自行解读教材的能力还不够,教师需要做出更多指导示范.利用精巧的“问题链”展开具体引导,能够促使学生尽快启动数学思维,自然进入到学科探究环节.
三、根据教学重点设计“逆向式问题链”
“直线平行的条件”教学中,教师会将“直线平行的条件的应用”“选择适当判断直线平行的方法进行说理”等内容作为教学重点和难点来对待.在教学推演中,教师很快就会发现,“应用”要比“说理”更难,学生大多能够明白其中的原理,但要结合具体实例展开演示,还是存在一些操作问题.为此,教师就可以设计“问题链”:
在同一平面内,两条直线平行的条件判断,涉及同位角、内错角和同旁内角,这些角的位置很清晰,如果给你一个不规则多边形的白纸,让你折叠出两条平行的直线,你有几种操作方法?如何判断你折叠的两条直线是不是平行线?如何判断你同桌折叠的两条直线是不是平行线?
学生积极展开思考,结合具体操作进行深度讨论,课堂学习气氛十分活跃.
“直线平行的条件”有比较固定的法则可以套用,教师利用逆向性问题进行调度,给学生提供更多思考的启示.第一个问题问有多少种操作方法,给学生提出更多挑战,启发学生不能满足从一个角度进行思考,要学会从更多角度思考.第二个问题要求判断自己折叠的两条直线是不是平行线.如果是平行的,需要给出正确的推断;如果是不平行的,也要给出不平行的解释.这对学生来说增加了思维难度.第三个问题是对同桌操作进行类似推断,能够延伸其学习视角,从更多方向展开关注.“问题链”设计和应用的关键是贴合性,贴近学生思维、贴近学生生活、贴近学科实际、贴近教材内容,这样的设计和调度效果才会更好.
四、关注生活实际设计“反思式问题链”
数学学科教学与生活有太多关联点,教师在设计“问题链”时,需要联系学生生活实际,让学生结合学习内容进行生活对接.学生学习数学大多没有主动反思的意识,教师在学生学习过程中,不妨以“问题链”形式,让学生展开反思,对学习认知进一步内化,对数学实践展开进一步探索.
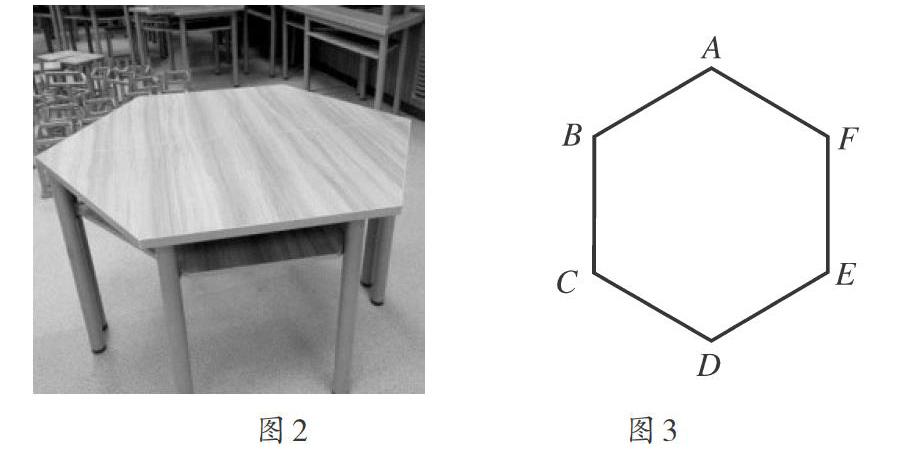
“直线平行的条件”在生活中有更多应用,教师可利用一些生活案例展开教学.如,六角形的桌子(如图2),其桌面呈现六角形(如图3),如何判断其中两条边是平行的呢?你能够结合角的分析说说判断过程吗?由这个案例的推演可以想到更多相关对应角的操作吗?如何从生活实践中归结直线平行条件呢?
学生开始了深入思考.教师引导学生观察六角形桌面,让学生自行寻找思维切入点,对关联数学概念进行对应提示,学生数学思维顺利启动,在主动探索中完成相关问题的解答,自然形成关联性认知.
数学学科和学生生活有密切关联,教师结合具体生活案例设计“问题链”,引导学生分析,帮助学生展开学习和探索,学生会在具体操作中获得丰富学习感知和体验.
“问题链”是问题的集合,教师针对教学内容和教学进程的实际需要设计“问题链”,能够有效引导学生思考,提高学生的能力.
[ 参 考 文 献 ]
[1] 唐恒钧,黄辉.数学问题链教学设计与实施的三个关键[J].中学数学,2020(5):78-80.
[2] 倪朝辉.构建有效“问题链”,助推课堂深度教学[J].数学教学通讯,2019(36):43-44.
(责任编辑 黄桂坚)

