综合评价结果稳健性的偏序集分析

岳立柱，施光磊，陆 畅

（1. 辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105；2. 辽宁工程技术大学 管理科学与工程研究院，辽宁 葫芦岛 125105）

0 引言

有效评价是任何学科取得成功的关键因素，尤其是在需要处理大量信息以及知识作为构建的领域[1].在综合评价的过程中，决策者往往面临着大量的不确定性.因为决策者经常面临复杂的问题，解决这些问题往往涉及多学科知识，包括技术、经济、环境和社会，以及政治和法规方面[2].在这样的环境中做出决策往往是一项艰巨并且充满风险的工作，因此充分考虑评价各环节的各种不确定性，提升模型的稳健性是评价领域不可缺少的任务.

评价的稳健性源于评价过程中的不确定性.从系统视角可将不确性划分为内部不确定性和外部不确定性[3].内部不确定性与决策问题的构建和分析有关，来源于对决策问题、模型设定和输入数据的不完全理解.外部不确定性与决策环境的性质有关，即某一特定行为的后果，超出了决策人员的掌控范围.在产生来源上又可以划分为模糊不确定性和随机不确定性[4]，关于这两方面的研究不仅广泛而且较为深入，是不确定性研究的典型代表.

模糊不确定性的处理方式不仅研究较早，而且广泛深入.模糊数和语言变量这两个概念为模糊多准则分析奠定了基础.决策者使用一组语言变量（例如不重要的、重要的、非常重要的、极其重要的）来描述评价准则之间的相对重要性程度[5].应用语言变量的重要性在于它天然具有表达和处理不精确或模糊陈述的能力.例如，WANG Y J[6]提出模糊SAW 模型，求解具有语言等级和不完全偏好信息的多准则决策问题；CHEN T[7]提出区间二型模糊集的SAW方法；CHEN S M[8]等及HONG D H[9]等基于Vague 集研究了综合评价方法，该模型能够反映正面和反面的信息，比模糊集提供更多、更全面的信息.因此，DUBOIS D[10]认为模糊集理论为决策分析中的数值方法和定性方法提供了一个桥梁.不过，ZHÜ K[11]指出在复杂和不确定的环境中，具有清晰数字的层次分析法比模糊判断更有效.模糊数学处理不确定性广泛应用，尽管其受到了批评，但根据KUBLER S[12]等对模糊层次分析法的文献调查（回顾了2004年至2016 年间发表的190 篇学术期刊文章）可以看出，采用模糊数学应对不确定性的做法将持续增长.

为提升模型的稳健性，学者们对指标数据的随机性进行深入研究.概率分布或随机多准则决策分析方法显式地将不确定性概念合并到决策规则中，即使用概率分布而不是单个数字来描述每一个备选方案的总体表现.多属性效用理论[13]（MAUT），是专门为处理不确定信息而开发的.然而，MAUT 在实践中难以使用[14]，因其通过不为人所知概率分布来指定不确定的结果[15]，需要过多的时间和较高的认知负担才能得出个体的效用函数[16].随机多属性可接受性分析[17-18]（SMAA）已在多标准决策分析中流行，用于处理指标数据和权重不确定性.它考虑了整个可能的权重空间，将方案间占优概率转换为对于空间“大小”的比值，同时还能兼顾指标取值的不确定变化.SMAA 最近被引入到综合指标领域，例如，DOUMPOS M[19]等使用这种方法创建一个综合指数，评估1 200 家跨国银行在不同加权情景下的整体财务实力.GRECO S[20]等建议用SMAA 来处理综合指标中的加权问题，因为它考虑到不同决策者偏好.

在过去的几十年中，有关处理不确定性信息的综合评价方法迅速增长，为实践决策提供了辅助支撑.当前不确定性的研究大多集中于系统输入的不确定性，例如，学者们提出了模糊综合评价、随机综合评价、直觉模糊综合评价、二元语义综合评价，从系统论的视角来看，均侧重话语系统输入的不确定性研究.由于一个系统的输出是另一个系统的输入，因此开放系统的输出同样具有不确定性.所以，单纯的输入控制显得不足，需要从输出端对不确定性进行控制.偏序方法不假定数据间是否具有线性关系，也不假定数据分布特征[21]，适用于基数、序数、语义等多种数据，具有鲁棒性佳的优点.由于偏序Hasse 图中的确定性比较结果不受输入端不确定信息的影响，因此，用其可以评判传统评价结果的稳健程度.将传统评价升级为偏序评价，应用Hasse 图表达评价输出，通过其确定性比较关系便能对传统综合评价结果的稳健性予以分析.

1 综合评价模型

综合评价（Comprehensive Evaluation，CE）也称多指标综合评价.广义的综合评价是指对多指标进行综合的一系列有效方法的总称，此时的综合评价与多准则决策（MCDM）含义等同；狭义的综合评价指集结函数为线性或者拟线性的综合评价，是广义综合评价中最基础和最核心的部分.本文选择狭义综合评价，一是狭义综合评价是广义综合评价的基础；二是该方法应用广泛，在专家系统文献中得到了广泛的应用，但其决策规则透明度高，意味着他们的工作很容易被非专家、以及来自决策领域之外的个人所掌握.

（3）数据预处理.评价准则除了指标单位不同之外，指标值也有不同的意义，数值愈大愈好，称为效益指标；数值愈小愈好，则称为成本指标.为进行n个指标的综合比较，须对指标方向及单位进行归一化处理；

（5）方案排序.根据综合值f(x) 大小进行排序，一般采用值愈大表示方案愈佳.

综合评价属于多准则决策领域中最基础的研究部分，也是现实生活中应用最为广泛的模型.但从测量学的角度看，多指标代表着“多次”或多维测量，而综合指标意味着“单次”测量，因此综合指标具有天然的不稳健性.综合指标发展的历史表明，将复杂、动态、多层面和充满歧义的现象所相关的信息转化为一维指标是项复杂的系统工程.当评价过程充满着随机和模糊等不确定性时，评估结果的可靠性将耗费大量的认知资源，严重干扰当前决策判断、诱发决策风险.

2 综合评价模型的偏序集表示

2.1 线性模型的偏序表示原理

偏序集详细内容见文献[22]～文献[25]，仅将核心思想和必要结论作重述.

定义1设R是集合A上的一个二元关系，若R满足：

（1）自反性 对任意x∈A，有xRx；

（2）反对称性（即反对称关系） 对任意x,y∈A，若xRy且yRx，则x=y；

（3）传递性 对任意x,y,z∈A，若xRy且yRz，则xRz.则称R为A上的偏序关系[22].

鉴于传统偏序方法无法处理偏好问题.根据决策者对指标重要性排序获得权重空间，通过对评价矩阵进行累加变换，将权重空间嵌入评价模型，成功表达了决策者偏好问题[23-24].

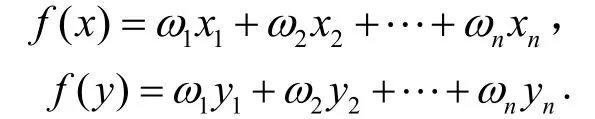
定理1给定评价集，设准则权重，若

根据式（1）构造能够反映权重差异的偏序关系，即

若偏序关系为特殊的全序关系，则矩阵R为可达矩阵.偏序关系矩阵存在信息冗余，需要将其简化为Hasse 矩阵HR文献[25]给出了二者的转换公式

式中，I为单位矩阵；运算符号∗为布尔乘法.

根据Hasse 矩阵绘制Hasse 图.有关偏序决策的研究起始于Hasse图性质研究.著名Dilworth定理[26]，即最大反链的大小等于覆盖所有元素的最小链数，该定理描述了Hasse 图的基础性质.最大层级的大小通常称为Hasse 图的“高度”，最大层级的长短通常称为Hasse 图的“宽度”，该定理的扩展被用于正式组织的研究[27].

应用偏序Hasse 图表达评价系统输出是建立稳健机制的核心和关键.偏序Hasse 图与传统表达输出存在本质差异.偏序Hasse 图表达二维信息，综合指标本质仍为单维信息.而单维信息经常“扭曲”多维序关系，通过偏序Hasse 图能够有效表达多维序关系，揭示二者在表达多维序信息上的根本差异.

2.2 非线性函数偏序表示的判定定理

当前偏序表示的评价函数为线性函数，实践中可以转换为非线性函数的评价函数也是常见的多指标集结方式.需要给出具有一般意义上综合评价函数的偏序表示方法.

定理2令n元实函数若存在函数使得

式中，g为单调增函数，ih为n元实函数.当时，对有

证明令根据式（6）可知

又g为单调增函数，故

由式（7）和式（8）可知式（6）成立.证毕.

根据定理2 应用偏序集能表达集结算子.例如，式（5）中若g(t)=t，i hi(x)=x，则f(x)为简单线性加权算子（WAA）；若g(t)=t，hi(x) =yi，其中yi表示向量x= (x1,x2,…,xn)第i大分量，则f(x)为有序加权算子（OWA）.

3 基于Hasse 图的稳健性评价指标

3.1 设计基础

用Hasse 图表达综合评价的输出结果具有良好的稳健性.稳健机理在于偏序Hasse 图能够表达确定性和不确定性信息，即确定性比较关系对不确定性“免疫”，不确定性比较关系对确定性“敏感”.从Hasse 图中提取稳健和非稳健的评价信息，为解读评价结果提供增值服务.

在计算机科学中，找到偏序集的线性扩展链的算法叫做拓扑排序.将偏序集的所有线性扩展链集合称之为线性扩展集.偏序集评价方法在线性扩展集上构造了方案排序方法.根据图1 可知，满足偏序关系的全排序共有3 种

根据线性扩展进行方案比较的思路，见图2.

图1 Hasse 图Fig.1 Hasse

图2 线性扩展链Fig.2 Linear extension chain

当前对线性扩展的研究均假定每条扩展链出现的概率是相等的.本例中有3 条扩展链，每条出现的概率为1/3.方案全排序由秩均值来实现.例如本例中方案D在第3 层出现了一次、在第2 层出现了1次， 第 1 层 出 现 了 一 次， 秩 均 值同 理，可 得.根据秩均值的线性关系，排出的方案优劣顺序为

与常规排序方法不同的是，根据线性扩展链能够给出方案比较的概率.对于不可比方案的比较概率值小于1，例如C大于D的概率

3.2 方案和层级的不确定性指标构建

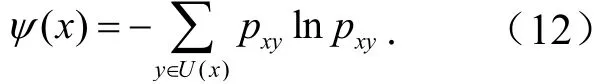
由于存在|U(x)|=0，将式（13）进行变换，即

当式（12）参数未知时，可采用式（13）近似计算.令BA，则集合B的不确定指数为

当式（14）计算困难时，采用如下近似公式

综上，给出应用偏序集表示和进行Hasse 图分析的操作步骤

第一步评价函数的线性化处理，使其满足线性表达条件.

第二步通过累加变换，提取权重偏好信息.

第三步获得偏序关系矩阵，计算Hasse 矩阵.

第四步根据Hasse 矩阵，绘制Hasse 图.

第五步由式（12）和式（14）或（式（13）和式（15））进行稳健性分析.

4 实例分析

4.1 指标数据

文献[30]探讨砂轮磨料问题，砂轮是由结合剂将磨料固结成一定形状，具有一定强度的固结磨具.选择砂轮磨料有8 个方案，分别为碳化钛（A1）、碳化钨（A2）、立方氮化硼（A3）、氧化铝（A4）、合成多晶金刚石（A5）、碳化硅（A6）、碳化硼（A7）和钇稳定氧化锆（A8）.砂轮磨料选择准则有诺普硬度C1（单位为KHN）、弹性模量C2（单位为GPa）、抗压强度C3（单位为MPa）、抗剪强度C4（单位为MPa）、导电率C5（单位为W/mk）、断裂韧性C6（单位为MPa·m1/2）、材料成本C7（单位为USD/kg）.所有这些标准除了砂轮磨料成本外，都是效益型的.砂轮磨料选择问题的原始数据见表1.

表1 砂轮磨料选择材料Tab.1 grinding wheel abrasive selection materials

按文献[30]w3≥w1≥w4≥w2≥w7≥w5≥w6的权重顺序排列，数据标准化得到表2.

表2 依权重顺序整理后的指标Tab.2 indexes sorted by weight order

4.2 评价结果的偏序集表示

根据式（2）对方案进行两两比较得到偏序关系矩阵.根据式（4）由偏序比较关系矩阵得到Hasse矩阵，进而绘制Hasse 图，见图3.

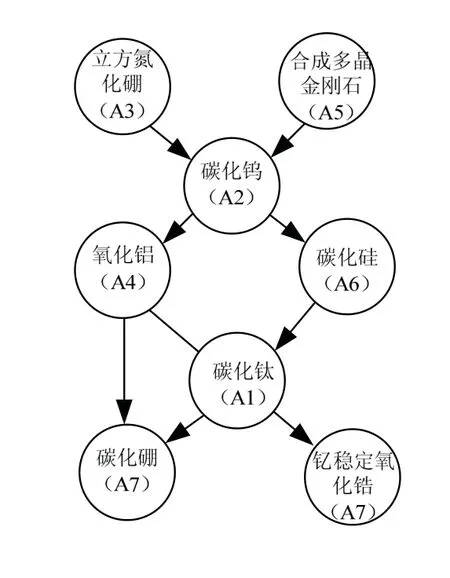
图3 8 种方案Hasse 图Fig.3 Hasse diagram of eight schemes

由图3 可以看出有4 对方案不可比，即（A3，A5）、（A4，A6）、（A4，A1）和（A7，A8）.不可比方案表明，在给定的权重空间内，二者的排序一定可以“翻转”.可比方案表明在给定的权重空间内，二者的排序关系稳健不变.

4.3 仿真模拟

为检验和揭示Hasse 图排序的稳健性，应用Python3.6 语言编写仿真程序.程序包括：① 按照权重秩次关系，随机生成了10 000 个7 维的权重向量，或者说在给定权重空间内，抽取了10 000 个权重样本；② 权重向量乘以方案向量，即10 000 个权重向量乘以8 种砂轮磨料数据，共得到10 000 行8 列的评价数据（第i行第j列，表示第i个权重向量与第j个方案向量的乘积）；③ 对模拟评价数据进行两两列比较，最终模拟结果整理为表3.

表3 权重随机变动下的砂轮磨料比较结果Tab.3 comparison results of grinding wheel and abrasive under random weight variation

表3 数字有力反映出模拟结果与理论完全符合！Hasse 图性质表明，对于可比方案，给定权重秩次约束条件下，无论权重如何变动，二者比较关系不变.例如，在Hasse 图中A3 优于A2，该性质表明无论模拟的次数有多少，前者优于后者的概率一定为1.仿真结果表明方案A3 优于方案A2 发生次数为10 000 次，前者优于后者的概率为100 %，这与理论预期完全一致.

对不可比方案的仿真结果，不仅凸显了Hasse 图性质分析的独特性，同时揭示了仿真模拟的不足.图3中有4 对方案不可比，这些方案的模拟比较结果，理想取值应大于零且小于1.例如，在10 000 次模拟中方案A1 的综合值大于A4 发生了7 926 次，即估计前者大于后者的概率为79.26%，A7 评价值大于A8 共发生了9 929 次，频率为99.29%.

尽管A5 大于A3 共发生了10 000 次，模拟概率为100%，但图3 表明二者不可比.如果在权重空间内取指标3 的权重为1，其它指标权重为0，则A3 优于A5.结果表明，随着模拟结果的增加，会使得A5 大于A3 的模拟概率一定不为1.这表明对不可方案的仿真结果会受到模拟次数的限制，可比方案的模拟结果与仿真次数无关.

4.4 评价结果的稳健性分析

在本例中对给定的权重空间无论选择怎样的权重，通过偏序Hasse 图均可以识别最佳方案集合、识别确定和不确定的比较关系、计算各方案和层的不确定程度.具体如下：

（1）识别可比方案.本例中A3 和A5 均优于其它所有方案，表明最佳方案一定在{A3，A5}中产生，权重顺序保持不变的条件下，无论权重怎样变动，最佳方案候选集{A3，A5}不变.

（2）识别不确定方案.尽管模拟结果和文献[30]结果，一致得到A5 优于A3，在Hasse 图中二者为不可比方案，表明存在A3 优于A5 的可能.例如，如果第三个指标上原料充足，或者预计未来成本下降更快，一般会选择A3 为最佳；若要兼顾多个指标，当其它指标权重也占较大比值，最优选择A5更为稳妥.

（3）根据式（13）和式（15）计算各方案和Hasse 图的不确定程度，计算结果见表4.

表4 方案与层的不确定程度Tab.4 uncertainty degree of scheme and layer

从表4 中可以看出方案A4 为最不稳定元素，即随着权重变动，方案排名变动程度最大.方案A2为最稳定元素，即随着权重变动，该方案排名不变.最不稳定层为{A6，A4}，最稳定层为{A2}.

5 结论

应用偏序集表示的综合评价能够分析评价结果的稳健性.该方法不仅能单独使用，还可以与其他多准则决策方法结合应用.研究结论如下：

（1）针对当前综合评价的表示仅限于线性函数的弱点，在线性函数偏序表达相关定理基础上，结合函数变换特征，证明了非线性函数可以偏序表达的判定条件.该结论为分析非线性综合评价的稳健性提供了理论支持.

（2）围绕偏序Hasse 图建立了方案和层的不确定度量指标.通过该指标能够比较方案排名的不确定性，不确定性越高表明在综合评价过程中随着权重的变化，该方案排名变动的可能越大，即对权重变动的敏感性越高.

（3）实例分析体现了偏序Hasse 图在综合评价分析中的独特价值.与仿真模拟比较表明，Hasse 图中可比方案的仿真结果与仿真次数无关，即不随仿真次数的改变而变动，凸显了可比方案的稳健性.Hasse 图中不可比方案的仿真结果与仿真次数有关，仿真结果会受到模拟次数的限制，因此，通过Hasse 图能够发现仿真分析的不足.