玄武岩纤维树脂混凝土填充结构机床横梁优化及性能分析

于英华，曹茂林，徐 平，高 级

（辽宁工程技术大学 机械工程学院，辽宁 阜新 123000）

0 引言

随着现代加工制造业向着高效率、高精度、高自动化程度的方向发展，要求机床有更高的静、动态性能和轻质性.利用性能优异的新型材料制造机床基础件是行之有效的途径,这也成为国内外学者研究的重要课题[1-4].BFPC 是以玄武岩纤维为增强相的树脂混凝土复合材料，该材料除具备其他纤维增强树脂混凝土所具有的线膨胀系数小、高阻尼、吸振强外，还具有和易性好、耐腐蚀性高和环保可持续发展等优势，因此，它被认为是一种很有发展前景的机床基础件新材料.课题组依托国家自然科学基金项目对适合制造机床基础件的BFPC 最优组分配比和BFPC 整体结构床身、立柱和龙门框架及填充结构工作台、立柱进行了设计优化及性能仿真分析[3-13].本文对BFPC 填充结构横梁的结构进行设计优化，并对其静、动态性能及轻量化进行分析，验证BFPC 填充结构横梁的可行性和优越性，为发掘BFPC 在机床基础件中应用的潜能，探索提高机床静、动态特性和轻量化的新途径提供参考.

1 原型横梁选取及性能分析

1.1 原型横梁选取

选取桥式龙门加工中心的移动式横梁为研究对象，结构见图 1，其外形尺寸：1 100 mm×375 mm×225 mm，其内壁上设有横向加强筋和纵向肋板，厚度为20 mm，横梁导轨安装面的壁厚为27 mm，其余壁厚为均22 mm.

图1 原型横梁结构（单位：mm）Fig.1 prototype beam structure（unit:mm）

1.2 原型横梁的静、动态性能分析

对原型横梁进行静、动态性能分析以确定其在典型工况下的变形、应力、前两阶固有频率、最大谐响应幅值以及质量，以此作为后文对BFPC 填充结构横梁优化时的约束条件和优化效果比对.

由于当滑鞍位于横梁中间位置时横梁的受力变形将会最大，为此本文以此时对横梁受力分析，并选取硬质合金端铣刀对称铣削低碳钢为典型工况，该典型工况下所采用刀具参数和切削用量见表1.

表1 刀具参数和切削用量Tab.1 tool parameters and cutting parameters

横梁受到的载荷有：横梁自身重力G0、滑枕重力G、刀具铣削力Fc，见图2.

图2 横梁受力分析Fig.2 stress analysis of the cross beam

利用经验公式计算铣削力Fc及其各分力Ff、Fo和FfN，根据图中坐标可得出切削力和重力的作用点矢量为

式中，i、j、k分别为X、Y、Z轴的单位向量.

建立原型横梁三维模型，横梁材料为铸铁，其密度为7 280 kg/m3、弹性模量138 GPa、泊松比0.25、阻尼比0.6%.用Workbench 建立横梁的有限元模型，模型中包含26 257 个单元，85 187 个节点.

根据实际情况对横梁添加载荷和约束，见图3，主轴箱和滑鞍的重力转化到横梁导轨中心接触面的载荷A，切削力载荷B、主轴箱和滑鞍的重力转化到横梁导轨中心接触面的力矩C、切削力转化到横梁导轨中心接触面的力矩D、横梁自身重力E，由于原型横梁固定在床身上，因此将横梁与床身的安装接触面施加固定约束F.

仿真分析得到横梁的应力和变形见图4.由图4可知原型横梁的最大等效应力为6.026 7 MPa，最大静变形为4.667 1 μm.

图3 载荷和约束Fig.3 loads and constraints

图4 应力和变形Fig. 4 stress and deformation

机床基础件共振一般发生在低阶模态下，故对横梁前两阶模态进行分析.对模型进行求解，分析结果见图5.

图5 前2 阶振型Fig.5 first second order mode

由图5 可知，模型的第一阶模态固有频率为389.7 Hz，振型为沿X轴方向振动；第二阶模态固有频率为582.15 Hz，振型为绕Y轴方向的扭转.

由模态分析的结果可知原型横梁前两阶固有频率，为使谐响应分析结果完全包含结构的前两阶频率，设置激振力的频率为300～1 500 Hz，横梁约束条件与静力分析相同.在ANSYS软件的Harmonic Response 设置求解的载荷步数为500，求解的方法为Full，以此分别计算横梁导轨中心在X、Y、Z方向的频率响应曲线.

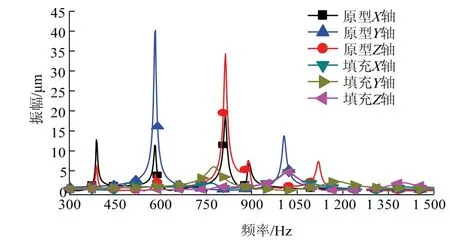
分析结果见图6，原型横梁在X、Y、Z轴方向的谐响应振幅分别为18.362 μm、38.242 μm、32.269 μm.

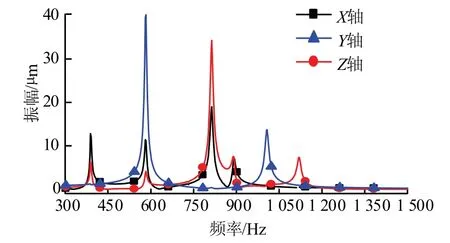
图6 谐响应振幅Fig.6 harmonic response amplitude

2 BFPC 填充结构横梁初步设计

设计BFPC 填充结构横梁时，首先，需保持其外形尺寸及其关联尺寸不变以保证机床的整机结构和装配关系不变；其次，需要满足浇注的工艺性要求和刚度要求.初步设计BFPC 填充结构横梁见图7，即其由厚度为t1、t2的钢板焊接构成外壳体，而后在其中填充BFPC 材料.

根据BFPC 填充结构横梁应满足抗弯、抗扭刚度及轻质性的设计要求来确定变量t1、t2的取值范围.

图7 BFPC 填充结构横梁（单位：mm）Fig.7 BFPC filling structure cross beam（unit:mm）

2.1 抗弯刚度对BFPC 填充结构横梁壁厚要求

根据材料力学相关理论，应用平行轴定理计算BFPC 填充横梁对X轴截面的抗弯惯性矩，见图8将BFPC 填充结构横梁截面划分为11 个矩形区域，各区域形心的纵坐标分别为yc1～yc11.

图8 BFPC 填充结构横梁划分截面的X 轴形心距Fig. 8 X axis center distance of cross section of BFPC filled structure beam

BFPC 填充结构横梁截面矩形区域截面的尺寸标注见图9.可得形心距为

式中，Ai为各划分区域的面积，各划分截面区域1～11 的惯性矩为

图9 BFPC 填充结构横梁截面尺寸标注Fig. 9 BFPC filling structure cross-section dimension

按照表2中的BFPC材料性能参数进行计算求解.

表2 材料参数Tab.2 material parameters

所以BFPC 填充结构横梁截面对X轴的抗弯刚度为

同理可求得，BFPC 填充结构横梁截面对Y轴的抗弯刚度为

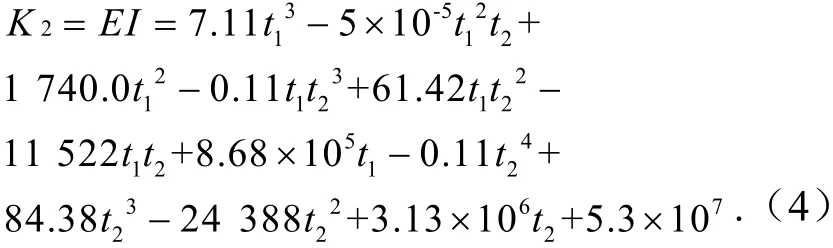
原型横梁对X和Y轴的抗弯刚度可根据其结构尺寸（见图1）进行计算，分别为K3=2.6×107N·mm2和K4=8.95×107N·mm2.

要求设计后的BFPC 填充结构横梁对X轴和Y轴的抗弯刚度分别大于或等于原型结构，即应使

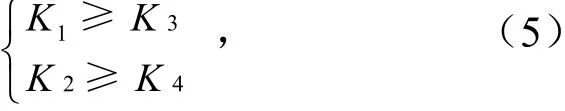
联立式（3）～式（5）并化简得

2.2 抗扭刚度对BFPC 填充结构横梁壁厚要求

BFPC 填充结构横梁截面的抗扭刚度为

式中，G为BFPC 材料的剪切模量，Pa；Ix为横梁截面对X轴的惯性矩，mm4；Iy为横梁截面对Y轴的惯性矩，mm4.

同样原型横梁的截面抗扭刚度可由图1 尺寸计算得：K5=4×107N·mm2.

为使设计后的BFPC 填充结构横梁抗扭刚度大于或等于原型横梁，即应使

联立式（7）和式（8）并化简得

2.3 轻质性对BFPC 填充结构横梁壁厚要求

对于移动式机床基础件提高其轻质性可以带来以下优势：其一，可以提高其快启快停的响应性、从而提高机床定位精度、加工精度及加工效率；其二，可以提高其低速运动的平稳性，即降低或抑制其低速爬行现象；最后可以降低其移动过程中所需要的驱动功率，降低机床运行的能耗，提高机床的环保性.而本文所设计的横梁为一个运动的机床基础件，因此，提高其轻质性大有裨益，为此设计BFPC 填充结构横梁应使其质量M2小与或等于原型结构横梁质量M1，即

在建模软件中通过定义原型横梁的密度，进而求得原型横梁的质量M1为305 kg.

根据BFPC 填充结构横梁结构尺寸可求出其质量，即可得到轻质性对壁厚的要求为

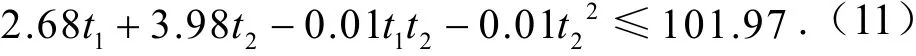
2.4 初步确定BFPC 填充结构横梁设计变量尺寸

在Matlab 软件中联立式（6）、式（9）、式（11），确定t1、t2取值范围，见图10.图10 中阴影区域为变量t1、t2的可行域：9.768 mm

图10 变量可行域Fig. 10 variable feasible domain.

3 BFPC 填充结构横梁优化设计及性能分析

3.1 设计变量响应曲面分析

在ANSYS 软件中设置BFPC 填充结构横梁外壳厚度t1及t2为输入参数，而将BFPC 填充结构横梁的最大静变形、最大静应力、前两阶模态固有频率、导轨中心在X、Y、Z方向的响应幅值及模型质量设置为输出参数.从而求得两个设计变量与各目标函数的响应曲面，分析结果见图11.

由图11（a）可知静变形目标函数和两个设计变量是呈线性关系变化，并且随着两个变量的增大静变形在减小.由图11（b）可知静应力目标函数随着设计变量t1的增大在迅速地减小，而t2的增大静应力基本不变，由此可以看出设计变量t2对静应力这一目标函数影响很小.由图11（c）可知横梁质量目标函数随着两个设计变量t1、t2的增大其质量都在缓慢地增大.

由图11（d）可知第一阶固有频率随着变量t1、t2的增大呈现先增大后减小地变化趋势，且在t1=20.2 mm 和t2=10.1 mm 时达到最大值.同理，由图11（e）可知第二阶固有频率同样随着变量t1、t2的增大呈现先增大后减小地变化趋势，且变化范围很大，说明变量t1、t2对横梁低阶固有频率具有较大影响.

由图11（f）～图11（h）中可知BFPC 填充结构横梁导轨中心X方向振幅随着变量t1、t2的增大而迅速地增大，同时可以看到振幅的变化范围很大；Y方向振幅是随着变量t1增大而逐渐地增大，随着变量t2增大先逐渐地增大，当t2=13 mm 时而又逐渐减小；而Z方向振幅随着变量t1的增大而逐渐地增大，而基本不受t2变化的影响.

图11 设计变量与各目标函数的响应Fig.11 design response of variable and each objective function

3.2 BFPC 填充结构横梁多目标优化

以BFPC填充结构横梁的静变形和静应力不大于原型横梁为约束条件，以横梁的前二阶固有频率最大、导轨中心在X、Y、Z方向的响应幅值最小及质量最小为多目标函数，建立该优化问题的数学模型为

式中，P1和P2为设计变量；g3(P)和g4(P)为BFPC横梁的静变形和静应力；f5(P)、f6(P)、f7(P)、f8(P)、f9(P)、f10(P)分别为BFPC 横梁的前两阶固有频率、横梁在X、Y、Z轴的响应幅值及质量目标函数.

采用筛选法进行优化，设定100 个样本点，并输出3 个最佳优化点.考虑BFPC 横梁的制造工艺，将设计变量进行合理圆整，结果见表3.

表3 优化圆整结果Tab.3 optimized roundness results

3.3 BFPC 填充结构横梁性能分析

运用Workbench 软件对BFPC 填充结构横梁进行静力学分析，模型受到的载荷与约束与原型结构相同，结果见图12.

图12 变形和应力Fig. 12 deformation and stress cloud map

由图12 可见，BFPC 填充结构横梁的最大应力和最大变形分别为3.060 9 MPa 和3.1375μm，比原型横梁的6.026 7 MPa 和4.6671μm 分别降低了49.21%和32.77%.

BFPC 填充结构横梁的前两阶模态见图13，分别为488.39 Hz 和777.35 Hz，比原型横梁的389.7Hz和582.15 Hz 分别提高了25.32 %和33.53%.

图13 BFPC 填充结构振型Fig.13 mode diagram of BFPC filled structure

进一步对原型横梁和BFPC 填充结构横梁进行谐响应分析，结果见图14，可见BFPC 填充结构横梁在X、Y、Z轴3 个方向的最大响应幅值分别为4.623 9 μm、5.614 1 μm 和4.561 1 μm，比原型横梁的18.362 μm、38.242 μm 和32.269 μm 分别降低了74.82%、85.32%和85.86%.

依据前叙确定的BFPC 横梁结构尺寸计算得到其质量仅有283.3 kg 与原型305 kg 相比减轻了7.11%.

图14 两种横梁频响Fig.14 frequency response of two beams

4 BFPC 填充结构横梁实验研究及仿真

为进一步证明仿真分析的可行性及BFPC 填充结构横梁在动态特性方面的优越性，本节将采用实验测试和仿真分析法分别对其自由模态进行研究并将其结果进行对比分析.

4.1 实验研究

为降低实验成本又不失实验结果的准确性，对BFPC 填充结构横梁自由模态的实验研究采用模型实验研究方法，即根据相似理论以1∶2.5 的尺寸比例制造相同材料、相似结构的BFPC 填充结构横梁见图15，其中由4 mm 和7 mm 钢板焊接构成的外壳体中填充的BFPC 材料的组分配比及其制备方法同参考文献[3].

图15 BFPC 填充结构横梁试件Fig. 15 response curve of beam specimen of BFPC filled structure

在横梁试件上、下、前、后端面共设置25 个拾取点.采用单点激励、多点拾取的方法对BFPC 填充结构横梁进行模态实验分析，图16 为实验现场.

为使测试结果更准确，采用多次拾取信号再取其平均值的方法，并在测试软件中设置节点，建立横梁试件模型，并添加模态分析结果.采用Polylscf法进行模态识别，并计算横梁前两阶固有频率、振型，结果见图17 和表4，由图17 可知，试件第一阶振型为绕Y轴方向弯曲，第二阶振型为绕X轴方向弯曲.

图16 实验现场Fig. 16 experimental site

图17 横梁模型振型Fig.17 model mode of the beam model

表4 横梁模型前两阶固有频率Tab.4 first two natural frequencies of beam model

4.2 仿真分析

对所设计的BFPC 填充结构横梁进行自由振动的模态仿真分析，振型及固有频率结果见图18.

图18 仿真振型Fig.18 simulation mode

4.3 实验结果与仿真结果对比分析

根据相似原理和机床模型梁类件弯曲公式[14-15]反推实际结构尺寸的BFPC 填充结构横梁固有频率应为

式中，fni为模型第i阶固有频率，Hz；βi为第i阶固有频率的固定系数；E为弹性模量，Pa；ρ为密度，kg/m3；A为截面面积，m2；l为长度尺寸，m；I为惯性矩，m4.

由惯性矩与长度尺寸及面积与长度尺寸的关系可得，固有频率相似系数cfn应为

式中，cE为弹性模量相似系数；cI为惯性矩相似系；cρ为密度相似系数；cA为面积相似系数；cl为长度相似系数.

由于制造的1:2.5 缩小比例的BFPC 填充结构横梁的对应部分材料与实际尺寸的横梁相同，因此cE=1 ，cρ=1 则，模型的固有频率为，此时实际尺寸的BFPC 填充结构横梁的固有频率fi1应为

转化后的实验结果和仿真结果见表5，对比可知两者的模态振型一致且前两阶固有频率误差分别为在3.04%和9.11%，这验证用仿真分析方法对BFPC填充结构横梁进行动态特性分析的可行性.

表5 实验结果与仿真结果对比Tab.5 comparison between experimental and simulation results

5 结论

（1）通过等刚度和轻量化原理及响应面分析法和多目标优化设计BFPC 填充结构移动式横梁.

（2）仿真分析结果表明：与原型结构机床横梁相比，BFPC 填充结构横梁最大静应力、最大静变形分别降低49.21%和32.77%，且其质量也降低了7.11%；前两阶固有频率分别提高了25.32%和33.53%；在X、Y、Z这3 个方向的谐响应幅值分别降低了74.82%、85.32%、85.86%.证明了BFPC 填充结构横梁在提高机床基础件以及整机静、动态性能和轻质性方面的可行性和有效性.

（3）综合运用试验研究和仿真分析方法对BFPC 填充结构横梁的前两阶模态进行分析并将结果对比分析，结果表明两种方法得出的横梁前两阶模态振型相同，且各阶固有频率误差在允许范围之内，表明两种研究方法结果互为验证，进一步共同证明了BFPC 填充结构横梁在提高机床基础件乃至整机静、动态性能和轻质性方面的可行性和有效性.