波动载荷下弓网载流动态摩擦力模型

陈忠华，贾利明，时 光，回立川，唐 俊

（辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105）

0 引言

在弓网滑动电接触中摩擦是不可避免的，常常对系统的性能产生很大的影响[1].随着列车运行速度的大幅度提高，弓网动态压力载荷变化加剧，由于摩擦而造成的机械磨损和电气磨损问题越来越严重，极大地降低了系统的性能，因此对摩擦力的建模研究变得越来越重要了.

由于摩擦的强非线性以及在滑动过程中所表现出多种特性，关于摩擦力建模的研究一直是国内外学者关注的热点.关于摩擦力模型的研究最简单的是DEN[2]等在1931 年提出的库伦模型，因其结构简单，因而在大部分机械摩擦系统中被广泛使用.STELTER P[3]等在库伦摩擦力模型的基础上提出了Popp-Stelter 模型，这个模型考虑了摩擦的速度相关性，能够很好地解释摩擦系统的自激振动现象.WIERCIGROCH[4]、DAHL[5]等根据摩擦力在加速和减速阶段的不同特性，提出摩擦力的速度滞回特性模型，用以描述摩擦力的记忆特性.CANUDAS[6]等在1995 年提出著名的LuGre 摩擦模型，这个模型几乎可以解释实验中所有的摩擦现象，包括爬行效应、Stribeck 效应、记忆特性等.在摩擦力模型的应用方面，PALLI[7]等基于简化的LuGre 模型建立一个新的摩擦力模型来描述机器人手关节的摩擦力补偿技术.陈剑锋[8]等基于LuGre 摩擦模型提出静态和动态参数辨识及建模方法，获得不同气压、速度下被测气缸的摩擦力模型.张巍[10]等基于接触理论建立直线导轨滑块的受垂直载荷的静力学平衡方程，建立了随外载荷变化的直线滚动导轨副摩擦力模型.文献[2]～文献[6]对摩擦力的研究，主要涉及到摩擦力与位移、速度、加速度等因素的相关性，但未涉及到电流因素对摩擦力的影响，文献[7]～文献[9]对摩擦力的研究，主要涉及到摩擦力在机器人、气缸和导轨等方面的建模，但未涉及到弓网系统方面的建模研究.而关于摩擦力在弓网滑动电接触方面的动态建模研究还未见发表.

根据摩擦现象能否用微分方程表示，可以将摩擦力模型分为静摩擦力模型和动摩擦力模型[10].静摩擦力模型将摩擦力描述为速度的函数，模型结构较为简单、参数易辨识；动摩擦力模型将摩擦力描述为位移和速度的函数，模型更精确，但参数不容易辨识，动摩擦力模型在一定条件下可以转为静摩擦力模型.

近年来对弓网摩擦力建模也进行了相关研究，并取得了一定成果[11-12].本文通过分析摩擦力与压力波动频率、压力波动幅度、接触电流和滑动速度的关系，建立起弓网的LuGre 静态模型；在已经建立的静态摩擦的基础上，通过引入动态参数，建立了摩擦力的LuGre 动态模型，最后通过实验数据对两模型进行验证，以验证模型的有效性.

1 LuGre 模型

LuGre 模型是Canudas 等人于1995 年在Dahl模型和Bristle 模型的基础上提出的，该模型能够很好地解释爬行运动、Stribeck 效应及摩擦记忆特性等，是摩擦力研究中最著名的模型，LuGre 模型利用一阶微分方程刻画各种摩擦现象，可以实现在不同的摩擦状态下平滑的过渡，得到广泛应用[13-14]，但该模型的参数识别较为困难，特别是鬃毛刚度系数σ0和鬃毛阻尼系数σ1的辨识[15].该模型中物体表面接触示意，见图1.

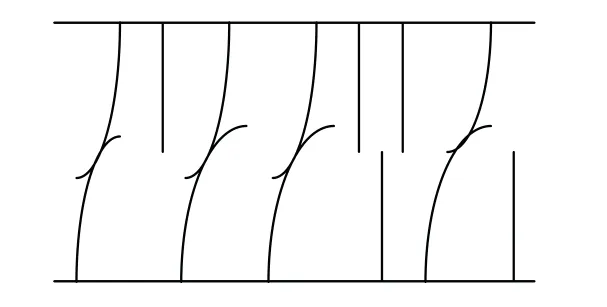
图1 LuGre 模型中物体表面接触示意Fig.1 surface contact in LuGre model

文献[11]基于Stribeck 效应建立了弓网的摩擦力模型，具有较高的精确度.LuGre 模型中包含了Stribeck 效应，比后者更加完善，为此，本文基于LuGre 模型建立起描述波动载荷下受电弓和接触网动态摩擦力方程，LuGre 模型的数学表达式为

式中，f为摩擦力，N；x˙为滑动速度，km/h；σ2为摩擦中的粘性摩擦系数；状态变量z为鬃毛平均变形量，m；z˙为状态变量z对时间的一阶导数，m/s；g(x˙) 描述的为Stribeck 效应，vs为Stribeck 效应参数；Fc、Fs分别为库伦摩擦力、最大静摩擦力，N；δ为经验参数，当δ=1 时为Tustin 模型，当δ=2时为Gauss 指数模型.

当鬃毛的平均变形量稳定时有z˙=0，则上式变为

该方程式（2）即为静态情况下的LuGre 模型.因此，本文思路为首先建立起弓网的LuGre 静态模型，对其参数进行辨识，再建立LuGre 动态模型，并对其动态参数进行辨识.

2 实验装置和实验方案

2.1 实验装置

实验采用载流摩擦磨损实验机，见图2.实验机可以模拟电力机车弓网系统接触导线和受电弓滑板之间的“之”字形运动轨迹.滑板和接触网导线之间的滑动速度可调范围为0～160 km/h；所加载的电流最大为800 A；压力波动频率的调节范围为0～20 Hz；实验中正弦形的波动压力是通过控制音圈电机来产生的[16].该实验机配备的NI PCI-6251 型数据采集卡可以实现对接触电流、滑动速度、摩擦系数、加速度等数据的实时采集并传到上位机的处理系统中显示与储存，以便进行后期分析处理.

图2 滑动电接触实验机Fig.2 sliding electrical contact experimental machine

实验中用到的接触导线为铜，截面积为120 mm2，其性能见表1.滑板为浸金属碳滑板，化学成份见表2.

表1 铜导线性能参数Tab.1 performance parameters of copper wire

表2 滑板材料化学成分Tab.2 chemical composition of slide material

2.2 实验条件

根据对弓网滑动电接触的相关研究[17-18]，结合以往关于最优压力载荷的研究成果[19]，将本实验的基准接触压力设定为70 N；对于铁路接触网，目前中国采用较多的是链型悬挂式，根据文献[20]的相关研究，Re250 DR-0 简单链型接触网固有频率为0.926 3～3.922 4 Hz，故将压力波动频率设定为1 Hz、2 Hz、3 Hz、4 Hz；根据文献[21]相关研究，目前普通客运、货运列车电流强度一般不大于300 A，速度一般不大于160 km/h，故将接触电流分别设定为100 A、150 A、200 A、250 A，将滑动速度分别设置为60 km/h、80 km/h、100 km/h、120 km/h.根据文献[22]，99.7%的接触压力数据分布在（Fm-3s）N 至（Fm+3s）N，其中Fm为平均值，s为标准差.根据文献[23]的相关研究，当速度为150 km/h 时接触压力标准差s为14.23 N，即波动范围未超过[-43 N 43 N]，故将接触压力波动幅度分别设定为[-10N 10 N]、[-20 N 20 N]、[-30 N 30 N]、[-40 N 40 N].实验采用控制变量法，通过控制压力波动幅度、压力波动频率、接触电流和滑动速度来测量摩擦力，每组实验做4 次，取其平均值.实验条件见表3.

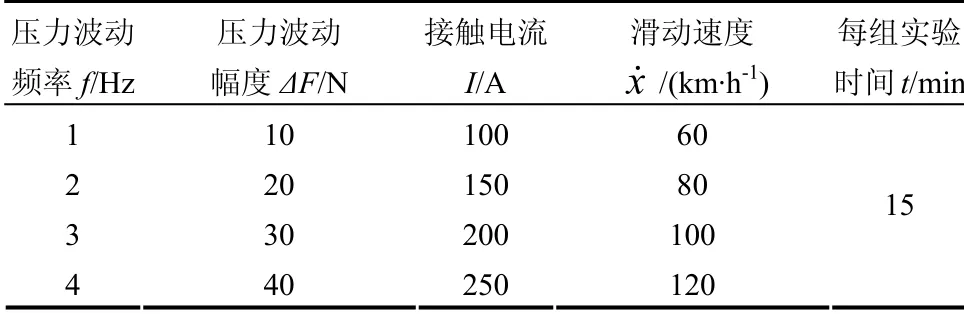
表3 实验条件Tab.3 experimental condition

3 LuGre 静态模型

3.1 LuGre 静态模型

稳态运行时，鬃毛平均变形量为零，即z˙=0，同时考虑粘性阻尼项影响[24]，故对式（2）修正为

式中，FN为正压力，N；μc为库伦摩擦系数；μs为最大静摩擦系数；σ为粘性效应.

3.2 LuGre 静态模型的改进

实际列车的运行情况非常复杂，所以需要对其进行修正，其中包括波动频率、接触电流、波动幅度、滑动速度等因素，现分别针对这些因素进行研究.

（1）反映压力波动频率和幅度的摩擦模型

在F=70 N，I=150 A，x˙=100 km/h，不同的压力波动幅度的条件下进行摩擦力和压力波动频率关系的实验，实验结果见图3.

图3 不同压力波动幅度下摩擦力随压力波动频率变化Fig.3 friction with fluctuation frequency under different fluctuation amplitude

由图3 可知，在压力波动幅度、接触电流、滑动速度一定的条件下，滑动摩擦力随压力波动频率的变化发生微小变化，平均值几乎不变，因此在该摩擦力模型中不需考虑波动频率变化的影响.

利用上述实验数据，同时可以得出相同频率下摩擦力随压力波动幅度的变化曲线，见图4.

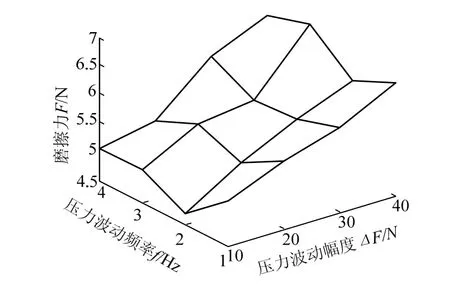
图4 不同压力波动频率下摩擦力随压力波动幅度变化Fig.4 friction with fluctuation amplitude under different fluctuation frequency

由图4 可知，摩擦力随压力波动幅度增大而增大，且两者近似成线性关系.

在基准压力FN一定时，实验中不同的压力波动幅度可表示成F1=FN±K·ΔF，即不同压力波动幅度会直接影响实际接触压力，故对式（4）修正为

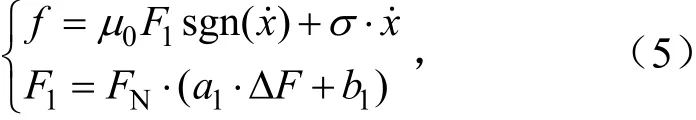
式中，a1、b1为这个模型中描述摩擦力随压力波动幅度变化参数.

（2）反映接触电流的摩擦模型

在F=70 N，f=2 Hz，x˙=100 km/h，不同的压力波动幅度的条件下进行摩擦力和接触电流关系的实验，见图5.

图5 不同压力波动幅度下摩擦力随接触电流变化Fig.5 friction with Contact current under different Pressure fluctuation amplitude

由图5 可知，摩擦力随接触电流增大而逐渐减小，且两者也近似成线性关系.

在压力波动幅度不变的情况下，通过改变接触电流的大小并不直接影响接触压力.当电流增加时，接触区域温度升高，鬃毛软化，接触点剪切抗力降低；同时高温会导致具有润滑作用的氧化物产生，两者共同作用导致摩擦系数降低，即接触电流会直接影响摩擦系数.故对（5）式作如下修正

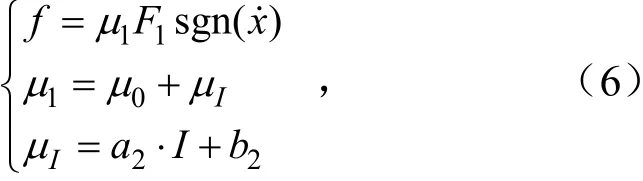
式中，a2、b2是这个模型中描述摩擦系数随接触电流的变化参数.

（3）反映滑动速度的摩擦模型

在F=70 N，f=2 Hz，I=150 A，不同的压力波动幅度的条件下进行摩擦力和滑动速度关系的实验，见图6.

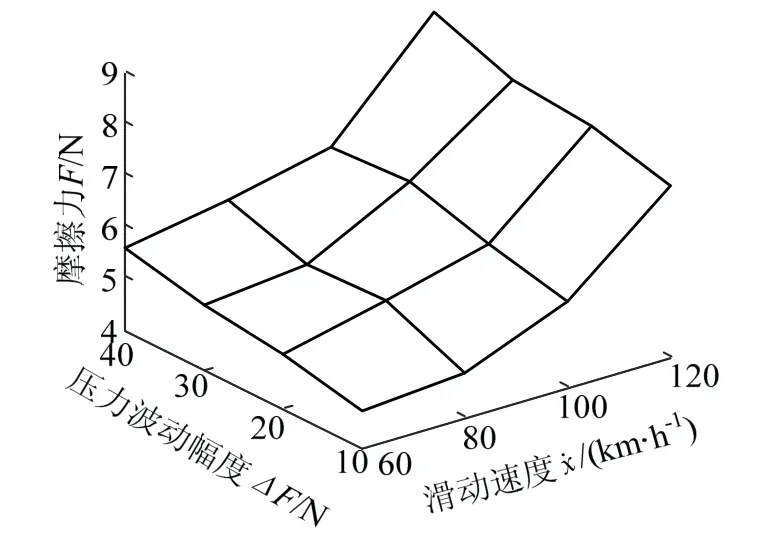
图6 不同压力波动幅度下摩擦力随滑动速度变化Fig.6 friction with sliding speeds under different fluctuation frequency

由图6 可知，摩擦力随滑动速度增大而增大，且随着滑动速度的增大，在相同速度增幅的条件下，摩擦力的增量逐渐增大，两者表现出明显的非线性关系.

在压力波动幅度不变的情况下，通过改变滑动速度的大小不会直接影响实际接触压力.在电流一定的情况下，滑动速度较低时，滑板和导线之间的接触状况良好，电弧放电现象不明显；随着滑动速度的提高，滑板和导线接触状况逐渐变差，导致产生电弧，由于电弧的烧蚀作用，滑板表面凹凸不平，从而导致摩擦系数的增大，即滑动速度会直接影响摩擦系数.故对式（6）修正为

式中，a3、b3、c3为这个模型中描述摩擦系数随滑动速度的变化参数.结合图6 中摩擦力随滑动速度的变化的趋势与Tustin 模型最为接近，故本文经验参数δ取1.

3.3 LuGre 静态模型

综上所述，在不考虑摩擦力方向的前提下，可建立静态摩擦力模型为

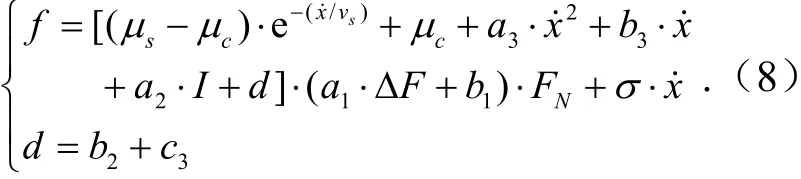
3.4 LuGre 静态模型参数辨识

国内外众多非线性拟合软件中，1stOpt[25]因其对初始值的要求低，且简单易学，寻优能力强，本模型中的未知参数采用该软件中的麦夸特法加通用全局优化法进行辨识.

根据前面分析，设定压力波动幅度、滑动速度、接触电流为已知变量，摩擦力为未知变量，选取图4、图5、图6 共48 组数据，利用曲线拟合软件1stOpt对式（8）中的未知参数进行辨识，并对模型进行评估，见表4、表5.

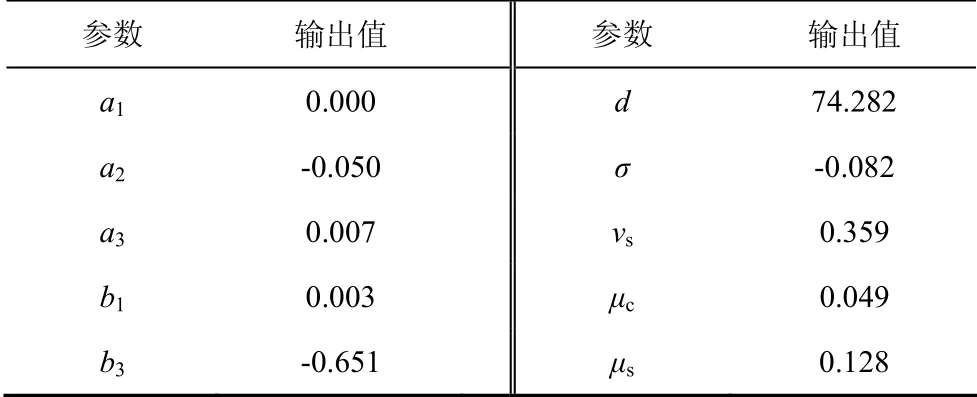
表4 模型参数值Tab.4 parameters’ value in model

表5 回归统计计量Tab.5 regression statistics

根据表5 可知，在一定误差内，所建立的模型拟合程度高、效果好，可以很好地反映出摩擦力随各种因素的变化规律.

4 LuGre 动态模型

4.1 LuGre 动态模型的改进

根据前面的分析可知，本文建模的过程是在稳态运行的条件下，根据实验结果，不断对摩擦力方程进行修正，从而建立出LuGre 静态模型.上述建模过程为不断对LuGre 模型中g(x˙) 做修正的过程，即

4.2 LuGre 动态模型参数辨识

LuGre 模型中的参数分为静态参数和动态参数，其中静态参数包括Fc、Fs、vs、σ2，动态参数包括σ0、σ1.其中Fc、Fs、vs已经在静态模型中完成辨识，只需辨识σ0、σ1、σ2.

为准确辨识模型参数，本文首先设定一组初始参数，对建立的Lugre 动态模型进行摩擦力仿真，通过与实测值对比，完成动态参数的辨识.

在众多算法中，遗传算法具有较高的准确度和速度，同时不像其他算法容易陷入局部最优，是一种优化算法，因此，这里采用遗传算法对Lugre 参数进行辨识，LuGre 模型动态参数辨识流程见图7.

图7 动态参数辨识流程Fig.7 flow for dynamic parameters identification

设实验摩擦力为f1，通过在Simulink 中构建LuGre 模型仿真图，并生成摩擦力f2，则摩擦力误差可表示为

遗传算法的目标函数为

辨识的目的即为求取上式的极小值，从而辨识出相应的模型参数，具体步骤如下.

步骤1设定初始参数：F=70 N，f=2 Hz，I=150 A，=100 km/h，σ0=1 715 N·m/s，σ1=0.073 N·m/s，σ2=0.001 N/m，其余参数取自表4.

步骤2动态模型仿真：将上述实验条件代入动态模型仿真程序中进行摩擦力仿真，仿真输出值为f2(i) .

步骤3仿真结果对比：将5 000 组实测摩擦力f1(i) 和5000 组仿真输出值f2(i) 进行误差对比.

步骤4完成动态参数辨识：从Matlab 工具箱中调用遗传算法程序包（GA），编写程序，设定参数上下限，求取目标函数极小值，辨识未知参数.

通过遗传算法辨识出的未知参数见表6.

表6 模型参数值Tab.6 parameters’ value in model

至此，模型中的静态参数和动态参数全部辨识出来了，还需要对模型进行验证与评估.

5 模型的验证与分析

5.1 模型的验证

LuGre 模型优势是善于捕捉滑动速度变化时摩擦力的变化，为了验证所建立模型的准确性，额外测量一部分数据，给出速度变化时模型的验证结果，并对其进行评价.在F=70 N，f=2 Hz，ΔF=20 N，I等于100 A、150 A、200 A、250 A，x˙等于70 km/h、90 km/h、110 km/h、130 km/h 的条件下，测出实际的摩擦力，分别将上述条件代入纯机械的LuGre 模型和所建立的两个模型中，得到相应的摩擦力输出值，以便进行比较从而验证模型的有效性，并对两模型进行分析与评估.摩擦力随滑动速度变化曲线见图8.

图8 不同接触电流下摩擦力随滑动速度变化Fig.8 variation of friction with sliding speed under different contact current

根据图8 可知，纯机械的LuGre 模型的误差随着接触电流的增加而增大，当接触电流为100 A 时，其最大相对误差为19.230%，当接触电流为250 A时，其最大相对误差为32.002%，故本文建立的摩擦力模型较纯机械的LuGre 模型更具有有效性.通过计算有：静态模型的最大相对误差为10.851%，最小相对误差为2.503%，平均相对误差为4.038%；动态模型最大相对误差为8.874%，最小相对误差为0.562%，平均相对误差为2.365%.因此，本文所建立的LuGre 摩擦力模型，无论是静态模型还是动态模型都能很好的模拟实际摩擦力的变化情况，且动态模型较静态模型更加精确，输出值更加接近实际摩擦力.动态和静态摩擦力模型误差对比见图9.

图9 动态和静态摩擦力模型误差对比Fig.9 error comparison chart of dynamic and static friction model

通过图9 可知，16 组验证实验中，动态模型误差较静态模型误差小的占12 组，其中静态模型的均方差为5.253%，动态模型的均方差为4.949%，动态模型更具有有效性.

5.2 动态模型的优异性分析

通过以上分析可知，动态模型较静态模型更为精确、有效，两者之间的区别是动态模型引入了刚度系数σ0和阻尼系数σ1.

列车在运行过程中，由于运行速度、接触电流、接触压力不断变化等原因，滑板在切向和法向上都有变形，滑板上鬃毛的平均变形量不再趋于稳定，即不再满足z˙=0，而静态模型不能很好地描述这部分变化.滑板和导线之间的接触，实际上是通过两者表面无数细小的鬃毛接触，接触时两者表面的鬃毛发生弹性或塑性形变，滑板和导线之间相互滑动的过程，在微观层面上两者表面的鬃毛不断摩擦，进而软化、脱落，且波动压力越大、接触电流越大、滑动速度越快这种现象越明显，温度也越高，鬃毛的刚度发生变化，这一变化通过刚度系数σ0来描述；随着滑动速度的改变，鬃毛在发生软化的同时，鬃毛之间的粘滞现象不能忽略，且速度越大，粘滞现象越明显，这一现象通过微观阻尼系数σ1来描述.动态模型综合考虑了刚度系数σ0和阻尼系数σ1的影响，模型更加全面，更接近实际情况，因而其更加精确，更具有有效性.

在本文实验条件的范围内,当滑板和接触导线材料均不变时，所建立的模型可直接使用，且具有较高的精确度；当滑板和接触导线材料改变时，考虑到不同材料会有不同的摩擦系数、刚度系数、阻尼系数等，需要对模型中的μc、μs、vs、σ0、σ1、σ2等参数进行修正，但模型的结构形式不变.

6 结论

（1）通过研究静态情况下摩擦力与压力波动幅度、接触电流、滑动速度的关系，通过修正已有的LuGre 模型，建立LuGre 静态摩擦模型；在已经建立的静态摩擦的基础上，通过引入动态参数，建立了摩擦力的LuGre 动态模型，动态模型具有更高的精确度，输出值更加接近实际摩擦力.

（2）在建立模型的过程中未能全面考虑实际运行中噪声、温度变化、振动等随机干扰因素，今后会针对这些问题再进行相关的研究，建立更加精确的模型.

（3）建立的LuGre 动摩擦模型，将动摩擦模型引入到弓网滑动电接触领域，为弓网滑动电接触在摩擦动力学方面的研究奠定了基础.