电压源型三相逆变器的模型预测控制策略

张薇琳，陈灵敏

（1.广东交通职业技术学院轨道交通学院，广东 广州 510650；2.广东工业大学试验教学部，广东 广州 510006）

三相逆变器是电力电子与电力驱动领域中最重要、最经典的研究对象之一[1-3]，其中，电流控制在过去几十年中已经深入研究，如传统的滞环电流控制器和基于比例积分（proportional inte⁃gral，PI）的调节器和脉宽调制（pulse width modu⁃lation，PWM）的控制器等[4-5]。

随着微处理器的快速发展，其运算能力显著增强，进而模型预测控制（MPC）也得到了更多的关注[6-13]。MPC控制器中，负载和变换器模型用于系统行为预测，从而可根据任意设定的控制指标选择最合适的输出[6]。预测控制是一个非常广泛的概念，包含了很多的控制方案，其中一个主要的类别为使用预测控制来计算所需的负载电压以优化电流行为，并使用调制器产生该期望电压。在该种方法中，变换器被简单地建模为增益，从而设计出电流控制器并应用于逆变器[7]，以及整流器[8]和有源滤波器[9]。MPC控制器的一大优点是可以在预测模型中包含系统的非线性因素，并据此计算不同开关状态下的系统行为。其中文献[10-11]利用该特性实现了最小化大功率逆变器的开关频率。而文献[12]则利用预测控制的这种特性评估四桥臂有源电力滤波器中每个开关状态的电流误差。文献[13]提出了一种用于矩阵变换器的MPC控制策略，控制器中系统模型用于预测矩阵变换器的每个不同开关状态下的负载和输入电流的行为，然后选择使成本函数最小化的开关状态，该种方案可避免使用复杂的调制技术。

基于前述文献研究基础，本文设计了一种新颖的MPC控制器用于电压源型三相逆变器。新控制器中成本函数设计为下一个采样周期的电流误差，然后基于三相逆变器系统的离散时间域模型来进行预测，并选择最小化成本函数的矢量作为最优矢量输出。最后进行了仿真和实验研究，与传统逆变器控制方案的对比测试结果验证了新型MPC控制器具有更优的控制效果。

1 传统控制方案

三相逆变器的传统控制方案主要包括滞环电流控制方案[4]和PWM的控制方案[5]。前者使用测量的电流和电流参考值进行滞环比较生成控制信号，故控制方案概念简单，动态性能较好。但各相之间没有完全解耦，且开关频率将根据负载参数和工况的变化而变化，易引起谐振问题，同时也限制了其应用于大功率逆变器。后者将输出电流参考值和实际电流值之差经PI调节器生成了负载电压参考值，送至PWM生成模块生成控制脉冲，故开关频率固定，而控制性能取决于控制器参数设计，同时输入的正弦参考误差易随参考电流的频率增大而增加，在某些应用场合可能无法接受。

2 MPC控制器设计

设计电压源型三相逆变器的MPC控制策略前，先假设：逆变器仅可生成有限数量的开关状态，并且系统模型可用于预测每个开关状态对应的变量行为。为了选择要施加的开关状态，必须定义控制性能相关指标，具体表现形式就是成本函数，然后基于成本函数评估每个开关状态并择取最优开关状态。

MPC控制器设计包含了以下步骤：1）定义成本函数；2）构建逆变器数学模型及其所有的开关状态；3）构建负载模型以进行预测。其中负载模型需为离散时间域模型，结合成本函数预测评估变量行为，即负载电流的行为。

图1为应用于电压源型三相逆变器的MPC控制策略框图。

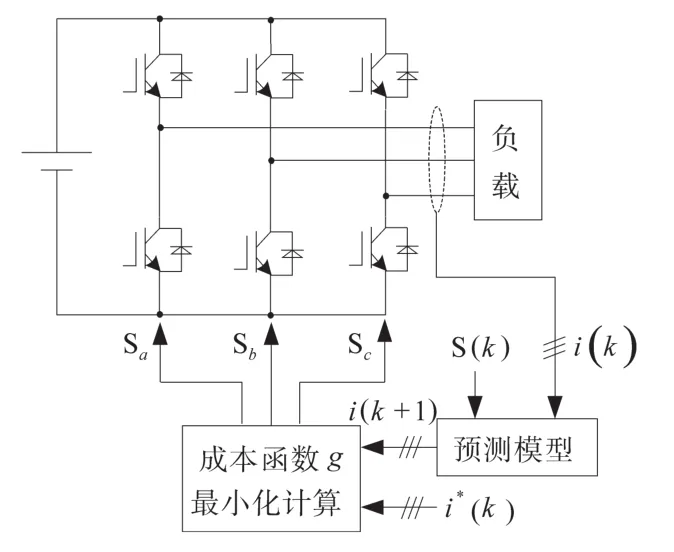
图1 新型MPC控制方案框图Fig.1 Block diagram of new MPC control scheme

如图1所示，控制器的执行包含以下步骤：1）获取参考电流的值，这来自外部控制回路，如转速外环、功率外环或电压外环，并测量实际的负载电流；2）基于系统模型预测每个不同电压矢量对应的下一个采样周期的负载电流值；3）基于成本函数评估下一个采样周期中参考电流值和预测电流值之间的误差。选择最小化电流误差的电压矢量进行应用。

2.1 成本函数设计

下一个采样周期的电流误差可在α-β坐标系中表示如下：

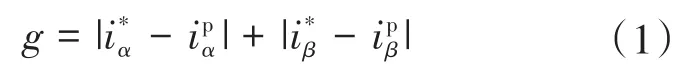
不同的控制性能相关指标将以不同的成本函数表示。例如本文使用的绝对误差具有计算简单的优点，此外还有误差采样周期积分或平方误差等。进一步结合外部控制环也可设计出贴合控制目标的成本函数，如电机驱动控制中转矩或转速误差、功率控制中有功或无功功率误差等。此外，还可以设计出改善其他系统性能的控制目标相关成本函数，如最小化开关频率等。

2.2 逆变器模型

图2为电压源型三相逆变器的电路图。

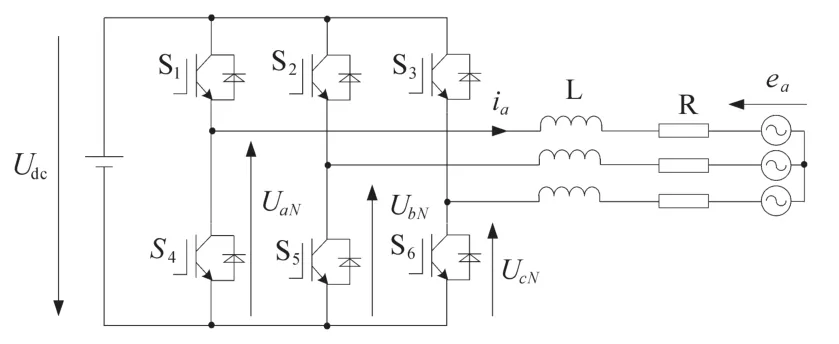
图2 电压源型三相逆变器的电路图Fig.2 Circuit diagram of voltage source three-phase inverter

逆变器的开关状态由驱动信号Sa，Sb和Sc决定：

可以表示为矢量形式如下：

进一步可得逆变器的输出电压空间矢量u为

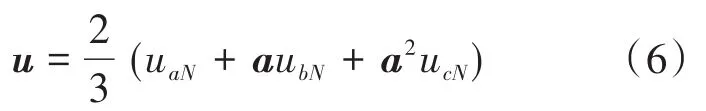
式中：vaN，vbN和vcN为逆变器的中性点电压。

矢量u和S的关系式为

式中：Udc为直流电压。

考虑到驱动信号Sa，Sb和Sc一共构成了8个开关状态，并由此获得了8个电压矢量，其中零矢量u0=u7，故有效电压矢量有7个，如图3所示。

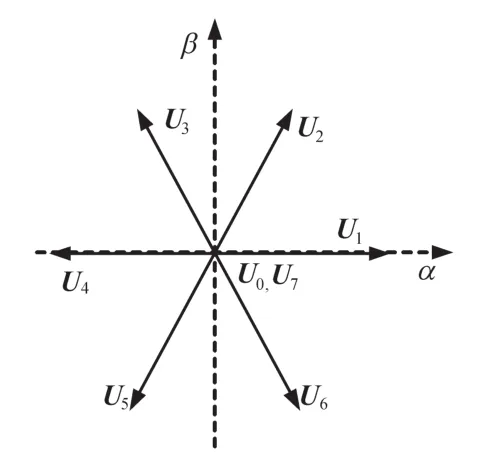
图3 有效电压矢量示意图Fig.3 The schematic of effective voltage vectors

当使用PWM等调制技术时，逆变器可建模为线性系统。然而，在本文中，逆变器被认为是一个非线性离散系统，并由7种不同的开关状态作为输出。更精确的逆变器模型可包括死区时间、IGBT饱和电压和二极管正向压降等因素。但增加的模型复杂度带来的控制精度增加有限，故采用一个较为简单的逆变器模型即可。

2.3 负载模型

三相平衡负载下的电流矢量可定义为

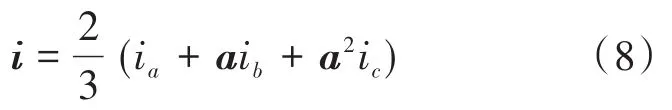
负载的反电动势可定义为

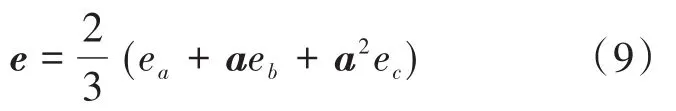
因此，负载电流动态可以通过以下矢量方程来描述：

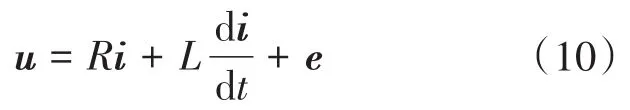
式中：R和L为负载电阻和负载电感；u为逆变器输出电压矢量；e为负载反电动势矢量；i为负载电流矢量。

后续仿真和实验中假设负载反电动势是具有恒定幅值和频率的正弦曲线。

2.4 离散时间域模型

基于采样周期Ts对式（10）进行了离散化处理后，即可用当前采样周期的电流、电压测量值来预测下一个采样周期的负载电流值。

负载电流微分可离散化如下：

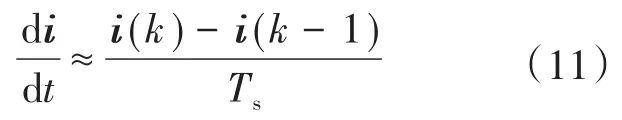
式中：k-1为前一个采样周期；k为当前采样周期。将式（11）代入式（10）可得：

进一步，将步长向前移动一步，即可以预测未来的负载电流值如下：

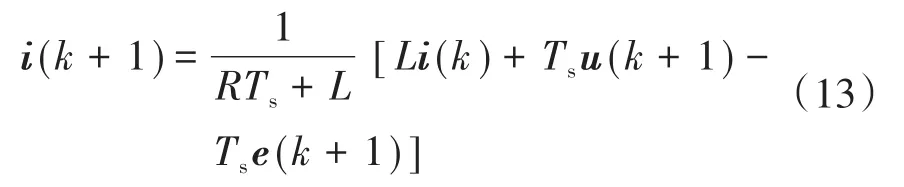
式中：k+1为下一个采样周期。

对于负载反电动势可以使用式（12）和测量的负载电压和负载电流来进行估计。ê(k)的估计e（k）如下式所示：

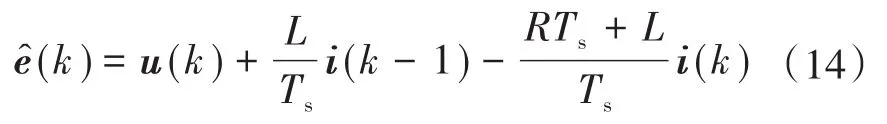
可以使用估计反电动势的当前采样周期值和上一个采样周期值外推下一个采样周期的反电动势，或者假设反电动势在一个采样间隔内无显著变化，即 e(k+1)=ê(k)。

2.5 电压矢量选择

在MPC算法中，对于7个不同的有效电压矢量，基于式（13）给出7个不同的电流预测值。而电流预测值最接近电流参考值的对应电压矢量将在下一个采样时刻进行实施。换言之，所选择的有效电压矢量将是使成本函数最小的电压矢量。

成本函数计算公式如下：

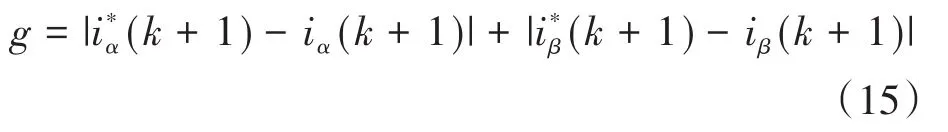
式（15）中下一个采样周期的电流参考值是未知的。因此，采用二阶外推从当前采样周期的电流参考值、上一个采样周期的电流参考值和更早一个采样周期的电流参考值来得到下一个采样周期的电流参考值如下：

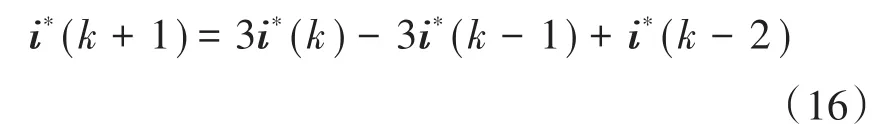
对于采样周期Ts足够小的情况，近似有i*（k+1）=i*（k），这在图3中有体现。

3 MPC控制器的实现

图4为将MPC控制算法在DSP中实现时的DSP不同任务执行时序图。图5为MPC控制器算法流程，其中，A为应用新的开关状态，B为电流测量，C为反电动势估计，D为负载电流预测和开关状态选择。

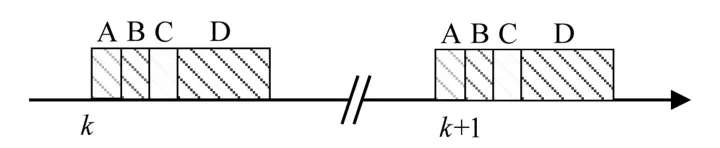
图4 任务时序图Fig.4 Diagram of task timing

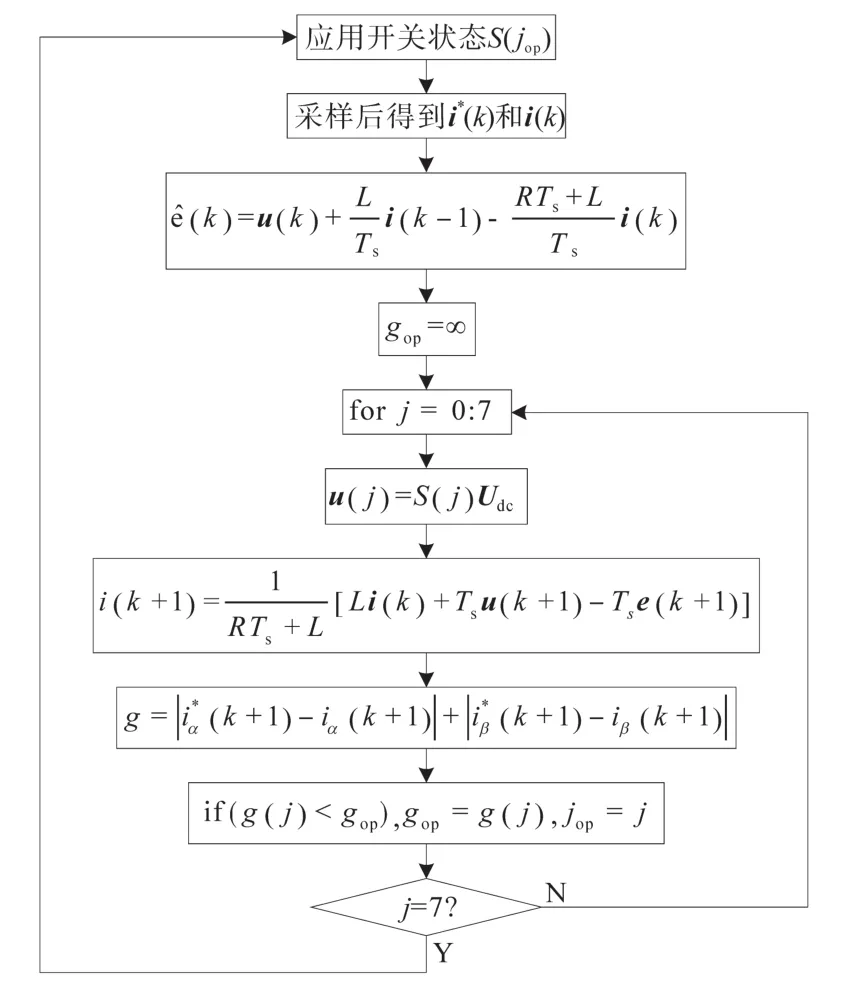
图5 算法流程图Fig.5 Flow chart of the algorithm

如图4所示，DSP的1个采样周期中需执行4个主要任务，4个主要任务的持续时间约为7 μs。其中最重要的计算任务是负载电流预测和新的开关状态选择。DSP的6个数字输出可用于直接提供IGBT驱动信号，而这些输出由控制算法直接设置，无需PWM调制器。同时，DSP的2个模拟输入可测量负载电流，得到负载电流的相位用于计算电流矢量。如图5所示，成本函数的最小化计算过程对所有开关状态进行了评估，并得到最优开关状态用于下一个采样周期实施。整个控制算法以非常简单的方式实施，故MPC控制器易于实现。

4 仿真分析

基于Matlab/Simulink仿真平台进行了三种不同的逆变器控制方案的仿真分析，并进行了仿真结果的对比。

系统中的反电动势为正弦波，具有固定的幅值和频率，直流电压Udc固定在100 V，负载电阻R为0.5 Ω，负载电感L为10 mH。为了方便对比，将PWM控制方案中载波频率设置为2 kHz，同时设置滞环电流控制方案的平均开关频率为2 kHz。

图6为MPC控制器的稳态仿真波形，从图中可以看出，负载电压的波形存在较大的基频分量和高次谐波分量。

图6 MPC控制器稳态仿真波形Fig.6 Steady-state simulation waves of the MPC controller

图7为采用传统滞环电流控制的仿真结果，如图7所示，该控制方案呈现出了较好的动态响应，但也存在明显的耦合效应。图8为采用传统的PWM控制方案的仿真结果，图8中显示耦合效应依然存在，同时动态响应也较慢。图9为新型MPC控制方案的仿真结果。对比图7和图8可看出，在相同的动态下，所提出的MPC控制器的动态响应与滞环控制获得的动态响应一样快，并实现了两个电流分量之间的解耦。

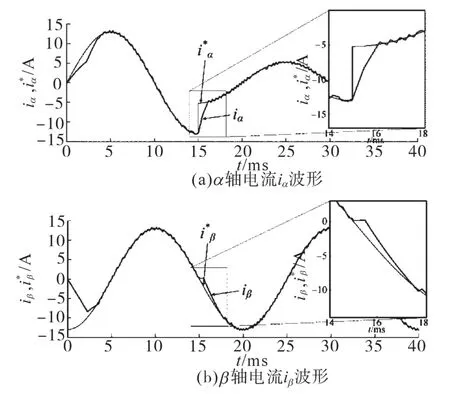
图7 滞环电流控制器动态仿真波形Fig.7 Dynamic-state simulation waves of the hysteresis current controller

图8 PWM控制器动态仿真波形Fig.8 Dynamic-state simulation waves of the PWM controller

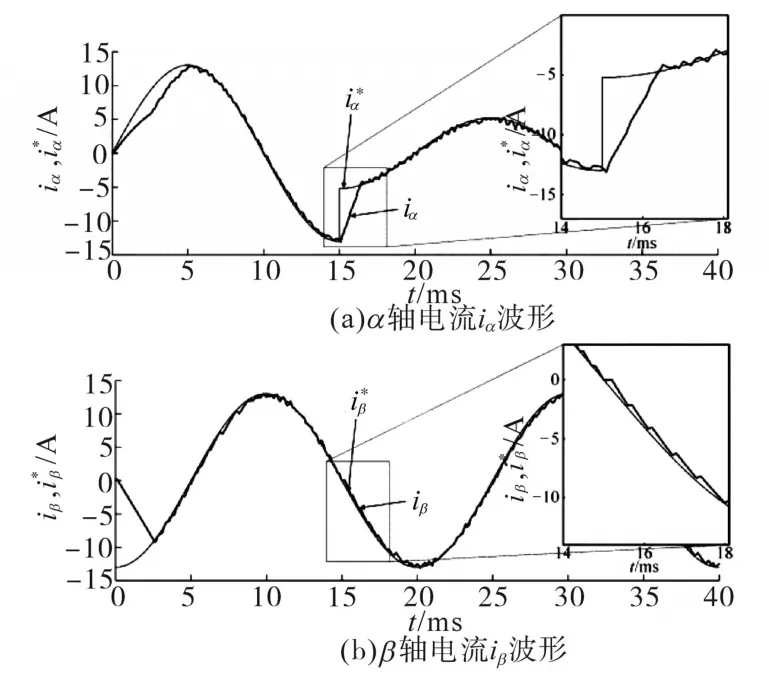
图9 MPC控制器动态仿真波形Fig.9 Dynamic-state simulation waves of the MPC controller

对于逆变器控制而言，除了控制电流跟踪参考值外，还有一个重要的性能指标是逆变器输出电压的电能质量，主要是就是频谱，故仿真计算了三种控制方法的输出电压频谱，仿真分析结果如图10所示。

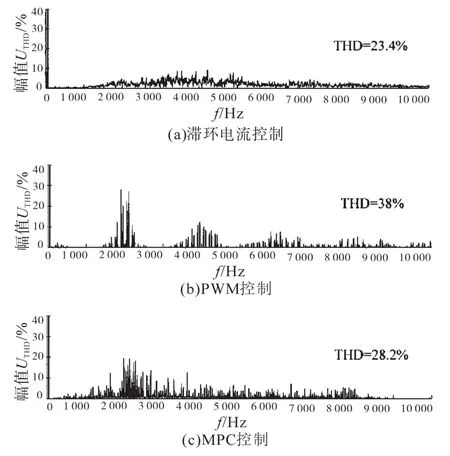
图10 3种控制方法的输出电压频谱分析Fig.10 Analysis of the output voltage spectrum with three control methods

图10a为滞环电流控制下的输出电压频谱，其是分散状，这不利于以后的优化，而10b为PWM控制下的输出电压频谱，其主要集中在开关频率及其倍频附近，这是有利于后期滤波优化的，图10c为新型MPC控制器作用下的输出电压频谱，对比图10a和图10b可看出，频谱类似于PWM控制下的频谱，故也是有利于后期优化的。

5 实验验证

为了测试所设计的电压源型三相逆变器MPC控制方案，搭建了逆变器样机实验平台。实验中将TI公司的DSP芯片TMS320F28335作为控制算法实现的主体。逆变器主体由三菱公司的智能IPM模块实现，逆变器前端由不控整流器供电，逆变器输出直接接入到有源阻感负载，采用传感器测量逆变器输出电流，同时DSP直接产生IGBT的门极驱动信号。开展了两组实验，采样周期 Ts设置为 100 μs，额定频率 fn为 50 Hz，直流电压Udc固定为100 V，负载电阻R为10 Ω，负载电感L为12 mH，反电动势为正弦波，具有34 V的固定幅值和50 Hz的固定频率。为了简化运算过程，对式（13）进行了简化，忽略了电阻R的影响，从而有：

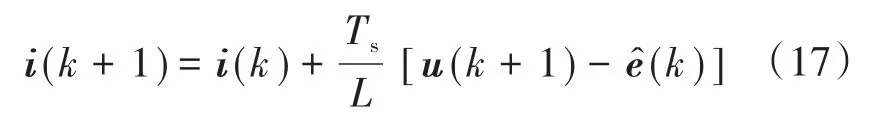
图11为α轴参考电流阶跃变化动态测试结果。

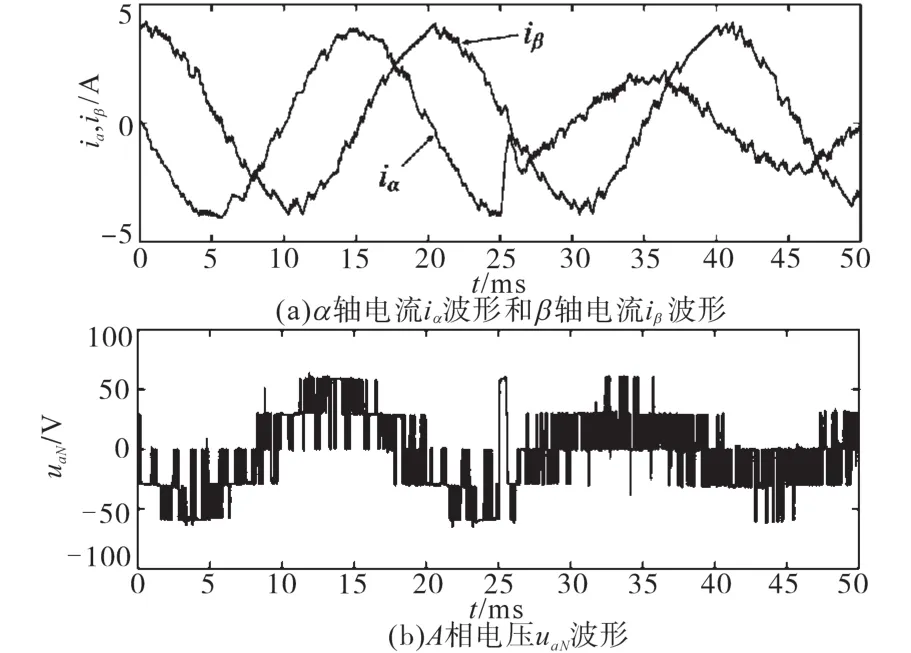
图11 α轴参考电流阶跃变化动态测试结果Fig.11 Dynamic test results of α-axis reference current step change

图11a为t=25 ms将α轴参考电流i*α从4 A阶跃变化至2 A的动态实验结果。由图11a中可看出，系统表现出了快速的电流动态响应，并和前述图9的仿真结果吻合。图11b为对应的负载电压波形。由图11b可知，IGBT的驱动信号可以直接由MPC控制器生成，而无需PWM调制器。

图12为设置电流参考值为方波时的电流动态性能测试结果，测试结果显示电流能准确地跟踪参考值。

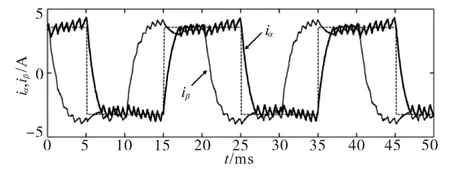
图12 参考电流方波变化动态测试结果Fig.12 Dynamic test results of reference currents square wave variation

图13为A相电压uaN的频谱，对比图10c可知，实验中得到的电压频谱规律和仿真是对应的。

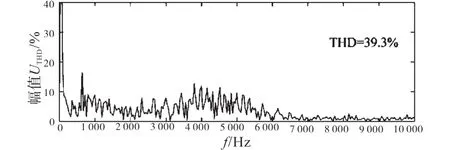
图13 实验中输出电压频谱分析Fig.13 Analysis of the output voltage spectrum in the experiment

6 结论

为提高电压源型三相逆变器的控制性能，设计了新型的MPC控制器，通过与传统滞环电流控制和PWM控制对比分析，以及仿真和实验研究，可总结结论如下：

1）基于逆变器和负载的数学模型，离散化后可进行变量预测，将开关状态代入所设计的成本函数，可直接输出最优驱动脉冲，而无需调制器；

2）对比传统控制策略，新方案充分发挥了逆变器和数学芯片的离散特性，具有更优的电流控制动态性能，且易于实现；

3）进一步的研究方向是针对不同应用场合，改进成本函数可设计出不同控制目标的模型预测控制器。