基于扰动转矩观测器PMSM无位置传感器控制系统

阴建强，邬贤明，邬冯值，杨沛豪

（1.郑州电子信息中等专业学校电子信息部，河南郑州450100；2.宁波广播电视集团，浙江宁波315000；3.足利大学信息科学与制造工程学院，日本枥木326-0845；4.西安热工研究院有限公司，陕西西安710054）

PMSM因为其带载能力强，在工业上，尤其是机车牵引、绞车提升等矿业工作中，得到了大规模应用[1-2]。为了实现PMSM换相，需要利用霍耳位置传感器或其它位置检测装置来实时检测转子位置。为了节约体积、节省成本，采用算法实现电机换相成为最近电机控制领域研究的热点[3-4]。

目前针对PMSM无位置传感器控制算法主要有：龙伯格控制算法[5]、卡尔曼控制算法[6]、滑模控制算法[7]、定子磁链估计器算法[8]等。定子磁链估计器算法是一种基于电压模型的定子磁链估计器，这种估计器是根据反电动势来构造的，低速时存在反电动势低、信噪比低等问题，无法实现低速正常工作。

为了提高PMSM无位置传感器低速控制性能，文献[9]提出一种基于电流模型的定子磁链估计器，但是该估计器依赖于转子位置信息，无法实现全转速范围无传感器控制。文献[10]采用高频信号注入法提取电机转子位置信息，但是一般控制系统中没有单独设置电流、电压环，高频电压、电流信号难以控制，很大程度上影响了控制精度。

针对PMSM运行过程中，控制系统易受转矩脉动的影响，文献[11]对电机驱动电路元器件的开断及死区引起的转矩脉动进行抑制，但因为采样时机不确定导致易出现假脉冲，无法实现精确脉动抑制。文献[12]提出一种不确定干扰估计控制模型，该控制模型由一阶滤波器构成不受建模不准确性的影响，但存在参数调整较为复杂的问题。

本文提出一种基于低速脉冲高频定子磁链注入的PMSM无位置传感器控制系统，通过向定子磁链幅值注入高频信号，在三相绕组中产生高频电流，高频电流被发送到转子位置和转速估计器，实现无位置传感器控制。对定子磁链估计器进行改进，将高频信号引入低通滤波器中以提高电机低转速运行时定子磁链估计器的精度。针对PMSM中低速运行时，无位置传感器控制系统易受转矩脉动影响的情况，本文采用扰动转矩观测器来抑制扰动转矩产生的电压误差，通过构造一个准微分形式的观测器，抑制微分环节对误差信号放大作用。最后通过试验验证所提方案的有效性和可行性。

1 PMSM数学模型

为了建立PMSM数学模型，定义d，q轴、α，β轴坐标系，其中d，q轴是转子磁场定向坐标系，α，β轴是定子静态坐标系，坐标定义如图1所示。

图1 坐标定义图Fig.1 Coordinate definition diagram

图1中：θe为转子旋转电角度；ωe为转子旋转电角速度，即定子电流旋转角频率；us，is，Ψs，Ψr分别为定子电压矢量、定子电流矢量、定子磁链矢量和转子磁链矢量；上标“ˆ”代表估计值。PMSM在d-q旋转坐标系下的数学模型为

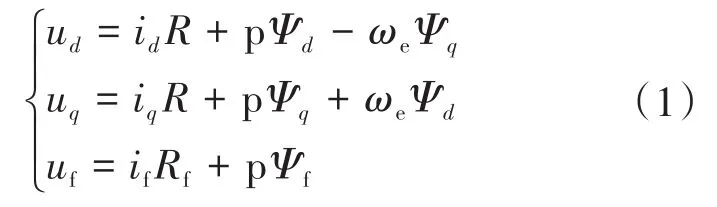
式中：id，iq，ud，uq分别为d，q轴电流、电压；R为定子电阻；Ψd，Ψq分别为d，q轴定子绕组磁链；uf，if，Rf分别为转子电压、电流、电阻；Ψf为永磁直轴磁链；p为微分算子。

通过在定子磁链中注入高频信号来计算PMSM转子位置、定子磁通幅值和电磁转矩为

当把高频信号注入到定子磁链后，在PMSM绕组内会产生高频定子电压电流分量。参考式（1），高频定子电压为

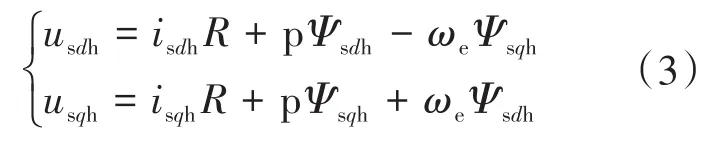
式中：usdh，usqh，isdh，isqh分别为d，q轴下定子电压、定子电流的高频分量；Ψsdh，Ψsqh分别为d，q轴下定子绕组磁链高频分量。

忽略定子压降，并且PMSM中低速运行时，定子高频电压信号旋转角频率ωh远大于定子电流旋转角频率ωe，因此可忽略掉表达式中的反电动势项和交叉耦合项对高频定子电压数学表达式的影响，式（3）可转换为

2 改进定子磁链估计器

2.1 估计器构造

定义实际转子同步坐标系和估计转子同步坐标系转换变量为

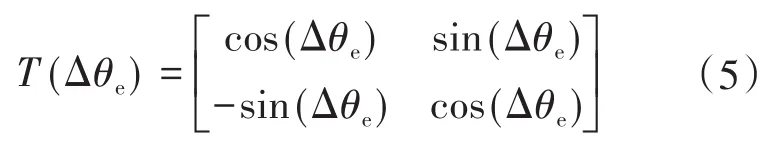
式中：Δθe为估计误差。

转子同步坐标系下的定子磁链和电流估计值为

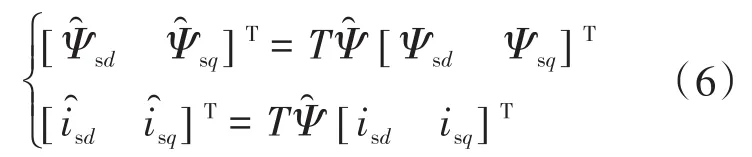
估计转子同步坐标系中，定子磁链振幅表示为

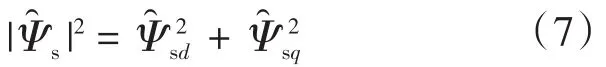
将式（6）中关于定子磁链的表达式代入式（7）中，可得：

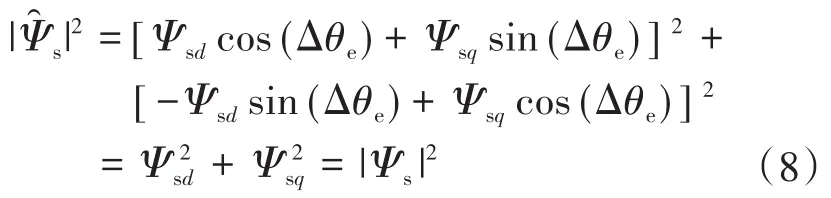
根据式（6），可以推导出转子同步坐标系下的电磁转矩为

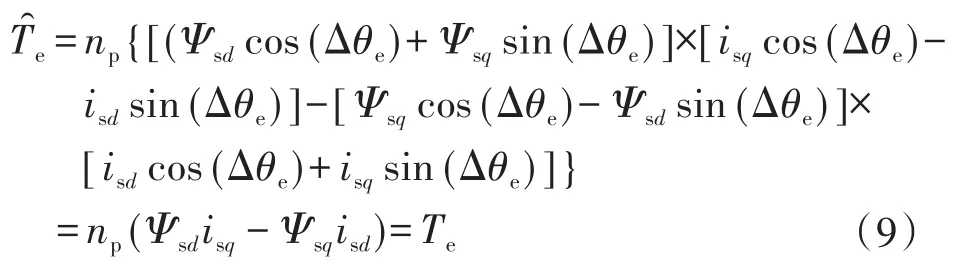
根据式（8）、式（9）可以得出：定子磁链振幅和电磁转矩估计值等于实际值，这为实现PMSM低速无位置传感器控制提供了良好的条件。

PMSM的d，q轴特性几乎相同，满足Ld=Lq，当采用id=0控制时，根据式（2）电磁转矩表达式，可以得到电磁转矩与定子磁链幅值之间关系[13]：

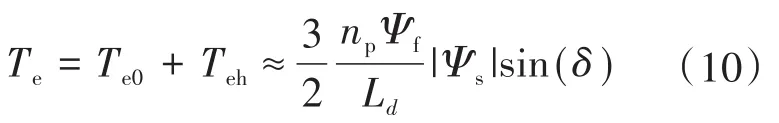
式中：np，Ψf，Ld为电机物理参数。

电磁转矩的高频分量由|Ψs|sin(δ)产生，由于电气常数远远小于转子机械常数，在一个采样周期内，认为电磁转矩Te保持不变，电磁转矩的高频分量可近似为0，可表示为

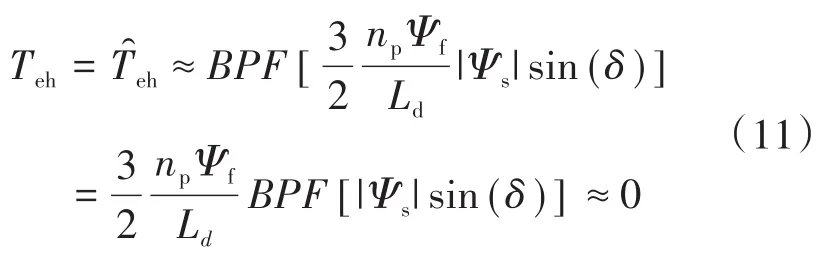
式中：BPF代表带通滤波器。

因为npΨf/Ld≠0，所以BPF|Ψs|sin(δ)≈ 0，sin(δ)≈ 0，cos(δ)≈ 1。经过带通滤波器的定子磁链幅值为

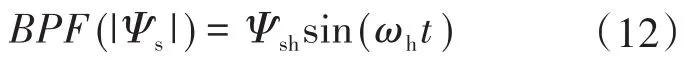
式中：Ψsh为高频分量电角频率。

定子磁链幅值也可表示为

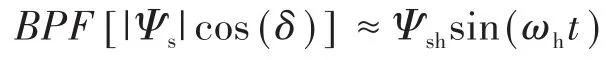
在实际的转子同步坐标系中，高频定子电流为

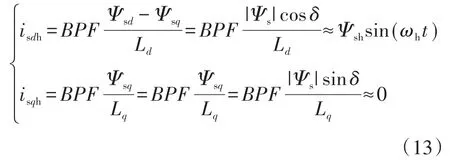
将式（13）代入式（6）中，估计d-q坐标系下高频定子电流为

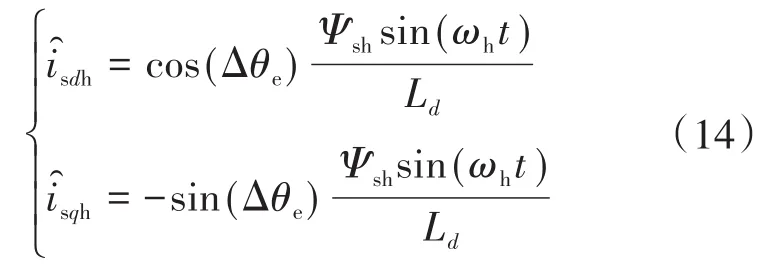
根据式（14），可以得出d，q轴定子电流为

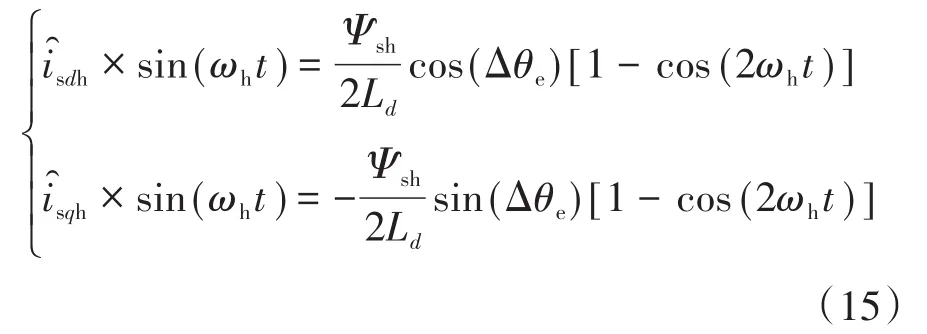
2.2 低通滤波器及磁极判据

本文采用低通滤波器对高频定子电流进行信号过滤。经过低通滤波器得到的定子电流q轴高频分量，当θe的值较小时，可表示为

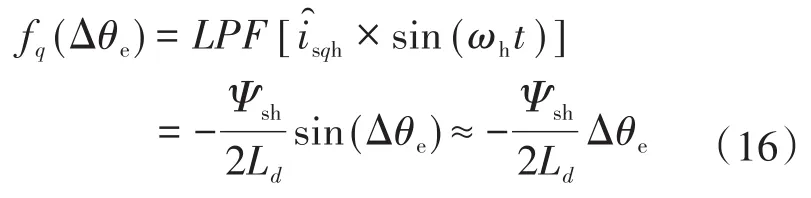
式中：LPF代表低通滤波器。

如果式（16）中的信号为零，则Δθe将等于零。因此，估计的转子位置将等于实际转子位置。

转子位置可以准确估算，但存在磁极无法判断的问题，估计转子位置可以等于实际值，或者与实际相差180°，因此磁极判断是必要的。让式（14）中的d轴电流信号通过低通滤波器，可以得出：

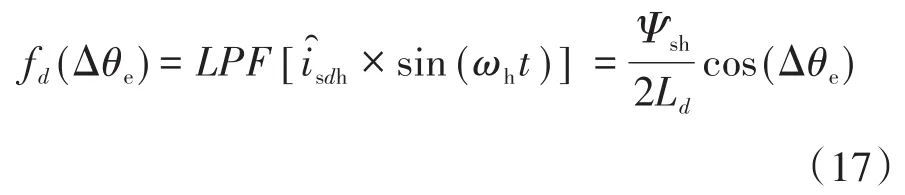
根据式（17），磁极判据如下：

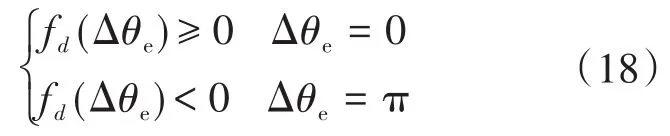
基于以上分析，建立PMSM转子位置和转速观测器，如图2所示，其中，d，q轴定子磁链通过带通滤波器，转换为高频定子电流，通过估计转子同步坐标系转换变量得到其估计值，高频定子电流估计值通过低通滤波器进行信号过滤，d轴高频分量信号进行磁极判据，q轴高频分量信号估计的转子位置。

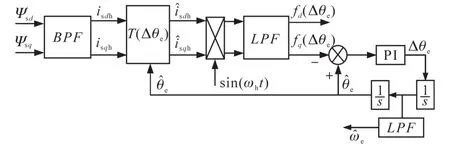
图2 转子位置和转速观测器Fig.2 Rotor position and speed observer

3 扰动转矩观测器

3.1 扰动转矩观测器构造

PMSM在d-q旋转坐标系负载转矩可表示为

式中：J为电机的转动惯量；ω为机械电角速度。

PMSM中低速运行时，无位置传感器控制易受转矩脉动的影响，本文采用扰动转矩观测器来实时估算干扰转矩所对应的电流补偿量，常规扰动转矩观测器表达式为

式中：KL为PMSM转矩常量。

扰动转矩观测器需要将iq作为输入，但iq大多含有噪声，需要经过滤波器滤除；常规扰动转矩观测器对扰动转矩进行计算时，需要引入微分环节，这无疑增大了观测误差，因此本文提出一种改进扰动转矩观测器：

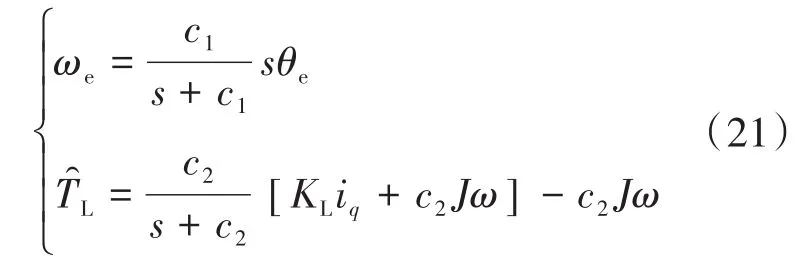
式中：c1，c2为观测器增益。

本文在扰动转矩观测器加入一阶低通滤波器来消除iq中的高频噪声和误差；为了提高响应速度，在扰动转矩估计时不进行微分运算，仅在转速计算时进行微分运算，进一步降低了观测误差。

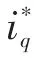
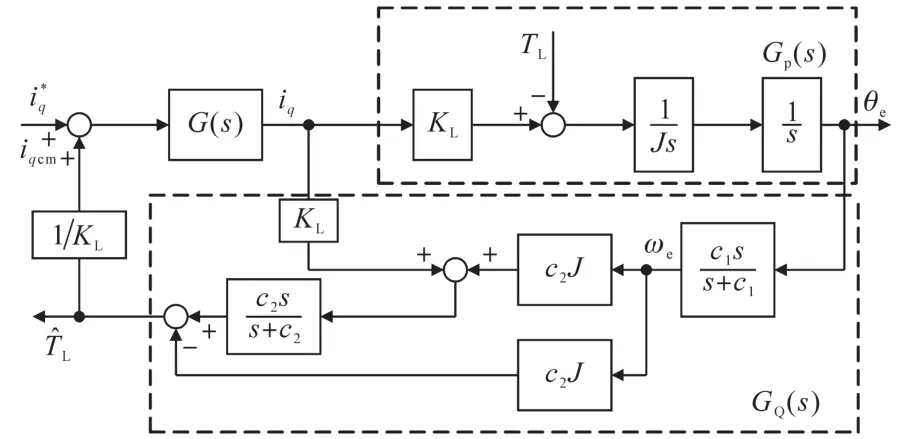
图3 扰动转矩观测器结构框图Fig.3 Structure block diagram of disturbance torque observer

3.2 扰动转矩观测器稳定性分析

当PMSM无位置传感器控制系统受到转矩脉动干扰时，电机负载转矩作为被控对象，其实际模型可以用标准模型与实际模型变量的组合来表示。被控对象可表示为

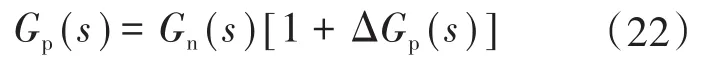
式中：Gn(s)为被控对象标准模型；ΔGp(s)为被控对象实际模型的变化量。

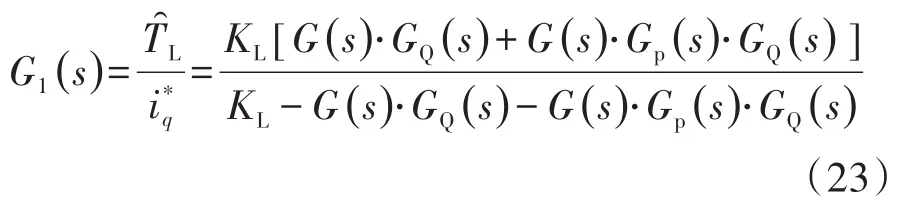
传递函数变化量ΔG1(s)为

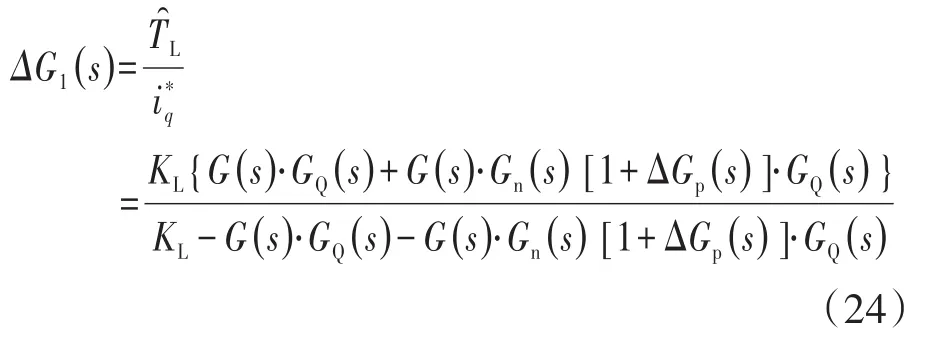
由式（24）可以得到传递函数的灵敏度函数和补灵敏度函数为

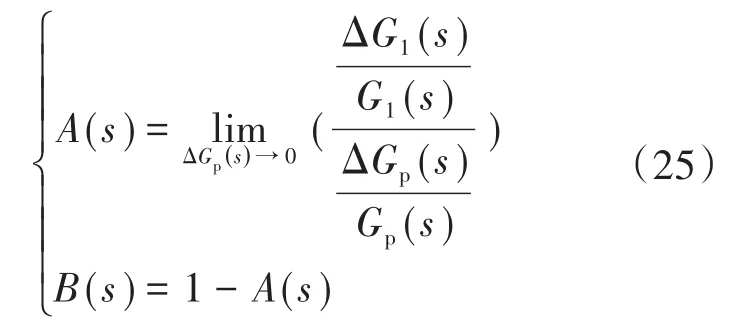
小增益控制理论的稳定性判据充要条件为

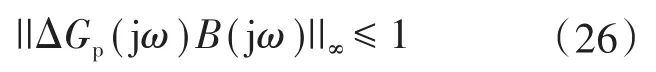
将式（23）～式（25）代入式（26）中，可知满足系统稳定性判据的条件，从而证明了本文所提扰动转矩观测器的稳定性。

4 试验分析

为了验证本文所提改进定子磁链估计器和扰动转矩观测器可以提高PMSM无位置传感器控制性能，搭建了电机试验平台。

试验参数如下：电机功率2.2kW；额定电流8.7A；直轴电感1.241 mH；额定转速3 000 r/min；交轴电感1.245 mH；直流母线电压24 V；极对数2；额定转矩1.5 N·m；定子电阻0.3 Ω；永磁磁通幅值为0.014 3 Wb。

电机驱动单元及控制模块如图4所示。

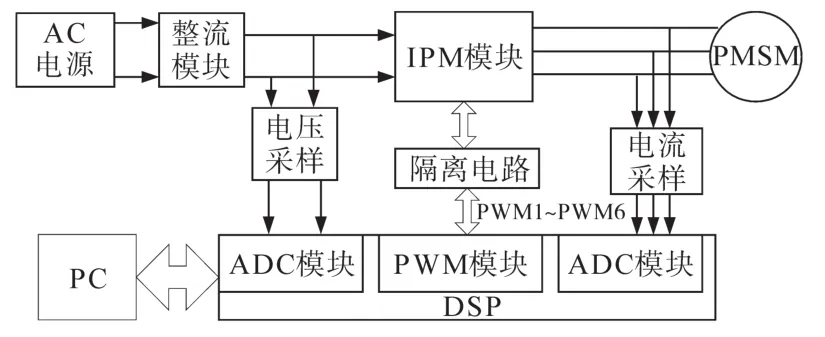
图4 PMSM驱动系统示意图Fig.4 Schematic diagram of PMSM drive system

图4中，驱动单元包括整流电路、IPM驱动模块等；控制模块包括数字信号处理器TMS320F28335、电源电路、保护电路、采样电路、接口电路等。

为了验证本文所提基于低速脉冲高频定子磁链注入法的无位置传感器PMSM控制性能，进行以额定转矩0.22 N·m、额定转速100 r/min的稳态试验。为了方便高频信号提取，在定子磁链中注入500 Hz的正弦电压信号。估计和实际转子位置如图5a所示，估计转速和实际转速波形如图5b所示，估计和实际转子位置误差如图6a所示，估计定子和实际转速误差如图6b所示。

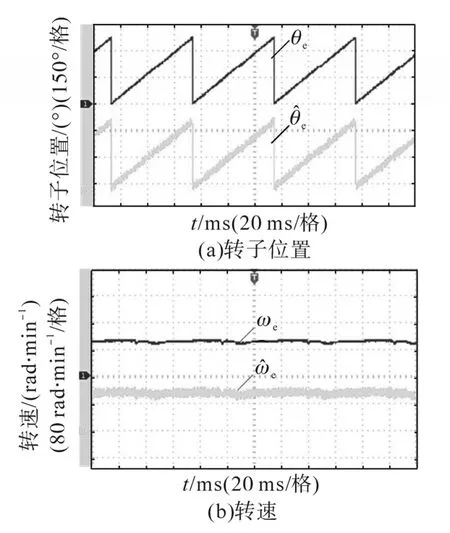
图5 估计和实际转子位置、转速对比图Fig.5 The contrast of estimated and actual rotor position and speed

图6 估计和实际转子位置、转速误差图Fig.6 Error chart of estimated and actual rotor position and speed

由图5a可知：新型磁链估计器估计的转子相角与实际PMSM转子相角相位一致，估计值能很好地跟踪实际值。由图6a可知：估计误差可以控制在±1°之间，相位无滞后。由图5b可知：电机在低转速运行时，估计转速和实际转速均在100 r/min左右，频率与转子磁场的速度相一致，估计转速能够准确跟踪实际转速。由图6b可知：估计转速与实际转速误差小，可以控制在1.5 rad/min之间，实现了低速情况下，PMSM无位置传感器控制。

PMSM相电流波形如图7所示。

图7 PMSM相电流波形Fig.7 PMSM phase current waveform

由图7可知：由于注入信号的幅度很小，相电流仍然是正弦的，电流波形较为光滑，更加接近于正弦波，尖峰毛刺较少，峰-峰值处的波形畸变率较小，输出电能质量较高。为了验证本文所提扰动转矩观测器可以提高无位置传感器PMSM控制性能，当电机稳态运行时，在110 ms时突增0.75 N·m的负载转矩。电机从启动到稳定转速波形如图8所示。

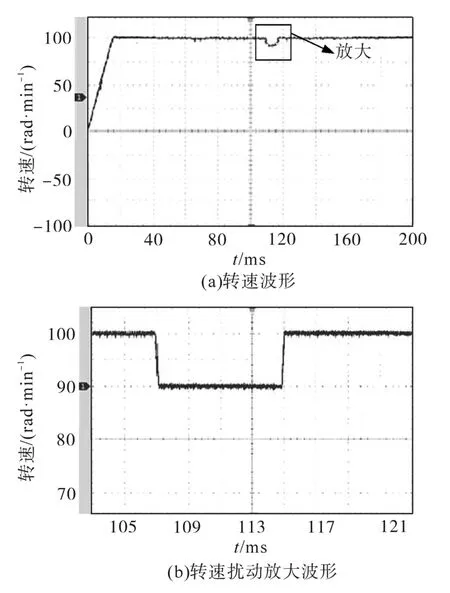
图8 转矩突变PMSM转速波形Fig.8 Waveforms of PMSM speed with torque mutation

由图8a可知：采用本文所提转矩观测器电机从启动到稳定，需要20 ms，超调量极小可忽略不计，转速波形毛刺减少很多，波形较为光滑。由图7b可知：当面对突增0.75 N·m的负载转矩工况时，所提控制方法调节时间为7 ms，转速波动得到有效抑制，系统很快达到稳定状态，且转速无超调，控制效果明显。

5 结论

本文提出了一种基于扰动转矩观测器的PMSM无位置传感器控制系统。对定子磁链估计器进行改进，提高中低速运行时，无位置传感器控制系统转子位置和转速观测精度。针对PMSM中低速运行时，无位置传感器控制系统易受转矩脉动的影响，本文采用扰动转矩观测器来抑制扰动转矩产生的误差。

试验结果表明：本文所提定子磁链估计器可以在电机低转速运行时，有效跟踪实际相位和转速。本文所提转矩观测器灵敏度和准确度较高，可以满足PMSM无位置传感器抗干扰的需要。所提方法具有有效性和较好的实用性，具有一定的理论参考和工程应用价值。